Thermodynamical space-time
• Without interaction, time probably doesn't flow since there is
nothing with respect to which fixing it
(according to some ideas from Ernst Mach [1]).
If the time is connected to interactions, then one may consider an
analogy with statistical thermodynamics (is it the hidden
thermodynamics considered by Louis de Broglie ?) and propound a definition like : 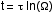 where
where 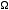 is a number related to the complexity of the Feynman's
diagram describing the studied system, and where
is a number related to the complexity of the Feynman's
diagram describing the studied system, and where  is a
normalization constant (arbitrary ?).
is a
normalization constant (arbitrary ?).
The direction of time evolution [2] would thus be
“evident”
: in order for an event to happen “after” another, it is necessary and
sufficient that it occurs in a diagram of Universe with a greater
number of “branches”. In particular, for an event to be detected before
another, it is necessary that the diagrams describing the second one
would contain more branches
than the diagrams containing some branches describing the interaction
which allows to detect (to “memorize” ?) the first one.
This gives back in particular 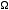 = 1 and t = 0 for
an isolated (bare) propagator, which is consistent with the
relativistic instantaneousness considered here.
= 1 and t = 0 for
an isolated (bare) propagator, which is consistent with the
relativistic instantaneousness considered here.
In the same way, the following diagrams would respectively correspond
to 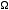 = 4,
= 4, 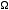 = 3 and
= 3 and 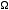 = 6.
= 6.
Dimensionnal analysis elsewhere allows to propound as quantified
elementary time the value
 =
= 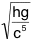 = 1,34.10-43
s (sometimes named “Planck's time”, but it is not necessarily
this value which is convenient).
= 1,34.10-43
s (sometimes named “Planck's time”, but it is not necessarily
this value which is convenient).
• The “time” thus defined a priori corresponds to the one
valid for Universe as a whole. One may therefore conceive to define a
“local” time by restricting the study of connected
diagrams to a (small) part of Universe. It would then remain to resolve
the relativistic problem for two points
“classically” connected by a “space like” interval (the temporal order
of which depends on the framework in special relativity). But in order
to do that, one would before have to specify the notion of motion, and
first of all to specify the notion of distance.
• Within this approach, the time would flow fastly
(?) in the zones of space (?)
where there are more interactions, that is to say very possibly in the
zones where there is more energy for interaction, which leads to a
property qualitatively evoking the relativistic theory of
gravitation.
But some other aspects require reflexion : in
particular the “reduced” crossing
delay occuring in tunnel effect [3]. Some of the particles are
reflected when interacting with the “inaccessible zone”. Those (in
little number) which cross over by tunnel effect seem to go
directly while “insensitive” to the “inaccessible zone”, as if (for
lack of interaction here) this distance
would not exist for them, which (altough little probable) logically
reduces in
consequence the delay of the transit (in the rare cases
when this happens). That could it thus be
considered as a possible consequence of the preceding interpretation of
time ? On the one hand one would have to precise the interpretation, on
the other hand il would be necessary to give confirmation through some
analogous behaviours for other situations
: in an interference apparatus such as Young's splits, the particules
crossing over a “dark fringe” without interacting there do they have
because of that a reduced transit delay ?
• From another point of vue, if one founds upon the analogy between on
the one hand : dU = T dS - p
dV with :
U the internal energy, T the temperature, S the entropy, p
the pressure and V the volume
and one the other hand : dA = E dt - p dx
with :
A the action, E the energy, t the time, p the
momentum and x the position
then the connection of (T,p) with (E,p) suggests that the
energy-momentum of an isolated quantum particle does not exist ; this
would be a mean statistical property of interactions (assuming that
there is
“quasi-equilibrium”, which perhaps corresponds to the mass shell ?).
• In a situation of quasi-equilibrium, the energy and the momentum are
connected by a state equation ;
this one does not apply far from equilibrium. Heisenberg's
uncertainties for the particles “out of their mass shell”
are perhaps only the statistical description of the fluctuations about
the equilibrium (the larger as the deviation from equilibrium is
violent).
• Is it possible to extend the analogy and to consider a quantity
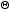 ,
analogous of the thermal transfert (heat), such as d
,
analogous of the thermal transfert (heat), such as d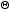 ≤ E
dt in an analogous way as dQ ≤ T dS (with
equality in the cases close from an equilibrium state ?).
≤ E
dt in an analogous way as dQ ≤ T dS (with
equality in the cases close from an equilibrium state ?).
Since in thermodynamics the local entropy creation is proportional to  or
or 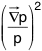 , one may consider here a
local time creation that would be proportional to a term like
, one may consider here a
local time creation that would be proportional to a term like  where it would be still
necessary to transform the “gradient” because this describes a
derivative with respect to the position in space (which “space” ?). Is it
possible to consider for this purpose the ratio of the energy variation
to the local “length of interaction chain” ?
where it would be still
necessary to transform the “gradient” because this describes a
derivative with respect to the position in space (which “space” ?). Is it
possible to consider for this purpose the ratio of the energy variation
to the local “length of interaction chain” ?
• Within a “neighbourhood” of an equilibrium, the analogous or the
energy conservation for a thermodynamical system would be a
quasi-constant action (?). The analogous of a maximum entropy would be
an extremal
time (?).
The analogous of the Boltzmann's factor
e-E/kT
would have to be like 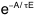 (it would remain to see, from the quantical point of vue, if
there are
variants for the fermions and the bosons). The more probable actions
would therefore be the smallest, and all the more for weak energy. It
is moreover possible that the action would be
quantized (with quantum h).
(it would remain to see, from the quantical point of vue, if
there are
variants for the fermions and the bosons). The more probable actions
would therefore be the smallest, and all the more for weak energy. It
is moreover possible that the action would be
quantized (with quantum h).
• Finally, another analogy could be considered in order to explain the
difference in abundance between matter and
antimatter. Starting from the fact that the integration upon the
energy-momentum of virtual particles (in Feynman's
diagrams) is done including outside the mass shell, and that the same
diagrams can by “turning over”
describe interactions of electrons or positons, one is led to consider
these last as electrons “travelling back in time” [4]. The analogous of
a particule
travelling back in time is an entropy decrease for an isolated system :
although the entropy of such a system would be
statistically inclined to increase, some local fluctuations may happen.
The apparent “time inversions” that the observations of antiparticles
constitute would be unlikely fluctuations, restricted to particular
situations where we detect the effect of the space-time quantization.
__________________
References :
1. “La Mécanique”, E. Mach, ed. J. Gabay (french translation).
2. One may distinguish several notions like the “course of time” which
specifies the direction (apparently ineluctable)
of time
variation and the
“time's arrow” which specifies the direction
of evolution for some irreversible phenomena ; while being in agreement
with the necessity of
clarification suggested by diverse authors, I think that it would be
unreasonable to try to build the notion of time from something else
than its contained events (the time probably does not go if “nothing”
happens, but it remains to know precisely which “nothing”... when it is
usually condidered that a glass is “empty” ever since it does not
contain any liquid) ; that is why I designate also by “time's arrow”
the irreversibility of the “course of time” ; see as example :
“Le temps est différent
des
propriétés qu'on lui attribue”, E. Klein, Science &
Vie, january 2003 ;
“Faut-il distinguer cours du temps et flèche
du temps ?”, E. Klein, Bulletin de l'Union des Professeurs de
Spéciales n° 890, january 2007.
3. see as example (for an interesting interpretation of delays, showing
in particular the absence of light speed overstepping) : “Effet tunnel
: plus vite que la lumière ?”, La Recherche, n° 281,
november 1995.
4. see in particular :
“les intégrales de chemin”, Pour
la Science - les génies de la science, n° 19 (“Feynman,
génie magicien”), may 2004 ;
“la médiation de Dyson”, Pour la
Science - les génies de la science, n° 19 (“Feynman,
génie magicien”), may 2004.
Return to the beginning

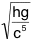 = 1,34.10-43
s (sometimes named “Planck's time”, but it is not necessarily
this value which is convenient).
= 1,34.10-43
s (sometimes named “Planck's time”, but it is not necessarily
this value which is convenient). or
or 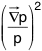 , one may consider here a
local time creation that would be proportional to a term like
, one may consider here a
local time creation that would be proportional to a term like  where it would be still
necessary to transform the “gradient” because this describes a
derivative with respect to the position in space (which “space” ?). Is it
possible to consider for this purpose the ratio of the energy variation
to the local “length of interaction chain” ?
where it would be still
necessary to transform the “gradient” because this describes a
derivative with respect to the position in space (which “space” ?). Is it
possible to consider for this purpose the ratio of the energy variation
to the local “length of interaction chain” ?