Mass and interactions
• An isolated object may not have inertial mass since the principle
of
inertia assumes that the object is affected by the
notion of motion ; then there is no motion concept if there is
nothing
to refer to (according to
Mach's ideas), and if there is some thing, the concerned object is
unable to use it as a reference without interacting with it.
For a massive particle, the proper time between the start and the
arrival is different from zero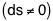 
. This may
suggest that the massive particle does “interact” during its course,
altough if we do not detect those
interactions, more or less like a photon propagating within a
wave-guide
(or through a transparent material), or like an elementary particule
leaving a trace in a bubble chamber. It would then be probably a
very
large amount of infenitesimal interactions (with that is wrongly
called
“vacuum”), and the mass would be a
translation for the mean interaction
energy.
One thus rediscovers the ideas used by renormalized
theories : the “bare” particles are massless and the mass, connected
to
a spontaneous break of symetry, proceeds (in connexion with
renormalization) from dressing of particles by interactions.
Inversely,
for virtual (undetected) particles taking part in Feynman's
diagrams,
one must integrate over all motion
possibilities including outside the “mass shell” [1].
This elsewere introduces some divergences since there exists an
equivalence between the energy-momentum description and the
space-time
description, within which large energies are connected to small
distances. Consequently infinities
do appear when one integrates over large energies, since small
“distances” do not exist as such :
for lack of knowing how to rectify that (what could replace
the integration in question ?), the renormalization used at present
consists to “potter” such diagrams combinations as the divergences
thus
introduced will compensate one another [2].
• However, contrarily to what is generally considered by
renormalized
theories, such interactions might they be limited to
“isolated” virtual interactions ?
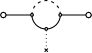
Indeed, in the framework of the preceding investigation, diagrams
not
connected to a significant part of the Univers (such as the first
among
the three ones shown above) may seem to give no inertial effect :
when
a
particule split into a pair of virtual particles, if this pair has
no
interaction with something else, it has no reference able to give
rise
to an inertia
phenomenon.
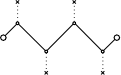
One would then have to consider a multitude of small (“virtual” ?)
interactions with the rest of the Univers (as within the two other
preceding
diagrams, where the propagator ended by
x indicates an “external” unspecified interaction).
Thus, in a manner, there would exist no strictly isolated system (in
the way that what usual quantum theories call “vacuum” is always
present and active). It seems to me that the radiation of an
accelerated electron shows the connexion between inertia and
interaction
(electro-magneto-weak-hard ; I think that there is only one) in the
same way as the behaviour of the Lorentz strength in a change of the
speed shows the connexion between electricity and
magnetism. Mass and inertia are one of the properties of
interactions (and are only that).
• This is not independent from the interpretation that
Feynman had put forward in order to attempt to eliminate within some
calculations the divergences caused by electrons self-interaction
[3] :
when an electron interacts with itself, it “knows that” (through
relativistic instantaneousness, from which Feynman is not far,
altough
he does not mention it in that way, when he considers a “distant”
interaction), and this may not take a part in its inertia
(only the interactions with the other electrons may
contribute to that), therefore not only this may not constitute the
mass origin (self-interaction energy), but this may not so much as
to
contribute to that.
• It may be asked elsewhere whether
“elementary”
(unobserved) interactions, allowed to correspond to the dressing of
a
propagator, are not associated to a kind of
“vibration”
(in a dimension not visible at our scale) as those considered in the
string theories [4].
For the research of such an interpretation, the notion of hidden
“dimensions”
would have to be basically revised since, in the arguments
considered
here, the notion of dimension does not
pre-exist but would be infered from interactions.
• One may finally consider that there would be a connexion between
such
interactions and the large mass of “dark matter” which seems to
miss so as to interpret the motion of stars and
galaxies [5].
• The interpretation must however be careful, because one may also
think that as they modify the number of elementary interactions,
thus
as they modify the notion of time, diagrams such as the second
beside
intervene in the inertia described by the first one.
__________________
References :
1. this may be possibly described by the interaction with the Higgs
boson ; see as example (the
phenomenon is quoted in many articles) : “Qui attrapera le Higgs”,
La
Recherche n° 364,
may 2003.
2. see as example : “Les séries divergentes”, J.P. Ramis, Pour
la Science n° 350, december 2006.
3. see as example (while observing that the “distant” interaction is
not really what its name seems to indicate if the notion of
“distance”
does nos exist at the scale of an elementary interaction) :
“vous voulez rire”, Pour la Science -
les génies de la science, n° 19 (“Feynman, génie
magicien”), may 2004.
4. see as example :
“Le monde
des
cordes est-il le nôtre ?”, P.
Ramond, Pour la Science n° 300, october 2002 ;
“Le paysage
de
la théorie des cordes”, R. Bousso et J. Polchinski, Pour la
Science n° 326, december 2004 ;
while however observing the existence of
difficulties connected to the theories of this kind
(unobserved variations with time for some physical constants) :
“L'Univers avant le
Big Bang”, G. Veneziano, Pour la
Science n° 320, june 2004 ;
“Les constantes... le sont”, C. Pichon, Pour la
Science n° 320, june 2004.
5. see as example (the phenomenon is quoted in many articles) : “La
face cachée des galaxies”, G. Lagache
et
B. Guiderdoni, Pour la Science n° 296, june 2002.
Return to the beginning
