M. X - DYNAMIQUE - INTERACTION DE DEUX POINTS


Mobile relatif et masse réduite

Définitions

• L’interaction dans un système (isolé) de deux points matériels M1M_1 et M2M_2 peut être décrite par :  m1a→1=f→2→1m_1 \; \overset{→}{a}_1=\overset{→}{f}_{2→1}   et   m2a→2=f→1→2m_2 \; \overset{→}{a}_2=\overset{→}{f}_{1→2} .

Le principe des actions réciproques  f→2→1=−f→1→2\overset{→}{f}_{2→1}=-\overset{→}{f}_{1→2}  correspond dans ce cas à la propriété :  m1a→1+m2a→2=(m1+m2)a→G=0→m_1 \; \overset{→}{a}_1+m_2 \; \overset{→}{a}_2=(m_1+m_2 ) \; \overset{→}{a}_G=\overset{→}{0} .  Le référentiel barycentrique est alors galiléen et il est bien approprié pour simplifier les calculs.

◊ remarque : ceci peut se généraliser aux cas où interviennent des forces extérieures, si celles-ci sont en première approximation compensées par les forces d'inertie dans le référentiel barycentrique (non galiléen dans ce cas).

• Dans le référentiel barycentrique :  GM⟶2=−m1m2GM⟶1\displaystyle \overset{⟶}{GM}_2=-\frac{m_1}{m_2} \: \overset{⟶}{GM}_1  donc les positions ne sont pas indépendantes et le problème peut se simplifier.

Puisque la première propriété  ( a→G=0→\overset{→}{a}_G=\overset{→}{0} )  a été déduite d’une combinaison des deux équations du système, une seconde propriété (indépendante) peut être obtenue par une autre combinaison. Il est logique de considérer une combinaison décrivant M1M⟶2\overset{⟶}{M_1 M}_2 :   m1m2.(a→2−a→1)=(m1+m2)f→1→2m_1 \: m_2 .\left(\overset{→}{a}_2-\overset{→}{a}_1 \right)=(m_1+m_2 ) \; \overset{→}{f}_{1→2} .

On appelle alors “masse réduite” la quantité  μ=m1m2m1+m2\displaystyle μ=\frac{m_1 \: m_2}{m_1+m_2}  et on peut nommer “mobile relatif” le point NN tel que  GN⟶=M1M⟶2\overset{⟶}{GN}=\overset{⟶}{M_1 M}_2 ,  auquel on attribue la masse μμ .  L’équation différentielle du mouvement relatif s’écrit ainsi :  μa→N*=f→1→2μ \;\overset{→}{a}{}_N^* =\overset{→}{f}_{1→2}  (en caractérisant par ⬚*⬚^* les quantités calculées dans le référentiel barycentrique).

◊ remarque : on pourrait aussi bien utiliser  GN⟶=M2M⟶1\overset{⟶}{GN}=\overset{⟶}{M_2 M}_1  et  μa→N*=f→2→1μ \;\overset{→}{a}{}_N^* =\overset{→}{f}_{2→1} .

Propriétés

• Le mobile relatif est représentatif de l’énergie cinétique totale Ec*E{}_c^* dans le référentiel barycentrique :
GM⟶1=−μm1GN⟶\displaystyle \overset{⟶}{GM}_1=-\frac{μ}{m_1} \,\overset{⟶}{GN}   et   GM⟶2=μm2GN⟶\displaystyle \overset{⟶}{GM}_2=\frac{μ}{m_2} \,\overset{⟶}{GN}  ;
v→1*=−μm1v→N*\displaystyle \overset{→}{v}{}_1^* =-\frac{μ}{m_1} \, \overset{→}{v}{}_N^*   et   v→2*=μm2v→N*\displaystyle \overset{→}{v}{}_2^* =\frac{μ}{m_2} \, \overset{→}{v}{}_N^*  ;
ainsi :  Ec*=12m1v→1*2+12m2v→2*2=12μv→N*2E{}_c^* =\frac{1}{2} m_1 \; \overset{→}{v}{}_1^{*2}+\frac{1}{2} m_2 \; \overset{→}{v}{}_2^{*2}=\frac{1}{2} μ \; \overset{→}{v}{}_N^{*2} .

• Le mobile relatif est représentatif du moment cinétique total  L→G=L→G*\overset{→}{L}_G=\overset{→}{L}{}_G^*  dans le référentiel barycentrique :  L→G=GM⟶1×m1v→1*+GM⟶2×m2v→2*=GN⟶×μv→N*\overset{→}{L}_G=\overset{⟶}{GM}_1 × m_1 \; \overset{→}{v}{}_1^*+\overset{⟶}{GM}_2 × m_2 \; \overset{→}{v}{}_2^* =\overset{⟶}{GN} × μ \;\overset{→}{v}{}_N^* .

• Par contre, le mobile relatif est représentatif du mouvement relatif de M2M_2 par rapport à M1M_1 , ou bien du mouvement de M1M_1 ou M2M_2 par rapport à GG , mais non du mouvement d’ensemble de M1M_1 et M2M_2 (donc de GG ) par rapport à GG :
μv→N*=m2v→2*=−m1v→1*μ \;\overset{→}{v}{}_N^* =m_2 \;\overset{→}{v}{}_2^* =-m_1 \;\overset{→}{v}{}_1^*  (mouvements homothétiques),
mais  :  m1v→1*+m2v→2*=0→m_1 \: \overset{→}{v}{}_1^* +m_2 \: \overset{→}{v}{}_2^* =\overset{→}{0}  dans le référentiel barycentrique  ( p→*=0→\overset{→}{p}{}^* =\overset{→}{0} ).

Énergie potentielle

Énergie potentielle d’interaction

• L’interaction de deux points matériels M1M_1 et M2M_2 peut être décrite par leurs actions réciproques :  f→2→1=−f→1→2\overset{→}{f}_{2→1}=-\overset{→}{f}_{1→2} .

Si la force f→2→1\overset{→}{f}_{2→1} dérive d’une énergie potentielle Ep(M1)E_p (M_1) :  f→2→1=−∇→1Ep(M1) \overset{→}{f}_{2→1}=-\overset{→}{∇}_1E_p (M_1)  où ∇→1\overset{→}{∇}_1 correspond à une dérivation par rapport aux coordonnées de M1M_1 .

Mais pour des points matériels, l’énergie potentielle de M1M_1 dans son interaction avec M2M_2 ne peut dépendre que de la distance  r=M1M2r=M_1 M_2 ,  donc elle dépend aussi de M2M_2 :  Ep=Ep(r)=Ep(M1,M2) E_p=E_p(r)=E_p (M_1 \,,M_2) .

Ainsi :  dEp=∇→1Ep⋅dOM⟶1+∇→2Ep⋅dOM⟶2dE_p=\overset{→}{∇}_1 E_p⋅d\overset{⟶}{OM}_1+\overset{→}{∇}_2 E_p⋅d\overset{⟶}{OM}_2  donc cette énergie potentielle, qui décrit les travaux des deux forces réciproques, est donc l’énergie potentielle d’interaction de l’ensemble des deux points.

En outre :  ∇→2r=M2M⟶1r=−∇→1r\displaystyle \overset{→}{∇}_2 \, r=\frac{\overset{⟶}{M_2 M}_1}{r}=-\overset{→}{∇}_1 \, r ,  donc le principe des actions réciproques est vérifié :  f→1→2=−∇→2Ep=−dEpdr∇→2r=dEpdr∇→1r=−f→2→1\displaystyle \overset{→}{f}_{1→2}=-\overset{→}{∇}_2 E_p=-\frac{dE_p}{dr} \, \overset{→}{∇}_2 \, r=\frac{dE_p}{dr} \, \overset{→}{∇}_1 \, r=-\overset{→}{f}_{2→1} .

Enfin, le mobile relatif est représentatif de l’énergie potentielle d’interaction (par rapport à GG ), car EpE_p ne dépend que de  r=M1M2=GNr=M_1 M_2=GN ,  donc on peut écrire :  dEp=∇→NEp⋅dGN⟶dE_p=\overset{→}{∇}_N E_p⋅d\overset{⟶}{GN} .

“Énergie potentielle radiale”

• Si les forces d’interaction dérivent d’une énergie potentielle  Ep=Ep(r)E_p=E_p (r)  avec  r=M1M2=GNr=M_1 M_2=GN ,  alors l’énergie mécanique  Em=12μv2+EpE_m=\frac{1}{2} μ\: v^2+E_p  (associée à NN dans le référentiel barycentrique) est constante.

Or le point NN a une accélération centrale, avec  L→G=μr2θ˙u→z\overset{→}{L}_G=μ \:r^2 \: \dot{θ} \; \overset{→}{u}_z  constant : mouvement selon la “loi des aires” dans le plan perpendiculaire à u→z\overset{→}{u}_z .

Dans le plan du mouvement :  v2=r˙2+r2θ˙2=r˙2+L2μ2r2\displaystyle v^2=\dot{r}^2+r^2 \: \dot{θ}^2=\dot{r}^2+\frac{L^2}{μ^2 \: r^2}  (avec  L=μr2θ˙L=μ \:r^2 \: \dot{θ} )  et on peut obtenir une expression de rr seul :  Em=12μr˙2+L2μ2r2+Ep(r)\displaystyle E_m=\frac{1}{2} μ \:\dot{r}^2+\frac{L^2}{μ^2 \: r^2}+E_p (r) .

En définissant alors une “énergie potentielle radiale” :  Epr(r)=Ep(r)+L2μ2r2\displaystyle E_{pr} (r)=E_p (r)+\frac{L^2}{μ^2 \: r^2}  (dont le second terme décrit l’effet “centrifuge” associé aux rotations de u→r\overset{→}{u}_r autour de GG ), on obtient finalement :  Em=12μr˙2+Epr(r)E_m=\frac{1}{2} μ \:\dot{r}^2+E_{pr} (r) .

◊ remarque : on obtient ainsi, de façon indirecte, l'expression dans le référentiel tournant autour de GG comme M1M_1 et M2M_2 (et NN ), par rapport auquel il n'y a plus qu'un mouvement radial (la rotation n'étant pas uniforme, le passage direct à ce référentiel est loin d'être évident).

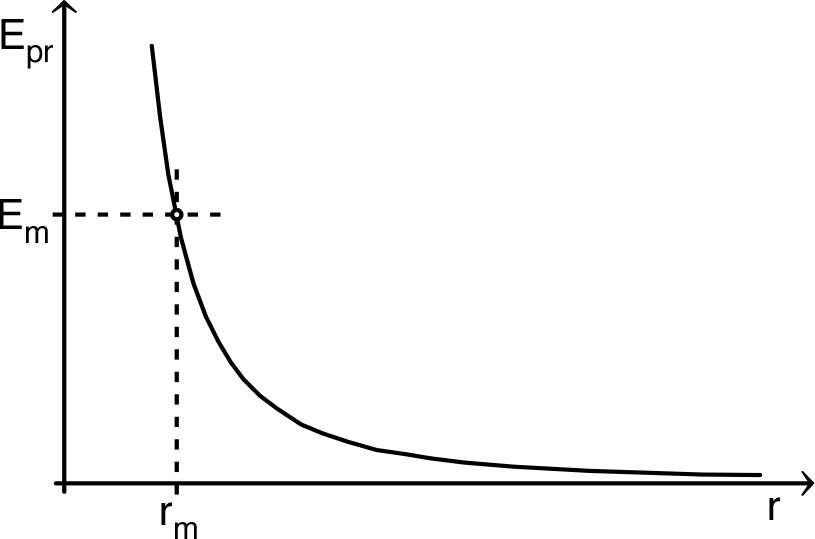
• Si NN était un point isolé (mouvement rectiligne uniforme) :
Em=12μr˙2+L2μ2r2\displaystyle E_m=\frac{1}{2} μ \:\dot{r}^2+\frac{L^2}{μ^2 \: r^2} .

Il y aurait une distance minimale d’approche (de l'origine à la trajectoire pour  r˙=0\dot{r}=0 ) :
rm=L2μEm\displaystyle r_m=\frac{L}{\sqrt{2 \,μ \:E_m}} .
dyn2Points_Im/dyn2Points_Im1.jpg

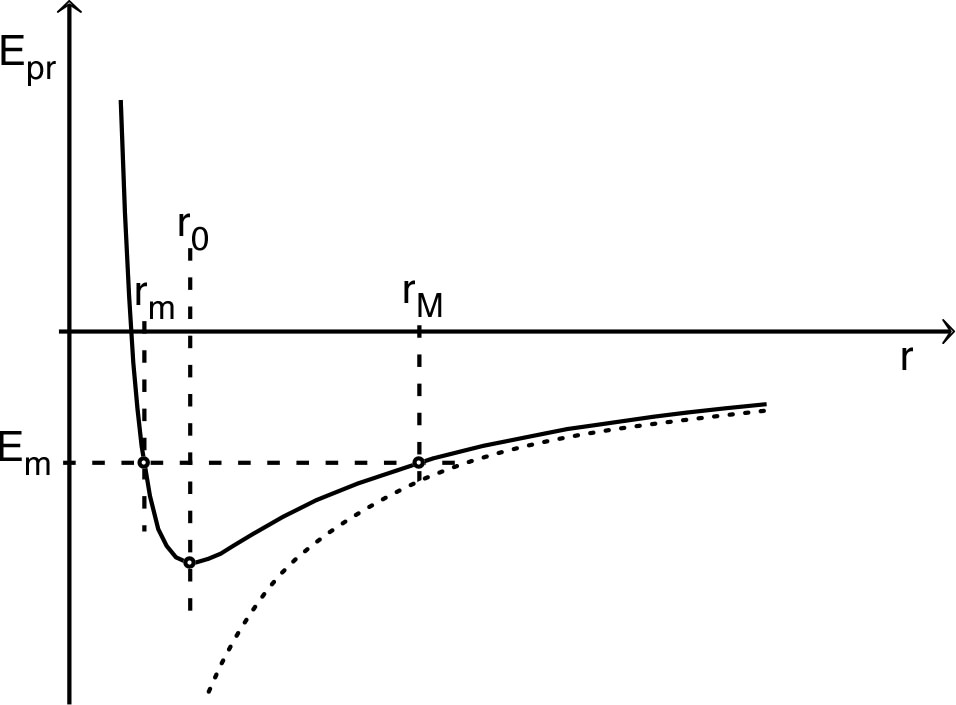
• Pour NN soumis à une force attractive en  −Kr2\displaystyle -\frac{K}{r^2}  et dont le moment cinétique est non nul, on obtient :  Em=12μr˙2−Kr+L2μ2r2\displaystyle E_m=\frac{1}{2} μ \:\dot{r}^2-\frac{K}{r}+\frac{L^2}{μ^2 \: r^2}  d’où on déduit l’existence de mouvements “confinés” (pour  Em<0E_m<0 )  avec une distance minimale rmr_m et une distance maximale rMr_M :

dyn2Points_Im/dyn2Points_Im2.jpg

◊ remarque : à grande distance le terme en  −Kr\displaystyle -\frac{K}{r}  prédomine (pointillé) ; à courte distance l'effet “centrifuge” s'y ajoute.

• Le cas particulier du mouvement circulaire de rayon  r0=L2Kμ\displaystyle r_0=\frac{L^2}{K \:μ}  correspond à l'équilibre relatif, dans le référentiel tournant, avec  dEprdr=0\displaystyle \frac{dE_{pr}}{dr}=0 .

◊ remarque : l'énergie mécanique donnant une expression pour r˙\dot{r} et le moment cinétique en donnant une pour θ˙\dot{θ} , il est toujours possible d'en déduire (au moins numériquement, car ces intégrales sont rarement simples) :

Mouvements des satellites

• On prend l’origine au centre d’inertie GG pour étudier le mouvement de M1M_1 et M2M_2 au moyen d’un “mobile relatif” NN et on considère l’interaction :
f→G→N=f→1→2=−𝒢Mmr2u→r=−𝒢(M+m)mr2u→r=μa→N*\displaystyle \overset{→}{f}_{G→N}=\overset{→}{f}_{1→2}=-𝒢 \,\frac{M \:m}{r^2} \, \overset{→}{u}_r=-𝒢 \,\frac{(M+m) \: m}{r^2} \, \overset{→}{u}_r=μ \;\overset{→}{a}{}_N^* .

Étudiés par rapport à GG , les mouvements ont donc la même forme que celle donnée par l'approximation du corps attracteur très massif : il suffit de remplacer  M→M+mM→M+m  et  m→μm→μ  pour obtenir le mouvement de NN , puis les mouvements de M1M_1 et M2M_2 s'en déduisent par homothétie.

En particulier la troisième loi de Kepler s'écrit ici :  𝒶3T2=𝒢.(M+m)4π2\displaystyle \frac{𝒶^3}{T^2} =\frac{𝒢 .(M+m)}{4 \,π^2} .
📖 exercice n° I.

Notions élémentaires sur les chocs

• Dans le cas général on ne connaît pas la loi de force d’interaction, mais on peut la négliger à grande distance ; on peut se limiter à relier les limites “longtemps avant” et “longtemps après” le choc (en comparaison  de sa durée).

En particulier, pour un système isolé, il y a toujours conservation de la quantité de mouvement totale :  p→1+p→2=p→1′+p→2′\overset{→}{p}_1+\overset{→}{p}_2=\overset{→}{p}{}'_1+\overset{→}{p}{}'_2  (où les “primes” désignent ici les quantités après le choc, dans le même référentiel).

La conservation de l’énergie totale peut aussi être utilisée ; en particulier pour les chocs “élastiques” (où aucune partie du système ne change d’énergie “interne”) il y a conservation de l'énergie cinétique :  Ec1+Ec2=Ec1′+Ec2′E_{c1}+E_{c2}=E'_{c1}+E'_{c2} .

◊ remarque : les chocs inélastiques peuvent être étudiés “plus facilement” en mécanique relativiste, dans la mesure où les modifications “internes” des particules peuvent être décrites par des énergies potentielles d'interaction incluses dans les énergies de masse au repos (la variation des énergies de masse donne la variation des énergies cinétiques).

• Ces deux lois ne permettent pas de déterminer complètement le mouvement limite après le choc (il dépend du moment cinétique total et de la loi de force d’interaction) ; en particulier elles ne donnent pas la répartition angulaire de  θ=(p→1;p→1′)^θ=\widehat{\left(\overset{→}{p}_1;\overset{→}{p}{}'_1 \right)} .