POUSSÉE D'ARCHIMÈDE - corrigé du TP

Étude statique

Dispositif

•.

Mesures

•.

Interprétation

•.

Étude dynamique

Dispositif

• La première expérience utilise une balle de masse

\; m=46\text{,}5 \:\mathrm{g} \;

et de rayon

\; r=21\text{,}35 \:\mathrm{mm} \;

en mouvement dans un tube de hauteur

25 \:\mathrm{cm}

et de diamètre

10 \:\mathrm{cm}

.

La deuxième expérience utilise une balle de masse

\; m=42\text{,}5 \:\mathrm{g} \;

et de rayon

\; r=21\text{,}25 \:\mathrm{mm} \;

en mouvement dans un tube de hauteur

30 \:\mathrm{cm}

et de diamètre

30 \:\mathrm{cm}

.

La troisième expérience utilise une balle de masse

\; m=46\text{,}0 \:\mathrm{g} \;

et de rayon

\; r=21\text{,}30 \:\mathrm{mm} \;

en mouvement dans un tube de hauteur

30 \:\mathrm{cm}

et de diamètre

30 \:\mathrm{cm}

.

• La webcam enregistre

30

images par seconde en

\; 640 × 480 \;

pixels .

Mesures

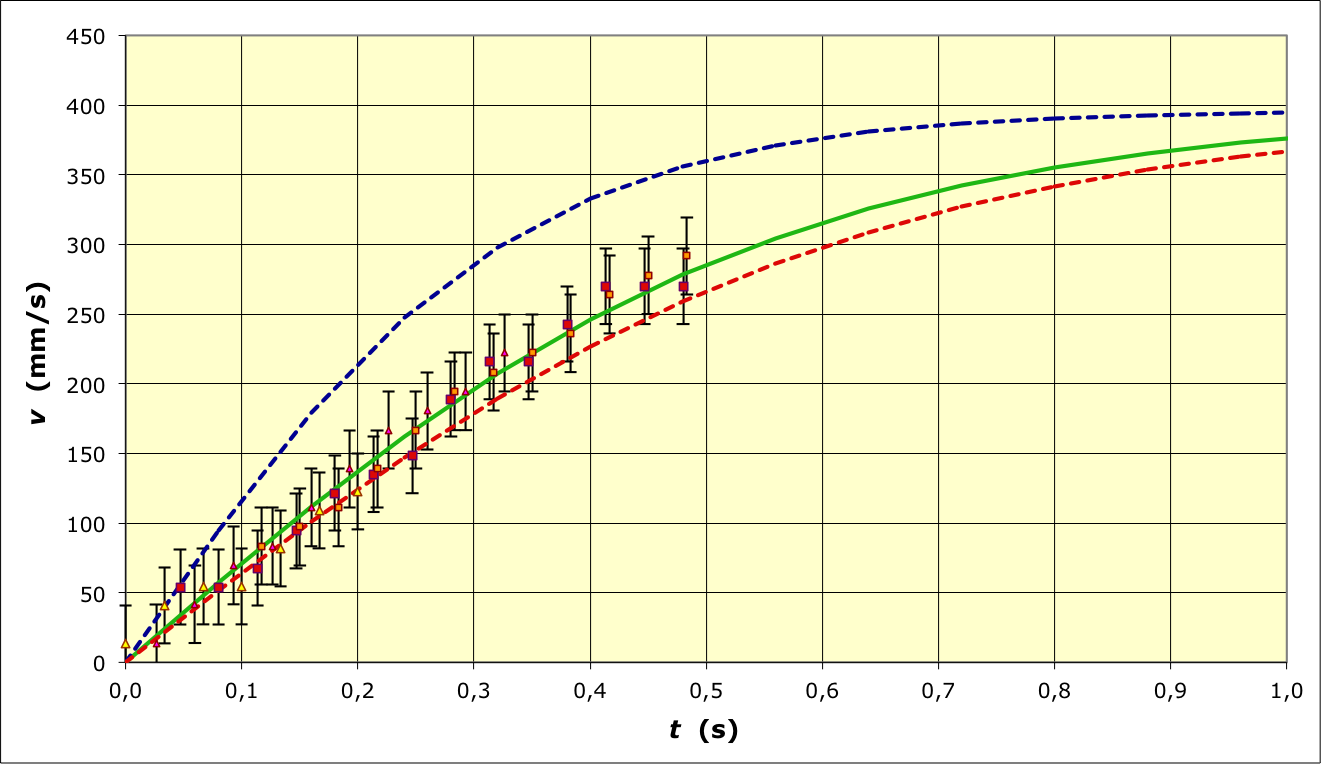
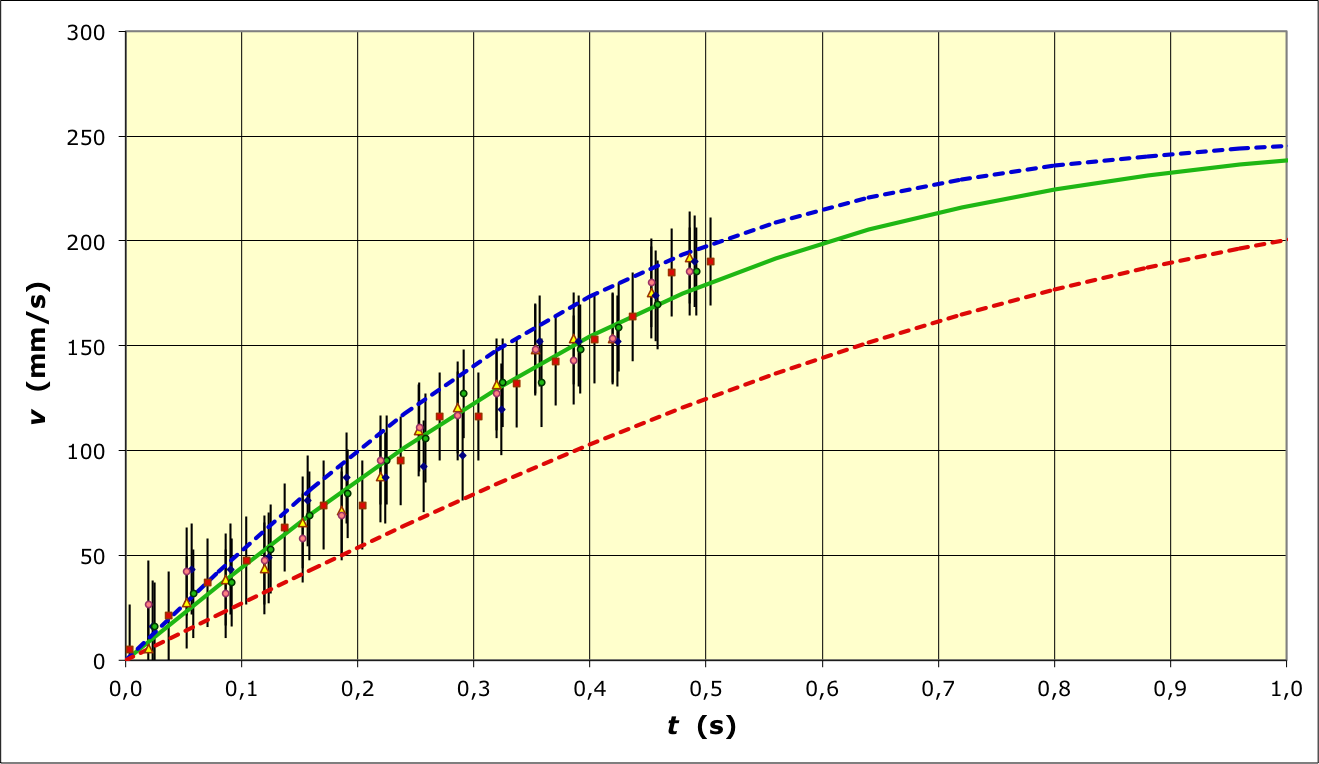
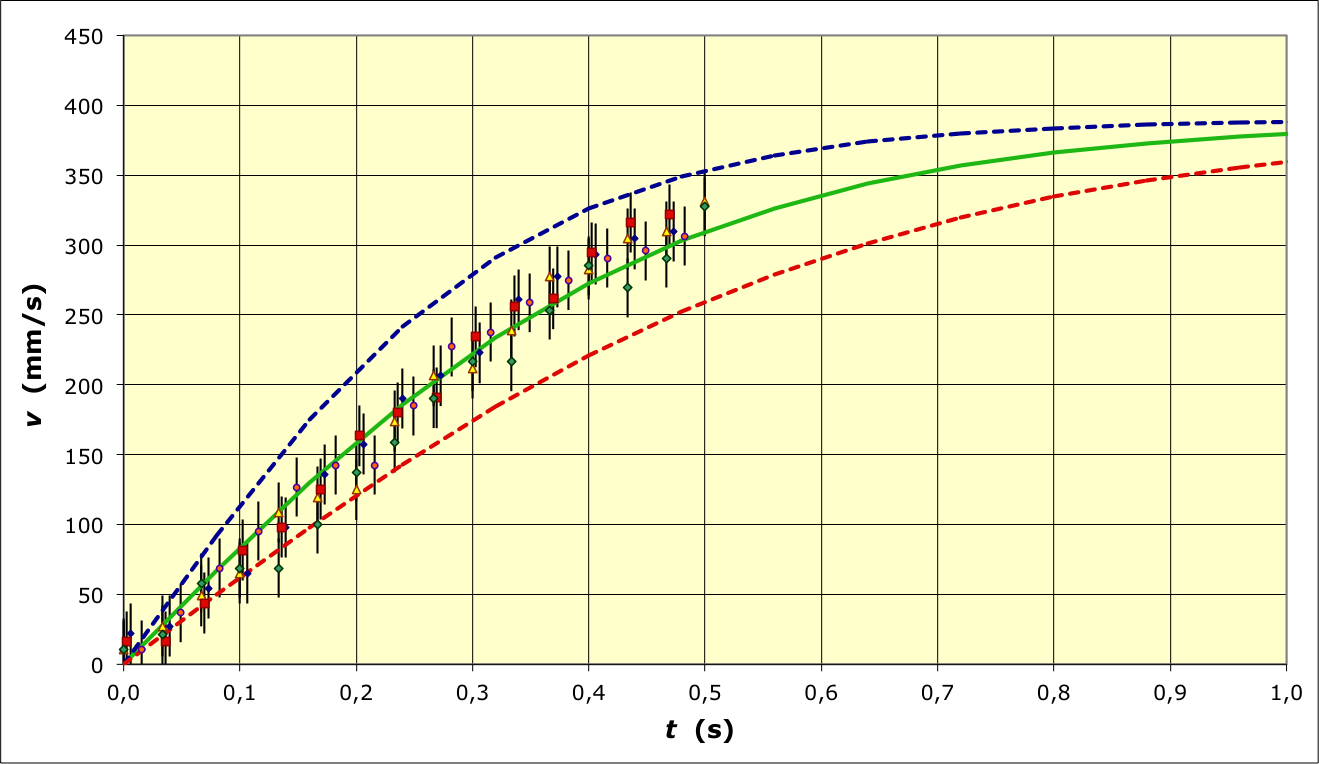
• On obtient les courbes ci-après (les limites correspondant à

\; β=0 \;

\; β=1\;

sont indiquées en pointillés respectivement bleus et rouges).

• Les ajustements donnent tous

\; C_x≈0\text{,}43 \;

\; 0\text{,}45 \;

; ceci correspond aux valeurs généralement admises pour une sphère.

Interprétation

Étude des ordres de grandeur

• On considère un exemple de balle de golf plongée dans l'eau :

la masse est $\; m=46\text{,}5 \:\mathrm{g} \;$ et le rayon $\; r=21\text{,}35 \:\mathrm{mm}$ ;
la masse d'eau déplacée est $\; m_d=40\text{,}8 \:\mathrm{g}$ ;
le poids diminué de la poussée d'Archimède est $\; P\text{’}=55\text{,}9 \:\mathrm{mN}$ .

• Le nombre de Reynolds délimite les régimes :

laminaire réversible pour $\; R_e<1 \;$ ;
laminaire non réversible pour $\; 2<R_e<1000 \;$ ;
turbulent pour $\; R_e>2000$ .

• Avec un frottement visqueux :

la viscosité (dynamique) de l'eau est $\; η=0\text{,}001 \:\mathrm{Pa .s}$ ;
le frottement visqueux sur une sphère $\; f=6π \:r \:η \:v$ ;
la vitesse limite (pour une sphère) serait $\displaystyle \; v=\frac{P\text{’}}{6π \:r \:η}≈140 \:\mathrm{m .s^{-1}}$ ;
le nombre de Reynolds serait $\displaystyle \; R_e=\frac{ρ \:r \:v}{η}≈2.{10}^6≫2000$ ; cela serait nettement contradictoire.

• Avec un frottement turbulent :

le frottement turbulent sur une sphère $\; f=\frac{1}{2} C_x \: S \:ρ \:v^2 \;$ avec $\; C_x≈0\text{,}5$ ;
la vitesse limite (pour une sphère) serait $\displaystyle \; v=\sqrt{\frac{2 \,P\text{’}}{C_x \: S \:ρ}}≈0\text{,}56 \:\mathrm{m .s^{-1}}$ ;
le nombre de Reynolds serait $\displaystyle \; R_e=\frac{ρ \:r \:v}{η}≈12000>2000$ ; cela est plausible.

Modélisation théorique

• Les ordres de grandeur montrent qu'aux grandes vitesses il faut considérer un frottement turbulent, mais le mouvement commence à vitesse nulle, donc au début faible, donc avec un frottement laminaire (visqueux). Une étude des propriétés respectives est nécessaire pour concilier les deux.

• Avec un axe vertical

(Oz)

orienté vers le bas, en notant

m_d

la masse d'eau “déplacée” intervenant dans la poussée d'Archimède (statique) et

m_e=β \:m_d

la masse d'eau “entraînée” intervenant dans la poussée “dynamique”, le frottement visqueux donne l'équation :

(m+m_e) \:\dot{v}=(m-m_d) \:g-λ_1 \: v

avec

λ_1=6π \:r \:η

.

L'intégration donne pour la vitesse :

v(t)=v_1 .\left(1-\mathrm{e}^{-α_1 \: t\,}\right)

avec

\displaystyle v_1=\frac{(m-m_d) \:g}{λ_1}

\displaystyle α_1=\frac{λ_1}{m+β \:m_d}

.

Au début du mouvement :

v(t)≈g\text{’} \:t

(tangente à l'origine) avec une accélération :

\displaystyle g\text{’}=α_1\: v_1=\frac{m-m_d}{m+β \:m_d} \: g

.

• Le frottement turbulent donne l'équation :

(m+m_e) \:\dot{v}=(m-m_d) \:g-λ_2 \: v^2

avec

λ_2=\frac{1}{2} C_x \: S \:ρ

.

L'intégration donne pour la vitesse :

v(t)=v_2 \: \tanh(α_2 \: v_2 \: t)

avec

\displaystyle v_2=\sqrt{\frac{(m-m_d) \:g}{λ_2}}

\displaystyle α_2=\frac{λ_2}{m+β \:m_d}

.

Au début du mouvement :

v(t)≈g\text{’} \:t

(tangente à l'origine) avec une accélération :

\displaystyle g\text{’}=α_2 \: v_2^{\:2}=\frac{m-m_d}{m+β \:m_d} \: g

identique à celle obtenue pour un frottement laminaire.

◊ remarque : on peut aussi envisager une description par l'étude de

v(z)

\displaystyle v \: \frac{dv}{dz}=g\text{’}-α_2 \: v^2

, dont l'intégration donne :

\displaystyle v(z)=v_2 \: \sqrt{1-\mathrm{e}^{-2α_2 z}}

; au début du mouvement :

v^2 (z)≈2 \,g\text{’} \:z

(tangente à l'origine) ; les incertitudes relatives sur

v^2

sont toutefois plus grandes et cette méthode est globalement moins bonne.

• L'analogie des comportements à faible vitesse justifie qu'on puisse utiliser un modèle turbulent même aux plus faibles vitesses (où cela est moins justifié), ce qui permet un traitement global des mesures sans devoir chercher un “raccordement” de deux modélisations.

Commentaires sur les mesures

• Les trois exemples sont globalement bien décrits par la modélisation, mais plutôt déroutants :

le premier donne $\; β≈0\text{,}78±0\text{,}15 \;$ plutôt compatible avec un entraînement d'eau important (cela provient peut-être du tube plus étroit, causant un influence plus grande de la circulation d'eau remontant autour de la balle) ;
le deuxième donne $\; β≈0\text{,}20±0\text{,}15 \;$ plutôt compatible avec un entraînement d'eau faible (cela peut provenir des faibles vitesses dans un tube plus large) ;
le troisième donne $\; β≈0\text{,}45±0\text{,}10 \;$ tout à fait intermédiaire (pour des plus grandes vitesses dans un tube plus large)...

• Il semble donc que l'étude dynamique de la balle en interaction avec l'eau nécessite une approche plus détaillée de mécanique des fluides (non envisagée ici, faute de temps...).

◊ remarque : si d'aucuns ont des idées pour améliorer simplement l'expérimentation (sans nécessiter de dispositif trop élaboré), les suggestions sont bienvenues...