Énergie potentielle d'interaction des anneaux magnétiques


Interaction de deux aimants alignés

• Pour un aimant de moment magnétique ℳ→1\overset{→}{ℳ}_1 , le champ magnétique est : B→1=μ04π(3ℳ→1⋅u→r)u→r−ℳ→1r3\displaystyle \; \overset{→}{B}_1=\frac{μ_0}{4π} \, \frac{(3 \,\overset{→}{ℳ}_1⋅\overset{→}{u}_r ) \: \overset{→}{u}_r- \overset{→}{ℳ}_1}{r^3} \;  donc dans l'axe de l'aimant : B→1=μ02πℳ→1r3 \displaystyle \; \overset{→}{B}_1=\frac{μ_0}{2π} \, \frac{\overset{→}{ℳ}_1}{r^3} .

• La force exercée sur un aimant de moment ℳ→2\overset{→}{ℳ}_2 placé dans l'axe (en disposition “antiparallèle”) est : F→=−∇→Ep\; \overset{→}{F}=-\overset{→}{∇}E_p \; avec Ep=−ℳ→2⋅B→1\; E_p=-\overset{→}{ℳ}_2⋅\overset{→}{B}_1 \; c'est-à-dire : Ep=μ02πℳ1ℳ2r3 \displaystyle \; E_p=\frac{μ_0}{2π} \, \frac{ℳ_1 \, ℳ_2}{r^3} .

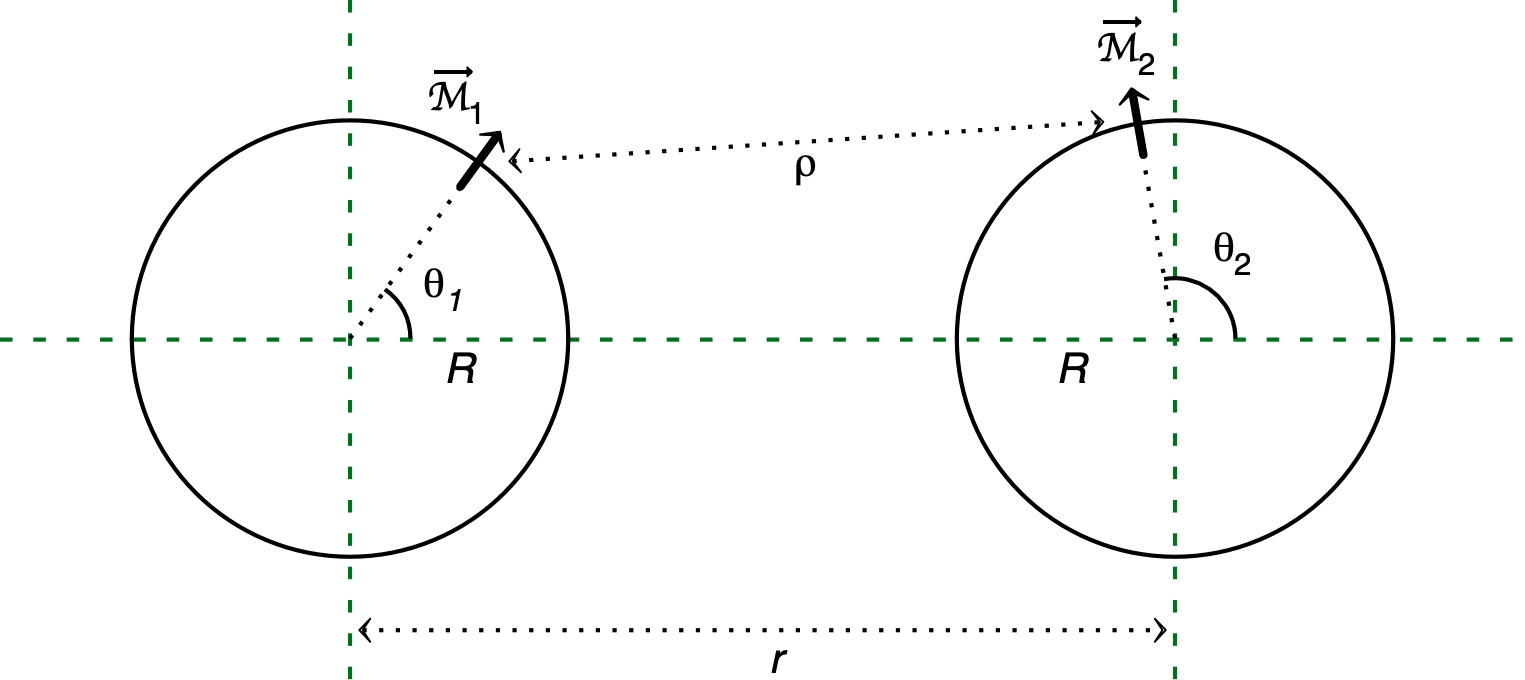
Interaction de deux anneaux entourés d'aimants

• Pour un aimant de moment magnétique ℳ→1\overset{→}{ℳ}_1 , placé dans la direction θ1θ_1 sur le pourtour du premier anneau, en interaction avec un aimant de moment magnétique ℳ→2\overset{→}{ℳ}_2 , placé dans la direction θ2θ_2 sur le pourtour du deuxième anneau, l'énergie potentielle d'interaction est : Ep=−μ02πℳ→1⋅ℳ→2ρ3 \displaystyle \; E_p=-\frac{μ_0}{2π} \, \frac{\overset{→}{ℳ}_1⋅\overset{→}{ℳ}_2}{ρ^3} .

Ep_anneaux_Im/Ep_anneaux_Im1.jpg

• Compte tenu de : ρ2=[r+Rcos(θ2)−Rcos(θ1)]2+[Rsin(θ2)−Rsin(θ1)]2  ceci correspond à :
Ep=−μ02πℳ1ℳ2R3cos(θ2−θ1)[(x+cos(θ2)−cos(θ1))2+(sin(θ2)−sin(θ1))2]3/2\displaystyle E_p=-\frac{μ_0}{2π} \, \frac{ℳ_1 \, ℳ_2}{R^3} \: \frac{\cos(θ_2-θ_1)}{\left[\left(x+\cos(θ_2)-\cos(θ_1) \right)^2+\left(\sin(θ_2)-\sin(θ_1) \right)^2 \right]^{3/2}}   avec  x=rR>2 \displaystyle \; x=\frac{r}{R}>2 .

• En notations réduites, l'énergie potentielle d'interaction totale de tous les aimants d'un anneau avec tous ceux de l'autre anneau peut s'écrire sous la forme :
ℰ(x)=∫02π∫02πcos(θ2−θ1)[(x+cos(θ2)−cos(θ1))2+(sin(θ2)−sin(θ1))2]3/2dθ1dθ2\displaystyle ℰ(x)=∫_0^{2π} ∫_0^{2π} \frac{\cos(θ_2-θ_1 )}{\left[\left(x+\cos(θ_2)-\cos(θ_1) \right)^2+\left(\sin(θ_2)-\sin(θ_1) \right)^2 \right]^{3/2}} \; dθ_1 \: dθ_2 .

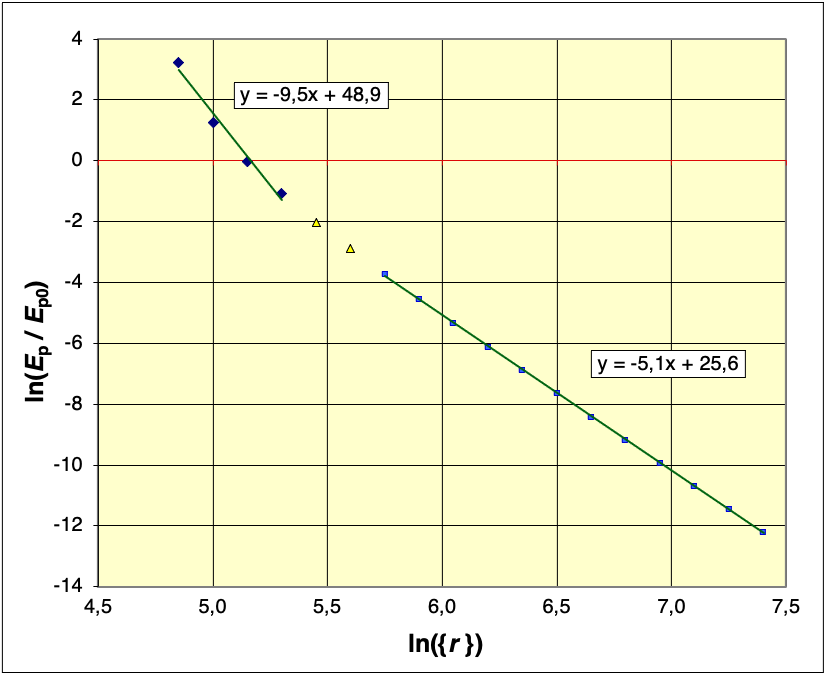
• Le calcul numérique montre graphiquement une dépendance en 1r5\displaystyle \; \frac{1}{r^5} \; à grande distance, mais une variation nettement plus rapide à plus courte distance : exposant entre 77 et 1010 .

Toutefois, cette modélisation ne tient pas compte d'une diminution (probable à faible distance) de l'aimantation des barreaux magnétiques en interaction : au niveau microscopique, le changement de polarisation par influence fait que le champ B→1\overset{→}{B}_1 tend à diminuer le moment dipolaire ℳ→2\overset{→}{ℳ}_2 en opposition (et réciproquement). Cela pourrait donc être compatible avec l'exposant expérimental ≈7≈7 .

Ep_anneaux_calculs/Ep_anneaux.png