Énergie potentielle d'interaction des barreaux magnétiques


Interaction de deux aimants alignés

• Pour un aimant de moment magnétique ℳ→1\overset{→}{ℳ}_1 , le champ magnétique est : B→1=μ04π(3ℳ→1⋅u→r)u→r−ℳ→1r3\displaystyle \; \overset{→}{B}_1=\frac{μ_0}{4π} \, \frac{(3 \,\overset{→}{ℳ}_1⋅\overset{→}{u}_r ) \: \overset{→}{u}_r- \overset{→}{ℳ}_1}{r^3} \;  donc dans l'axe de l'aimant : B→1=μ02πℳ→1r3 \displaystyle \; \overset{→}{B}_1=\frac{μ_0}{2π} \, \frac{\overset{→}{ℳ}_1}{r^3} .

• La force exercée sur un aimant de moment ℳ→2\overset{→}{ℳ}_2 placé dans l'axe (en disposition “antiparallèle”) est : F→=−∇→Epm\; \overset{→}{F}=-\overset{→}{∇}E_{pm} \; avec Epm=−ℳ→2⋅B→1\; E_{pm}=-\overset{→}{ℳ}_2⋅\overset{→}{B}_1 \; c'est-à-dire : Epm=μ02πℳ1ℳ2r3 \displaystyle \; E_{pm}=\frac{μ_0}{2π} \, \frac{ℳ_1 \, ℳ_2}{r^3} .

Interaction de deux aimants sur banc à coussin d'air

• On utilise un banc à coussin d'air préréglé à l'horizontale avec un niveau à bulle, puis ajusté plus précisément avec un palet restant immobile au milieu (c'est plus sensible à la moindre pente).

Les résultats de l'expérience qui suit mettant toutefois en évidence l'existence d'une pente résiduelle, une observation plus détaillée a montré que, suite à l'usage pendant de nombreuses années, le banc n'était plus rectiligne mais “en creux” au milieu. Dans l'impossibilité de recommencer l'expérience faute de créneau horaire disponible, le défaut a été compensé lors de l'exploitation des mesures en prenant en compte l'inclinaison de la partie du banc utilisée.

• On fixe à l'extrémité du banc à coussin d'air un barreau aimanté parallèle au banc ; on fixe sur un palet un autre barreau aimanté identique en opposition.

L'interaction se produisant près d'une extrémité, on peut corriger la courbure indésirable du banc en raisonnant comme pour un banc de pente constante (repérée par un angle αα ).

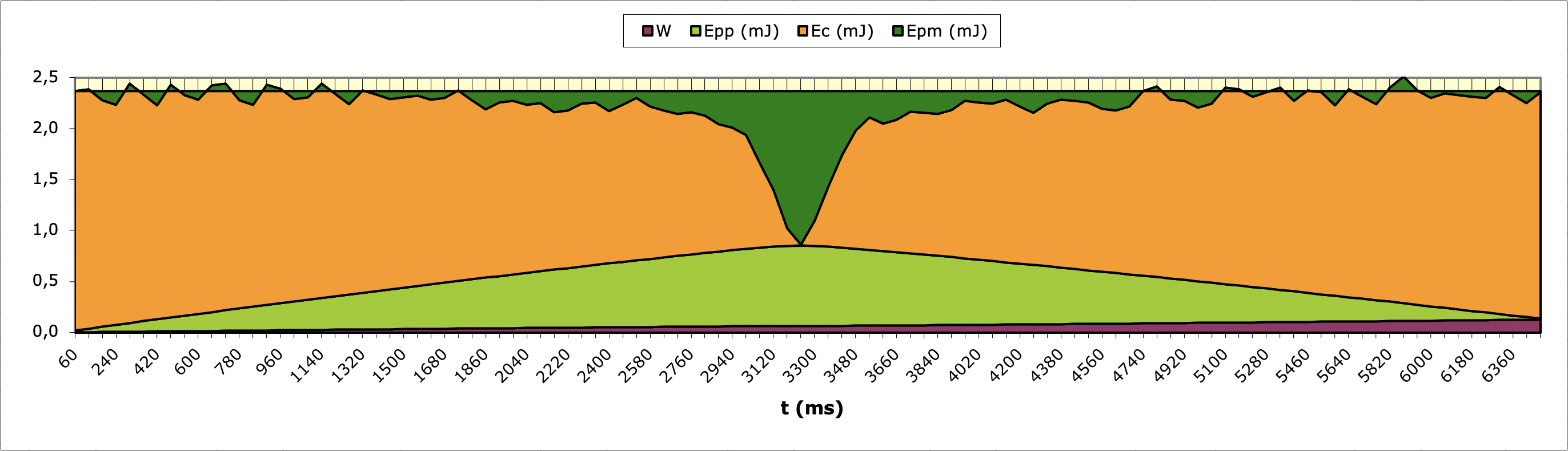
• On lance le palet mobile vers l'aimant fixe et on enregistre le mouvement avec répulsion ; plusieurs essais sont nécessaires pour obtenir l'approche à une distance la plus petite possible (afin que l'énergie magnétique à mesurer soit plus grande) sans provoquer de “choc dur” entre les aimants.

• Bien que le coussin d'air soit efficace, il subsiste des frottements, mais ils sont assez faibles pour qu'il soit assez efficace de les modéliser par un frottement solide (plus simple pour les calculs) : f→=−fu→\; \overset{→}{f}=-f \;\overset{→}{u} \; avec une norme ff constante et u→=v→v\displaystyle \; \overset{→}{u}=\frac{\overset{→}{v}}{v} \; selon le mouvement .

Le travail résistant du frottement est : Wf=−f.(r0−r)\; W_f=-f.(r_0-r) \; à l'aller, puis Wf=−f.(r0+r)\; W_f=-f.(r_0+r) \; au retour.

• En modélisant les barreaux aimantés par des dipôles magnétiques quasi-ponctuels (ils mesurent en réalité ≈3cm≈3 \:\mathrm{cm} ) on exprime un bilan d'énergie en fonction de leur distance rr :
Em−Wf=12mv2+mg.(r0−r)sin(α)+μ02πℳ2r3−Wf=Em0=Cste\displaystyle E_m-W_f=\frac{1}{2} m \:v^2+m \:g .(r_0-r) \; \sin(α)+\frac{μ_0}{2π} \, \frac{ℳ^2}{r^3} -W_f=E_{m0}=Cste .

• L'énergie magnétique est négligeable à grande distance et l'énergie potentielle de pesanteur revenant finalement à sa valeur initiale (qu'on peut choisir Epp0=0 \; E_{pp0}=0 ), on peut ajuster ff pour retrouver la même valeur limite à la fin et au départ (en violet sur le graphique).

EmBanc.png

Cela correspond à f=0,15±0,015mN \; f=0\text{,}15±0\text{,}015 \:\mathrm{mN} .

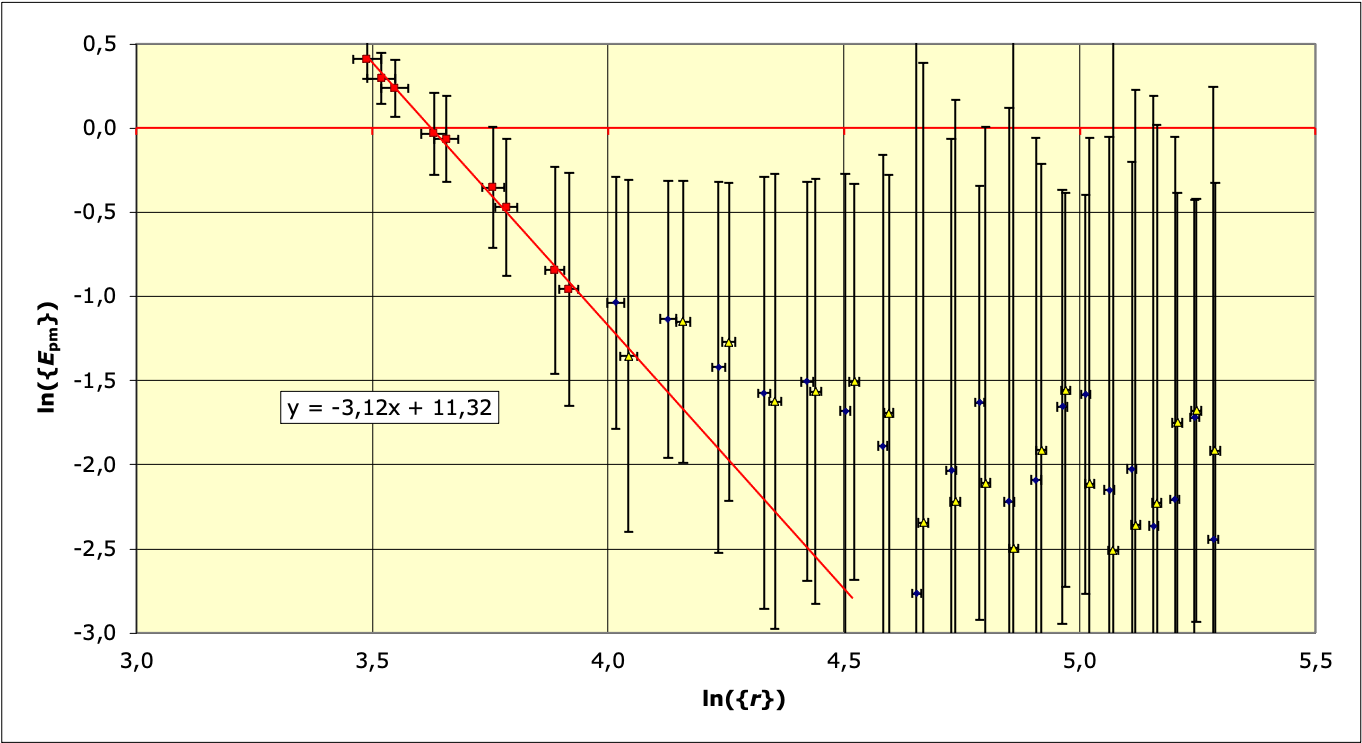
• On peut ensuite ajuster αα et le coefficient K=μ02πℳ2\displaystyle \; K=\frac{μ_0}{2π} \, ℳ^2 \; afin de retrouver à la fois la constante énergétique et la variation de l'énergie potentielle magnétique selon :  ln({Epm})≈ln({K})−3ln({r})\ln(\{E_{pm}\} )≈\ln(\{K\})-3 \; \ln(\{r\}) .

EpmBanc.png

L'ajustement n'est que partiellement démonstratif dans la mesure où les deux constantes sont fortement corrélées : on ajuste la pente de façon à obtenir un comportement le plus linéaire possible pour les points aux faibles valeurs de rr dans le diagramme logarithmique de EpmE_{pm} (là où cette dernière a les plus grandes valeurs).

On obtient : gsin(α)=(9,4±1,9).10−3m.s−2\; g \; \sin(α)=(9\text{,}4±1\text{,}9).{10}^{-3} \: \mathrm{m.s^{-2}} \;  et  K≈8,2.10−8J.m3\; K≈8\text{,}2.{10}^{-8} \: \mathrm{J.m^3} \; (c'est-à-dire ℳ≈0,64A.m2 \; ℳ≈0\text{,}64 \:\mathrm{A.m^2} ),  avec par ailleurs : n=3,1±0,7\; n=3\text{,}1±0\text{,}7 \; en accord avec l'interprétation du modèle proposé.