M. III - DYNAMIQUE ; ÉNERGIE MÉCANIQUE


Théorème de l’énergie cinétique

• Soit MM un point soumis à une force F→\overset{→}{F} , on définit le travail δWδW de cette force lors d’un déplacement dOM⟶d\overset{⟶}{OM} par :  δW=F→⋅dOM⟶=F→⋅v→dtδW=\overset{→}{F}⋅d\overset{⟶}{OM}=\overset{→}{F}⋅\overset{→}{v} \: dt .

Le travail de la force F→\overset{→}{F} pour un déplacement de M1M_1 à M2M_2 est par conséquent :  W12=∫M1M2F→⋅dOM⟶\displaystyle W_{12}=∫_{M_1}^{M_2} \:\:\overset{→}{F}⋅d\overset{⟶}{OM}  (dans le cas général, l’intégrale dépend du trajet suivi).

La puissance fournie au point MM par la force F→\overset{→}{F} est par ailleurs :  𝒫=F→⋅v→𝒫=\overset{→}{F}⋅\overset{→}{v} .

• D’après le principe fondamental :
∑F→i=dp→dt=mdv→dt\displaystyle ∑ \overset{→}{F}_i =\frac{d\overset{→}{p}}{dt}=m \, \frac{d\overset{→}{v}}{dt}    et   ∑δWi=mv→⋅dv→=d(12mv2)=dEc\displaystyle ∑ δW_i=m \:\overset{→}{v}⋅d\overset{→}{v}=d\left(\frac{1}{2} m \:v^2 \right)=dE_c .

La variation de l’énergie cinétique est donc égale à la somme des travaux des forces exercées sur le point MM :  ΔEc=WΔE_c=W .

Énergie potentielle

• Une force F→\overset{→}{F} dérive d’une énergie potentielle (notée EpE_p ) si et seulement s’il existe une fonction Ep(M)E_p (M) telle que :  F→=−∇→Ep\overset{→}{F}=-\overset{→}{∇}E_p  (gradient de EpE_p ),  c'est-à-dire en coordonnées cartésiennes :  Fx=−∂Ep∂x\displaystyle F_x=-\frac{∂E_p}{∂x}  ;  Fy=−∂Ep∂y\displaystyle F_y=-\frac{∂E_p}{∂y}  ;  Fz=−∂Ep∂z\displaystyle F_z=-\frac{∂E_p}{∂z} .

Le travail infinitésimal  dW=F→⋅dOM⟶=−dEpdW=\overset{→}{F}⋅d\overset{⟶}{OM}=-dE_p  donne dans ces conditions une intégrale  W12=∫M1M2F→⋅dOM⟶=−ΔEp\displaystyle W_{12}=∫_{M_1}^{M_2} \:\:\overset{→}{F}⋅d\overset{⟶}{OM}=-ΔE_p  indépendante du trajet suivi pour aller de M1M_1 à M2M_2 (la fonction EpE_p est une “fonction d’état”).

◊ remarque : si le travail W12W_{12} ne dépend que du point de départ et du point d’arrivée, alors le travail sur un trajet fermé est nul.

◊ remarque : compte tenu de la définition, seules les variations de EpE_p interviennent, donc l’énergie potentielle est définie à une constante additive près (dépendant du choix arbitraire de la référence).

• Par exemple, pour une force de pesanteur uniforme :
P→=mg→\overset{→}{P}=m \:\overset{→}{g}   ;   −dEp=dW=mg→⋅dOM⟶=−mgdz-dE_p=dW=m \:\overset{→}{g}⋅d\overset{⟶}{OM}=-m \:g \:dz  ;
donc  Ep(z)=mgz+Ep0E_p (z)=m \:g \:z+E_{p0}  où Ep0E_{p0} est une constante arbitraire.

• De même, pour une force subie par une particule de charge qq soumise à un champ électrostatique  ℰ→=ℰu→x\overset{→}{ℰ}=ℰ \;\overset{→}{u}_x  uniforme :
F→=qℰ→\overset{→}{F}=q \:\overset{→}{ℰ}   ;   −dEp=dW=qℰ→⋅dOM⟶=qℰdx-dE_p=dW=q \:\overset{→}{ℰ}⋅d\overset{⟶}{OM}=q \:ℰ \:dx  ;
donc  Ep(x)=qℰx+Ep0E_p (x)= q \:ℰ \:x+E_{p0}  où Ep0E_{p0} est une constante arbitraire.

Par contre, pour la force électrostatique causée sur qq par une autre charge ponctuelle q’q\text{’} placée en OO :
F→=14πε0qq’r2u→r\displaystyle \overset{→}{F}=\frac{1}{4π \:ε_0} \, \frac{q \:q\text{’}}{r^2} \: \overset{→}{u}_r   ;   −dEp=dW=14πε0qq’r2u→r⋅dOM⟶=14πε0qq’r2dr\displaystyle -dE_p=dW=\frac{1}{4π \:ε_0} \, \frac{q \:q\text{’}}{r^2} \: \overset{→}{u}_r⋅d\overset{⟶}{OM}=\frac{1}{4π \:ε_0} \, \frac{q \:q\text{’}}{r^2} \, dr  ;
donc  Ep(r)=14πε0qq’r+Ep0\displaystyle E_p (r)=\frac{1}{4π \:ε_0} \, \frac{q \:q\text{’}}{r}+E_{p0}  où Ep0E_{p0} est une constante arbitraire.

• Dans le cas d’un ressort disposé entre OO et MM :   
F→=−k.(r−𝓁0)u→r\overset{→}{F}=-k .(r-𝓁_0 ) \; \overset{→}{u}_r  ;
−dEp=dW=−k.(r−𝓁0)u→r⋅dOM⟶=−k.(r−𝓁0)dr-dE_p=dW=-k .(r-𝓁_0 ) \; \overset{→}{u}_r⋅d\overset{⟶}{OM}=-k .(r-𝓁_0 ) \; dr  ;
donc :  Ep(r)=12k.(r−𝓁0)2+Ep0E_p (r)=\frac{1}{2} k .(r-𝓁_0 )^2+E_{p0}  où Ep0E_{p0} est une constante arbitraire.

• Les forces de frottement ne dérivent pas d’une énergie potentielle puisque le travail des frottements sur un trajet fermé est non nul. Ce travail est toujours résistant, par exemple :  f→=−kv→\overset{→}{f}=-k \:\overset{→}{v}   ;   δW=−kv→⋅dOM⟶=−kv2dt≤0δW=-k \:\overset{→}{v}⋅d\overset{⟶}{OM}=-k \:v^2 \: dt ≤0 .

◊ remarque : on dit que ces forces sont “dissipatives” d'énergie mécanique ; l'étude énergétique complète nécessite alors de prendre en compte l’énergie thermique.

◊ remarque : pour la réaction normale R→\overset{→}{R} au contact d'un solide, le travail est nul :  dW=R→⋅dOM⟶=0dW=\overset{→}{R}⋅d\overset{⟶}{OM}=0  ;  mais on ne peut pas écrire :  “ −dEp=dW=0-dE_p=dW=0 ”  puis  “ Ep=Ep0E_p=E_{p0} ”  (constante arbitraire) car  R→≠−∇→Ep0=0→\overset{→}{R}≠-\overset{→}{∇}E_{p0}=\overset{→}{0}  (R→\overset{→}{R} ne dérive pas d’une énergie potentielle).

📖 exercices n° I et II.

Théorème de l’énergie mécanique

• Pour un point matériel soumis uniquement à des forces dérivant d’une énergie potentielle, on peut poser  Ep=∑Epi\displaystyle E_p=∑ E_{pi}   d’où on déduit le théorème de l’énergie cinétique :  −∆Ep=W=∆Ec-∆E_p=W=∆E_c .

En définissant alors une “énergie mécanique” par  Em=Ec+EpE_m=E_c+E_p ,  la relation précédente s’écrit :  ∆Em=0∆E_m=0  (l’énergie mécanique est constante).

◊ remarque : les forces qui ne font pas varier EmE_m sont dites “conservatives” de l’énergie mécanique :

• Pour un point soumis à :
on peut écrire plus généralement :  −∆Ep=∑Wi=W−∑Wj′=∆Ec−∑Wj′\displaystyle -∆E_p=∑ W_i =W-∑ W{}'_j=∆E_c-∑ W{}'_j  .

Ceci peut s’écrire :  ∆Em=∑Wj′\displaystyle ∆E_m=∑ W{}'_j   (théorème de l’énergie mécanique) où ne sont considérés à droite que les travaux des forces non conservatives de EmE_m .

◊ remarque : le théorème de l’énergie mécanique n’apporte pas d’autre d’information que le théorème de l’énergie cinétique ; il ne fait qu’en donner une autre expression, plus pratique si on connaît l’énergie potentielle.

Application à l’étude des mouvements

• Pour un tir de projectile en l’absence de frottement :  Em=12mv2+mgzE_m=\frac{1}{2} m \:v^2+m \:g \:z   est constante, par suite :  v2=v02−2gzv^2=v_0^{\:2}-2 \,g \:z  ;  cette relation ne résout pas le problème du mouvement (calcul de v(t)v(t) et z(t)z(t) ), mais peut dans certains cas apporter une information utile en évitant des calculs plus compliqués.

• Pour le glissement sans frottement d’un point à la surface d’une sphère :  Em=12mv2+mgzE_m=\frac{1}{2} m \:v^2+m \:g \:z   est constante, mais avec un mouvement plus contraint :  v=rθ˙v=r \:\dot{θ}   et   z=z0+rcos(θ)z=z_0+r \; \cos(θ)  ;  donc :  rθ˙2=2g.[cos(θ0)−cos(θ)]r \:\dot{θ}^2=2\,g .\left[\cos(θ_0 ) - \cos(θ) \right]  (pour un départ avec vitesse nulle), équation qui pourrait donner θ(t)θ(t) .

📖 exercices n° III et IV.

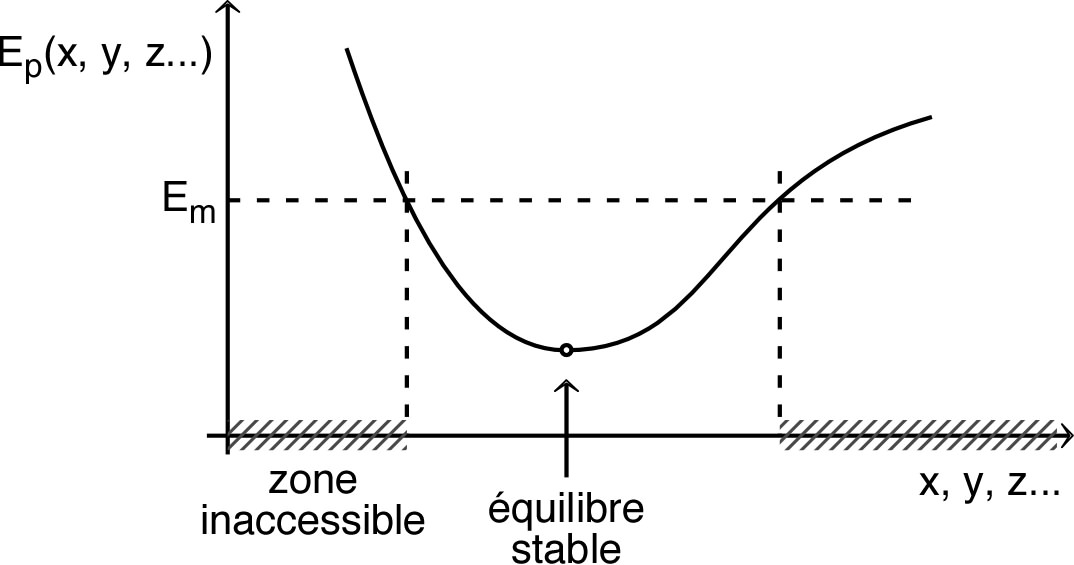
Application à l’étude des équilibres

• Puisque l’énergie cinétique est toujours positive, le point étudié ne peut pas se déplacer dans les régions de l’espace où  Ep(M)>EmE_p (M)>E_m  (“barrière” et “puits” d’énergie potentielle) :

dynEnergie_Im/dynEnergie_Im1.jpg

Dans le cas d’un puits d’énergie potentielle, le point oscille entre des positions extrêmes  (oscillations amorties s’il y a en plus des frottements).

• Le sens de la force  F→=−∇→Ep=−dEpdxu→x\displaystyle \overset{→}{F}=-\overset{→}{∇}E_p=-\frac{dE_p}{dx} \: \overset{→}{u}_x  montre que les équilibres stables correspondent aux minimums relatifs de EpE_p (“force de rappel”) et que les maximums relatifs correspondent à des équilibres instables.

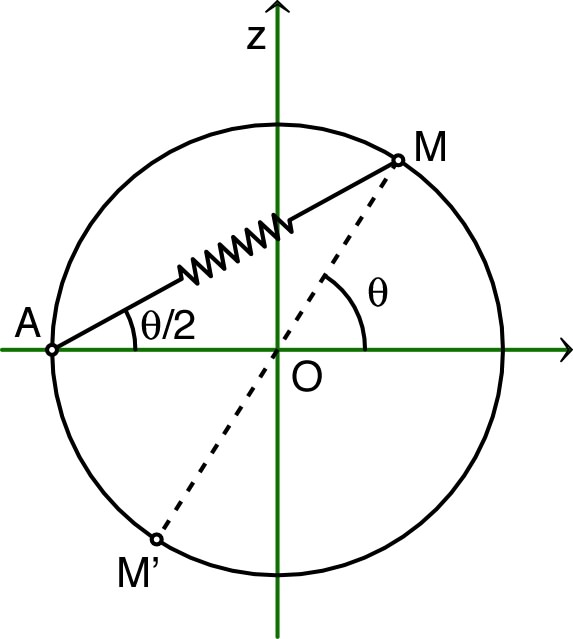
• Soit par exemple un point MM mobile sans frottement sur un cercle de rayon RR , maintenu depuis le point AA par un ressort de masse négligeable, de raideur kk et de longueur “à vide”  𝓁0≪R𝓁_0≪R .

On obtient :  Ep(r)=12k.(𝓁−𝓁0)2+Ep0E_p (r)=\frac{1}{2} k .(𝓁-𝓁_0 )^2+E_{p0}   où  𝓁=2Rcos(θ2)\displaystyle 𝓁=2 \,R \; \cos\left(\frac{θ}{2}\right)   et   z=Rsin(θ)z=R \; \sin(θ)  (la réaction normale a un travail nul, qu’on peut omettre dans le raisonnement basé sur l’énergie).
dynEnergie_Im/dynEnergie_Im2.jpg

• On peut dans ce cas décrire la position avec la variable θθ car le déplacement d'une longueur d'arc  dL=RdθdL=R \:dθ  est simplement proportionnel à dθdθ (cela ne change ni le signe, ni l'annulation des dérivées).

• L’équilibre impose EpE_p extremum :
dEpdθ=−k.(𝓁−𝓁0)Rsin(θ2)+mgRcos(θ)=0\displaystyle \frac{dE_p}{dθ}=-k .(𝓁-𝓁_0 ) \: R \;\sin\left(\frac{θ}{2}\right)+m \:g \:R \; \cos(θ)=0 .

Cette équation se simplifie si  𝓁≈R≫𝓁0𝓁≈R≫𝓁_0 :
𝓁sin(θ2)=Rsin(θ)\displaystyle𝓁 \:\sin\left(\frac{θ}{2}\right)=R \; \sin(θ)   ;   dEpdθ≈−kR2sin(θ)+mgRcos(θ)=0\displaystyle \frac{dE_p}{dθ}≈-k \:R^2 \: \sin(θ)+m \:g \:R \; \cos(θ)=0  ;
on en déduit les deux points MM et M’M\text{’} tels que :  θe=arctan(mgkR)[modπ]\displaystyle θ_e=\arctan\left(\frac{m \:g}{k \:R}\right) \;\; [\mathrm{mod} \:π] .

• L’équilibre stable impose EpE_p minimum :
d2Epdθ2≈−kR2cos(θe)−mgRsin(θe)>0\displaystyle \frac{d^2 E_p}{{dθ}^2} ≈-k \:R^2 \: \cos(θ_e )-m \:g \:R \; \sin(θ_e )>0 .

Compte tenu de la relation vérifiée à l’équilibre, cette relation correspond à :
((mgkR)2+1)cos(θe)=1cos(θe)<0\displaystyle \left(\left(\frac{m \:g}{k \:R}\right)^2+1\right) \: \cos(θ_e )=\frac{1}{\cos(θ_e )} <0  ;
l’équilibre est donc stable en M’M\text{’} et instable en MM .

◊ remarque : si 𝓁0𝓁_0 n'est pas tout à fait négligeable, un développement à l'ordre le plus bas donne un décalage en  θe′≈θe+𝓁02R(1−cos⁡(θe))|cos⁡(θe)|\displaystyle θ'_e≈θ_e+\frac{𝓁_0}{2 \,R} \: (1-cos⁡(θ_e ) ) \: \left| \, cos⁡(θ_e ) \, \right| .

📖 exercices n° V et VI.