ÉTUDE EXPÉRIMENTALE DES FORCES - TP



Modélisation des forces de frottement

Préparation de l’enregistrement

• Ajuster l’horizontalité de la table à coussin d’air, à l’aide des pieds à vis, en vérifiant l’absence de mouvement d’un palet initialement immobile.

• Préparer une feuille d’enregistrement, ainsi que le “second” palet : utile pour la fermeture du circuit électrique formant les étincelles.

• Mesurer la masse d’un palet avec surcharge (celle-ci sert à augmenter le frottement pour mieux l’étudier), puis le lancer (en mouvement “rectiligne uniforme” à la surface de la table), et enregistrer son mouvement.

◊ remarque : la précision relative des mesures nécessite de considérer des intervalles qui ne soient pas trop longs (trop peu de mesures) mais qui ne soient pas trop courts ( l’incertitude sur la position des étincelles est de l’ordre de 0,5mm0\text{,}5 \:\mathrm{mm} ) : ajuster le dispositif à étincelles et la vitesse du palet pour que les intervalles soient de l’ordre de 15mm15 \:\mathrm{mm} .

• Vérifier que la trajectoire est effectivement rectiligne et que le mouvement est en première approximation uniforme. Vérifier qu’en seconde approximation on observe un léger ralentissement progressif.

Le but de l’étude qui suit est de modéliser ce frottement en supposant qu’il s’agit soit d’un frottement “fluide” sur l’air, soit d’un frottement “solide” sur les irrégularités de la surface de la table (le coussin d’air et la surface ne sont pas parfaits).

Modèle du frottement fluide (visqueux)

• Pour les faibles vitesses (si on peut négliger les “tourbillons”), le frottement fluide est dû à la viscosité (celle de l’air est très faible, mais non nulle). Ce frottement est alors proportionnel à la vitesse :  f→=−kv→\; \overset{→}{f}=-k \:\overset{→}{v} \; avec une constante k>0k>0 .

Pour l’étude du mouvement rectiligne, on peut raisonner algébriquement : f¯=−kv¯\; \widebar{f}=-k \:\widebar{v} \; ;  montrer que (compte tenu de la compensation du poids par la réaction normale de la table) la relation fondamentale de la dynamique de translation conduit à : v=v0e−kt/m\: v=v_0 \: \mathrm{e}^{-kt/m} .

Pour se ramener à une variation linéaire, on pourrait considérer  ln(vv0)=−kmt\displaystyle \ln\left(\frac{v}{v_0}\right)=-\frac{k}{m} \,t ,  mais la référence à une vitesse expérimentale initiale v0v_0 augmente les incertitudes. Il est préférable de considérer une valeur de v0v_0 ajustée pour la modélisation. On raisonne pour cela sur les valeurs numériques  {v}=v[v]\displaystyle \{v\}=\frac{v}{[v]}  des vitesses, en simplifiant les unités, ce qui correspond à :  ln({v})=ln({v0})−kmt\displaystyle \ln(\{v\})=\ln(\{v_0\})-\frac{k}{m} \,t  (où {v0}\{v_0\} est une valeur ajustée).

Calculer, puis représenter graphiquement ln({v})\ln(\{v\}) en fonction de tt ; en déduire la valeur de kk permettant de modéliser l’expérience par un frottement fluide ; conclure du point de vue de la précision de ce modèle.

• Dans la mesure où le frottement est faible, on peut utiliser un développement limité : v≈v0.(1−kmt)\displaystyle \; v≈v_0 .\left(1-\frac{k}{m} \, t\right) .  Calculer, puis représenter graphiquement vv en fonction de tt ; en déduire la valeur de kk ; conclure du point de vue de la précision du modèle.

◊ remarque : pour les plus grandes vitesses, le frottement fluide est surtout lié à l’énergie cinétique dissipée dans les tourbillons ; ce frottement est alors proportionnel au carré de la vitesse : f→=−kvv→\; \overset{→}{f}=-k \:v \:\overset{→}{v} \; avec une (autre) constante k>0 \; k>0 .

Modèle du frottement solide

• Le frottement solide est dû au contact des aspérités microscopiques des surfaces. Pour les cas où il y a glissement, il est ici à peu près de norme ff constante (proportionnelle à la réaction normale) : f→=−fu→\; \overset{→}{f}=-f \:\overset{→}{u} \; où u→=v→v\displaystyle \; \overset{→}{u}=\frac{\overset{→}{v}}{v} \; est un vecteur unitaire orienté selon le mouvement.

• Pour l’étude du mouvement rectiligne, on peut raisonner algébriquement ; montrer que la relation fondamentale de la dynamique de translation conduit à : v=v0−fmt \displaystyle \; v=v_0-\frac{f}{m} \, t .

Calculer, puis représenter graphiquement vv en fonction de tt ; en déduire la valeur de ff permettant de modéliser l’expérience par un frottement solide ; conclure du point de vue de la précision de ce modèle (comparer en particulier au développement limité utilisé pour le modèle de frottement fluide faible).

Modélisation des forces magnétiques

Préparation de l’enregistrement

• Préparer une feuille d’enregistrement. Munir les deux palets des anneaux magnétiques ; mettre en place le “second” palet (fixe) utile pour la fermeture du circuit électrique formant les étincelles.

Mesurer la masse du palet (mobile) avec l’anneau magnétique, puis le lancer selon une trajectoire du type représenté ci-contre, en enregistrant son mouvement.

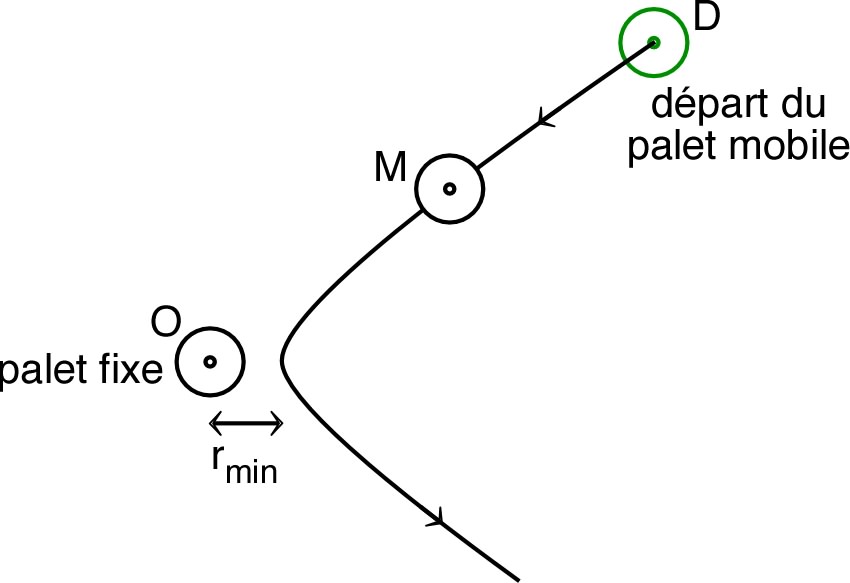
☞ remarque : si on veut obtenir une énergie potentielle magnétique importante pendant le choc (afin de mieux la mesurer) il faut que l'interaction soit grande (passage du palet mobile très proche) ; il peut donc être nécessaire de maintenir le palet fixe (moteur arrêté) pour éviter un effet de recul pendant le choc.
dynEnergie_TP_Im/dynEnergie_TP_Im1.jpg

Modélisation avec une énergie potentielle magnétique

• On suppose que les forces magnétiques entre les deux anneaux dérivent d’une énergie potentielle de la forme : Ep=αrn\displaystyle \; E_p=\frac{α}{r^n} \; avec r=OM\; r=OM \; et des constantes : α>0\; α>0 \; ; n∈N \: n∈N .

• Pour un mouvement curviligne, l’étude complète n’est pas simple, mais on peut raisonner algébriquement avec l’énergie mécanique ; montrer qu’on obtient ainsi : v2+Arn=v02+Ar0n\displaystyle \; v^2+\frac{A}{r^n} =v_0^{\:2}+\frac{A}{r_0^{\:n}} \; et expliciter la constante AA .

Si on suppose l’exposant nn assez grand et r0≫rmin \; r_0≫r_{min} ,  on peut négliger Ar0n\displaystyle \; \frac{A}{r_0^{\:n}} \; en très bonne approximation. En déduire une relation de la forme :  ln({v02−v2})≈ln({A})−nln({r})\ln\left(\{v_0^{\:2}-v^2\}\right)≈\ln(\{A\})-n \;\ln(\{r\}) .

Calculer  ln({v02−v2})\ln\left(\{v_0^{\:2}-v^2\}\right)  et  ln({r})\ln(\{r\})  en fonction de tt , puis représenter graphiquement  ln({v02−v2})\ln\left(\{v_0^{\:2}-v^2\}\right)  en fonction de  ln({r})\ln(\{r\})  ;  en déduire les valeurs de αα et nn permettant de modéliser l’expérience par une énergie potentielle magnétique de la forme considérée ; conclure du point de vue de la précision de ce modèle (conclure en particulier si Ar0n\displaystyle \; \frac{A}{r_0^{\:n}} \; est négligeable et si les frottements sont raisonnablement négligeables).

Prise en compte des frottements

• On suppose que les frottements peuvent être décrits par le frottement solide : f→=−fu→\; \overset{→}{f}=-f \;\overset{→}{u} \; avec une norme ff constante et où u→=v→v\displaystyle \; \overset{→}{u}=\frac{\overset{→}{v}}{v} \; est un vecteur unitaire orienté selon le mouvement. En raisonnant algébriquement avec l’énergie mécanique, montrer qu’on obtient : v2+Arn=v02+Ar0n−CL \displaystyle \; v^2+\frac{A}{r^n} =v_0^{\:2}+\frac{A}{r_0^{\:n}}-C \:L ,  où LL est la longueur (curviligne) parcourue par le palet à partir du point DD et avec une constante C>0 \; C>0 .  Expliciter la constante CC .

Si on suppose l’exposant nn assez grand et r≫rmin \; r≫r_{min} ,  on peut négliger Arn\displaystyle \; \frac{A}{r^n} \; en très bonne approximation. En déduire dans ces conditions une relation “asymptotique” de la forme : v02−v2≈CL \; v_0^{\:2}-v^2≈C \:L .

Calculer LL en fonction de tt , puis représenter graphiquement v02−v2\; v_0^{\:2}-v^2 \; en fonction de LL ; en considérant uniquement les points limites (pour r≫rmin \; r≫r_{min} ,  c’est-à-dire pour L≈0\; L≈0 \; et L≈Lmax \; L≈L_{max} ), en déduire la valeur de ff permettant de modéliser le frottement par un frottement solide ; conclure du point de vue de la précision de ce modèle (conclure en particulier si les frottements sont raisonnablement négligeables).

• Dans le cas général, on peut négliger Ar0n\displaystyle \; \frac{A}{r_0^{\:n}} \; en très bonne approximation, mais il faut tenir compte de Arn\displaystyle \; \frac{A}{r^n} \; pour les points proches de OO .

Calculer  ln({v02−v2−CL})\ln\left(\{v_0^{\:2}-v^2-C \:L\}\right)  en fonction de tt , puis représenter graphiquement  ln({v02−v2−CL})\ln\left(\{v_0^{\:2}-v^2-C \:L\}\right)  en fonction de  ln({r})\ln(\{r\})  ;  en déduire les valeurs de αα et nn permettant de modéliser l’expérience par une énergie potentielle magnétique de la forme considérée ; conclure du point de vue de la précision de ce modèle (conclure en particulier si Ar0n\displaystyle \; \frac{A}{r_0^{\:n}} \; est négligeable).

◊ remarque : les anneaux aimantés sont formés d’une série d’aimants droits pouvant être décrits comme des dipôles magnétiques, caractérisés par un moment ℳ→\overset{→}{ℳ} ; un tel aimant dipolaire crée un champ magnétique B→=μ04π(3ℳ→⋅u→r)u→r−ℳ→r3\displaystyle \; \overset{→}{B}=\frac{μ_0}{4π} \, \frac{(3 \,\overset{→}{ℳ}⋅\overset{→}{u}_r ) \: \overset{→}{u}_r- \overset{→}{ℳ}}{r^3} \,  où μ0≈4π10−7H.m−1\; μ_0≈4π \:{10}^{-7} \: \mathrm{H.m^{-1}} \; est la perméabilité magnétique du vide ; pour deux aimants droits alignés en opposition, on obtient à l'emplacement du second : ℳ→=ℳu→r=−ℳ→′\; \overset{→}{ℳ}=ℳ \:\overset{→}{u}_r=-\overset{→}{ℳ}{}' \; ; B→=μ02πℳ→r3\displaystyle \; \overset{→}{B}=\frac{μ_0}{2π} \, \frac{\overset{→}{ℳ}}{r^3} \;  et  Ep=−ℳ→′⋅B→=μ02πℳ2r3\displaystyle \; E_p=-\overset{→}{ℳ}{}'⋅\overset{→}{B}=\frac{μ_0}{2π} \, \frac{ℳ^2}{r^3} \; ;  ceci correspond à n=3\; n=3 \; ;  pour l’ensemble des anneaux, la situation est plus compliquée, mais on peut raisonnablement envisager une énergie potentielle de forme analogue.




ÉTUDE EXPÉRIMENTALE DES FORCES - TP


Matériel (au bureau)

1 (ou 2) table(s) à coussin d’air avec accessoires        (PRÈS DU TABLEAU)
1 (ou 2) série(s) de 2 anneaux magnétiques
    (masse ≈680g\; ≈680 \:\mathrm{g} \; ou ≈710g\; ≈710 \:\mathrm{g} \; selon la série)
1 rouleau de ruban adhésif
1 balance à lecture directe
1 dynamomètre à ressort sur support
1 boite de masses marquées (avec crochet)
“quelques” feuilles A2 pour enregistrement (× 4 groupes)