DYNAMIQUE - ÉNERGIE - corrigé des exercices



A. EXERCICES DE BASE

Énergie cinétique

1.       • Pendant le choc, quasi-instantané, la vitesse est horizontale donc le poids ne travaille pas ; en outre la vitesse est toujours perpendiculaire à la tension du fil et cette tension ne travaille donc jamais. Au total l’énergie cinétique du point matériel M M reste constante et la norme du vecteur vitesse est conservée.
• Compte tenu de la quasi-instantanéité du choc, on peut considérer que la vitesse reste horizontale (perpendiculaire à la portion extrême du fil), donc le vecteur vitesse est conservé lors du choc.
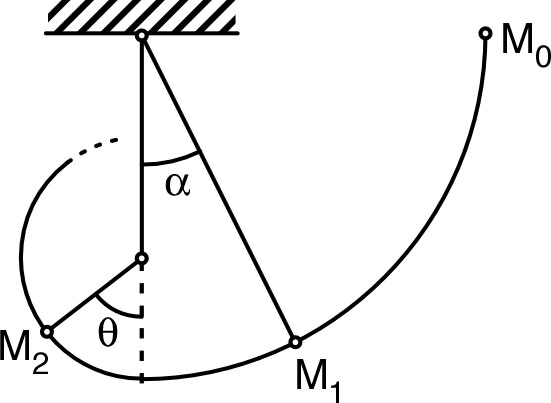
dynEnergie_cor_Im/dynEnergie_cor_Im1.jpg

2.       • Le problème se ramène à celui d’une fronde de longueur L=𝓁−d\;L=𝓁-d\; dont le mobile est lancé dans la position d’équilibre avec une vitesse v0v_0 qui est celle atteinte par MM lors du choc.
◊ remarque : ceci suppose qu’on néglige le “raccourcissement” progressif du fil dû à son enroulement sur une tige de diamètre non nul (on néglige le diamètre de la tige) ; mais le raisonnement ainsi obtenu est correct même si cela change légèrement les coefficients numériques des formules...
• D’après le théorème de l’énergie cinétique entre l’instant initial et l’instant du choc, l’énergie cinétique atteinte est : Ec=12mv02=mg𝓁\;E_c=\frac{1}{2} m \:v_0^{\:2}=m \:g \:𝓁\; ;  par suite : v0=2g𝓁\;v_0=\sqrt{2 \,g \:𝓁\,}\;.
• De même, d’après le théorème de l’énergie cinétique entre l’instant du choc et un instant quelconque précédant le passage au sommet : 12mv2−12mv02=−mg𝓁.[1−cos(θ)]\;\frac{1}{2} m \:v^2-\frac{1}{2} m \:v_0^{\:2}=-m \:g \:𝓁 .\left[1-\cos(θ) \right]\;  et en particulier lors du passage au sommet (s’il est atteint) : 12mv2−12mv02=−2mgL\;\frac{1}{2} m \:v^2-\frac{1}{2} m \:v_0^{\:2}=-2 \,m \:g \:L\; ;  par suite une condition nécessaire pour que le sommet soit atteint est : v2>0\;v^2>0\; et donc : v0>4gL\:v_0>\sqrt{4 \,g \:L}\;.
• En appliquant la relation fondamentale de la dynamique après le choc : ma→=P→+T→\;m \:\overset{→}{a}=\overset{→}{P}+\overset{→}{T}\; et en projetant sur le vecteur u→θ\overset{→}{u}_θ des coordonnées polaires, on obtient : mLθ˙2=mv2L=T−Pcos(θ)\displaystyle \:m \:L \:\dot{θ}^2=\frac{m \:v^2}{L}=T-P \; \cos(θ)\:.  La condition de tension du fil est alors : T=mv2L+mgcos(θ)>0\displaystyle \;T=\frac{m \:v^2}{L}+m \:g \; \cos(θ)>0\; ;  mais compte tenu de la relation de l’énergie cinétique, ceci correspond à : T=mv02L−mg.[2−3cos(θ)]>0\displaystyle \;T=\frac{m \:v_0^{\:2}}{L}-m \:g .[2-3 \:\cos(θ) ]>0\;  quel que soit θ∈[0;π]\;θ∈\left[0 \,;π\right]\;.  En particulier pour le cas limite, il faut : mv02L−5mg>0\displaystyle \;\frac{m v_0^{\:2}}{L}-5 \,m \:g>0\;  et donc : v0>5gL\;v_0>\sqrt{5 \,g \:L}\;,  condition plus restrictive que la précédente.
◊ remarque : entre ces deux limites, le point MM peut atteindre la hauteur du sommet, mais le fil se détend et une partie de la trajectoire est parabolique.
• On aboutit donc à la condition : 2g𝓁>5gL\;2 \,g \:𝓁>5 \,g \:L\; d’où on déduit : d>35𝓁\;d>\frac{3}{5} 𝓁\;.
◊ remarque : il faut aussi probablement d>12𝓁\;d>\frac{1}{2} 𝓁\; pour éviter que le point MM percute le support comportant la fixation en AA , mais cette condition est automatiquement vérifiée dans le cas précédent et même dès que v0>4gL\;v_0>\sqrt{4 \,g \:L}\;.


Énergie potentielle

1.       • Les forces exercées par les deux particules l’une sur l’autre sont opposées (actions réciproques) et ont forcément la même direction que le segment ABAB , compte tenu de la symétrie de l’ensemble (si on suppose que les particules sont effectivement représentables par des points matériels...).
• Si on note u→r\overset{→}{u}_r le vecteur unitaire orienté comme AB⟶\overset{⟶}{AB} (c'est-à-dire radial par rapport à AA ), on peut écrire pour des forces répulsives : F→A→B=αrnu→r\displaystyle \:\overset{→}{F}_{A→B}=\frac{α}{r^n} \: \overset{→}{u}_r\;  et  F→B→A=−αrnu→r\displaystyle \;\overset{→}{F}_{B→A}=-\frac{α}{r^n} \: \overset{→}{u}_r\;.

2.       • S’il existe une énergie potentielle Ep(B)E_p (B) pour la particule BB soumise à l’action de AA , alors on peut écrire : F→A→B=−∇→Ep\; \overset{→}{F}_{A→B}=-\overset{→}{∇}E_p \; où les dérivations sont prises par rapport aux coordonnées de BB .
• Si EpE_p existe, elle doit vérifier : −dEp=dW=F→A→B⋅dOB⟶\; -dE_p=dW=\overset{→}{F}_{A→B}⋅d\overset{⟶}{OB} \;  avec AA fixe si on étudie l’influence sur BB . Mais alors pour n≠1\; n≠1 \;: −dEp=F→A→B⋅dAB⟶=αrnu→r⋅dAB⟶=αrndr=d(−α(n−1)rn−1)\displaystyle \; -dE_p=\overset{→}{F}_{A→B}⋅d\overset{⟶}{AB}=\frac{α}{r^n} \: \overset{→}{u}_r⋅d\overset{⟶}{AB}=\frac{α}{r^n} \:dr=d\left(-\frac{α}{(n-1) \: r^{n-1}}\right) \;  et donc :
Ep=α(n−1)rn−1+Cste\displaystyle E_p=\frac{α}{(n-1) \: r^{n-1}}+Cste .
• De même pour n=1\; n=1 \;: −dEp=αru→r⋅dAB⟶=αrdr=d[αln(r)]\displaystyle \; -dE_p=\frac{α}{r} \: \overset{→}{u}_r⋅d\overset{⟶}{AB}=\frac{α}{r} \, dr=d\left[α \:\ln(r) \right] \;  et donc :
Ep=−αln(r)+CsteE_p=-α \; \ln(r)+Cste .
• On vérifie réciproquement que l’expression ainsi obtenue est solution du problème : F→B→A=−∇→Ep\; \overset{→}{F}_{B→A}=-\overset{→}{∇}E_p \;  où les dérivations sont prises par rapport aux coordonnées de AA .
◊ remarque : puisque Ep=Ep(r)\; E_p=E_p (r) \; la seule dérivée est ∂Ep∂r\displaystyle \; \frac{∂E_p}{∂r} \; et le gradient est : ∇→Ep=∂Ep∂ru→r\displaystyle \; \overset{→}{∇}E_p=\frac{∂E_p}{∂r} \: \overset{→}{u}_r \;.


Énergie cinétique et équation du mouvement

         • Le théorème de l’énergie cinétique peut s’écrire : ∆Ec=W(P→)\; ∆E_c=W(\overset{→}{P} ) \; dans la mesure où la seule autre force intervenant, la tension du fil, ne travaille pas (elle est en permanence normale à la vitesse). Ceci correspond à : ∆Ec=12mv2−0=mg.(z0−z)\; ∆E_c=\frac{1}{2} m \:v^2-0=m \:g .(z_0-z) \;  et donc l’énergie mécanique Em=12mv2+mgz\; E_m=\frac{1}{2} m \:v^2+m \:g \:z \;  est constante.
• Avec l’origine de zz en OO et v=𝓁.|θ˙|\; v=𝓁 .\left|\,\dot{θ} \,\right| on obtient : Em=12m𝓁2θ˙2−mg𝓁cos(θ)=−mg𝓁cos(θ0)\; E_m=\frac{1}{2} m \:𝓁^2 \: \dot{θ}^2-m \:g \:𝓁 \: \cos(θ)=-m \:g \:𝓁 \: \cos(θ_0 ) \;.
• La dérivation de cette relation donne : m𝓁2θ˙θ̈+mg𝓁sin(θ)θ˙=0\; m \:𝓁^2 \: \dot{θ} \: \ddot{θ}+m \:g \:𝓁 \: \sin(θ) \: \dot{θ}=0 \;.  Or la solution θ˙=0\; \dot{θ} =0 \; correspond au cas particulier sans mouvement θ=θ0\; θ=θ_0 \; constant ; le mouvement est donc décrit par l’équation différentielle : θ̈+g𝓁sin(θ)=0\displaystyle \; \ddot{θ}+\frac{g}{𝓁} \: \sin(θ)=0 \;.
◊ remarque : inversement, la quantité constante EmE_m est appelée “intégrale première” du mouvement car elle correspond à une première intégration de l’équation différentielle du mouvement (équation du second ordre qui peut être intégrée deux fois).


Types de mouvements d’un pendule


         		• Dans ce plan l’équation différentielle du mouvement peut être obtenue par la relation fondamentale de la dynamique : ma→=P→+F→\; m \:\overset{→}{a}=\overset{→}{P}+\overset{→}{F} \;.
• La tension F→\overset{→}{F} du fil est initialement dans le plan vertical contenant OO et la direction de v→0\overset{→}{v}_0 . Par la suite, cette force est toujours dans le plan vertical contenant OO et le fil, donc elle ne peut pas faire changer le plan du mouvement ; il en est de même du poids (vertical). Donc le mouvement se fait en entier dans ce plan.
• L’équation différentielle peut ainsi s'écrire en coordonnées polaires : P→+F→=m𝓁θ˙u→θ−m𝓁θ˙2u→r\; \overset{→}{P}+\overset{→}{F}=m \:𝓁 \:\dot{θ} \: \overset{→}{u}_θ-m \:𝓁 \:\dot{θ}^2 \: \overset{→}{u}_r \;.
• La composante orthoradiale donne : m𝓁θ˙=−mgsin(θ)\; m \:𝓁 \:\dot{θ}=-m \:g \: \sin(θ) \;,  donc : θ̈+g𝓁sin(θ)=0\displaystyle \; \ddot{θ}+\frac{g}{𝓁} \: \sin(θ)=0 \;.
• Pour θθ “petit” (imposé si v0v_0 est petite), on obtient : θ̈+g𝓁θ≈0\displaystyle \; \ddot{θ}+\frac{g}{𝓁} \: θ≈0 \; ;  le mouvement est donc de la forme : θ=Θmcos(ωt+φ)\; θ=Θ_m \: \cos(ω \,t+φ) \; avec ω=g𝓁\displaystyle \; ω=\sqrt{\frac{g}{𝓁}} \;.  Les constantes d’intégration se calculent alors d’après les conditions initiales : θ˙=−ωΘmsin(ωt+φ)\; \dot{θ}=-ω \:Θ_m \: \sin(ω \,t+φ) \;  donc : 0=Θmcos(φ)\; 0=Θ_m \: \cos(φ) \;  et  v0𝓁=−ωΘmsin(φ)\displaystyle \; \frac{v_0}{𝓁}=-ω \:Θ_m \: \sin(φ) \;.
Ceci correspond à φ=±π2\; φ=±\frac{π}{2} \;  et  Θm=±v0𝓁ω=±v0𝓁g\displaystyle \; Θ_m=±\frac{v_0}{𝓁 \:ω}=±\frac{v_0}{\sqrt{𝓁 \:g}} \; ;  ces deux expressions mathématiques décrivent le même cas physique ; on choisit alors arbitrairement la description avec Θm=v0𝓁g>0\displaystyle \; Θ_m=\frac{v_0}{\sqrt{𝓁 \:g}}>0 \; et φ=π2\: φ=\frac{π}{2} \;,  donc : θ=Θmsin(ωt)\; θ=Θ_m \: \sin(ω \:t) \;.
• Il est toutefois évident que, même qualitativement (compte tenu de l’approximation du sinus), ce type de mouvement n’est pas le seul possible : il se produit forcément un mouvement d’un autre type si ΘmΘ_m dépasse ππ ; en outre on n’a pas tenu compte du fait que le fil souple ne reste pas forcément tendu.
• La composante radiale de l’équation différentielle du mouvement s’écrit : m𝓁θ˙2=F−mgcos(θ)\; m \:𝓁 \:\dot{θ}^2=F-m \:g \: \cos(θ) \; avec v=𝓁θ˙\; v=𝓁 \:\dot{θ} \; ;  le fil ne reste tendu que si : F=m.[v2𝓁+gcos(θ)]≥0\displaystyle \; F=m .\left[\frac{v^2}{𝓁}+g \: \cos(θ)\right]≥0 \;  donc : v2≥g𝓁cos(θ)\; v^2≥g \:𝓁 \: \cos(θ) \;.
• Si on considère alors les mouvements de type oscillants, il faut vérifier la relation précédente même quand la vitesse s’annule ; ceci impose : cos(θ)≥0\; \cos(θ)≥0 \; et Θm≤π2\; Θ_m≤\frac{π}{2} \;.
• L’énergie mécanique : Em=12mv02=12mv2+mg𝓁.[1−cos(θ)]\; E_m=\frac{1}{2} m \:v_0^{\:2}=\frac{1}{2} m \:v^2+ m \:g \:𝓁 .[1-\cos(θ)] \;  est constante puisque la tension du fil ne travaille pas ; on en déduit : v2=v02−2g𝓁.[1−cos(θ)]\; v^2=v_0^{\:2}-2 \,g \:𝓁 .[1-\cos(θ)] \;.
Par suite, le mobile est en principe capable, si le fil ne se plie pas, de monter jusqu’à ce que v=0\; v=0 \;,  c’est-à-dire : cos(Θm)=1−v022g𝓁\displaystyle \; \cos(Θ_m )=1-\frac{v_0^{\:2}}{2 \,g \:𝓁} \;.  La condition précédente s’écrit donc : v0≤2g𝓁\; v_0≤\sqrt{2 \,g \:𝓁} \;,  limite des mouvements de type oscillatoire.
• Mais d’autre part, si v0v_0 est assez grande pour que la vitesse ne s’annule pas, on peut avoir des mouvements de type rotation périodique à vitesse variable. Ceci correspond aux cas où l’énergie cinétique permet d’atteindre le point à la verticale au dessus de OO sans que le fil se plie.
La première condition s’écrit : v2=v02−2g𝓁.[1−cos(θ)]>0\; v^2=v_0^{\:2}-2 \,g \:𝓁 .[1-\cos(θ)]>0 \; quel que soit θθ ,  donc : v0>4g𝓁\; v_0>\sqrt{4 \,g \:𝓁} \; avec une limite pour θ=π\; θ=π \; et cos(θ)=−1\; \cos(θ)=-1 \;.
La deuxième condition s’écrit : v2+g𝓁cos(θ)>0\; v^2+g \:𝓁 \: \cos(θ)>0 \;  donc  v02−2g𝓁+3g𝓁cos(θ)>0\; v_0^{\:2}-2 \,g \:𝓁+3 \,g \:𝓁 \: \cos(θ)>0 \; pour tout θθ ,  c’est-à-dire : v0>5g𝓁\; v_0>\sqrt{5 \,g \:𝓁} \;.  Cette condition, plus contraignante, limite des mouvements de type rotation périodique à vitesse variable.
• Entre les limites des types de mouvement précédents : 2g𝓁<v0≤5g𝓁\; \sqrt{2 \,g \:𝓁}<v_0≤\sqrt{5 \,g \:𝓁} \;,  le troisième type de mouvement correspond à un début d’oscillation suivi d’une chute parabolique lorsque le fil se plie, ce qui se produit pour v02−2g𝓁+3g𝓁cos(θlim)=0\; v_0^{\:2}-2 \,g \:𝓁+3 \,g \:𝓁 \: \cos(θ_{lim} )=0 \;,  c’est-à-dire pour cos(θlim)=13(2−v02g𝓁)\displaystyle \; \cos(θ_{lim} )=\frac{1}{3} \,\left(2-\frac{v_0^{\:2}}{g \:𝓁}\right) .


Énergie et limite de trajectoire

1.       • La force exercée par la charge fixe qq sur la charge −q-q , mobile selon l’axe OxOx , peut s’exprimer sous la forme : F→=−αq2x2u→x\displaystyle \; \overset{→}{F}=-α \, \frac{q^2}{x^2} \, \overset{→}{u}_x \;  avec  α=14πε0=9.109m.F−1\displaystyle \; α=\frac{1}{4π \:ε_0}=9.10^9 \: \mathrm{m.F^{-1}} .
• S’il existe une énergie potentielle EpE_p pour la charge −q-q soumise à l’action de qq , alors on peut écrire :  F→=−∇→Ep=−dEpdxu→x\displaystyle \;\overset{→}{F}=-\overset{→}{∇}E_p=-\frac{dE_p}{dx} \: \overset{→}{u}_x \;.
• Si EpE_p existe, elle doit vérifier : −dEp=dW=F→⋅dOM⟶=−αq2x2dx=d(αq2x)\displaystyle \; -dE_p=dW=\overset{→}{F}⋅d\overset{⟶}{OM}=-α \, \frac{q^2}{x^2} \: dx=d\left(\frac{α \:q^2}{x}\right) \;  ;  Ep=−αq2x+Cste\displaystyle \; E_p=-\frac{α \:q^2}{x}+Cste \;.
• Pour échapper à l’attraction de la charge fixe qq , la charge mobile doit pouvoir s’éloigner jusqu’à l’infini avec une énergie cinétique Ec≥0\; E_c≥0 \; ;  puisque EpE_p tend vers la constante limite pour xx infini, la conservation de l’énergie mécanique donne : Em=Ec+Ep=12mv02−αq2L+Cste≥Cste\displaystyle \; E_m=E_c+E_p=\frac{1}{2} m \:v_0^{\:2}-\frac{α \:q^2}{L}+Cste≥Cste \;.
• On obtient ainsi : v0≥2αq2mL\displaystyle \; v_0≥\sqrt{\frac{2 \,α \:q^2}{m \:L}} .

2.       • D’une façon analogue : F→=αq2x2u→x\displaystyle \; \overset{→}{F}=α \, \frac{q^2}{x^2} \, \overset{→}{u}_x \;.  Par suite : −dEp=dW=F→⋅dOM⟶=αq2x2dx=d(−αq2x)\displaystyle \; -dE_p=dW=\overset{→}{F}⋅d\overset{⟶}{OM}=α \, \frac{q^2}{x^2} \: dx=d\left(\frac{-α \:q^2}{x}\right) \;  et donc : Ep=αq2x+Cste\displaystyle \; E_p=\frac{α \:q^2}{x}+Cste \;.
• En s’approchant de la charge fixe qq ,  la charge mobile doit avoir une énergie cinétique Ec≥0\; E_c≥0 \; ;  la conservation de l’énergie mécanique s’écrit alors : Em=Ec+Ep=12mv02+αq2L+Cste≥αq2L+Cste\displaystyle \; E_m=E_c+E_p=\frac{1}{2} m \:v_0^{\:2}+\frac{α \:q^2}{L}+Cste≥\frac{α \:q^2}{L}+Cste \;  et la charge mobile s’arrête quand toute l’énergie mécanique est sous forme d’énergie potentielle.
• On obtient ainsi : x≥xm\; x≥x_m \; tel que : 1xm=1L+mv022αq2\displaystyle \; \frac{1}{x_m} =\frac{1}{L}+\frac{m \:v_0^{\:2}}{2 \,α \:q^2} \; ; xm=LDL+D\displaystyle \; x_m=\frac{L \:D}{L+D} \;  avec  D=2αq2mv02\displaystyle \; D=\frac{2 \,α \:q^2}{m \:v_0^{\:2}} \;.


Énergie potentielle et stabilité d’un équilibre

1.       • La force résultante est : F→=(−K1r+K2r2)u→r\displaystyle \; \overset{→}{F}=\left(-K_1 \: r+\frac{K_2}{r^2} \right) \: \overset{→}{u}_r \:  et l’équilibre est obtenu quand cette force s’annule :
−K1r0+K2r02=0\displaystyle -K_1 \: r_0+\frac{K_2}{r_0^{\:2}}=0   d’où on déduit : r0=K2K13\displaystyle \; r_0=\sqrt[3]{\frac{K_2}{K_1}} \;.

2.       • La force dérive d’une énergie potentielle Ep(r)E_p (r) telle que : F→=−∇→Ep\; \overset{→}{F}=-\overset{→}{∇}E_p \; c’est-à-dire : K1r−K2r2=∂Ep∂r\displaystyle \; K_1 \: r-\frac{K_2}{r^2} =\frac{∂E_p}{∂r} \;.  On en déduit : Ep(r)=12K1r2+K2r+Cste\displaystyle \; E_p (r)=\frac{1}{2} K_1 \: r^2+\frac{K_2}{r}+Cste \;.  La valeur particulière Ep(r0)=32K1K223\; E_p (r_0)=\frac{3}{2} \: \sqrt[3]{K_1 \: K_2^{\:2}\,} \; conduit alors à Cste=0\; Cste=0 \;  et  Ep(r)=12K1r2+K2r\displaystyle \; E_p (r)=\frac{1}{2} K_1 \: r^2+\frac{K_2}{r} \;.
◊ remarque : la force est radiale, donc l'énergie potentielle ne dépend pas de θθ .
• L’équilibre par rapport à rr correspond à ∂Ep∂r=0\displaystyle \; \frac{∂E_p}{∂r}=0 \; (extremum) et on retrouve r=r0\; r=r_0 \; ;  la stabilité de cet équilibre est décrite par ∂2Ep∂r2]r=r0=3K1>0\displaystyle \; \left. \frac{∂^2 E_p}{{∂r}^2} \right]_{r=r_0}=3 \,K_1>0 \; (minimum) et l’équilibre est donc stable.
• L’équilibre par rapport aux rotations peut être étudié par l’effet de θθ .  Pour r=r0\; r=r_0 \; fixé, le déplacement est simplement proportionnel aux variations de θθ ; on peut donc raisonner en dérivant par rapport à θθ . L'équilibre correspond à ∂Ep∂θ=0\displaystyle \; \frac{∂E_p}{∂θ}=0 \: et on peut conclure qu’il y a équilibre de rotation pour tout θθ ; la stabilité de cet équilibre est décrite par ∂2Ep∂θ2=0\displaystyle \; \frac{∂^2 E_p}{{∂θ}^2} =0 \; et il s’agit donc d’un équilibre indifférent.


B. EXERCICES D’APPROFONDISSEMENT

Énergie mécanique et équation du mouvement

1.a.    • L’énergie cinétique peut s’écrire :
Ec=12mv2=12m.(x˙2+y˙2+z˙2)=12m.((dxdq)2+(dydq)2+(dzdq)2)q˙2\displaystyle E_c=\frac{1}{2} m \:v^2=\frac{1}{2} m .\left(\dot{x}^2+\dot{y}^2+\dot{z}^2\right)=\frac{1}{2} m .\left(\left(\frac{dx}{dq}\right)^2+\left(\frac{dy}{dq}\right)^2+\left(\frac{dz}{dq}\right)^2 \right) \: \dot{q}^2 .
• Ceci peut s’écrire : Ec=12𝔪(q)q˙2\; E_c=\frac{1}{2} 𝔪(q) \: \dot{q}^2 \;  avec  𝔪(q)=m.((dxdq)2+(dydq)2+(dzdq)2)\displaystyle \; 𝔪(q)=m .\left(\left(\frac{dx}{dq}\right)^2+\left(\frac{dy}{dq}\right)^2+\left(\frac{dz}{dq}\right)^2 \right) \;.


1.b.    • L’énergie potentielle peut s’écrire : Ep(q)=Ep(x(q),y(q),z(q))\; E_p (q)=E_p \left(x(q),y(q),z(q)\right) \;.
• L’énergie mécanique est donc : Em=12𝔪(q)q˙2+Ep(q)\; E_m=\frac{1}{2} 𝔪(q) \: \dot{q}^2+E_p (q) \;.


1.c.    • En l’absence de frottement, le point MM n’est soumis qu’à des forces conservatives de l’énergie (la réaction normale du rail ne travaille pas).
• La dérivation donne : dEmdq=0=12d𝔪dqq˙2+𝔪(q)q˙dq˙dq+dEpdq\displaystyle \; \frac{dE_m}{dq}=0=\frac{1}{2} \frac{d𝔪}{dq} \: \dot{q}^2+𝔪(q) \: \dot{q} \, \frac{d\dot{q}}{dq}+\frac{dE_p}{dq} \;.  Ceci peut se mettre sous la forme : 12𝔪˙q˙+𝔪q̈=−dEpdq\displaystyle \; \frac{1}{2} \dot{𝔪} \: \dot{q}+𝔪 \:\ddot{q}=-\frac{dE_p}{dq} \;.
• On remarque que cela peut correspondre à une “force généralisée” −dEpdq\displaystyle \; -\frac{dE_p}{dq} \; (associée au gradient par rapport à qq ). Par contre, à part éventuels cas particuliers, ceci ne correspond pas à une “quantité de mouvement” 𝔭=𝔪q˙\; 𝔭=𝔪 \:\dot{q} \; qui serait telle que 𝔭˙=−dEpdq\displaystyle \; \dot{𝔭}=-\frac{dE_p}{dq} \;.


1.d.    • Les positions d’équilibre correspondent à q˙=0\; \dot{q}=0 \;  et  q̈=0\; \ddot{q}=0 \;,  donc à dEpdq=0\displaystyle \; \frac{dE_p}{dq}=0 \; (extremums).
• Un équilibre est stable si et seulement si le point matériel, lâché immobile en une position voisine, subit une accélération dans le sens qui tend à le rapprocher de la position d’équilibre. Ceci correspond à 𝔪q̈=−dEpdq\displaystyle \; 𝔪 \:\ddot{q}=-\frac{dE_p}{dq} \; avec 𝔪(q)>0\; 𝔪(q)>0 \; ;  l’accélération se fait donc dans le sens des énergies potentielles décroissantes et l’équilibre est stable si et seulement si d2Epdq2>0\displaystyle \; \frac{d^2 E_p}{{dq}^2} > 0 \; (minimum de EpE_p ).


2.a.    • L’énergie cinétique peut s’écrire : Ec=12mv2\; E_c=\frac{1}{2} m \:v^2 \; avec v¯=dsdt\displaystyle \; \widebar{v}=\frac{ds}{dt} \; d'après la définition de ss (distance parcourue). Ainsi Ec=12ms˙2\; E_c=\frac{1}{2} m \:\dot{s}^2 \; avec donc 𝔪(s)=m\; 𝔪(s)=m \;.
◊ remarque : plus généralement, l'expression se simplifie quand le paramètre qq est une abscisse curviligne proportionnelle à la distance parcourue, ce qui impose 𝔪q̈=−dEpdq\displaystyle \; 𝔪 \:\ddot{q}=-\frac{dE_p}{dq} \;  avec  𝔪(s)=Cste\; 𝔪(s)=Cste \;.


2.b.    • L’énergie mécanique peut s’écrire : Em=12ms˙2+mgz(s)\; E_m=\frac{1}{2} m \:\dot{s}^2+m \:g \:z(s) \;.  La dérivation donne : s̈=−gdzds\displaystyle \; \ddot{s}=-g \, \frac{dz}{ds} \;.


2.c.    • L'oscillateur envisagé ici correspond à : s̈=−kms=−gdzds\displaystyle \; \ddot{s}=-\frac{k}{m} \, s=-g \, \frac{dz}{ds} \;,  donc : dzds=kmgs\displaystyle \; \frac{dz}{ds}=\frac{k}{m \:g} \, s \;  ;  z(s)=k2mgs2\displaystyle \; z(s)=\frac{k}{2 \,m \:g} \, s^2 \;.


2.d.    • D'après ce qui précède : ds2=dx2+dz2=dx2+(ksmg)2ds2\displaystyle \; {ds}^2={dx}^2+{dz}^2={dx}^2+\left(\frac{k \:s}{m \:g}\right)^2 \,{ds}^2 \;.  Ainsi : dx=ds1−(ksmg)2\displaystyle \; dx=ds \:\sqrt{1-\left(\frac{k \:s}{m \:g}\right)^2} \;.
☞ rappel : l'opérateur de différenciation (noté dd ) est prioritaire sur les opérations algébriques ; ainsi : ds2=(ds)2≠d(s2)\; {ds}^2=(ds)^2≠d(s^2) \;.


2.e.    • En posant ksmg=sin(θ2)\displaystyle \; \frac{k \:s}{m \:g}=\sin\left(\frac{θ}{2}\right) \;,  on obtient : dx=dscos(θ2)=mg2kcos2(θ2)dθ=mg4k(1+cos(θ))dθ\displaystyle \; dx=ds \; \cos\left(\frac{θ}{2}\right)=\frac{m \:g}{2 \,k} \: \cos^2\left(\frac{θ}{2}\right) \: dθ=\frac{m \:g}{4 \,k} \,\left(1+\cos(θ) \right) \: dθ \;.
◊ remarque : l'accélération est indirectement provoquée par la pesanteur : |s̈|<g\; \left| \,\ddot{s} \, \right|<g \; ;  ainsi |ksmg|<1\displaystyle \; \left|\frac{k \:s}{m \:g}\right|<1 \;.
◊ remarque : il n'y a pas de problème de signe car |θ2|<π2\displaystyle \; \left|\, \frac{θ}{2} \,\right|<\frac{π}{2} \; donc cos(θ2)>0\; \cos\left(\frac{θ}{2}\right)>0 \;.
• Compte tenu du fait que x=0\; x=0 \; correspond à z=0\; z=0 \;,  qui correspond à s=0\; s=0 \;,  donc à θ=0\; θ=0 \;,  ceci donne : x=mg4k(θ+sin(θ))\displaystyle \; x=\frac{m \:g}{4 \,k} \:\left(θ+\sin(θ) \right) \;.


2.f.    • L'expression de x(θ)x(θ) n'est pas facile à inverser pour en déduire z(x)=z(s(θ(x)))\; z(x)=z(s(θ(x))) \;.  On peut toutefois préciser la description paramétrique en fonction de θθ : z=mg2ksin2(θ2)=mg4k(1−cos(θ))\displaystyle \; z=\frac{m \:g}{2 \,k} \: \sin^2\left(\frac{θ}{2}\right)=\frac{m \:g}{4 \,k} \:\left(1-\cos(θ) \right) \;.
• La représentation paramétrique {x=mg4k(θ+sin(θ));z=mg4k(1−cos(θ))}\displaystyle \; \left\{x=\frac{m \:g}{4 \,k} \:\left(θ+\sin(θ) \right) \: \,;\, z=\frac{m \:g}{4 \,k} \:\left(1-\cos(θ) \right)\right\} \; décrit une cycloïde.
◊ remarque : on peut inversement exprimer x(z)x(z) mais l'expression compliquée n'apporte rien de plus.


Énergie mécanique et équation du mouvement

1.a.    • L’énergie cinétique peut s’écrire :
Ec=12mv2=12m.(x˙2+z˙2)=12m.(1+(dzdx)2)x˙2\displaystyle E_c=\frac{1}{2} m \:v^2=\frac{1}{2} m .(\dot{x}^2+\dot{z}^2)=\frac{1}{2} m .\left(1+\left(\frac{dz}{dx}\right)^2 \right) \;\dot{x}^2 .
• Ceci peut s’écrire : Ec=12𝔪(x)x˙2\; E_c=\frac{1}{2} 𝔪(x) \: \dot{x}^2 \;  avec  𝔪(x)=m.(1+(dzdx)2)\displaystyle \; 𝔪(x)=m .\left(1+\left(\frac{dz}{dx}\right)^2 \right) \;.


1.b.    • L’énergie potentielle peut s’écrire : Ep(x)=mgz(x)\; E_p (x)=m \:g \:z(x) \;.
• L’énergie mécanique est donc : Em=12𝔪(x)x˙2+mgz(x)\; E_m=\frac{1}{2} 𝔪(x) \: \dot{x}^2+m \:g \:z(x) \;.


1.c.    • En l’absence de frottement, le point MM n’est soumis qu’à des forces conservatives de l’énergie (la réaction normale du rail ne travaille pas).
• La dérivation donne :
dEmdx=12d𝔪dxx˙2+𝔪(x)x˙dx˙dx+mgdzdx=dzdxd2zdx2x˙2+(1+(dzdx)2)ẍ+gdzdx=0\displaystyle \frac{dE_m}{dx}=\frac{1}{2} \frac{d𝔪}{dx} \, \dot{x}^2+𝔪(x) \: \dot{x} \: \frac{d\dot{x}}{dx}+m \:g \, \frac{dz}{dx}=\frac{dz}{dx} \, \frac{d^2 z}{{dx}^2} \, \dot{x} ^2+\left(1+\left(\frac{dz}{dx}\right)^2 \right) \: \ddot{x}+g \: \frac{dz}{dx}=0 .


2.a.    • L’équation différentielle pour l’oscillateur harmonique donne : ẍ=−kmx\displaystyle \; \ddot{x}=-\frac{k}{m} \, x \;.
• En substituant (1+(dzdx)2)x˙2=2(Emm−gz)\displaystyle \; \left(1+\left(\frac{dz}{dx}\right)^2 \right) \; \dot{x}^2=2 \:\left(\frac{E_m}{m}-g \:z\right) \;,  on en déduit une équation différentielle du second ordre sur z(x)z(x) : −(1+(dzdx)2)2kmx+dzdx[g.(1+(dzdx)2)+2(Emm−gz)d2zdx2]=0\displaystyle \; -\left(1+\left(\frac{dz}{dx}\right)^2 \right)^2 \, \frac{k}{m} \: x+\frac{dz}{dx} \, \left[g .\left(1+\left(\frac{dz}{dx}\right)^2 \right)+2 \:\left(\frac{E_m}{m}-g \:z\right) \: \frac{d^2 z}{{dx}^2} \right]=0 \;.


2.b.    • L’oscillation se fait autour d’une position d’équilibre stable, correspondant à un minimum de EpE_p donc de z(x)z(x) . On peut donc choisir ce point comme origine, ce qui impose : z(0)=0\; z(0)=0 \;  et  dzdx(0)=0\displaystyle \; \frac{dz}{dx}(0)=0 \;.  On en déduit la valeur C=0\; C=0 \;.


2.c.    • Le logiciel Maple trouve une intégrale première : −(1+(dzdx)2)kmx2+2(Emm+gz)d2zdx2=0\displaystyle \; -\left(1+\left(\frac{dz}{dx}\right)^2 \right) \, \frac{k}{m} \, x^2+2 \,\left(\frac{E_m}{m}+g \:z\right) \: \frac{d^2 z}{{dx}^2} =0 \; mais ne trouve pas de solution formelle de cette dernière.
• Faute de mieux on peut tenter une résolution sous forme de développement en série (c'est un peu plus simple en partant de l'intégrale première) : la symétrie impose : z(x)≈αx2+βx4+𝒪(x6)\; z(x)≈α \:x^2+β \:x^4+𝒪(x^6) \;.
• On en déduit : α=mg8Em(1+8Emkm2g2−1)\displaystyle \; α=\frac{m \:g}{8 \,E_m} \, \left(\sqrt{1+\frac{8 \,E_m \: k}{m^2 \: g^2}}-1\right) \;  puis  β=2α2k16Emα+mg\displaystyle \; β=\frac{2 \,α^2 \: k}{16 \,E_m \: α+m \:g} \; (et ainsi de suite éventuellement).
• Une autre méthode consiste à isoler : dzdx=kx2−2mgz2Em−kx2\displaystyle \; \frac{dz}{dx}=\sqrt{\frac{k \:x^2-2 \,m \:g \:z}{2 \,E_m-k \:x^2}} \;  puis à utiliser la méthode d’Euler.
• Pour que le calcul soit possible, il faut que l'amplitude maximale zmax=z(xmax)=Emmg\displaystyle \; z_{max}=z(x_{max})=\frac{E_m}{m \:g} \;  soit atteinte avant que la tangente au rail devienne verticale : xext=2Emk\displaystyle \; x_{ext}=\sqrt{\frac{2 \:E_m}{k}} \;,  forcément à l'extrémité du rail.
Ceci implique de limiter EmE_m pour un rail donné (dont la forme est imposée par kk ), mais pour une raideur donnée, la forme du rail dépend aussi de EmE_m (donc de l'amplitude du mouvement souhaité) !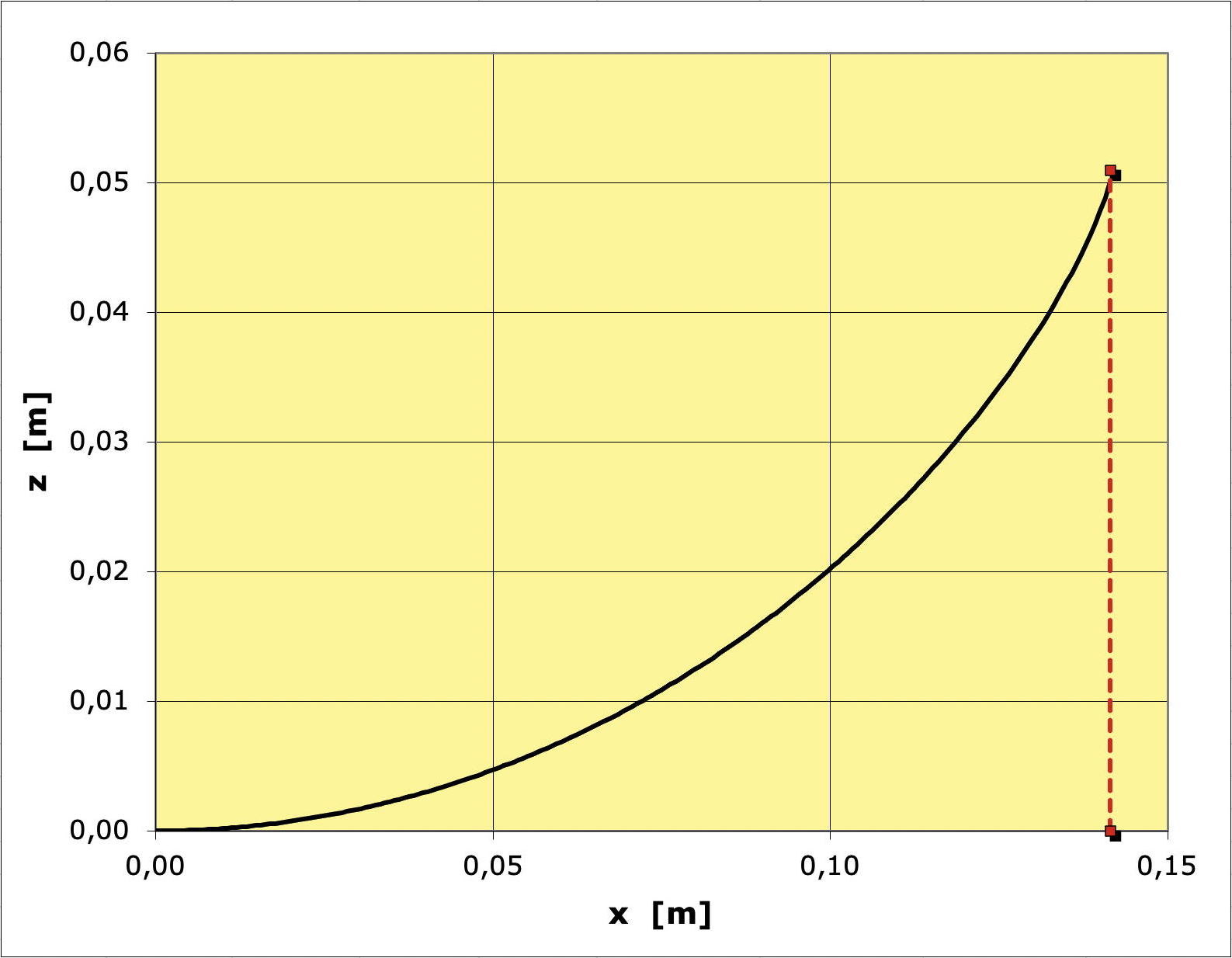

dynEnergie_cor_Im/dynEnergie_cor_Im2.jpg


2.d.    • L’oscillateur harmonique correspond à : x(t)=Asin(ωt+φ)\; x(t)=A \; \sin(ω \,t+φ) \; avec ω=km\displaystyle \; ω=\sqrt{\frac{k}{m}} \;  et  A=2Emk\displaystyle \; A=\sqrt{\frac{2 \,E_m}{k}} \;.  Ceci donne x˙(t)=Aωcos(ωt+φ)\; \dot{x}(t)=A \:ω \; \cos(ω \,t+φ) \;  puis  x˙2=km(A2−x2)\displaystyle \; \dot{x}^2=\frac{k}{m} \left(A^2-x^2 \right) \;.
• Cela donne : dzdxd2zdx2km(A2−x2)−(1+(dzdx)2)kmx=−gdzdx\displaystyle \: \frac{dz}{dx} \, \frac{d^2 z}{{dx}^2} \, \frac{k}{m} \left(A^2-x^2 \right)-\left(1+\left(\frac{dz}{dx}\right)^2 \right) \frac{k}{m} \: x=-g \: \frac{dz}{dx} \;.


2.e.    • L’équation précédente peut se simplifier en posant Z(x)=dzdx\displaystyle \; Z(x)=\frac{dz}{dx} \;:
ZdZdxkm(A2−x2)−(1+Z2)kmx=−gZ\displaystyle Z \: \frac{dZ}{dx} \, \frac{k}{m} \left(A^2-x^2 \right)-\left(1+Z^2 \right) \frac{k}{m} \, x=-g \:Z .
• Le logiciel Maple ne trouve pas de solution formelle ; faute de mieux on peut tenter une résolution sous forme de développement en série : la symétrie impose : Z(x)≈2αx+4βx3+𝒪(x5)\; Z(x)≈2 \,α \:x+4 \,β \:x^3+𝒪(x^5) \;.
• On en déduit : α=mg4kA2(1+4A2k2m2g2−1)\displaystyle \; α=\frac{m \:g}{4\,k \:A^2} \left(\sqrt{1+\frac{4 \,A^2 \: k^2}{m^2 \: g^2}}\:-1\right) \;  puis  β=2α2k8kA2α+mg\displaystyle \: β=\frac{2 \,α^2 \: k}{8 \,k\:A^2 \: α+m \:g} \: (et ainsi de suite éventuellement).
• Une autre méthode consiste à isoler : dZdx=(1+Z2)kx−mgZZ.(2Em−kx2)\displaystyle \; \frac{dZ}{dx}=\frac{\left(1+Z^2 \right)\: k \:x-m \:g \:Z}{Z .(2 \,E_m-k \:x^2 )} \;  puis à utiliser la méthode d’Euler.
◊ remarque : cela impose de simplifier astucieusement le début du calcul, pour lequel Z(0)=0\; Z(0)=0 \; ;  on peut utiliser : dZdx(0)=k.[xZ]0−mg2Em\displaystyle \; \frac{dZ}{dx}(0)=\frac{k.\left[\frac{x}{Z}\right]_0-m \:g}{2 \,E_m} \;  avec  [xZ]0=12α\displaystyle \; \left[\frac{x}{Z}\right]_0=\frac{1}{2 \,α} \; (ce qui nécessite d'étudier le développement limité).