ÉTUDE EXPÉRIMENTALE DES FORCES - corrigé du TP


Modélisation des forces de frottement

Préparation de l’enregistrement

• Le palet utilisé a une masse de 630±1g\; 630±1 \:\mathrm{g} \;.  La mesure de la masse de l’anneau magnétique est moins facile à cause des effets magnétiques sur la balance ; on obtient 665±10g\; 665±10 \:\mathrm{g} \; par élongation d’un ressort ; on obtient 680±5g\; 680±5 \:\mathrm{g} \; en utilisant un tube intermédiaire en papier fort pour éviter l'interaction avec la balance.

Modèle du frottement fluide (visqueux)

• Pour les faibles vitesses, le frottement fluide est proportionnel à la vitesse : f→=−kv→\; \overset{→}{f}=-k \:\overset{→}{v} \;  avec k>0 \; k>0 .

Algébriquement (pour le mouvement rectiligne) : f¯=−kv\; \widebar{f}=-k \:v \; ;  compte tenu de la compensation du poids par la réaction normale de la table, la relation fondamentale de la dynamique peut donc s’écrire : mv˙=−kv \; m \:\dot{v}=-k \:v .  L’intégration donne alors : v=v0e−kt/m \; v=v_0 \: \mathrm{e}^{-kt/m}   et  ln({v})=ln({v0})−kmt\displaystyle \; \ln(\{v\})=\ln(\{v_0\})-\frac{k}{m} \: t .

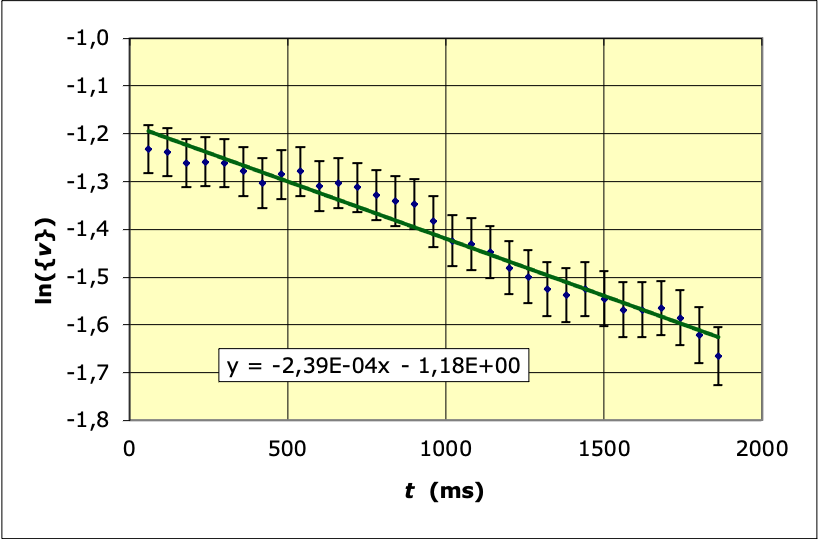
dynEnergie_corTP_Im/dynEnergie_corTP_Im1.png

• On constate que les données sont effectivement compatibles avec ce modèle (la droite ne sort pas des intervalles d’incertitude).

L’ajustement donne :  ln({v0})=ln(v01m.s−1)=−1,181±0,018\displaystyle \ln\left(\{v_0\}\right) =\ln\left(\frac{v_0}{1 \:\mathrm{m.s^{-1}}}\right) =-1\text{,}181±0\text{,}018  (c’est-à-dire v0=0,307±0,006m.s−1 \; v_0=0\text{,}307±0\text{,}006 \:\mathrm{m.s^{-1}} )  et la constante : km=0,239±0,018s−1\displaystyle \; \frac{k}{m}=0\text{,}239±0\text{,}018 \:\mathrm{s^{-1}} \; (c’est-à-dire k=0,313±0,024kg.s−1 \; k=0\text{,}313±0\text{,}024 \:\mathrm{kg.s^{-1}} ).

• En ce qui concerne la précision, les incertitudes sur le modèle (de l'ordre de 5%5 \:% ) découlent logiquement de celles sur les données.

Celles-ci peuvent généralement provenir de plusieurs causes :

• Dans la mesure où le frottement est faible, et présente des fluctuations qui limitent un peu la précision du modèle, on peut envisager de simplifier celui-ci en utilisant un développement limité (bien que la vitesse varie presque du simple au double pour le mouvement étudié) : v≈v0.(1−kmt) \displaystyle \; v≈v_0 .\left(1-\frac{k}{m} \, t\right) .

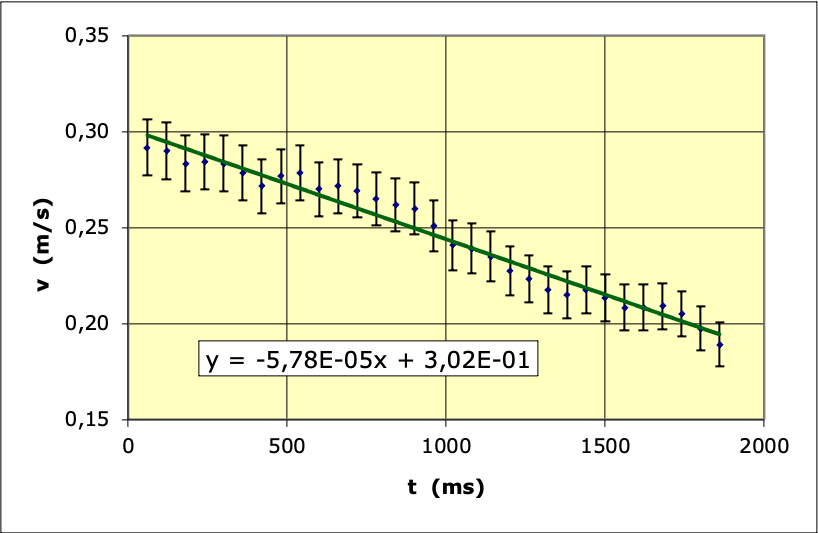
dynEnergie_corTP_Im/dynEnergie_corTP_Im2.png

La représentation est aussi correcte que la précédente (la droite ne sort pas des intervalles d’incertitude).

L’ajustement donne : v0=0,302±0,005m.s−1\; v_0=0\text{,}302±0\text{,}005 \:\mathrm{m.s^{-1}} \; (tout à fait compatible avec la détermination précédente) et la constante : km=0,191±0,018s−1\displaystyle \; \frac{k}{m}=0\text{,}191±0\text{,}018 \:\mathrm{s^{-1}} \; correspondant à : k=0,251±0,023kg.s−1\; k=0\text{,}251±0\text{,}023 \:\mathrm{kg.s^{-1}} \; (valeur un peu différente, mais non incompatible avec la détermination précédente).

• La précision est semblable à celle de la version non simplifiée du modèle (la précision des mesures est insuffisante pour faire la différence entre les deux) ; ceci justifie l'approximation.

Modèle du frottement solide

• Pour les situations où il y a glissement, le frottement solide est à peu près constant : f→=−fu→\; \overset{→}{f}=-f \;\overset{→}{u} \;  où u→=v→v\displaystyle \; \overset{→}{u}=\frac{\overset{→}{v}}{v} \; est un vecteur unitaire orienté selon le mouvement.

• Algébriquement (pour le mouvement rectiligne), la relation fondamentale de la dynamique peut s’écrire : mv˙=−f \; m \:\dot{v} = -f .  L’intégration donne alors : v=v0−fmt\displaystyle \; v=v_0-\frac{f}{m} \, t \; (tant qu’il y a glissement, c’est-à-dire tant que v>0 \; v>0 ).

La représentation graphique de v(t)v(t) en fonction de tt est donc la même que précédemment (tout à fait compatible avec le modèle) ; on peut en déduire la valeur de la constante : f=kv0=76±5mN \; f=k \:v_0=76±5 \:\mathrm{mN} .

• La précision est raisonnable, mais surtout : l'approximation du premier ordre pour un frottement fluide correspond au même type d’expression qu’un frottement solide.

Ceci permet de simplifier la prise en compte des frottements : tant qu’ils sont faibles, il suffit de les décrire “globalement” par un frottement de type “solide”, plus facile à utiliser pour les calculs (même si en réalité les deux types de frottements interviennent à la fois).

Modélisation des forces magnétiques

Préparation de l’enregistrement

• On mesure le diamètre dd (extérieur) d’un anneau magnétique, afin de pouvoir vérifier que les palets n'ont pas eu de choc “dur” dans leur positions les plus proches de l’interaction : d=129mm \; d=129 \:\mathrm{mm} .

On mesure aussi le diamètre d’d\text{’} (moyen) d’un anneau magnétique, afin de pouvoir étudier en fonction de la distance entre les milieux des aimants les plus proches au moment de l’interaction : d’=116mm \; d\text{’}=116 \:\mathrm{mm} .

Modélisation avec une énergie potentielle magnétique

• On suppose que les forces magnétiques entre les deux anneaux dérivent d’une énergie potentielle de la forme : Ep=αrn\displaystyle \; E_p=\frac{α}{r^n} \;  avec r=OM\; r=OM \; ; α>0\; α>0 \; ; n∈N \; n∈N .

• Si on raisonne algébriquement, avec l’abscisse curviligne LL , la conservation de l’énergie mécanique peut s’écrire : 12mv2+αrn=12mv02+αr0n \displaystyle \; \frac{1}{2} m \:v^2+\frac{α}{r^n} =\frac{1}{2} m \:v_0^{\:2}+\frac{α}{r_0^{\:n}} ,  c’est-à-dire : v2+Arn=v02+Ar0n\displaystyle \; v^2+\frac{A}{r^n} =v_0^{\:2}+\frac{A}{r_0^{\:n}} \;  avec  A=2αm \displaystyle \; A=\frac{2 \,α}{m} .

Si on suppose l’exposant nn assez grand, alors la condition expérimentale r0≫rmin\; r_0≫r_{min} \; permet de négliger Ar0n\displaystyle \; \frac{A}{r_0^{\:n}} \; en très bonne approximation. On en déduit alors : v02−v2≈Arn\displaystyle \; v_0^{\:2}-v^2≈\frac{A}{r^n} \;  et   ln({v02−v2})≈ln({A})−nln({r})\ln\left(\{v_0^{\:2}-v^2 \}\right)≈\ln(\{A\})-n \; \ln(\{r\}) .

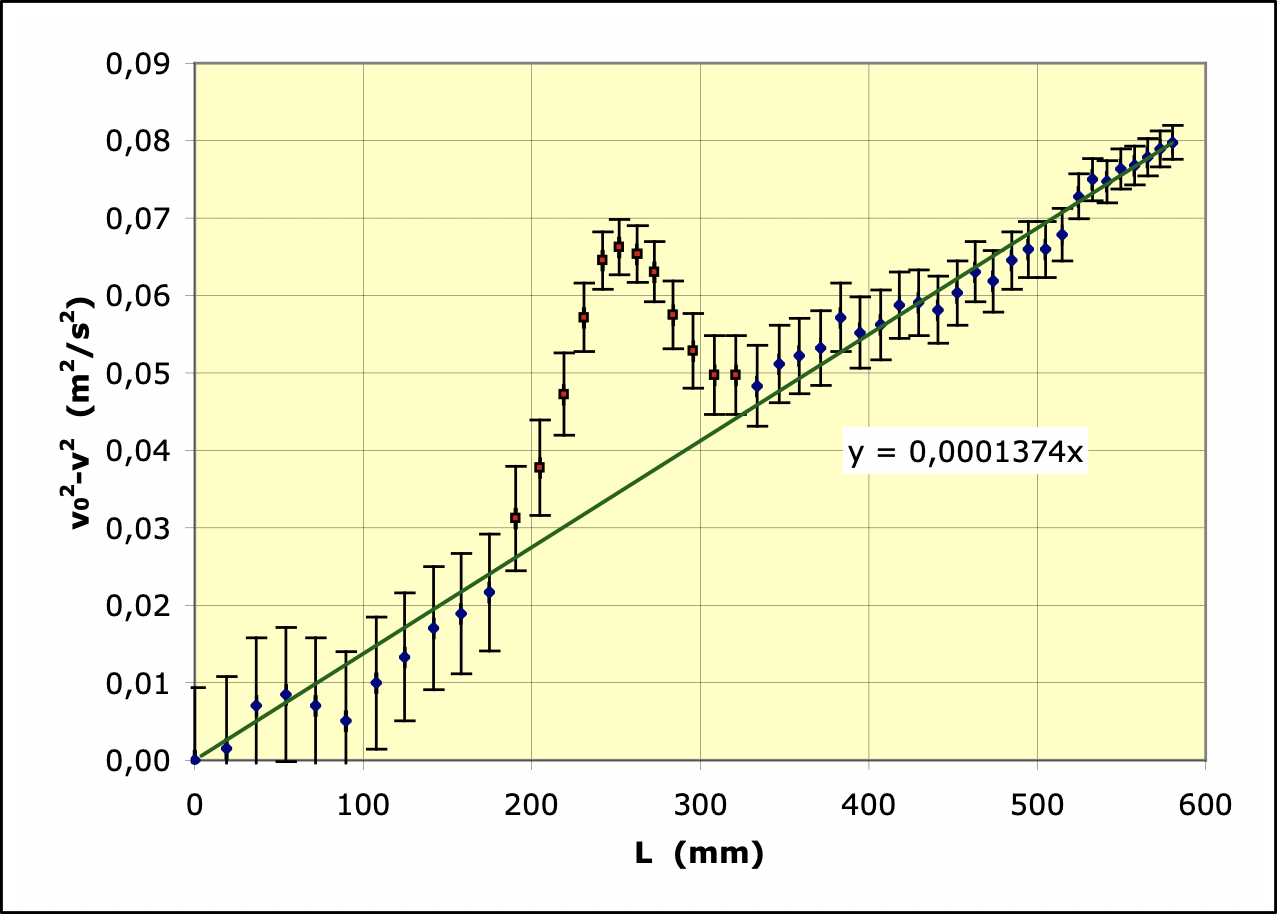
• La représentation de  ln({v02−v2})\ln\left(\{v_0^{\:2}-v^2\} \right)  en fonction de  ln({r})\ln(\{r\})  est la suivante :

dynEnergie_corTP_Im/dynEnergie_corTP_Im3.png

L’ajustement des paramètres est alors totalement inutile puisqu’il est évident que le modèle est insuffisant : l’énergie potentielle magnétique ne serait pas la même à l’aller et au retour (même en se limitant à la zone proche du choc) ; il faut donc reprendre les calculs en tenant compte des frottements.

Prise en compte des frottements

• Conformément à la conclusion de la partie (1.), on suppose que les frottements peuvent être décrits par le modèle de frottement solide : f→=−fu→ \; \overset{→}{f}=-f \;\overset{→}{u} .

En raisonnant algébriquement (avec l’abscisse curviligne LL ), la variation de l’énergie mécanique est égale au travail (résistant) des frottements. On obtient ainsi : 12mv2+αrn=12mv02+αr0n−fL\displaystyle \; \frac{1}{2} m \:v^2+\frac{α}{r^n} =\frac{1}{2} m \:v_0^{\:2}+\frac{α}{r_0^{\:n}}-f \:L \;  ce qui peut s’écrire sous la forme : v2+Arn=v02+Ar0n−CL\displaystyle \; v^2+\frac{A}{r^n} =v_0^{\:2}+\frac{A}{r_0^{\:n}}-C \:L \;  avec A=2αm\displaystyle \; A=\frac{2 \,α}{m} \; et C=2fm \displaystyle \; C=\frac{2 \,f}{m} .

Si on suppose l’exposant nn assez grand, alors en limitant l'étude aux points tels que r≫rmin\; r≫r_{min} \; on peut négliger Arn\displaystyle \; \frac{A}{r^n} \; en bonne approximation. 0n obtient alors la relation “asymptotique” : v02−v2≈CL \; v_0^{\:2}-v^2≈C \:L .

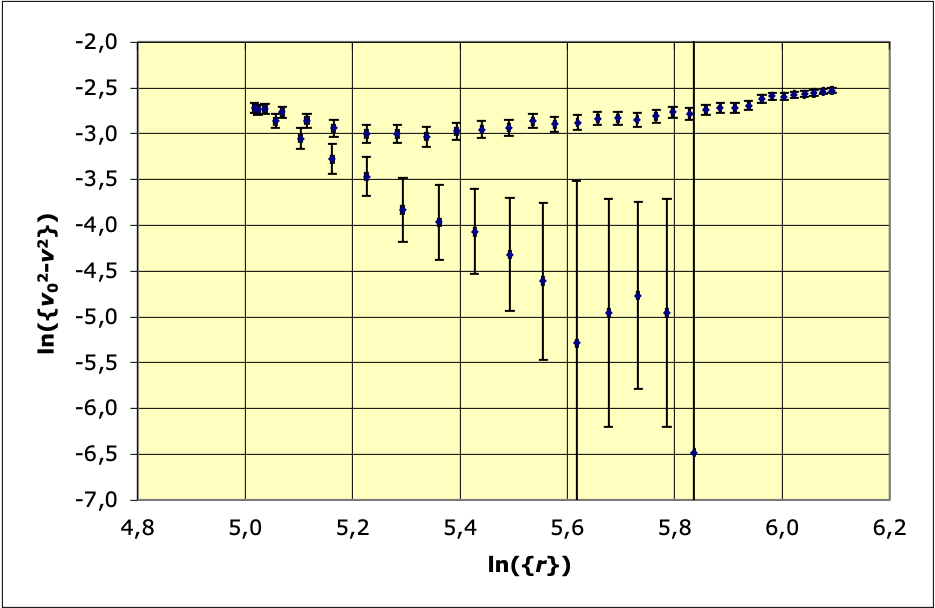
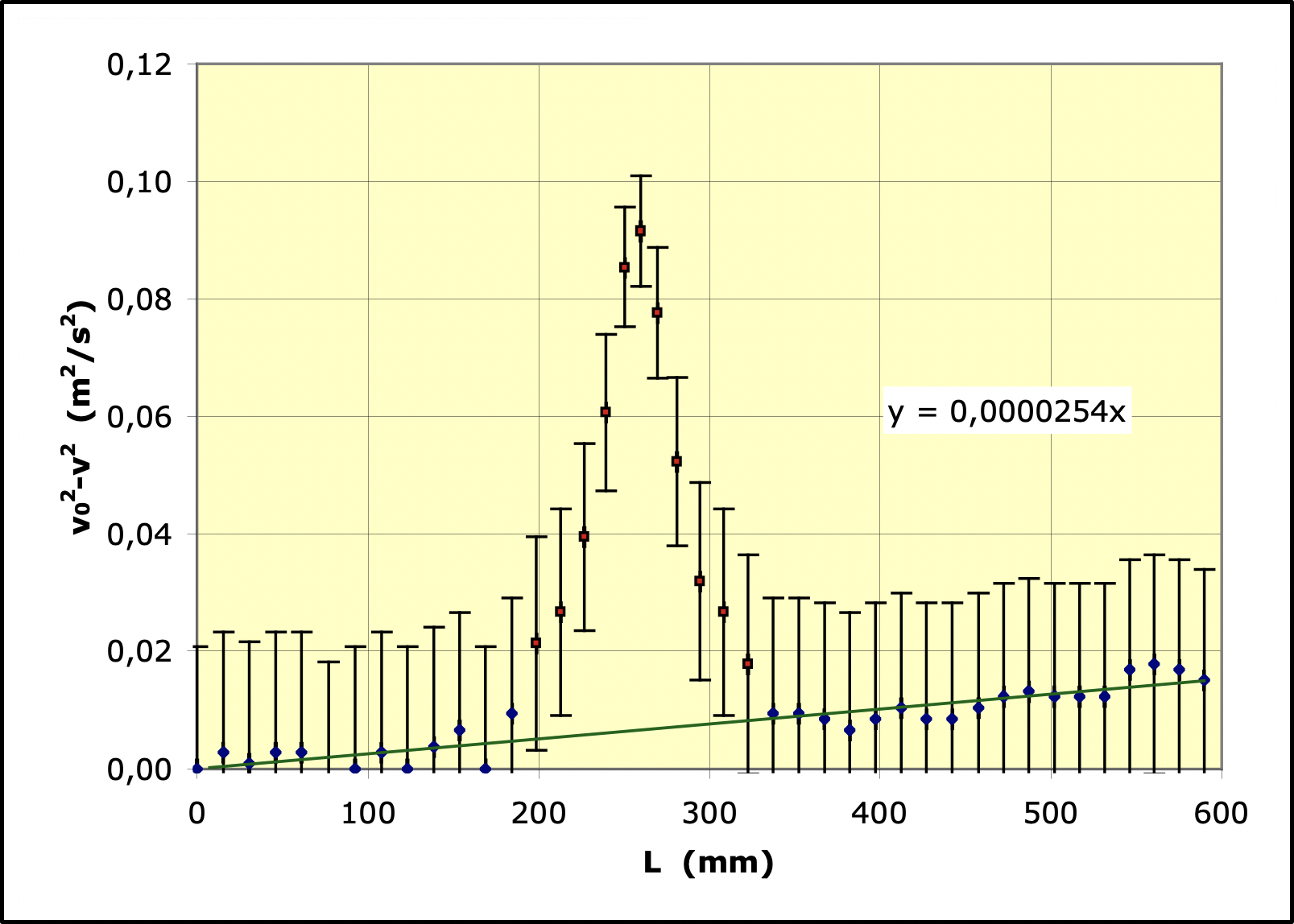
• La représentation de v02−v2\; v_0^{\:2}-v^2 \; en fonction de LL est la suivante :

dynEnergie_corTP_Im/dynEnergie_corTP_Im4.png

On y constate effectivement, mise à part la “bosse” correspondant à l’énergie magnétique (lorsque les deux palets sont proches), une croissance linéaire correspondant à la perte d’énergie par frottement.

◊ remarque : la valeur de l’abscisse curviligne LL est ici “décalée d’un point” par rapport à celle utilisée pour calculer les vitesses (le calcul de la vitesse au point n° 1 nécessite de connaître la position du point n° 0 ).

• L’ajustement donne : C=0,1374±0,0015m.s−2\; C=0\text{,}1374±0\text{,}0015 \:\mathrm{m.s^{-2}} \; c’est-à-dire : f=90±1mN\; f=90±1 \:\mathrm{mN} \; (comparable à la détermination précédente, compte tenu des variations de frottement constatées).

• Pour les points proches de OO ,  on peut négliger Ar0n\displaystyle \; \frac{A}{r_0^{\:n}} \; en très bonne approximation, mais il faut tenir compte de Arn\displaystyle \; \frac{A}{r^n} \;.  Ces points sont ceux qui n’ont pas été pris en compte dans la représentation linéaire précédente ; ce sont les seuls au contraire qui sont considérés maintenant (les autres donneraient v02−v2−CL≈0 \; v_0^{\:2}-v^2-C \:L≈0 ).

◊ remarque : du point de vue de la précision de ce modèle, le graphique précédent montre clairement que la “bosse” correspondant à l’énergie potentielle magnétique est effectivement négligeable dès que les deux palets s’éloignent, c’est-à-dire que le terme Ar0n\displaystyle \; \frac{A}{r_0^{\:n}} \; est tout à fait négligeable.

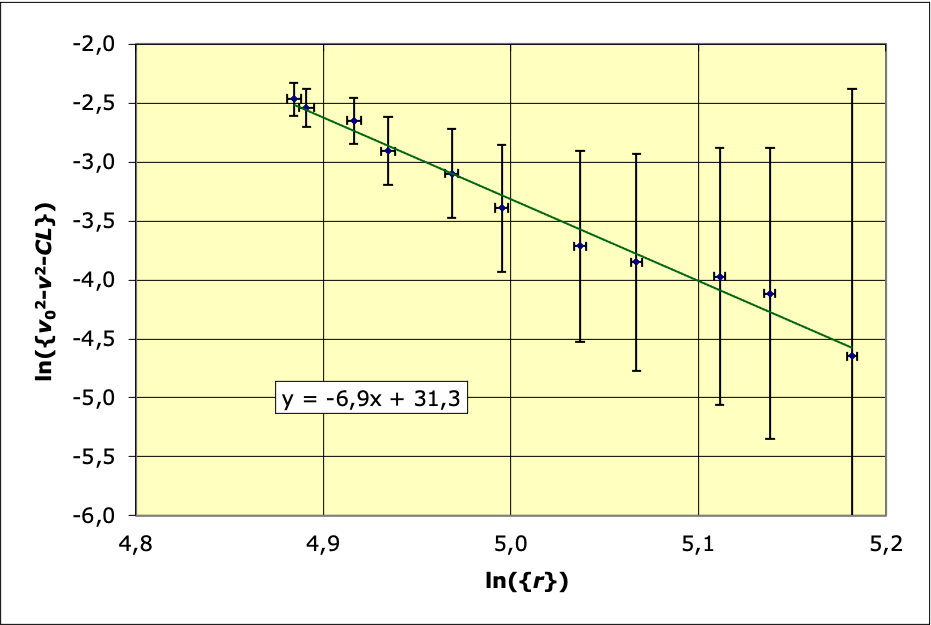
• La représentation de  ln({v02−v2−CL})\ln\left(\{v_0^{\:2}-v^2-C \:L\}\right)  en fonction de ln({r})\ln(\{r\}) est la suivante :

dynEnergie_corTP_Im/dynEnergie_corTP_Im5.png

L’ajustement donne : n=7,5±1,9\; n=7\text{,}5±1\text{,}9 \;  et   ln({A})=34,1±9,7\ln(\{A\})=34\text{,}1±9\text{,}7  (c’est-à-dire α≈4.1014±4J.mn \; α≈4.{10}^{14±4} \: \mathrm{J.m^n} ).

◊ remarque : ce graphique montre une représentation satisfaisante, mais l’énergie potentielle magnétique (petite) est calculée par différence des autres énergies (beaucoup plus grandes) et la précision nécessite que lors de l'interaction les deux palets s'approchent presque jusqu'au contact.

Amélioration par cumul de plusieurs séries de mesures

• Puisque les données finales ne dépendent que de l’énergie magnétique, (identique avec les mêmes palets), on peut cumuler ces données pour essayer d’améliorer le résultat final par effet statistique.

• On obtient ainsi pour un autre choc : C=0,025±0,010m.s−2\; C=0\text{,}025±0\text{,}010 \:\mathrm{m.s^{-2}} \; c’est-à-dire : f=17±7mN\; f=17±7 \:\mathrm{mN} \; (valeur inférieure aux précédentes, mais les palets n’ont pas des coussins d’air tous aussi performants) :

dynEnergie_corTP_Im/dynEnergie_corTP_Im6.png

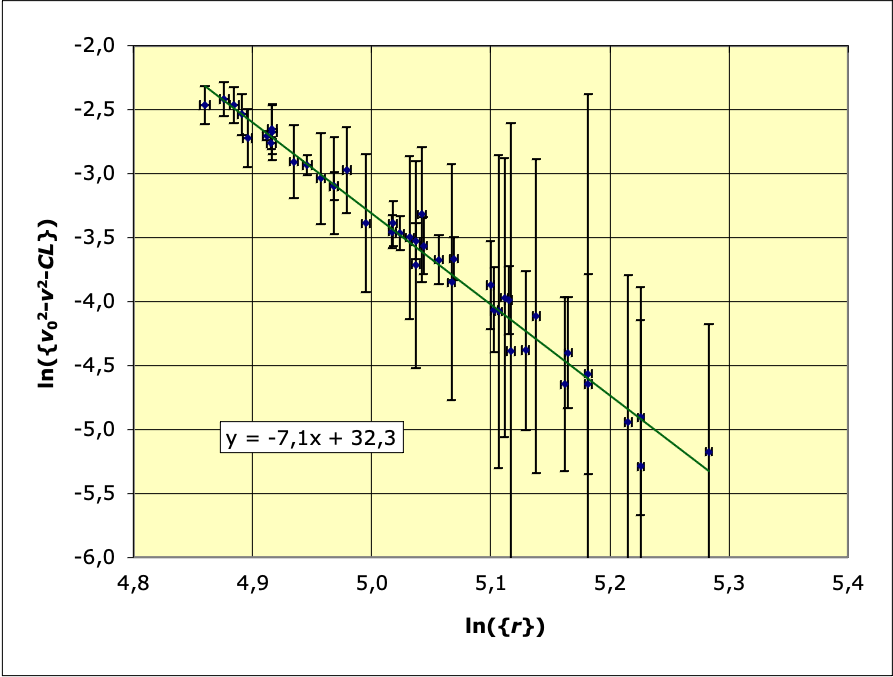
• La représentation de  ln({v02−v2−CL})\ln\left(\{v_0^{\:2}-v^2-C \:L\}\right)  en fonction de  ln({r})\ln(\{r\})  est la suivante :

dynEnergie_corTP_Im/dynEnergie_corTP_Im7.png

L’ajustement donne : n=6,9±1,6\; n=6\text{,}9±1\text{,}6 \;  et   ln({A})=31±8\ln(\{A\})=31±8  (c’est-à-dire α≈3.101±3J.mn \; α≈3.{10}^{1±3} \: \mathrm{J.m^n} ).

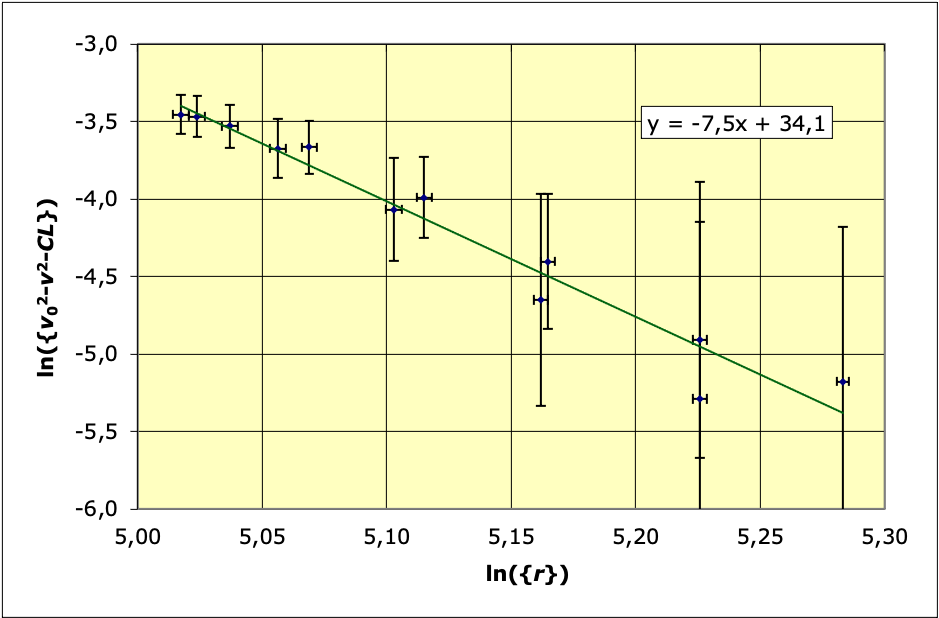
• Puisque les différentes séries de données semblent compatibles, on peut envisager de les cumuler ; avec quatre séries on obtient le graphique suivant :

dynEnergie_corTP_Im/dynEnergie_corTP_Im8.png

L’ajustement donne : n=7,1±0,8\; n=7\text{,}1±0\text{,}8 \;  et   ln({A})=32±4\ln(\{A\})=32±4  (c’est-à-dire α≈7.1013±2J.mn \; α≈7.{10}^{13±2} \: \mathrm{J.m^n} ).

Ceci permet donc de diminuer les incertitudes, mais celle pour αα est encore totalement inacceptable et il n’est pas simple d’envisager le cumul de plusieurs dizaines de séries de mesure pour améliorer de façon radicale.

• Il est alors intéressant d'envisager une légère modification des notations du modèle : le calcul de αα est imprécis parce que (puisque rr est utilisé avec des mesures en mm\mathrm{mm} ) il correspond à l'extrapolation du modèle jusqu'à des distances sans rapport avec les conditions expérimentales ( r≈2Rr≈2 \,R  à  3R3 \,R ).

En utilisant au contraire une expression de la forme Ep=βdnrn\displaystyle \; E_p=β \: \frac{d^n}{r^n} \;  avec d=2R=129±1mm\; d=2 \,R=129±1 \:\mathrm{mm} \; on obtient plus raisonnablement α≈(7,0±0,2).1013J.mn \; α≈(7\text{,}0±0\text{,}2).{10}^{13} \: \mathrm{J.m^n} .

◊ remarque : si l'ordonnée à l'origine est très éloignée des points mesurés, elle est à la fois peu contrainte et très corrélée à la pente, d'où des incertitudes anormalement exagérées.

• En ce qui concerne l'exposant, on peut montrer que deux aimants droits alignés et de sens contraires se repoussent avec une force qui, en première approximation (pour des distances qui ne sont pas trop petites), dérive d’une énergie potentielle en 1r3 \displaystyle \; \frac{1}{r^3} .  On peut alors essayer d’intégrer l’effet des multiples aimants entourant un anneau sur les multiples aimants entourant l’autre anneau.

L’intégrale (double) est assez complexe, mais on peut calculer numériquement Ep(r)E_p (r) et comparer à αrn\displaystyle \; \frac{α}{r^n} \; au moyen d'un graphique logarithmique semblable au précédent :

Cette comparaison ne met en évidence aucune incompatibilité, mais elle est encore loin de confirmer la validité du modèle proposé. L'exposant nn expérimental semble un peu faible, mais la théorie envisagée suppose des moments dipolaires quasi ponctuels et permanents, approximation probablement médiocre lorsque les anneaux sont proches (la taille des aimants n'est pas négligeable et ils subissent en outre des effets induits tendant à diminuer leur aimantation).

◊ remarque : évidemment, on peut proposer d'autres approches que la méthode énergétique ; par exemple en mesurant la force (en fonction de la distance) par une méthode statique (dynamomètres à ressort), ou par une méthode dynamique (calcul du vecteur accélération) ; il serait intéressant que certains groupes de TP fassent preuve d'un peu d'audace...