M. I - DYNAMIQUE ; PRINCIPE FONDAMENTAL

Masse et principe d’inertie

Masse

• Il est plus facile de mettre en mouvement horizontal (indépendant du poids) une balle qu’une locomotive ; de même pour arrêter le mouvement.

On appelle “masse” la grandeur physique exprimant la “tendance” à résister aux variations du mouvement ; on nomme “inertie” sa propriété.

• La masse, qui différencie la “dynamique” de la “cinématique”, est supposée (en mécanique non relativiste) :

indépendante du mouvement et du référentiel ;
indépendante du temps et du lieu ;
additive : la masse totale est la somme des masses des constituants.

• On constate par ailleurs qu’au voisinage de la Terre (entre autres) les corps sont d’autant plus pesants qu’ils sont plus massifs ; ceci met en évidence un autre aspect : la masse “pesante”, a priori différence de la masse “inerte”.

L’identité de la masse pesante et de la masse inerte n’est pas évidente, mais c’est une constatation expérimentale (d’où découle la relativité générale).

• On pose alors par définition que deux masses sont égales si et seulement si, l’équilibre d’une balance étant obtenu avec l’une des masses, il est conservé quand on y remplace cette masse par l’autre.

Depuis 1901, on avait ainsi défini un étalon de masse “kilogramme” (cylindre de platine iridié ; précision

≈{10}^{-9}

) ; depuis mai 2019, l'unité de masse se déduit de celle d'énergie par la relation

E=m \:c^2

où

c=299 \,792 \,458 \:\mathrm{m.s^{-1}}

est considérée comme une valeur exacte (précision relative

{10}^{-14}

).

◊ remarque : l'unité d'énergie est elle même déduite de celle de temps par la relation de Planck

E=h \:ν

avec

h=6\text{,}62607015.{10}^{-34} \: \mathrm{J.s}

considérée comme une valeur exacte (précision relative

{10}^{-14}

Principe d’inertie et référentiels galiléens

• Deux systèmes sont en “interaction” s’il existe une modification de l’un qui cause une modification de l’autre. Un système “isolé” n’a pas d'interaction.

En pratique, il n’existe pas de système “isolé”, à part l’Univers en entier ; mais on constate que les interactions semblent tendre vers zéro à grande distance : les systèmes très éloignés sont donc supposés “quasi-isolés”.

◊ remarque : au niveau microscopique, il est impossible d’observer un système strictement isolé car l'observation est une interaction non négligeable.

• Le “principe de l’inertie” suppose qu’il existe des référentiels dans lesquels le mouvement de tout point matériel isolé est rectiligne et uniforme ; on les appelle “référentiels d’inertie” ou “référentiels galiléens”.

• Un référentiel lié à la Terre est approximativement galiléen pour de nombreuses expériences ; par contre il ne l’est pas pour l’étude d’un mouvement dépendant de la rotation de la Terre sur elle même.

Le référentiel de Copernic est “mieux” galiléen : centré au barycentre du système solaire et orienté par rapport à des étoiles lointaines (pour que leur mouvement soit négligeable par effet de “perspective”). Il est toutefois insuffisant pour l’étude d’un mouvement dépendant de la rotation de la galaxie…

• Si un référentiel est galiléen, alors tous les référentiels animés par rapport à lui d’un mouvement rectiligne et uniforme sont aussi galiléens (d’après la loi de composition des vitesses) ; inversement, tous les référentiels animés par rapport à lui d’un mouvement accéléré sont non galiléens.

Principe fondamental de la dynamique

Quantité de mouvement

• Pour un système de deux points matériels

A

B

, on peut définir un centre de masse

G

par la relation :

(m_A+m_B ) \: \overset{⟶}{OG}=m_A \: \overset{⟶}{OA}+m_B \: \overset{⟶}{OB}

.

Pour un tel système isolé, on vérifie expérimentalement, dans tout référentiel galiléen, la conservation de la quantité :

(m_A+m_B ) \: \overset{→}{v}_G=m_A \: \overset{→}{v}_A+m_B \: \overset{→}{v}_B

Ceci conduit à considérer que la grandeur importante pour décrire le mouvement des points matériels (c'est-à-dire la “dynamique”) n’est pas la vitesse mais la “quantité de mouvement” (ou “impulsion”) :

\overset{→}{p}=m \:\overset{→}{v}

◊ remarque : ces relations ne sont plus valables en mécanique relativiste.

Forces

• Dans un référentiel galiléen, si un point matériel a un mouvement rectiligne et uniforme, c’est soit qu’il est isolé, soit qu’il est soumis à plusieurs interactions qui se compensent (“pseudo-isolé”).

Si au contraire il a un mouvement non rectiligne ou non uniforme (vitesse non constante, accélération non nulle), on peut considérer qu’il est soumis à une interaction (ou plusieurs interactions qui ne se compensent pas).

• Les interactions peuvent alors être décrites par des quantités vectorielles : les forces. Le rôle important de la quantité de mouvement conduit à définir celles-ci d’après les variations de

\overset{→}{p}

(plutôt que celles de

\overset{→}{v}

) :

$\displaystyle ∑ \overset{→}{F} =\frac{d\overset{→}{p}}{dt}$ (“principe fondamental” de la dynamique ; PFD).

◊ remarque : puisque la masse est constante :

\displaystyle ∑ \overset{→}{F} =m \: \frac{d\overset{→}{v}}{dt}=m\: \overset{→}{a}

, mais cette relation n’est plus valable en mécanique relativiste.

◊ remarque : pour un système de points, des forces peuvent aussi causer des rotations ou des déformations (mais c’est impossible pour un point).

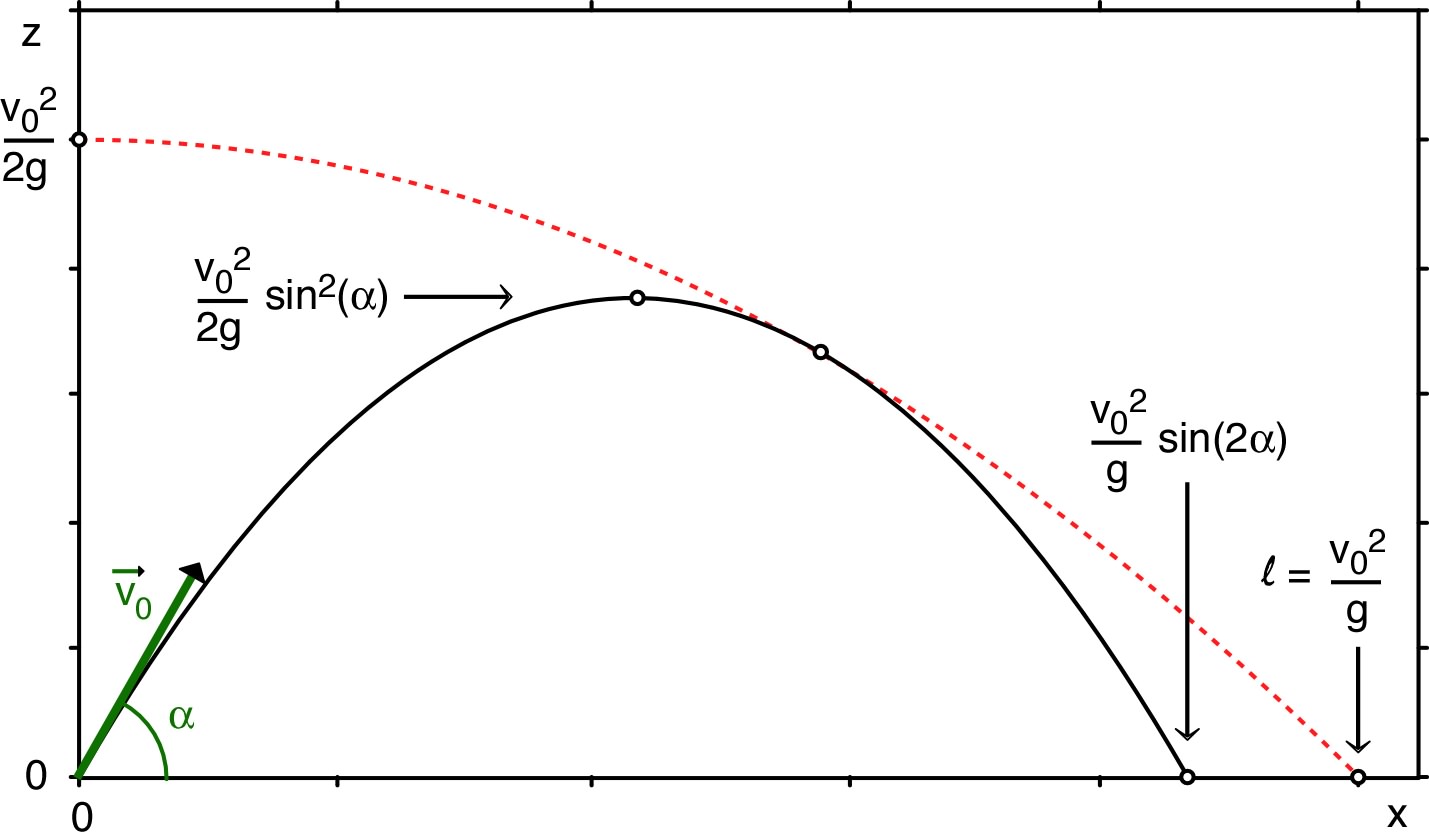
Exemple d’application : tir d’un projectile

• En première approximation, on peut souvent négliger le frottement sur l’air : le projectile (représenté par son centre d’inertie, point matériel) est alors soumis uniquement à la pesanteur :

\overset{→}{P}=m \:\overset{→}{g}=m \:\overset{→}{a}

.

En supposant

\overset{→}{g}

uniforme, on obtient alors compte tenu des conditions initiales :

\overset{→}{a}=\dot{\overset{→}{v}}=\overset{→}{g}

;

\overset{→}{v}=\dot{\overset{⟶}{OM}}=\overset{→}{g} \: t+\overset{→}{v}_0

;

\overset{⟶}{OM}=\frac{1}{2} \overset{→}{g} \: t^2+\overset{→}{v}_0 \: t+\overset{⟶}{OM}_0

Ainsi, par différentes combinaisons des équations en projection :

l’équation de la trajectoire est : $\displaystyle z=-\frac{g}{2 \,v_0^{\:2} \: \cos^2(α)} \:x^2+x \: \tan(α)$ ;
l’équation de la “parabole de sûreté” est : $\displaystyle z=-\frac{g}{2 \,v_0^{\:2}} \: x^2+\frac{v_0^{\:2}}{2 \,g}$ ;
l’altitude maximum atteinte est : $\displaystyle z_{max}=\frac{v_0^{\:2}}{2 \,g} \: \sin^2(α)$ ;
la “portée” est : $\displaystyle x_{max}=\frac{v_0^{\:2}}{g} \: \sin(2 \,α)$ (en trajectoire “rasante” ou “plongeante”) ; la portée maximum est : $\displaystyle 𝓁=\frac{v_0^{\:2}}{g}$ (pour $α=\frac{π}{4}$ ).

📖 exercices n° I et II.

Principe des actions réciproques

• Toute interaction correspond à deux actions réciproques ; l’étude complète dépasse donc l’étude d’un point matériel, mais certains aspects en sont utiles pour calculer les forces exercées sur le point étudié.

• Si on considère un système de deux points matériels qui interagissent entre eux mais tels que l’ensemble est isolé, alors pour le système :

\overset{→}{p}=\overset{→}{p}_A+\overset{→}{p}_B

est un vecteur constant ; par suite :

\overset{→}{F}_{A→B}+\overset{→}{F}_{B→A}=\overset{→}{0}

Ceci peut se généraliser en un “principe des actions réciproques”, qui est valable dans de très nombreux cas :

\overset{→}{F}_{A→B}=-\overset{→}{F}_{B→A}

◊ remarque : en mécanique quantique, les interactions sont décrites par des “champs” qui se propagent ; avec les délais de propagation, ce principe n’est alors applicable que dans un sens beaucoup plus restreint.

Principe de relativité de Galilée

• Le principe “fondamental”

\displaystyle ∑ \overset{→}{F} =\frac{d\overset{→}{p}}{dt}

n’est lié qu’à la variation de vitesse, donc il s’exprime de la même manière dans deux référentiels galiléens, animés l’un par rapport à l’autre d’un mouvement rectiligne et uniforme.

Cela dépend en fait des hypothèses : de

\overset{⟶}{OM}=\overset{⟶}{O'M}+\overset{→}{v}_e \: t

et aussi

t'=t

on déduit :

\displaystyle ∑ \overset{→}{F} =m \:\ddot{\overset{⟶}{OM}}=m \:\ddot{\overset{⟶}{O'M}}=∑ \overset{→}{F}{}'

.

On peut exprimer ceci comme “principe de relativité de Galilée” : les lois de la mécanique sont invariantes lors du passage d’un référentiel galiléen à un autre référentiel galiléen.

◊ remarque : pour l’étude de la propagation de la lumière, on constate que ce principe est en contradiction avec l’expérience ; il faut alors adopter le principe de relativité d’Einstein, basé sur d’autres hypothèses (“relativistes”, avec entre autres

t'≠t

), qui généralise l’invariance à toutes les lois physiques.