DYNAMIQUE - PRINCIPE FONDAMENTAL - corrigé des exercices

Tir dans le vide

• La relation fondamentale de la dynamique de translation peut s’écrire :

m \:\overset{→}{a}=\overset{→}{P}=m \:\overset{→}{g}

puisqu’on néglige les autres effets.
• Compte tenu des conditions initiales, une première intégration donne :

\overset{→}{v}(t)=\overset{→}{g} \: t+\overset{→}{v}_0

; une seconde intégration donne :

\overset{⟶}{OM}=\frac{1}{2} \overset{→}{g} \: t^2+\overset{→}{v}_0 \: t+\overset{⟶}{OM}_0

.
• Le mouvement est en entier dans le plan vertical défini par la position

M_0

et les directions de

\overset{→}{v}_0

\overset{→}{g}

; on peut donc raisonner avec deux coordonnées

x

z

dans ce plan.
• Si on prend

M_0

comme origine, on cherche à obtenir :

x=v_{0x} \: t=v_0 \: \cos(α) \: t

maximum (où

α

est l’angle de

\overset{→}{v}_0

avec l’horizontale), tout en imposant :

z=v_{0z} \: t-\frac{1}{2} g \:t^2=v_0 \: \sin(α) \: t-\frac{1}{2} g \:t^2=h

. Aucune condition n’étant imposée sur la durée du trajet, seule la trajectoire importe et on peut obtenir son équation en éliminant

t

\displaystyle z(x)=\tan(α) \: x-\frac{g}{2 \,v_0^{\:2} \: \cos^2(α)} \, x^2=\tan(α) \: x-\left[1+\tan^2(α) \right] \, \frac{g}{2 \,v_0^{\:2}} \: x^2=h

. Le maximum

x_m

est alors obtenu en choisissant la valeur de

α

la plus efficace.
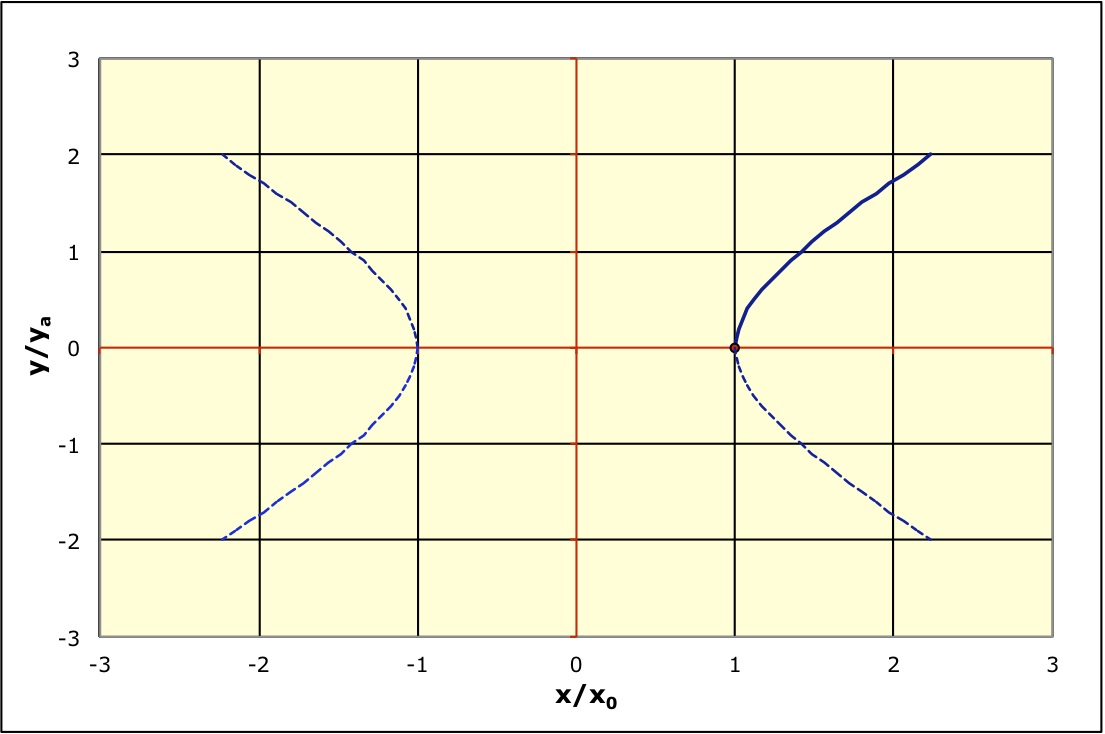
• On peut ensuite considérer que si, pour

x

fixé, on pouvait ajuster

α

afin d’atteindre

z(x)>h

, alors (puisque le point

M

finit toujours par retomber) il serait forcément possible d’atteindre

z(x'\,)=h

avec un

x'>x

. Autrement dit : pour

x=x_m

le point d’altitude

z(x_m)=h

se trouve forcément sur la parabole du sûreté (le plus haut qu’il est possible d’atteindre en ajustant

α

pour

x=x_m

donné).
◊ remarque : cette “équivalence” simplifie beaucoup le calcul car il est plus facile de chercher l’extremum de

z

pour

x

fixé (l’équation de la trajectoire est quadratique en

x

et linéaire en

z

).
• Pour établir l'équation de la courbe de sûreté, on peut commencer par simplifier les notations en posant (par exemple) :

λ=\tan(α)

\displaystyle μ=\frac{g}{v_0^{\:2}}

; on obtient ainsi :

\displaystyle z=λ \:x-\left(1+λ^2 \right) \: \frac{μ}{2} \, x^2

.
• Pour chercher le maximum, on peut ensuite dériver cette relation par rapport à

λ

(cela revient au même que de dériver par rapport à

α

) en considérant

x

fixé :

\displaystyle 0=\frac{dz}{dλ}=x-λ \:μ \:x^2

.
• Le maximum cherché est tel que

\displaystyle \frac{dz}{dλ}=0

c’est-à-dire :

\displaystyle λ \:x=\frac{1}{μ}

. Il suffit alors de remplacer dans l’expression de

z

\displaystyle z_m (x)=λ \:x-\left(1+λ^2 \right) \: \frac{μ}{2} \: x^2=\frac{1-μ^2 \: x^2}{2 \,μ}

(c'est l’équation de la parabole de sûreté).
• Inversement, en imposant dans cette équation

z_m (x_m)=h

, on obtient :

$\displaystyle x_m=\frac{\sqrt{1-2 \,μ \:h}}{μ}=\frac{v_0^{\:2}}{g} \: \sqrt{1-\frac{2 \,g \:h}{v_0^{\:2}}}≈2900 \:\mathrm{m}$ .

◊ remarque : en négligeant les frottements sur l’air, la précision est médiocre pour une telle distance.
◊ remarque : on obtient aussi :

\displaystyle λ_m=\frac{1}{μ \:x_m}=\frac{1}{\sqrt{1-\frac{2 \,g \:h}{v_0^{\:2}}}}=1\text{,}4=\tan(α_m )

α_m≈54°=0\text{,}95 \:\mathrm{rad}

• On cherche maintenant à obtenir :

\displaystyle z_m \left(\frac{x_m}{2}\right)=h

(en supposant qu’en plaçant la nouvelle origine à une distance

\displaystyle \frac{x_m}{2}

on garde l’altitude

z=0

) ; ceci donne

\displaystyle λ \: \frac{x_m}{2}-(1+λ^2 ) \: \frac{μ}{8} \: x_m^{\:2}=h

d’où on déduit :

$\displaystyle λ_1=\frac{2 \,-\sqrt{4-μ .(μ \,x_m^{\:2}+8 \,h)}}{μ \,x_m}=1\text{,}07$ et $α_1≈47°=0\text{,}82 \:\mathrm{rad}$ (éventuel tir tendu) ;
$\displaystyle λ_2=\frac{2 \,+\sqrt{4-μ .(μ \,x_m^{\:2}+8 \,h)}}{μ \,x_m}=4\text{,}55$ et $α_2≈78°=1\text{,}35 \:\mathrm{rad}$ (tir en cloche).

◊ remarque : le tir tendu n'est possible que si l'obus peut arriver par dessous.

• La vitesse de l’obus quand il touche l’objectif peut se calculer en dérivant les coordonnées, puis en calculant l’instant de l’impact pour en déduire les coordonnées de la vitesse et sa norme. Mais on peut plus simplement utiliser le théorème de l’énergie cinétique ou la conservation de l’énergie mécanique, d’où on déduit :

v=\sqrt{v_0^{\:2}-2 \,g \:h}=143 \:\mathrm{m.s^{-1}}

Recherche de trajectoire

1.a.	• Le principe fondamental de la dynamique de translation peut s’écrire : $m \:\overset{→}{a}=k \:\overset{⟶}{OM}$ ou encore : $\ddot{\overset{⟶}{OM}}-λ^2 \: \overset{⟶}{OM}=\overset{→}{0}$ en posant $\displaystyle λ=\sqrt{\frac{k}{m}}$ . • Une telle équation différentielle du second ordre est linéaire (sans second membre) et peut s’intégrer (par exemple) à l’aide des coordonnées cartésiennes : $\ddot{x}-λ^2 \: x=0$ ; $\ddot{y}-λ^2 \: y=0$ ; $\ddot{z}-λ^2 \: z=0$ . • L’équation sur $x$ a pour solution générale : $x=A \:\mathrm{e}^{λ \,t}+B \:\mathrm{e}^{-λ \,t}$ , donnant $\dot{x}=λ \:A \:\mathrm{e}^{λ \,t}-λ \:B \:\mathrm{e}^{-λ \,t}$ . La condition initiale $\dot{x}(0)=0$ impose $A=B$ ; la condition initiale $x(0)=x_0$ donne $\displaystyle A=B=\frac{x_0}{2}$ c’est-à-dire : $\displaystyle x=\frac{x_0}{2} \, \left(\mathrm{e}^{λ \,t}+\mathrm{e}^{-λ \,t} \right)=x_0 \: \cosh(λ \,t)$ . • L’équation sur y donne de même : $y=A \:\mathrm{e}^{λ \,t}+B \:\mathrm{e}^{-λ \,t}$ avec $\dot{y}=λ \:A \:\mathrm{e}^{λ \,t}-λ \:B \:\mathrm{e}^{-λ \,t}$ . La condition initiale $y(0)=0$ impose $A=-B$ ; la condition initiale $\dot{y}(0)=v_0$ donne $\displaystyle A=-B=\frac{v_0}{2 \,λ}$ c’est-à-dire : $\displaystyle y=\frac{v_0}{2 \,λ} \, \left(\mathrm{e}^{λ \,t}-\mathrm{e}^{-λ \,t} \right)=\frac{v_0}{λ} \: \sinh(λ \,t)$ . • L’équation sur z donne de même : $z=A \:\mathrm{e}^{λ \,t}+B \:\mathrm{e}^{-λ \,t}$ avec $\dot{z}=λ \:A \:\mathrm{e}^{λ \,t}-λ \:B \:\mathrm{e}^{-λ \,t}$ . La condition initiale $\dot{z}(0)=0$ impose $A=B$ ; la condition initiale $z(0)=0$ donne $A=B=0$ donc $z=0$ .

1.b.	• La relation $z=0$ montre que le mouvement s'effectue dans le plan $Oxy$ (les mouvements à accélération radiale sont contenus dans le plan déterminé par les conditions initiales).

2.a.	• Les équations de la trajectoire sont $z=0$ et l’équation obtenue en éliminant $t$ entre $x(t)$ et $y(t)$ dans le plan $Oxy$ (correspondant à $z=0$ ). • Si on n’est pas familier des fonctions “hyperboliques” $\cosh$ et $\sinh$ , on peut simplifier les notations : $Λ=\mathrm{e}^{λ \,t}$ ; $\displaystyle ξ=\frac{2 \,x}{x_0} =Λ+\frac{1}{Λ}$ et $\displaystyle η=\frac{2 \,λ \:y}{v_0} =Λ-\frac{1}{Λ}$ . Ceci donne : $\displaystyle Λ=\frac{ξ+η}{2}$ et $\displaystyle Λ=\frac{2}{ξ-η}$ ; $ξ^2-η^2=4$ ; $\displaystyle \left(\frac{x}{x_0} \right)^2-\left(\frac{λ \:y}{v_0} \right)^2=1$ .

2.b.	• L'allure de la trajectoire est la suivante : • C'est une hyperbole, dont les sommets (sur l’axe des $x$ ) ont pour abscisses $x=±x_0$ et dont les asymptotes (obliques) ont pour équations : $\displaystyle \frac{y}{y_a} =±\frac{x}{x_0}$ (en posant $\displaystyle y_a=\frac{v_0}{λ}$ ). La trajectoire est la branche d’hyperbole passant par $x=x_0$ .

3.a.	• Le principe fondamental de la dynamique de translation peut s’écrire : $m \:\overset{→}{a}=-k \:\overset{⟶}{OM}$ ou encore : $\ddot{\overset{⟶}{OM}}+ω^2 \: \overset{⟶}{OM}=\overset{→}{0}$ en posant $\displaystyle ω=\sqrt{\frac{k}{m}}$ (il s’agit ici d’une force attractive). • Une telle équation différentielle peut s’intégrer (par exemple) à l’aide des coordonnées cartésiennes : $\ddot{x}+ω^2 \: x=0$ ; $\ddot{y}+ω^2 \: y=0$ ; $\ddot{z}+ω^2 \: z=0$ . • L’équation sur $x$ donne : $x=A \: \cos(ω \,t)+B \: \sin(ω \,t)$ avec $\dot{x}=-ω \:A \: \sin(ω \,t)+ω \:B \: \cos(ω \,t)$ . La condition initiale $\dot{x}(0)=0$ impose $B=0$ ; la condition initiale $x(0)=x_0$ donne $A=x_0$ c’est-à-dire : $x=x_0 \: \cos(ω \,t)$ . • L’équation sur $y$ donne : $x=A \: \cos(ω \,t)+B \: \sin(ω \,t)$ avec $\dot{y}=-ω \:A \: \sin(ω \,t)+ω \:B \: \cos(ω \,t)$ . La condition initiale $y(0)=0$ impose $A=0$ ; la condition initiale $\dot{y}(0)=v_0$ impose $\displaystyle B=\frac{v_0}{ω}$ c’est-à-dire : $\displaystyle y=\frac{v_0}{ω} \: \sin(ω \,t)$ . • L’équation sur $z$ donne : $x=A \: \cos(ω \,t)+B \: \sin(ω \,t)$ avec $\dot{z}=-ω \:A \: \sin(ω \,t)+ω \:B \: \cos(ω \,t)$ . La condition initiale $\dot{z}(0)=0$ impose $B=0$ ; la condition initiale $z(0)=0$ impose $A=0$ c’est-à-dire : $z=0$ (les mouvements à accélération radiale restent dans le plan déterminé par les conditions initiales...). • Les équations de la trajectoire sont $z=0$ et l’équation obtenue en éliminant $t$ entre $x(t)$ et $y(t)$ dans le plan $Oxy$ (correspondant à $z=0$ ) : $\left(\frac{x}{x_0} \right)^2-\left(\frac{ω \:y}{v_0} \right)^2=1$ . • L'allure de la trajectoire est la suivante : • C'est une ellipse, dont les sommets sur l’axe des $x$ ont pour abscisses $x=±x_0$ et dont les sommets sur l’axe des $y$ ont pour abscisses $y=± y_a$ (en posant $\displaystyle y_a=\frac{v_0}{ω}$ ).

3.b.	• La différence essentielle avec le mouvement précédent est que les trajectoires sont fermées et que le mouvement est périodique (la conservation de l'énergie impose que si le mobile revient à la même position, c'est avec la même vitesse, dont il continue de même qu'initialement).