M. II - DYNAMIQUE ; FORCES

Différents types de forces

• L'application du principe de la dynamique nécessite d'établir un bilan des forces ; certaines peuvent être décrites par des “actions à distance” :

force de gravitation (pesanteur) ; grande portée, mais faible ;
forces électro-faibles :
- électromagnétiques ; grande portée, compensation des + et - ;
- nucléaires faibles ; courte portée ;
forces nucléaires fortes ; très fortes, mais courte portée.

À notre échelle, certaines forces (électriques au niveau microscopique) sont bien décrites par des “actions de contact” (portée apparente “nulle”).

Forces de contact dans un fluide

Caractéristiques générales

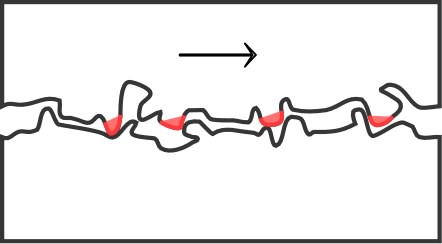
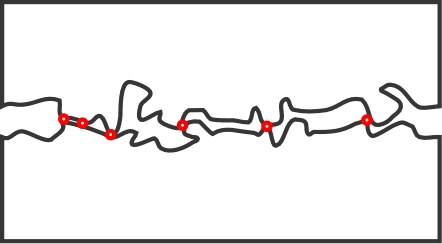
• Sur chaque “élément de surface” d’un objet au contact d’un fluide (liquide ou gaz), la “force de contact” peut être décrite en deux composantes :

une force pressante (normale) ;
un frottement (tangentiel).

◊ remarque : certains systèmes (par exemples les bulles) peuvent être décrits par des forces tangentielles de “tension superficielle” (forces de “capillarité”), non étudiées ici.

• À l'équilibre, il n'y a généralement pas de frottement ; la résultante des forces pressantes sur l’ensemble de l’objet est la poussée d’Archimède. Cette force est égale à l’opposé du poids du fluide “déplacé” par l’objet.

◊ remarque : certains “fluides pâteux” (peintures, suspensions de poudre solide dans un fluide) peuvent comporter un frottement non nul à l'équilibre.

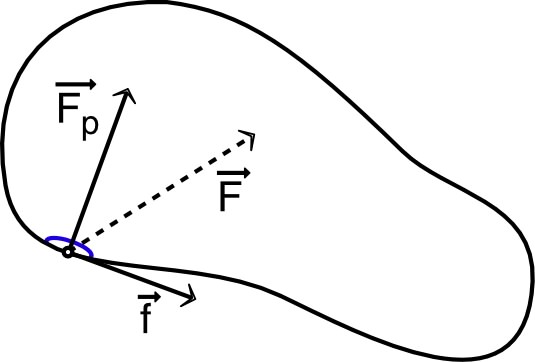
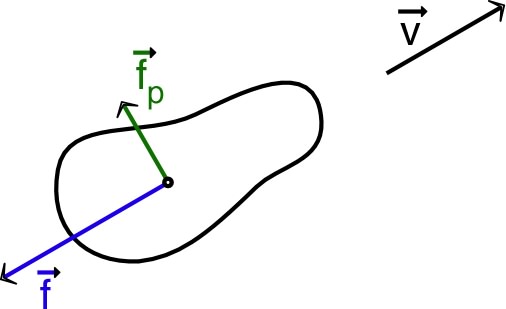
• Pour un objet en mouvement dans un fluide, la résultante des forces de contact sur l’ensemble de sa surface n'est pas simple à calculer.

On peut souvent la décrire en ajoutant :

une force de traînée cinématique (souvent nommée à tort “frottement”), parallèle et de sens contraire au mouvement relatif ( $\overset{→}{v}_{rel}=\overset{→}{v}-\overset{→}{v}_{fl.}$ ) ;
une force de portance, perpendiculaire au mouvement relatif.

La traînée cinématique (“frottement”) est en première approximation :

proportionnelle à la vitesse pour les faibles vitesses (régime “visqueux”, ou “laminaire”) : $\overset{→}{f}=-k' \;\overset{→}{v}_{rel}$ ;
proportionnelle au carré de la vitesse pour les plus grandes vitesses (régime “turbulent”) : $\overset{→}{f}=-k'' \:v_{rel} \; \overset{→}{v}_{rel}$ .

• Pour un objet accéléré dans un fluide, il s'ajoute aussi un effet de traînée dynamique, environ proportionnelle et de sens contraire à l'accélération.

◊ remarque : cet effet est souvent négligé mais n'est pas toujours négligeable.

Lancer avec frottement fluide laminaire

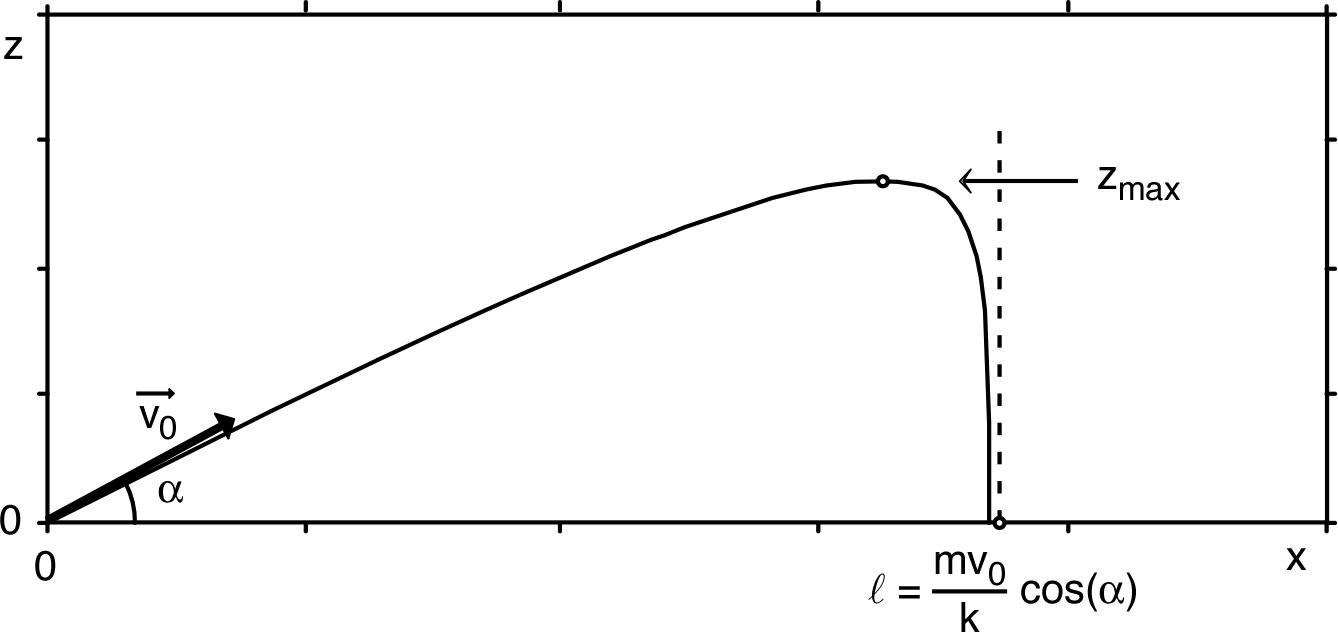
• On considère le lancer d’un projectile :

\displaystyle \overset{→}{P}+\overset{→}{f}=m \, \frac{d\overset{→}{v}}{dt}

avec un frottement sur l’air proportionnel à la vitesse (faible) :

\overset{→}{f}=-k \;\overset{→}{v}

.

• Pour

\overset{→}{g}

uniforme, on obtient l’équation linéaire :

\displaystyle \frac{d\overset{→}{v}}{dt}+\frac{k}{m} \, \overset{→}{v}=\overset{→}{g}

. Une solution particulière est :

\displaystyle \overset{→}{v}=\frac{m}{k} \, \overset{→}{g}

; la solution générale de l’équation homogène est :

\overset{→}{v}=\overset{→}{A} \: \mathrm{e}^{-kt/m}

où

\overset{→}{A}∈ℝ^3

est une constante d’intégration.

D’après les conditions initiales :

\displaystyle \overset{→}{v}=\overset{→}{v}_0 \; \mathrm{e}^{-kt/m}+\frac{m}{k} \, \overset{→}{g} .\left(1-\mathrm{e}^{-kt/m} \right)

; donc (avec

\overset{⟶}{OM}_0=\overset{→}{0}

) :

\displaystyle \overset{⟶}{OM}=\frac{m}{k} \,\left(\overset{→}{v}_0-\frac{m}{k} \, \overset{→}{g} \right)\left(1-\mathrm{e}^{-kt/m} \right)+\frac{m}{k} \, \overset{→}{g} \: t

• On peut ainsi en déduire :

l’altitude maximum : $\displaystyle z_{max}=\frac{m}{k} \, v_0 \; \sin(α)-\frac{m^2 \: g}{k^2} \, \ln\left(1+\frac{k \:v_0 \; \sin(α)}{m \:g}\right)$ ;
la portée “limite” : $\displaystyle 𝓁=\frac{m}{k} \, v_0 \; \cos(α)$ (presque atteinte si $k \:v_0≫m \:g$ ).

📖 exercices n° I et II.

Forces de contact entre solides

Caractéristiques générales (loi de Coulomb)

• Sur chaque élément de surface, la “force de contact” peut être décrite par une force pressante (normale) et un frottement (tangentiel).

• Pour deux solides en contact, la résultante des forces pressantes sur une portion de la surface de contact est souvent appelée “réaction normale”.

Par l’effet d’élasticité microscopique des solides, cette force s’adapte à la valeur juste nécessaire pour empêcher la traversée mutuelle des solides.

• Quand il n’y a pas de glissement, le frottement “solide” s’adapte (en direction, sens et norme) à la valeur juste nécessaire à éviter le glissement.

Ceci peut généralement être modélisé par l'interaction des aspérités, éventuellement microscopiques (1). Mais quand la taille des aspérités devient de l'ordre de grandeur de la dimension atomique, certains aspects du frottement peuvent devenir différents (2).

(1)

Les aspérités emboîtées s'opposent au déplacement.

La limite de glissement est atteinte quand la déformation des aspérités permet le déplacement.

L'accroissement de la réaction normale augmente les déformations nécessaires au glissement.

(2)

Des atomes des aspérités en contact se lient, s'opposant ainsi au déplacement.

La limite de glissement est atteinte quand les liaisons se rompent (avec déformation des aspérités).

L'accroissement de la réaction normale augmente le nombre de liaisons (“adhésion”).

La limite de glissement correspond à un frottement maximum proportionnel à la réaction normale :

f_{max}=λ_0 \: R

avec un coefficient

λ_0

qui dépend :

de la rugosité de surface ;
de l’élasticité microscopique ;
de l’adhésion à l'échelle atomique.

◊ remarque : la rugosité augmente généralement le frottement si plus d'aspérités s’accrochent, mais la rugosité à l'échelle atomique diminue le frottement s’il y a moins de points d’adhésion.

◊ remarque : pour des surfaces “lisses” usuelles, la surface de contact réelle est moins de

0\text{,}01 \:%

de la surface de contact apparente.

• Quand il y a glissement, le frottement est opposé au sens du mouvement (relatif) et de norme inférieure mais voisine du frottement maximum :

f=λ \:R

avec

λ≤λ_0

(et souvent

λ≈λ_0

◊ remarque : le frottement de glissement dépend des vibrations associées aux “accrochages-décrochages” au niveau des aspérités (le frottement est fort s’il se produit des vibrations correspondant à une fréquence de résonance des solides en contact).

◊ remarque : en présence d’un lubrifiant, le frottement limite sans glissement est en général nettement diminué, par ailleurs la norme du frottement avec glissement peut dépendre de la vitesse.

Glissement d’un point sur une surface

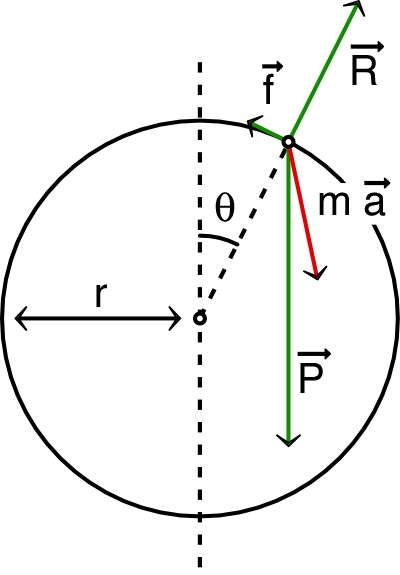
• On étudie le mouvement d’un point, mobile sur une sphère de rayon

r

, lâché près du sommet avec une vitesse initiale nulle ; ce point est alors soumis à : son poids

\overset{→}{P}

; la réaction normale

\overset{→}{R}

; le frottement

\overset{→}{f}

.

Le principe fondamental de la dynamique peut s'écrire :

\overset{→}{P}+\overset{→}{R}+\overset{→}{f}=m \:\overset{→}{a}

.

• Compte tenu de la géométrie de l'expérience, le mouvement est dans un plan vertical. En effet,

\overset{→}{P}

est vertical et

\overset{→}{R}

radiale ; en outre :

initialement $\overset{→}{f}$ est parallèle et de sens contraire à la projection tangentielle de $\overset{→}{P}$ , c’est-à-dire dans le même plan vertical, qui est donc celui dans lequel le mouvement débute ;
ensuite $\overset{→}{f}$ est parallèle à la vitesse, c’est-à-dire dans le même plan vertical, qui est donc celui dans lequel le mouvement se poursuit.

En coordonnées polaires, avec

θ

mesuré à partir de la verticale, on obtient (lors du mouvement) :

$\overset{→}{R}=R \;\overset{→}{u}_r$ ; $\overset{→}{f}=-f \;\overset{→}{u}_θ$ ;
$\overset{→}{P}=-m \:g \; \cos(θ) \; \overset{→}{u}_r+m \:g \; \sin(θ) \; \overset{→}{u}_θ$ ;
$\overset{→}{v}=r \:\dot{θ} \; \overset{→}{u}_θ$ ; $\overset{→}{a}=-r \:\dot{θ}^2 \: \overset{→}{u}_r+r \:\ddot{θ} \; \overset{→}{u}_θ$ .

On aboutit ainsi aux deux équations :

$m \:r \:\ddot{θ}=m \:g \; \sin(θ)-f$ ; (1)

$R=m \:g \; \cos(θ)-m \:r \:\dot{θ}^2$ ; (2)

liées par la condition :

f=λ \:R

(dépendant de

θ

• L’hypothèse du mouvement suppose toutefois que le frottement initial n’est pas trop grand :

m \:g \; \sin(θ_0 )-f_0>0

(où

θ_0>0

est un décalage indispensable pour que le point ne soit pas en équilibre au voisinage du sommet).

• Dans l'équation (1) :

f(θ)=λ \:R(θ)=λ \:m .\left[g \:\cos(θ) - r \:\dot{θ}^2 \,\right]

et donc :

$r \:\ddot{θ}-λ \:r \:\dot{θ}^2=g \; \sin(θ)-λ \:g \; \cos(θ)$ (3).

Le glissement initial correspond à

\ddot{θ}(0)>0

avec

\dot{θ}(0)=0

, d'où on déduit :

θ_0>\arctan(λ)≈10°

pour une surface usuelle “peu rugueuse”.

• L'équation différentielle (3) ne peut s’intégrer simplement que dans le cas particulier, d'un intérêt limité, où

λ≈0

(frottement négligeable).

Dans ce cas, en multipliant par

\dot{θ}

m \:r \:\dot{θ} \: \ddot{θ}=m \:g \; \sin(θ) \: \dot{θ}

d’où on déduit, vu les conditions initiales :

m \:r \:\dot{θ}^2 = 2 \,m \:g .[cos⁡(θ_0 ) - cos⁡(θ) ]

; cette relation décrit la conservation de l'énergie mécanique.

◊ remarque : la seconde intégration ne peut pas se faire simplement.

• L'équation (2) peut alors s’écrire (pour

λ≈0

) :

$R=m \:g .[3 \, \cos(θ)-2 \,\cos(θ_0 ) ]$ ;

ceci donne, dans le cas particulier

θ_0≈0

(frottement négligeable) :

$R=m \:g .[3 \, \cos(θ)-2]$ .

La condition de contact (

R≥0

) impose :

θ≤\arccos\left(\frac{2}{3}\right)≈0\text{,}84 \:\mathrm{rad}≈48°

. Le point quitte ensuite la surface et continue en chute libre parabolique.

◊ remarque : le contact est dans ce cas “unilatéral” : la traversée est impossible mais la séparation est possible d’un côté (par contre, pour un anneau coulissant le long d’un fil, la liaison serait multilatérale).