DYNAMIQUE - FORCES - corrigé des exercices

A. EXERCICES DE BASE

Frottement proportionnel à la vitesse

1.a.	• La relation fondamentale de la dynamique de translation peut s’écrire : $m \:\overset{→}{a}=\overset{→}{F}=-k \:\overset{→}{v}$ . On en déduit que tout le mouvement se fait suivant la direction et le sens de la vitesse initiale et qu’algébriquement : $\dot{v}=-λ \:v$ ; par suite, compte tenu des conditions initiales : $v=v_0 \: \mathrm{e}^{-λt}$ . • La distance parcourue en une durée $t$ est : $\displaystyle x(t)=∫_0^t v(t') \: dt'=∫_0^t v_0 \: \mathrm{e}^{-λt'} \: dt'=\frac{v_0}{λ} \left(1-\mathrm{e}^{-λt} \right)$ .

1.b.	• La distance totale que peut parcourir le point est : $\displaystyle D=∫_0^∞ v(t) \: dt=\frac{v_0}{λ}$ donc : $\displaystyle λ=\frac{v_0}{D}=0\text{,}02 \:\mathrm{s^{-1}}$ .

• D’une façon analogue :

\displaystyle 𝓁_i=∫_0^{t_i} v(t) \: dt=\frac{v_0}{λ} \, \left(1-\mathrm{e}^{-λt_i} \right)

t_i=-\frac{\ln\left(1-\frac{λ \:𝓁_i}{v_0} \right)}{λ}=-\frac{\ln\left(1-\frac{𝓁_i}{D}\right)}{λ}

.
• L’application numérique donne :

t_1=34\text{,}6 \:\mathrm{s}

;

t_2=230 \:\mathrm{s}

• Puisque la force n'est pas constante, il faut calculer le travail infinitésimal sur un petit déplacement élémentaire, puis intégrer sur le déplacement total.
• D’après :

dW=\overset{→}{F}⋅d\overset{⟶}{OM}=-k \:\overset{→}{v}⋅\overset{→}{v} \: dt=-k \:v_0^{\:2} \: \mathrm{e}^{-2λt} \: dt

on obtient :

$\displaystyle W_i=∫_0^{t_i} -k \:v_0^{\:2} \: \mathrm{e}^{-2λt} \: dt=\frac{1}{2} m \:v_0^{\:2} \: \left(\mathrm{e}^{-2λt_i}-1\right)$ .

◊ remarque : on retrouve le théorème de l’énergie cinétique.
• L’application numérique donne :

W_1=-1\text{,}50 \:\mathrm{mJ}

;

W_2=-1\text{,}9998 \:\mathrm{mJ}≈-2\text{,}00 \:\mathrm{mJ}

(le travail limite n’est pas encore atteint, mais la différence est inférieure à l’incertitude de mesure).
◊ remarque :

W_i<0

car le travail du frottement est résistant.

Frottement proportionnel au carré de la vitesse

1.a.	• La relation fondamentale de la dynamique de translation peut s’écrire : $m \:\overset{→}{a}=\overset{→}{F}=-k \:v \:\overset{→}{v}$ . On en déduit que tout le mouvement se fait suivant la direction et le sens de la vitesse initiale et qu’algébriquement : $\dot{v}=-λ \:v^2$ c'est-à-dire : $\displaystyle \frac{dv}{v^2} =-λ \:dt$ . • Compte tenu des conditions initiales, on en obtient : $\displaystyle \frac{1}{v}=\frac{1}{v_0} +λ \:t$ puis $\displaystyle v(t)=\frac{v_0}{1+v_0 \: λ \:t}$ . • La distance parcourue en une durée $t$ est : $\displaystyle x(t)=∫_0^t v(t') \: dt'=∫_0^t \frac{v_0}{1+v_0 \: λ \:t'} \: dt'=\frac{\ln(1+v_0 \: λ \:t)}{λ}$ .

1.b.	• La distance $D$ parcourue par le point est : $\displaystyle D=∫_0^T v(t) \: dt=∫_0^T \frac{v_0}{1+v_0 \: λ \:t} \: dt=\frac{\ln(1+v_0 \: λ \:T)}{λ}$ . • Il est impossible d’expliciter $λ$ à partir de cette relation, mais on peut par exemple résoudre implicitement par approximations successives. En partant de $\displaystyle λ_0=\frac{1}{v_0 \: T}=0\text{,}010 \:\mathrm{m^{-1}}$ (ordre de grandeur raisonnable) au numérateur, on obtient : $\displaystyle λ_1=\frac{\ln(2)}{D}=0\text{,}0139 \:\mathrm{m^{-1}}$ ; avec cette valeur au numérateur, la seconde approximation donne : $\displaystyle λ_2=\frac{\ln(2\text{,}39)}{D}=0\text{,}0174 \:\mathrm{m^{-1}}$ ; ...de même ensuite : $λ_10=0\text{,}0250 \:\mathrm{m^{-1}}$ ; la suite converge vers $λ=0\text{,}0251 \:\mathrm{m^{-1}}$ . ◊ remarque : cela peut bien sûr être fait automatiquement par une calculatrice.

2.	• D’une façon analogue : $\displaystyle 𝓁_n=∫_0^{t_n} v(t) \: dt=\frac{\ln(1+v_0 \: λ \:t_n )}{λ}$ et donc : $\displaystyle t_n=\frac{1}{λ v_0} \: \left(\mathrm{e}^{n \:λD}-1\right)$ . • L’application numérique donne : $t_2=225 \:\mathrm{s}$ .

• Puisque la force n'est pas constante, il faut calculer le travail infinitésimal sur un petit déplacement élémentaire, puis intégrer sur le déplacement total.
• D’après :

\displaystyle dW=\overset{→}{F}⋅d\overset{⟶}{OM}=-k \:v \:\overset{→}{v}⋅\overset{→}{v} \: dt=-\frac{k \:v_0^{\:3}}{(1+v_0 \: λ \:t)^3} \: dt

on obtient :

$\displaystyle W_n=∫_0^{t_n} -\frac{k \:v_0^{\:3}}{(1+v_0 \: λ \:t)^3} \: dt=\frac{1}{2} m \:v_0^{\:2} \: \left(\frac{1}{(1+v_0 \: λ \:t_n )^2} -1\right)$ .

◊ remarque : on retrouve le théorème de l’énergie cinétique.
• L’application numérique donne :

W_2=-1\text{,}99 \:\mathrm{mJ}

.
◊ remarque :

W_n<0

car le travail du frottement est résistant.

B. EXERCICE D'APPROFONDISSEMENT

Calcul d’une réaction

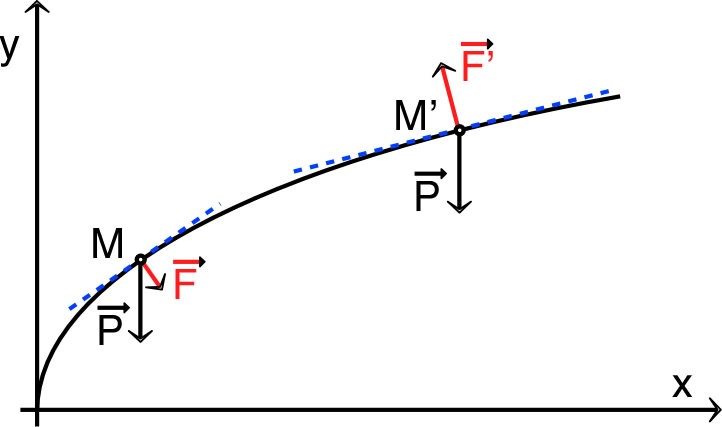
1.	• La courbe est une parabole dont l'axe de symétrie est l'axe horizontal $Ox$ .

2.a.	• Les variations du vecteur position $\overset{⟶}{OM}=x \;\overset{→}{u}_x+y \;\overset{→}{u}_y$ correspondent à $d\overset{⟶}{OM}=dx \;\overset{→}{u}_x+dy \;\overset{→}{u}_y$ et donc le long de la courbe : $\displaystyle \frac{d\overset{⟶}{OM}}{dx}=\overset{→}{u}_x+\frac{dy(x)}{dx} \: \overset{→}{u}_y=\overset{→}{u}_x+\frac{α}{\sqrt{2 \,α \:x}} \: \overset{→}{u}_y=\overset{→}{u}_x+\frac{α}{y} \: \overset{→}{u}_y$ est forcément tangent.

2.b.	• Pour obtenir un vecteur tangent unitaire (vers la droite, donc ascendant), il suffit de diviser le vecteur précédent par sa norme, ce qui peut s'écrire : $\displaystyle \overset{→}{u}_T=\frac{y \;\overset{→}{u}_x+α \;\overset{→}{u}_y}{\sqrt{y^2+α^2}}$ . • Pour obtenir un vecteur unitaire normal (vers le bas), on peut appliquer une rotation de $-\frac{π}{2}$ , ce qui change $\overset{→}{u}_x$ en $-\overset{→}{u}_y$ et $\overset{→}{u}_y$ en $\overset{→}{u}_x$ : $\displaystyle \overset{→}{u}_N=\frac{-y \;\overset{→}{u}_y+α \;\overset{→}{u}_x}{\sqrt{y^2+α^2}}=\frac{α \;\overset{→}{u}_x-y \;\overset{→}{u}_y}{\sqrt{α^2+y^2}}$ .

2.c.	• L'expression générale de la vitesse est : $\displaystyle \overset{→}{v}=\dot{\overset{⟶}{OM}}=\frac{d\overset{⟶}{OM}}{dt}=\left(\overset{→}{u}_x+\frac{α}{y} \, \overset{→}{u}_y \right) \: \dot{x}$ . • Avec $\displaystyle \dot{y}=\frac{α}{y} \, \dot{x}$ l'expression générale de l'accélération est : $\displaystyle \ddot{\overset{⟶}{OM}}=\left(\overset{→}{u}_x+\frac{α}{y} \: \overset{→}{u}_y \right) \: \ddot{x}+\left(-\frac{α}{y^2} \: \dot{y} \; \overset{→}{u}_y \right) \: \dot{x}$ c'est-à-dire : $\displaystyle \overset{→}{a}=\ddot{\overset{⟶}{OM}}=\left(\overset{→}{u}_x+\frac{α}{y} \, \overset{→}{u}_y \right) \: \ddot{x}-\frac{α^2}{y^3} \: \dot{x}^2 \; \overset{→}{u}_y$ .

3.a.	• La relation fondamentale de la dynamique peut s’écrire : $m \:\overset{→}{a}=m \:\overset{→}{g}+\overset{→}{F}$ donc : $\overset{→}{F}=m \:\overset{→}{a}-m \:\overset{→}{g}$ . • La projection sur la normale donne : $\displaystyle \widebar{F}=\left(-m \:\frac{α^2}{y^3} \: \dot{x}^2+m \:g\right) \: \overset{→}{u}_y⋅\overset{→}{u}_N=m .\left(\frac{α^2}{y^3} \: \dot{x}^2-g\right) \, \frac{y}{\sqrt{α^2+y^2}}$ . ◊ remarque : il faut raisonner algébriquement, car on ne connaît pas a priori le sens de $\overset{→}{F}$ .

3.b.	• En l'absence de frottement, la réaction est normale et ne travaille pas ; le théorème de l'énergie mécanique peut s'écrire : $\frac{1}{2} m \:v^2+m \:g \:y=\frac{1}{2} m \:v_0^{\:2}$ donc : $v^2=v_0^{\:2}-2 \,g \:y$ . • D'après ce qui précède : $\displaystyle v^2=\left(1+\frac{α^2}{y^2} \right) \: \dot{x}^2$ et par conséquent : $\displaystyle \dot{x}^2=\frac{v_0^{\:2}-2 \,g \:y}{1+\frac{α^2}{y^2}}$ .

3.c.	• On en déduit par substitution : $\displaystyle \widebar{F}=m .\left(\frac{α^2}{y} \, \frac{v_0^{\:2}-2 \,g \:y^2}{α^2+y^2}-g\right) \, \frac{y}{\sqrt{α^2+y^2}}=m \, \frac{α^2 \: v_0^{\:2}-(3 \,α^2+y^2 ) \: g \:y}{(α^2+y^2 )^{3/2}}$ .

3.d.	• On constate que, peu après le départ ( $y$ petit) : $\displaystyle \widebar{F}≈m \, \frac{v_0^{\:2}-3 \,g \:y}{α}$ ; la réaction est dans le sens de $\overset{→}{u}_N$ , c'est-à-dire vers la droite : pour déplacer le mobile le long du rail, il faut qu'une force s'exerce vers la droite ; or, cela ne peut pas être le poids (vertical). • Au contraire, lorsque le mobile monte “suffisamment”, soit $(3 \,α^2+y^2 ) \: g \:y>α^2 \: v_0^{\:2}$ , la réaction est dans le sens contraire de $\overset{→}{u}_N$ , c'est-à-dire vers la gauche : lorsqu'il monte, le mobile finit par s'arrêter et redescendre, mais si on raisonne sur la projection horizontale du mouvement, il faut pour cela qu'une force s'exerce vers la gauche ; or, cela ne peut pas être le poids (vertical). ◊ remarque : on peut préciser avec les notations simplifiées $\displaystyle y^3+3 \,α^2 \: y>β=\frac{α^2 \: v_0^{\:2}}{g}$ ; on obtient ainsi $\displaystyle y>y_0=η-\frac{1}{η}>0$ avec $\displaystyle η=\frac{α}{2} \, \left(4 \,β+4\:\sqrt{4+β^2}\right)^{1/3}$ . ◊ remarque : la tendance intuitive à s'imaginer que l'action de $\overset{→}{F}$ est principalement de compenser le poids, donc vers le haut, est fausse ; ceci n'est valable que dans des conditions “assez” voisines d'une situation d'équilibre, donc c'est à peu près plausible au voisinage de la position la plus haute du mouvement, mais c'est faux au début.