M. VIII - DYNAMIQUE ; RÉFÉRENTIELS NON GALILÉENS


Notion de force d’inertie

• Soient (O,u→x,u→y,u→z)\left(O\,,\,\overset{→}{u}_x \,,\,\overset{→}{u}_y \,,\,\overset{→}{u}_z\right) un repère d’un référentiel ℛℛ galiléen et (O,u→x′,u→y′,u→z′)\left(O\,,\,\overset{→}{u}{}'_x \,,\,\overset{→}{u}{}'_y \,,\,\overset{→}{u}{}'_z\right) un repère d’un référentiel ℛ′ℛ' non galiléen.

Par dérivation de  OM⟶=OO⟶′+x′u→x′+y′u→y′+z′u→z′\overset{⟶}{OM}=\overset{⟶}{OO}{}'+x' \;\overset{→}{u}{}'_x+y' \;\overset{→}{u}{}'_y+z' \;\overset{→}{u}{}'_z  la vitese d’un point MM par rapport à ℛℛ est liée à celle par rapport à ℛ′ℛ' :
v→=v→′+v→e\overset{→}{v}=\overset{→}{v}{}'+\overset{→}{v}_e
avec  v→e=OO⟶˙′+x′u→˙x′+y′u→˙y′+z′u→˙z′\overset{→}{v}_e=\dot{\overset{⟶}{OO}}{}'+x' \;\dot{\overset{→}{u}}{}'_x+y' \;\dot{\overset{→}{u}}{}'_y+z' \;\dot{\overset{→}{u}}{}'_z   vitesse d’entraînement (vitesse du “point coïncidant” : point fixe de ℛ′ℛ' qui coïncide avec MM à l'instant considéré).

• L’accélération de MM par rapport à ℛℛ est liée à celle par rapport à ℛ′ℛ' :
a→=a→′+a→e+a→c\overset{→}{a}=\overset{→}{a}{}'+\overset{→}{a}_e+\overset{→}{a}_c
avec :
a→e=OO⟶̈′+x′u→̈x′+y′u→̈y′+z′u→̈z′\overset{→}{a}_e=\ddot{\overset{⟶}{OO}}{}'+x' \;\ddot{\overset{→}{u}}{}'_x+y' \;\ddot{\overset{→}{u}}{}'_y+z' \;\ddot{\overset{→}{u}}{}'_z
accélération d’entraînement (accélération du “point coïncidant”) ;
a→c=2(x˙′u→˙x′+y˙′u→˙y′+z˙′u→˙z′)\overset{→}{a}_c=2 \:\left(\dot{x}' \;\dot{\overset{→}{u}}{}'_x+\dot{y}' \;\dot{\overset{→}{u}}{}'_y+\dot{z}' \;\dot{\overset{→}{u}}{}'_z \right)
accélération complémentaire (ou “de Coriolis”).

• Le principe fondamental de la dynamique par rapport à ℛℛ peut donc s’écrire sous la forme :  ∑ℛF→=dp→dt=ma→=ma→′+ma→e+ma→c{\displaystyle∑}_ℛ \overset{→}{F} ={\displaystyle \frac{d\overset{→}{p}}{dt}}=m \;\overset{→}{a}=m \;\overset{→}{a}{}'+m \;\overset{→}{a}_e+m \;\overset{→}{a}_c .

On peut alors écrire par rapport à ℛ′ℛ' :  ∑ℛ′F→=dp→′dt=ma→′{\displaystyle ∑}_{ℛ'} \,\overset{→}{F} ={\displaystyle \frac{d\overset{→}{p}{}'}{dt}}=m \;\overset{→}{a}{}'  à condition d’ajouter des “forces d’inertie” :
∑ℛ′F→=∑ℛF→+f→e+f→c{\displaystyle ∑}_{ℛ'} \,\overset{→}{F} ={\displaystyle ∑}_ℛ \overset{→}{F} +\overset{→}{f}_e+\overset{→}{f}_c  ;
f→e=−ma→e\overset{→}{f}_e=-m \;\overset{→}{a}_e   force d’inertie d’entraînement ;
f→c=−ma→c\overset{→}{f}_c=-m \;\overset{→}{a}_c   force d’inertie complémentaire (ou “de Coriolis”).

◊ remarque : ceci montre le caractère “arbitraire” des “forces” ; elles dépendent du référentiel s’il n’est pas galiléen.

Cas d’une translation

• Pour une translation, les vecteurs de base u→x′\overset{→}{u}{}'_x , u→y′\overset{→}{u}{}'_y et u→z′\overset{→}{u}{}'_z sont constants, par suite :  a→e=OO⟶̈′\overset{→}{a}_e=\ddot{\overset{⟶}{OO}}{}'  et  a→c=0→\overset{→}{a}_c=\overset{→}{0} .

• Ainsi, le passager qui raisonne dans le référentiel ℛ′ℛ' d’une voiture qui ralentit se sent entraîné vers le pare-brise par une force d’inertie  f→e=−ma→e\overset{→}{f}_e=-m \;\overset{→}{a}_e .

Dans le référentiel galiléen ℛℛ lié au sol, c’est le pare-brise qui ralentit et qui est rattrapé par le passager (celui-ci continue d’un mouvement uniforme).

• Pour un passager dans une cabine en “chute libre” dans une champ de pesanteur uniforme, l’accélération de la cabine est :  a→e=g→\overset{→}{a}_e=\overset{→}{g} .

Le passager qui raisonne dans le référentiel ℛ′ℛ' de la cabine a l’impression de subir une force d’inertie d’entraînement  f→e=−ma→e=−mg→\overset{→}{f}_e=-m \;\overset{→}{a}_e=-m \;\overset{→}{g}  compensant son poids :  ma→′=mg→−ma→e=0→m \;\overset{→}{a}{}'=m \;\overset{→}{g}-m \;\overset{→}{a}_e=\overset{→}{0} .  Cette situation est appelée “impesanteur”.

◊ remarque : dans une cabine spatiale en orbite, il n’y a pas rigoureusement impesanteur, d’une part parce qu’il y a toujours plus ou moins de rotation, d’autre part parce que le champ de pesanteur g→\overset{→}{g} n’est pas tout à fait uniforme.

◊ remarque : l’équivalence entre “masse inerte” et “masse pesante” permet de réinterpréter la pesanteur comme une force d’inertie si on définit un système de repérage approprié (théorie de la relativité générale).

📖 exercice n° I.

Cas d’une rotation

• Pour une rotation de vitesse angulaire ω→\overset{→}{ω} :
v→e=OO⟶˙′+x′u→˙x′+y′u→˙y′+z′u→˙z′=OO⟶˙′+ω→×O’M⟶=ω→×OM⟶ \overset{→}{v}_e=\dot{\overset{⟶}{OO}}{}'+x' \;\dot{\overset{→}{u}}{}'_x+y'\;\dot{\overset{→}{u}}{}'_y+z' \;\dot{\overset{→}{u}}{}'_z=\dot{\overset{⟶}{OO}}{}'+\overset{→}{ω} × \overset{⟶}{O\text{’}M}=\overset{→}{ω} × \overset{⟶}{OM}  ;
a→e=ω→˙×OM⟶+ω→×v→e=ω→˙×OM⟶+ω→×(ω→×OM⟶)\overset{→}{a}_e=\dot{\overset{→}{ω}} × \overset{⟶}{OM}+\overset{→}{ω} × \overset{→}{v}_e=\dot{\overset{→}{ω}} × \overset{⟶}{OM}+\overset{→}{ω} × \left(\overset{→}{ω} × \overset{⟶}{OM} \right)  ;
a→c=2ω→×v→′\overset{→}{a}_c=2 \,\overset{→}{ω} × \overset{→}{v}{}' .

Ainsi, pour un point fixe par rapport à ℛ′ℛ' en rotation à vitesse angulaire ω→\overset{→}{ω} constante, on obtient une “force centrifuge” (force d’inertie d’entraînement)  f→e=−ma→e=−mω→×(ω→×OM⟶)=mω2ru→r\overset{→}{f}_e=-m \;\overset{→}{a}_e=-m \;\overset{→}{ω} × \left(\overset{→}{ω} × \overset{⟶}{OM} \right)=m \:ω^2 \: r \;\overset{→}{u}_r  (où rr est la distance entre le point MM et l’axe de rotation).

◊ remarque : par contre, si le point MM n’est pas fixe par rapport à ℛ′ℛ' il faut ajouter la force d’inertie complémentaire :  f→c=−2mω→×v→′\overset{→}{f}_c=-2 \,m \;\overset{→}{ω} × \overset{→}{v}{}' .

• Considérons par exemple un anneau MM mobile sans frottement sur une tige oblique en rotation à la vitesse angulaire ω→\overset{→}{ω} constante.

Par rapport au référentiel ℛ′ℛ' associé à la tige :  ma→′=P→+R→+f→e+f→cm \;\overset{→}{a}{}'=\overset{→}{P}+\overset{→}{R}+\overset{→}{f}_e+\overset{→}{f}_c  avec  f→e=−mω→×(ω→×OM⟶)=mω2x′u→x′\overset{→}{f}_e=-m \;\overset{→}{ω} × \left(\overset{→}{ω} × \overset{⟶}{OM} \right)=m \:ω^2 \: x' \;\overset{→}{u}{}'_x   et   f→c=−2mω→×v→′\overset{→}{f}_c=-2 \:m \;\overset{→}{ω} × \overset{→}{v}{}' .

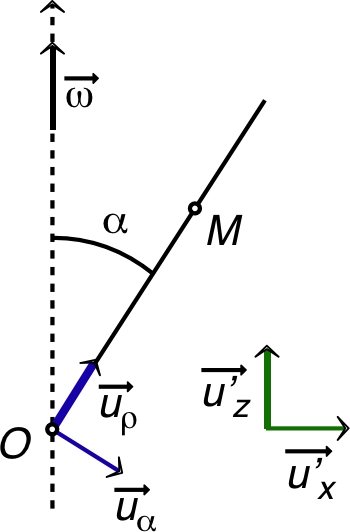
Afin d’exprimer plus simplement les différentes quantités concernées, il est alors pratique d’utiliser dans le plan x′Oz′x'Oz' une base (u→ρ,u→α)\left(\overset{→}{u}_ρ \,,\,\overset{→}{u}_α\right) avec u→ρ\overset{→}{u}_ρ orienté selon OM⟶\overset{⟶}{OM} .

On peut ainsi écrire :  OM⟶=ρu→ρ\overset{⟶}{OM}=ρ \;\overset{→}{u}_ρ  ;
v→′=ρ˙u→ρ\overset{→}{v}{}'=\dot{ρ} \; \overset{→}{u}_ρ  ;  a→′=ρ̈u→ρ\overset{→}{a}{}'=\ddot{ρ}\; \overset{→}{u}_ρ  ;
f→e=mω2ρsin(α)[sin(α)u→ρ+cos(α)u→α]\overset{→}{f}_e=m \:ω^2 \: ρ \; \sin(α) \: \left[\sin(α) \; \overset{→}{u}_ρ+\cos(α) \; \overset{→}{u}_α \right]  ;
f→c=−2mω→×v→′=−2mωρ˙sin(α)u→y′\overset{→}{f}_c=-2 \,m \;\overset{→}{ω} × \overset{→}{v}{}'=-2 \,m \:ω \:\dot{ρ} \; \sin(α) \; \overset{→}{u}{}'_y .
dynNonGal_Im/dynNonGal_Im1.jpg

• En projetant alors la relation de la dynamique sur la direction de u→ρ\overset{→}{u}_ρ on obtient l’équation du mouvement :  ρ̈−ω2sin2(α)ρ=−gcos(α) \ddot{ρ}-ω^2\; \sin^2(α) \: ρ=-g \; \cos(α) .

Une solution particulière de l’équation correspond à l’équilibre relatif (immobilité dans ℛ′ℛ' ) :  ρ̈=0\ddot{ρ}=0   et   ρ=ρe=gcos(α)ω2sin2(α)\displaystyle ρ=ρ_e=\frac{g \;\cos(α)}{ω^2 \; \sin^2(α)} .

En posant  λ=ωsin(α)λ=ω \; \sin(α)  on peut alors écrire la solution générale de l’équation sans second membre sous la forme :  ρ=Aeλt+Be−λtρ=A \:\mathrm{e}^{λ \:t}+B \:\mathrm{e}^{-λ \:t} .

Si on suppose que l’anneau part de la position ρ0ρ_0 avec une vitesse nulle, on obtient finalement la solution :
ρ=ρe+(ρ0−ρe)eλt+e−λt2=ρe+(ρ0−ρe)cosh(λt) \displaystyle ρ=ρ_e+(ρ_0-ρ_e) \, \frac{\mathrm{e}^{λ \:t}+\mathrm{e}^{-λ \:t}}{2}=ρ_e+(ρ_0-ρ_e ) \: \cosh(λ \:t) .

◊ remarque : pour  ρ0<ρeρ_0<ρ_e  l’anneau part vers le bas ; pour  ρ0>ρeρ_0>ρ_e  il part vers le haut ; l’équilibre correspond donc à un équilibre instable.

◊ remarque : ce mouvement de l’anneau provient du fait que la tige tourne par rapport à un référentiel galiléen ; si on laisse la tige fixe dans ℛℛ et qu’on fait seulement tourner un observateur dans ℛ′ℛ' celui-ci voit l’anneau tomber jusqu’en OO (en chute “guidée” par la tige) quelle que soit la position initiale.

• En projetant la relation de la dynamique sur la direction du plan perpendiculaire à u→ρ\overset{→}{u}_ρ on en déduit la force de réaction de la tige :
R→=−mgsin(α)u→α−mω2ρsin(α)cos(α)u→α+2mωρ˙sin(α)u→y′\overset{→}{R}=-m \:g \; \sin(α) \; \overset{→}{u}_α-m \:ω^2 \: ρ \; \sin(α) \: \cos(α) \; \overset{→}{u}_α+2 \,m \:ω \:\dot{ρ} \; \sin(α) \; \overset{→}{u}{}'_y .

◊ remarque : en général, la réaction de la tige n’est pas dans le plan du dessin (à cause du mouvement dans ℛ′ℛ' ).

📖 exercices n° II, III et IV.

Effets de rotation de la Terre

Influence sur le poids

• La force gravitationnelle exercée par la Terre (de masse MTM_T et de centre OO ) sur un point matériel MM (de masse mm ) a pour expression :  F→=−𝒢MTmr2u→r\displaystyle \overset{→}{F}=-𝒢 \: \frac{M_T \: m}{r^2} \: \overset{→}{u}_r  (loi de Newton, analogue à celle de Coulomb pour force électrostatique).

Au voisinage d’un point donné du sol, on peut l’écrire sous la forme  F→=mg→0\overset{→}{F}=m \:\overset{→}{g}_0  avec  g→0=−𝒢MTR2u→r\displaystyle \overset{→}{g}_0=-𝒢 \, \frac{M_T}{R^2} \, \overset{→}{u}_r   (où RR est le rayon terrestre).

• Pour l’étude du mouvement d’un satellite, par rapport à un référentiel galiléen, on peut appeler “poids” cette force de gravitation.

Par contre sur Terre (dans un référentiel terrestre, non-galiléen) le “poids” est par définition  P→=F→+f→e\overset{→}{P}=\overset{→}{F}+\overset{→}{f}_e  incluant la “force centrifuge” f→e\overset{→}{f}_e (force d’inertie d’entraînement de rotation).

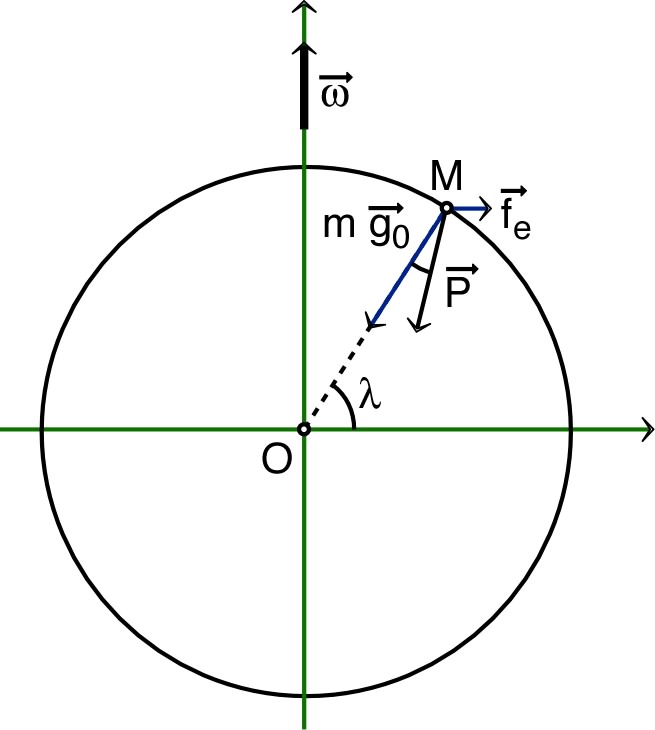
La vitesse angulaire d’un tour par jour  ( ω=7,292.10−5rad.s−1ω=7\text{,}292.{10}^{-5} \; \mathrm{rad.s^{-1}} ) cause une force centrifuge  fe=mω2Rcos(λ) f_e=m\:ω^2 \: R \; \cos(λ)  où λλ est la latitude.

◊ remarque : la rotation correspond à un tour par jour sidéral ( 86164s 86164\:\mathrm{s} ).

• En exprimant  P→=F→+f→e\overset{→}{P}=\overset{→}{F}+\overset{→}{f}_e  sur la base (u→r,u→θ)\left(\overset{→}{u}_r \, ,\,\overset{→}{u}_θ\right) on en déduit une “déviation” αα de la verticale (direction du poids) par rapport à la direction radiale :
tan(α)=ω2Rsin(λ)cos(λ)g0−ω2Rcos2(λ)\displaystyle \tan(α)=\frac{ω^2 \: R \;\sin(λ) \: \cos(λ)}{g_0-ω^2 \: R \;\cos^2(λ)} .
dynNonGal_Im/dynNonGal_Im2.jpg

◊ remarque : à l’équateur, où il est le plus grand, le terme correctif sur PP est :  ω2R=0,034m.s−2ω^2 \: R=0\text{,}034 \;\mathrm{m.s^{-2}}   ce qui n’est pas toujours négligeable ; en outre le calcul exact de P→\overset{→}{P} se complique d’un effet d’aplatissement de la Terre aux pôles.

Déviation de la chute libre vers l’est

• Pour l’étude des mouvements, le terme d’inertie complémentaire intervient aussi ; il provoque par exemple une déviation vers l’est de la chute libre pour un point matériel de vitesse initiale nulle par rapport au référentiel ℛ′ℛ' .

◊ remarque : pour ce calcul on considère  g→≈g→0\overset{→}{g}≈\overset{→}{g}_0  de direction radiale (la correction précédente n'interviendrait qu'au second ordre).

• La relation de la dynamique peut s'écrire par rapport à ℛ′ℛ' :
ma→′=mg→−2mω→×v→′m \;\overset{→}{a}{}'=m \;\overset{→}{g}-2 \,m \;\overset{→}{ω} × \overset{→}{v}{}'  c'est-à-dire :  v→˙′+2ω→×v→′=g→\dot{\overset{→}{v}}{}'+2 \;\overset{→}{ω} × \overset{→}{v}{}'=\overset{→}{g}
(équation analogue à celle avec force magnétique de Lorentz).

Toutefois, la force d’inertie étant faible ( v→′\overset{→}{v}{}' faible), le mouvement vertical est peu modifié et on peut utiliser un “calcul perturbatif” :
r′≈r0′−12gt2r'≈r'_0-\frac{1}{2} g \:t^2  (avec gg quasi uniforme)  ;   r˙′≈−gt\dot{r}{}'≈-g \:t  ;
v→′≈−gtu→r\overset{→}{v}{}'≈-g \:t \;\overset{→}{u}_r  ;  f→c≈2mωgtcos(λ)u→ϕ\overset{→}{f}_c≈2 \,m \:ω \:g \:t \; \cos(λ) \: \overset{→}{u}_ϕ .

Dans un référentiel terrestre cartésien, cela donne :  z″=r′−R=z0″−12gt2z''=r'-R=z''_0-\frac{1}{2} g \:t^2  avec un effet complémentaire :  mẍ″u→x″=f→c≈2mωgtcos(λ)u→ϕm \:\ddot{x}{}'' \; \overset{→}{u}{}''_x=\overset{→}{f}_c≈2 \,m \:ω \:g \:t \; \cos(λ) \; \overset{→}{u}_ϕ .  On en déduit la déviation horizontale (vers l’est) :  x″≈13ωgt3cos(λ)x''≈\frac{1}{3} ω \:g \:t^3 \; \cos(λ) .

◊ remarque : compte tenu de  t≈2z0″g\displaystyle t≈\sqrt{\frac{2 \,z''_0}{g}}  à l’arrivée au sol, on obtient une déviation :  x″≈223ωgz0″3/2cos(λ) \displaystyle x''≈\frac{2 \,\sqrt{2}}{3} \frac{ω}{\sqrt{g}} \:{z''_0}^{3/2} \: \cos(λ)  ;  ainsi pour  z0″≈300m z''_0≈300\:\mathrm{m}  et  λ≈50°λ≈50 \:°  (tour Eiffel) on obtient :  x″≈7,3cmx''≈7\text{,}3 \:\mathrm{cm} .

📖 exercices n° V, VI et VII.

Effets de marée

• Les marées sont surtout associées à la rotation du système Terre-Lune.

On considère le référentiel d'origine GG (centre de la Terre) en translation circulaire (axes de directions fixes) autour de II (centre d'inertie du système). Tous les points y ont la même accélération d'entraînement : la force centrifuge y est partout déterminée par a→G\overset{→}{a}_G .

L’eau du côté proche de la Lune y subit une attraction lunaire de norme supérieure à celle de la “force centrifuge” −ma→G-m\; \overset{→}{a}_G et inversement pour l’eau du côté opposé.

dynNonGal_Im/dynNonGal_Im3.jpg

• La rotation de la Terre sur elle même fait ainsi que l'eau passe deux fois par  jour dans les zones où elle tend à s'écarter du sol. Mais l'effet étant très faible, les marées sont surtout amplifiées par résonance (donc avec déphasage) ; l'effet dépend de la salinité de l'eau et de la grandeur du volume oscillant.

De ce fait, on n'observe pas de marée dans les lacs ; la méditerranée subit des marées plutôt faibles ; l’océan Pacifique résonne plutôt à une marée par jour, alors que l’océan Atlantique résonne plutôt à deux marées par jour.

◊ remarque : l’effet de marée est de plusieurs mètres sur les mers, mais il y a aussi un effet de marée sur la croûte terrestre, de l’ordre de 20cm20 \:\mathrm{cm} .

• Le Soleil exerce aussi une influence sur les marées ; cette influence est toutefois du second ordre, bien que le Soleil soit plus massif, car la distance est plus grande donc la différence des forces est en proportion plus faible.

Les marées sont plus fortes quand la Lune et le Soleil sont alignés avec la Terre (pleine lune et nouvelle lune, périodicité 14,8jours14\text{,}8 \:\mathrm{jours} ).

• Les plans de rotation de la Terre, respectivement autour du Soleil et autour du centre d'inertie Terre-Lune, ne sont pas confondus. Les marées sont donc encore plus fortes quand l'alignement est meilleur (périodicité 173,3jours173\text{,}3 \:\mathrm{jours} ) : il se produit dans la direction d'intersection des plans de rotation (condition dans lesquelles se produisent les éclipses).

dynNonGal_Im/dynNonGal_Im4.jpg
 dynNonGal_Im/dynNonGal_Im5.jpg

Selon les conditions locales, les effets de résonance sont aussi renforcés aux équinoxes (périodicité 182,6jours182\text{,}6 \:\mathrm{jours} ) et aux “équilunes” (périodicité 9,3ans9\text{,}3 \:\mathrm{ans} ) : lorsque le plan de l'équateur est aligné avec l'un ou l'autre des plans de rotation précédents, les effets des deux côtés de la Terre se cumulent mieux car ils sont dans le même alignement (cela favorise la résonance à deux marées par jour).