|
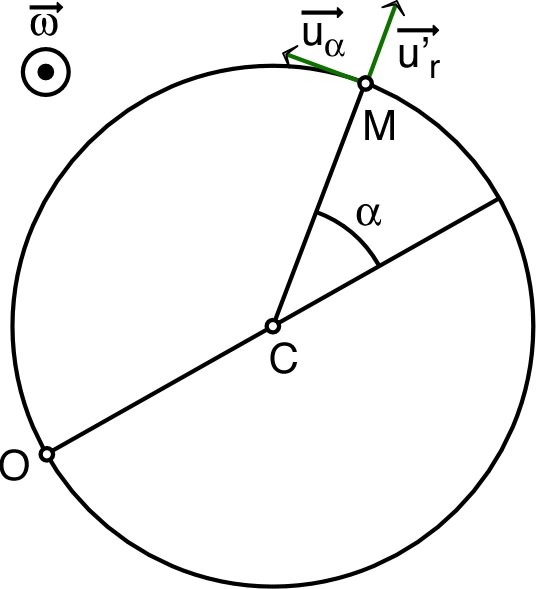
• Par rapport au référentiel tournant
en
coordonnées cylindriques, avec l'origine en bas de la
circonférence, la position de l'anneau vérifie :
c'est-à-dire :
.
◊ remarque : l'expression précédente correspond à la partie
inférieure ; de même
pour la partie supérieure, mais le seul équilibre est
alors pour
et il est évidemment instable.
◊ remarque : on peut aussi repérer par la position angulaire
ou l’abscisse curviligne sur le cercle.
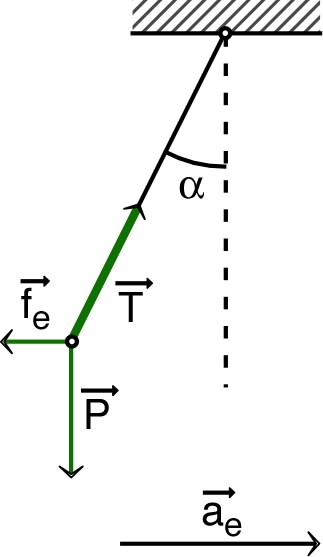
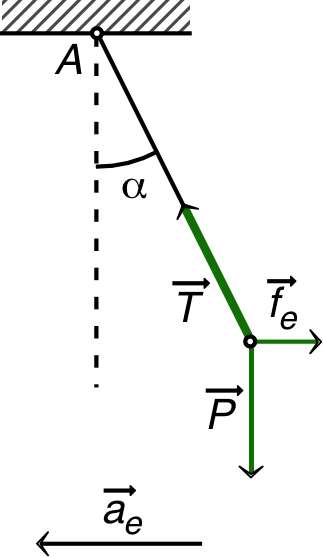
• Puisqu'on cherche une condition d'équilibre, correspondant
à un mouvement relatif nul, on peut considérer la relation
de la dynamique de translation par rapport à
sans
force d'inertie complémentaire. En outre, la force d'inertie
complémentaire
est perpendiculaire au déplacement par rapport à
et
elle ne travaille pas ; elle n’intervient donc généralement
pas dans la méthode d'étude du mouvement par l'énergie
potentielle.
• La réaction de la circonférence ne travaille pas puisqu'il
n'y a pas de frottement ; en particulier elle n'intervient
donc pas dans la méthode de recherche des équilibres par
l'énergie potentielle.
• Pour une rotation de
avec
une vitesse de rotation
constante, la force d'inertie d'entraînement est :
. Or, pour cette force radiale :
avec l'énergie potentielle :
.
• L'énergie potentielle totale de l'anneau par rapport à
peut
donc s’écrire :
.
• Les positions d'équilibre correspondent à la condition
:
d'où on déduit :
ou
(si cette seconde valeur est entre
et
,
c'est-à-dire si
).
◊ remarque : pour la partie supérieure, la condition
d'équilibre est :
d'où on déduit la seule solution :
.
• L'équilibre pour
est stable si :
c'est-à-dire pour :
.
◊ remarque : on retrouve que, s'il n'y a pas équilibre
stable pour
,
l'équilibre stable correspond à l'autre solution :
.
◊ remarque : pour la partie supérieure, on vérifie que la
condition d'équilibre stable est impossible :
.
• Si le coefficient
est
positif (raideur de l'oscillateur), l'énergie potentielle
est
(compte tenu de
) et la période des petites oscillations est :
.
◊ remarque : le calcul de la période suppose que
, ce qui est correct ici pour
à l’ordre d’approximation considéré car :
et
. |