DYNAMIQUE - RÉFÉRENTIELS NON GALILÉENS

DYNAMIQUE - RÉFÉRENTIELS NON GALILÉENS - exercices

Force d’inertie d’entraînement

• Un petit objet, représenté par un point matériel

M

de masse

m

, est posé sur un plateau horizontal ; ce plateau est animé par rapport au sol d’un mouvement d'oscillation verticale sinusoïdale :

z=A \; \cos(ω \,t)

a) Justifier que le référentiel

ℛ'

lié au plateau n'est pas galiléen.
b) En raisonnant par rapport au référentiel

ℛ'

indiquer quelle condition doit satisfaire

ω

pour que le point ne décolle pas du plateau.
c) Application numérique : calculer la fréquence “critique” si

A=5 \:\mathrm{cm}

Moment cinétique par rapport à un référentiel non galiléen

1. • Un pendule simple est constitué par une masse

m

ponctuelle suspendue par un fil de longueur

𝓁

. L’autre extrémité du fil est fixée, en un point

O'

, au plafond d’un train animé d’un mouvement de translation rectiligne horizontal suivant l’axe

Ox

d’un référentiel galiléen

ℛ

. L’accélération

\overset{→}{a}_e

du train par rapport à

ℛ

est constante.
• Déterminer l’angle

α

que fait le fil du pendule avec la direction verticale

O'z'

du référentiel

ℛ'

lorsque le pendule est en “équilibre relatif” pour un observateur placé dans le train.

2. • L’observateur placé dans le train étudie les oscillations du pendule, autour de cette position d’équilibre, dans le plan

x'O'z'

. La position du pendule est repérée par l’angle

θ

du fil par rapport à

O'z'

.
• Calculer le moment cinétique par rapport à

O'

et sa dérivée par rapport au temps par rapport au référentiel

ℛ'

lié au train. En déduire la période des petites oscillations autour de la position d’équilibre.

Mouvement par rapport à un référentiel non galiléen

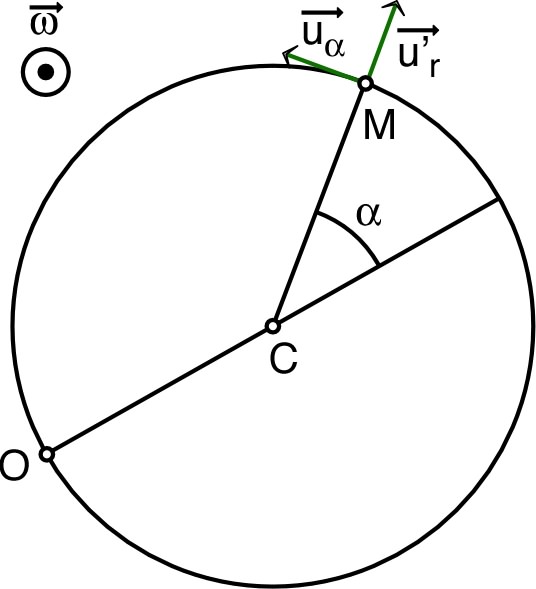
• Une circonférence horizontale de centre

C

et de rayon

R

est animée d’un mouvement de rotation uniforme de vitesse angulaire ω autour d’un axe vertical

Oz

, où

O

est un point de la circonférence.

• Étudier le mouvement d’un point matériel

M

glissant sans frottement sur cette circonférence.

◊ indication : par rapport à un référentiel judicieusement choisi, projeter l’équation du mouvement pour obtenir une équation différentielle sur l’angle

α=\widehat{\left(\overset{⟶}{OC} \,;\overset{⟶}{CM} \right)}

Chute par rapport à un référentiel tournant

• Un manège tourne à la vitesse angulaire constante

ω

autour de son axe

Oz

vertical. On considère des axes

Ox'

Oy'

horizontaux, liés au référentiel

ℛ'

du manège, avec l’origine

O

à une hauteur

h

au dessus du plancher.

1. • On lâche une masse ponctuelle

m

à partir d’un point

A

de l’axe

Ox'

, d’abscisse

x'=b

, avec une vitesse initiale nulle par rapport au référentiel

ℛ'

. Calculer le temps qu’elle met pour atteindre le plancher.

2. • Calculer les coordonnées

x_0

y_0

du point de chute de la masse.

3. • Un fil à plomb, accroché en

A

, est en équilibre par rapport au manège. Le “plomb” se trouve au raz du plancher (sans frotter) ; calculer ses coordonnées

x'_0

y'_0

.

4. • Exprimer les différences

x_0-x'_0

y_0-y'_0

et en donner les développements limités au premier ordre pour

ω

petit.

5. • Écrire les équations différentielles régissant les variations temporelles de

x'

y'

z'

pour le mouvement de chute de la bille (ne pas chercher à les résoudre).

Force d’inertie complémentaire “de Coriolis”

• Un train à grande vitesse (

v=240 \:\mathrm{km.h^{-1}}

) circule dans la direction nord-sud en un lieu de latitude

λ=55 \,° \:\mathrm{nord}

. Préciser la direction et le sens de la force d’inertie complémentaire.
• De quel angle faudrait-il incliner le plan des rails par rapport à l’horizontale si on voulait que la réaction des rails soit rigoureusement perpendiculaire à ce plan ?

Principe et précision de l’expérience d’Eötvös

• La Terre est supposée sphérique et on note

ω

sa vitesse angulaire de rotation sur elle même.
• Deux corps de même poids (c’est-à-dire de même “masse pesante”, ce qui se vérifie précisément avec une balance) sont placés aux extrémités d’un levier de longueur

2 \,𝓁

suspendu en son centre à un fil de quartz très fin, de constante de torsion

C

. On désigne par

m

m'

les “masses inertes” des deux corps (a priori différentes).

1. • Le pendule ainsi constitué, dont la position est repérée par réflexion d’un faisceau lumineux sur un miroir, est placé de telle sorte que le levier soit normal au plan méridien. On fait faire un demi tour à tout l’appareil (y compris le dispositif optique associé au miroir : ce dispositif est fixé sur le même socle que le pendule pour permettre un déplacement aisé). Montrer que la déviation angulaire du levier a pour expression :

\displaystyle Δθ=(m-m')\:\frac{ω^2 \: R\: 𝓁}{C}\: \sin(2 \,λ)

où

R

désigne le rayon terrestre et

λ

la latitude du lieu de l’expérience.

2. • La déviation observée est nulle ; déterminer la précision, caractérisée par le rapport

\displaystyle \frac{m-m'}{m}

, sachant que la période des oscillations du pendule est

\displaystyle T=2π \,\sqrt{\frac{J}{C}}=600 \:\mathrm{s}

(avec un moment d’inertie

J=2 \,m \:𝓁^2

) et que le système optique peut détecter une déviation du faisceau lumineux de

1 \:\mathrm{mm}

à une distance de

2 \:\mathrm{m}

.
• Données :

𝓁=4 \:\mathrm{cm}

;

R=6400 \:\mathrm{km}

;

λ=45 \:°

Oscillation par rapport à un référentiel non galiléen

• Un petit anneau, de masse

m

, peut glisser sans frottement sur une circonférence verticale de rayon

R

, tournant à la vitesse angulaire constante

ω

autour de son diamètre vertical. Discuter, selon la valeur de

ω

, la stabilité de l'anneau au point le plus bas de la circonférence et la période d'oscillation correspondante.

Marées d'équinoxe

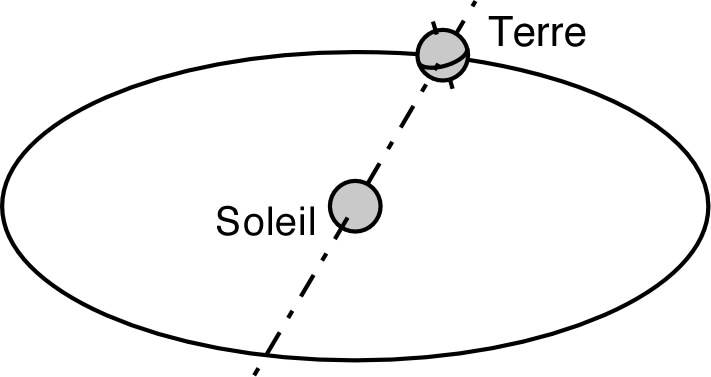
1. a) Les “marées d'équinoxe” dépendent de l'orientation relative de l'axe de rotation de la Terre sur elle même et du plan de son orbite autour du Soleil. Pour un point situé sur l'équateur, représenter l'allure des variations temporelles des “forces de marée” lorsque la Terre est au voisinage du solstice.
b) Représenter de même l'allure de ces variations temporelles lorsque la Terre est au voisinage de l'équinoxe. En déduire l'importance relative des marées d'équinoxe.

2. a) On considère de façon analogue un point situé sur le tropique nord. Représenter l'allure des variations temporelles des “forces de marée” lorsque la Terre est au voisinage de l'équinoxe.
b) Représenter de même l'allure de ces variations temporelles lorsque la Terre est au voisinage du solstice. En déduire l'importance relative des marées d'équinoxe, selon que le lieu considéré est dans une zone de résonance à une marée ou a deux marées par jour.