En posant et et en prenant pour origine la position d’équilibre obtenue pour l’équation du mouvement peut s’écrire :
.
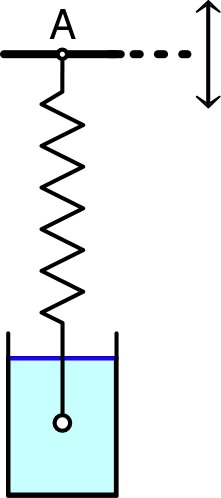
| • On considère un pendule à ressort
vertical avec amortissement visqueux, mis en oscillations
forcées (de pulsation
quelconque) par un mouvement sinusoïdal permanent du support
:
. En posant et et en prenant pour origine la position d’équilibre obtenue pour l’équation du mouvement peut s’écrire : . |
 |
avec .
et .
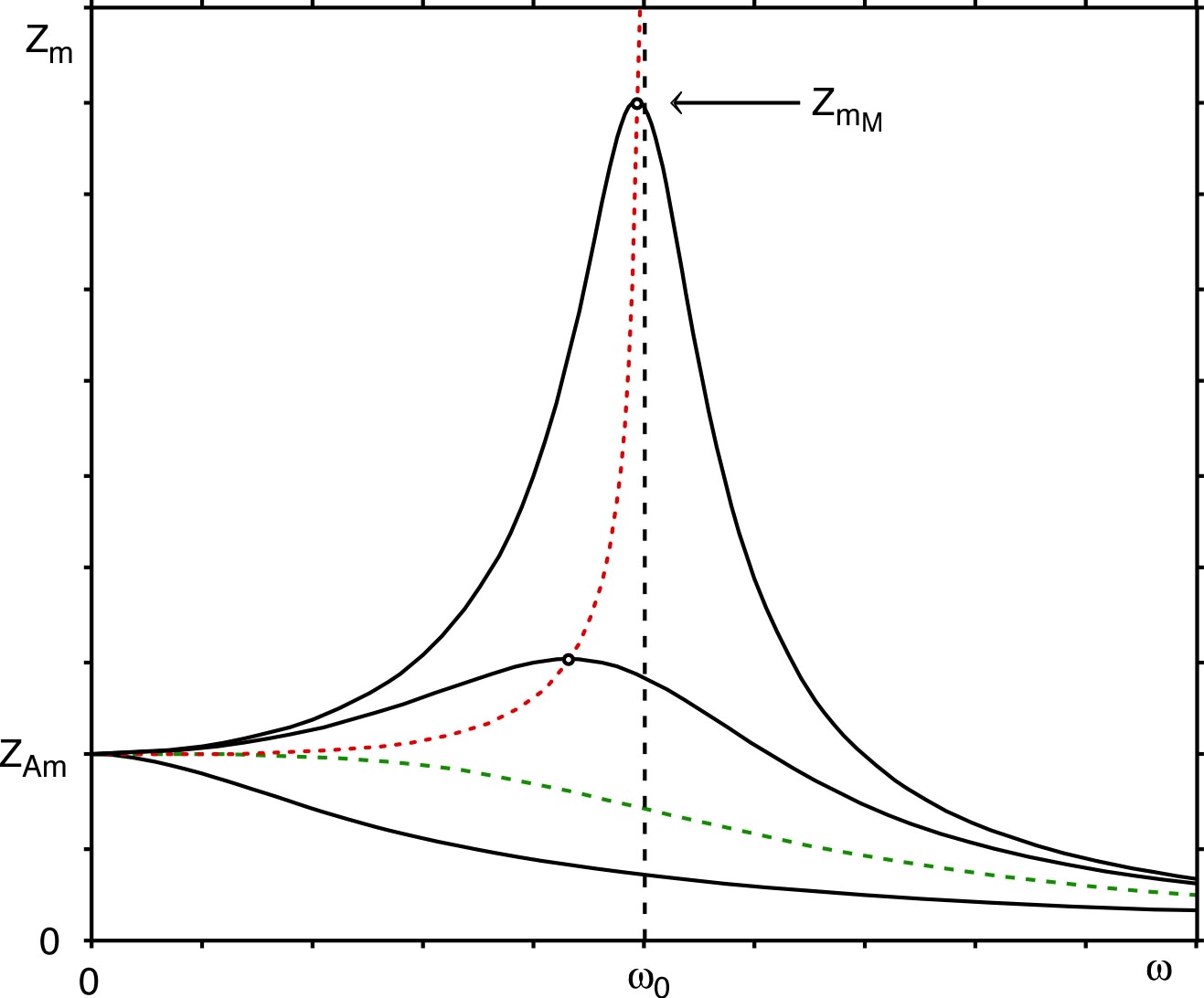
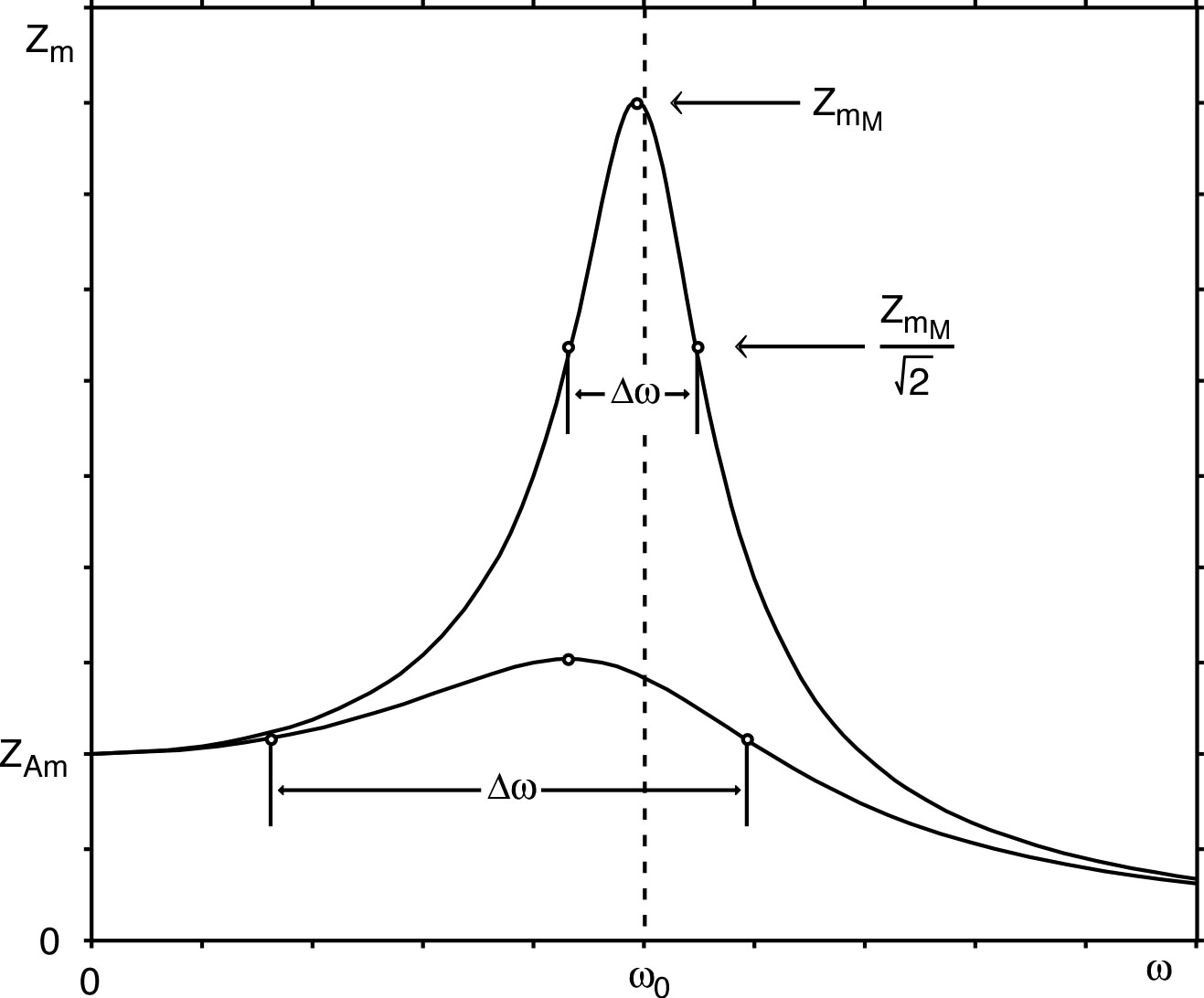
; ;
.
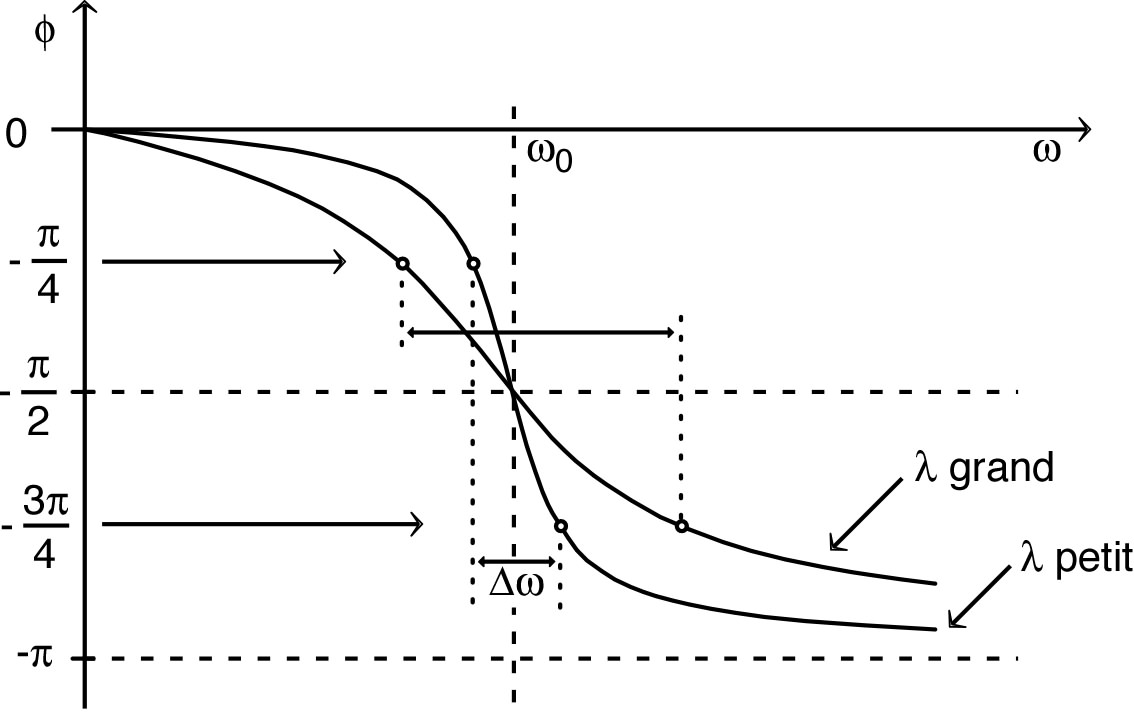
;;
;.
;
;
;
.
