DYNAMIQUE - OSCILLATIONS FORCÉES - corrigé des exercices

A. EXERCICES DE BASE

Amortissement et puissance dissipée

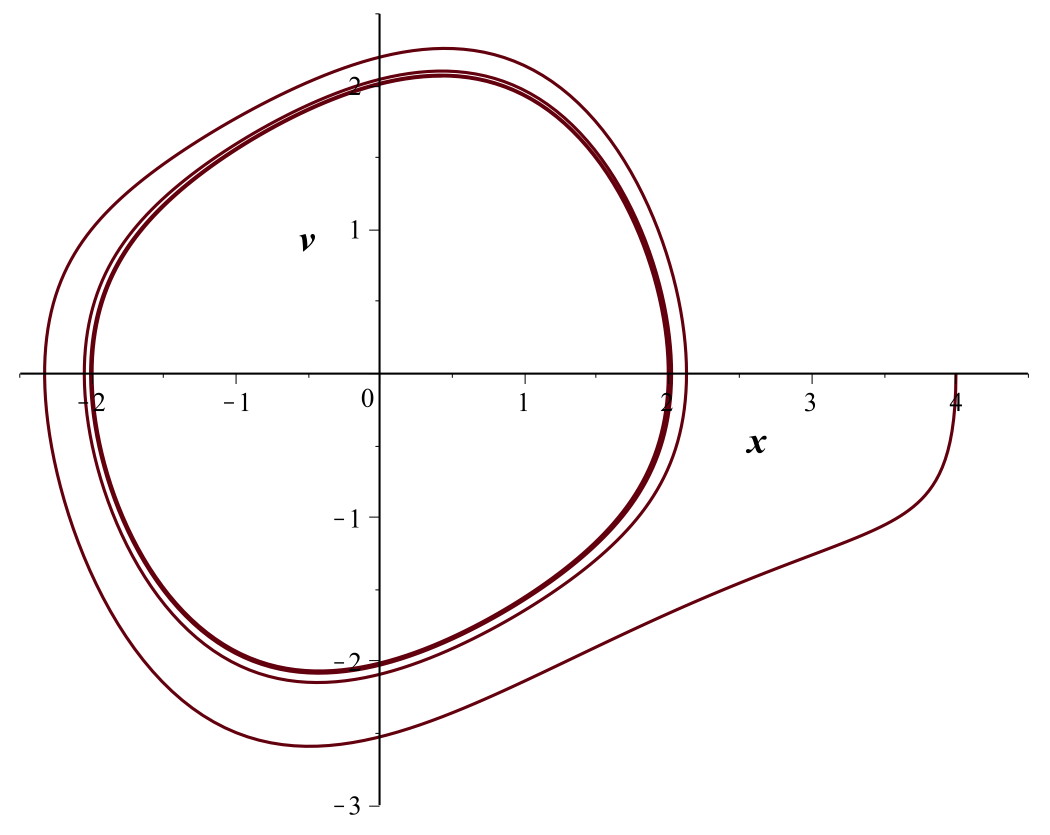
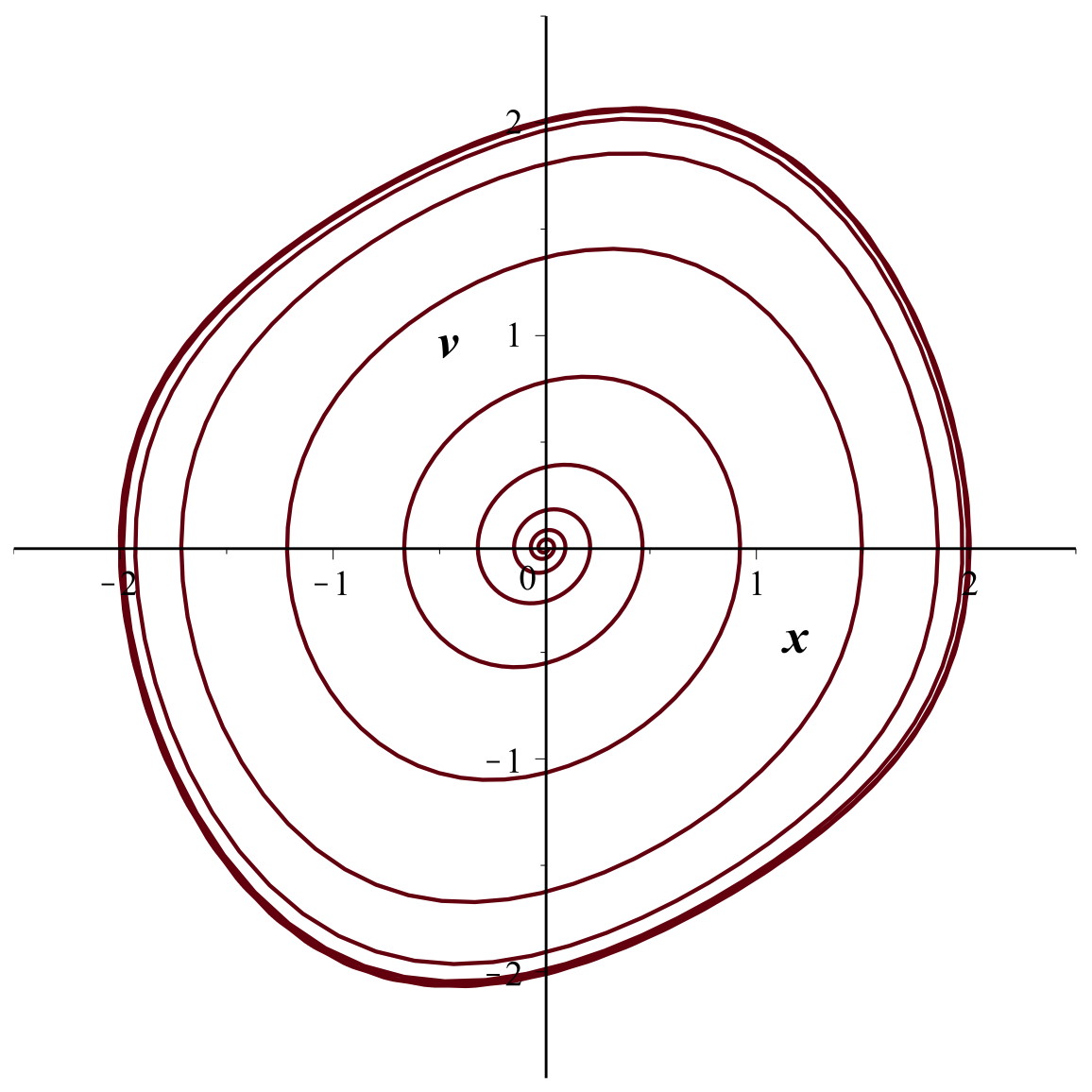
1.	• L’équation de l’oscillateur considéré est de la forme : $\displaystyle \ddot{\underline{x}}+2 \,α \:\dot{\underline{x}}+ω_0^{\:2} \: \underline{x}=\frac{F_0}{m} \: \mathrm{e}^{\mathrm{j}ωt}$ (en notations complexes) où $m$ est le coefficient d’inertie de l’oscillateur, où $k=m \:ω_0^{\:2}$ est son coefficient de “raideur” et où $f=2 \,α \:m$ correspond au “frottement” équivalent causant l’amortissement. • La solution est : $\underline{x}=X_m \; \mathrm{e}^{\mathrm{j}(ωt+ϕ)}$ avec $\displaystyle X_m=\frac{F_0}{m \:\sqrt{\left(ω^2-ω_0^{\:2} \right)^2+(2 \,α \:ω)^2}}$ et $\displaystyle ϕ=\arctan\left(\frac{2 \,α \:ω}{ω^2-ω_0^{\:2}}\right)$ ; la vitesse est donc : $\underline{v}=\dot{\underline{x}}=\mathrm{j} \:ω \:X_m \; \mathrm{e}^{\mathrm{j}(ωt+ϕ) }$ . • La puissance étant une quantité “quadratique”, il est plus simple d’utiliser les notations réelles : $x(t)=X_m \; \cos(ω \,t+ϕ)$ et $v(t)=-ω \:X_m \; \sin(ω \,t+ϕ)$ . On obtient ainsi : $p(ω,t)=\overset{→}{F}∙\overset{→}{v}=F .v=-ω \:X_m \: F_0 \; \cos(ω \,t+ϕ) \; \sin(ω \,t+ϕ)$ $=-\frac{1}{2} ω \:X_m \: F_0 .\left[\sin(2ω \,t+ϕ)+\sin(ϕ) \right]$ ; $P(ω)=〈 p(ω,t) 〉=-\frac{1}{2} ω \:X_m \: F_0 \; \sin(ϕ)$ avec $\displaystyle \sin(ϕ)=-\frac{2 \,α \:ω}{\sqrt{\left(ω^2-ω_0^{\:2} \right)^2+(2 \,α \:ω)^2}}$ ; $\displaystyle P(ω)=\frac{α \:ω^2 \: F_0^{\:2}}{m ∙ \left[\left(ω^2-ω_0^{\:2} \right)^2+(2 \,α \:ω)^2 \right] }$ .

2.	• L'étude peut être simplifiée en utilisant les notations réduites $\displaystyle \frac{α}{ω_0}$ et $\displaystyle \frac{ω}{ω_0}$ ainsi que $\displaystyle P_0=\frac{F_0^{\:2}}{m \:ω_0}$ : $\displaystyle \frac{P}{P_0} =\frac{\frac{α}{ω_0}\: \left(\frac{ω}{ω_0} \right)^2}{\left(\left(\frac{ω}{ω_0} \right)^2-1\right)^2+\left(2 \frac{α}{ω_0} \frac{ω}{ω_0} \right)^2}$ . • Avec ces notations, la courbe de résonance en puissance a l'allure suivante :

Diagramme de phase

• La solution des équations du mouvement peut s’écrire :

$x=X_m \; \cos(ω \,t+ϕ)$ ; $\displaystyle \frac{\dot{x}}{ω_0} =-\frac{ω}{ω_0} \, X_m \; \sin(ω \,t+ϕ)$ .

• Le diagramme de phase correspond donc à une ellipse de demi-axe horizontal

X_m

et de demi-axe vertical

\displaystyle \frac{ω}{ω_0} \, X_m

(l’ellipse est aplatie horizontalement ou verticalement selon que

ω

est inférieur ou supérieur à

ω_0

B. EXERCICE D'APPROFONDISSEMENT

Oscillations d'un pont suspendu

1.	◊ remarque : pour simplifier les notations, on peut utiliser $L$ comme unité de longueur et $\displaystyle \frac{1}{ω_0}$ comme unité de temps. • Avec $\displaystyle \frac{α}{ω_0} =0\text{,}25$ l'intégration numérique montre des oscillations (modérément) amorties, mais au lieu de tendre vers zéro (comme pour l'oscillateur linéaire) le mouvement tend vers un cycle limite avec des extremums pour $\displaystyle \frac{x}{L}=±2$ . L'interaction avec le vent apporte l'énergie nécessaire pour entretenir les oscillations en compensant en moyenne les pertes par frottement.

2.	• Avec ici encore $\displaystyle \frac{α}{ω_0} =0\text{,}25$ (pour mieux comparer) l'intégration numérique montre des oscillations progressivement amplifiées ; le mouvement tend vers le même cycle limite. L'interaction avec le vent apporte en moyenne suffisamment d'énergie pour forcer les oscillations. • Il est intéressant de remarquer que la position $x_0=0$ (avec une vitesse nulle) correspond à un équilibre ; ce dernier est toutefois instable et il suffit d'un écart initial très faible pour aboutir à des oscillations forcées (d'où les conditions initiales proposées par l'énoncé). • On constate par ailleurs que l'approche du cycle limite nécessite nettement plus de pseudo-périodes dans le cas amplifié (ici sept fois plus). Dans ce cas l'action du vent ne se limite plus à limiter les pertes d'énergie dues aux frottements, mais doit apporter l'énergie nécessaire à l'oscillation en plus de compenser les pertes.