OSCILLATIONS MÉCANIQUES FORCÉES

OSCILLATIONS MÉCANIQUES FORCÉES - corrigé du TP

Oscillations en translation

Effet du ressort

• Afin d'estimer l'effet éventuel de la masse

m_r

du (des) ressorts sur la masse de “l'oscillateur” (si cette masse n'est pas négligeable), on peut commencer par envisager le cas d'un pendule à ressort simple en oscillations libres.

• Pour un ressort de longueur

L

, on peut noter par une coordonnée

𝓁∈[0\:; L]

la position d'un élément de ressort infinitésimal de longueur

d𝓁

. Si la vitesse du point de fixation

A

est nulle et que la vitesse du mobile

M

est

v

, alors la portion

d𝓁

du ressort a une vitesse

\displaystyle v_𝓁=\frac{𝓁}{L}\, v

.

◊ remarque : ceci suppose que le ressort a tout de même une masse assez faible et une raideur assez grande pour pouvoir négliger le délai de propagation de l'énergie depuis

A

jusqu'à

M

.

• La masse de l'élément infinitésimal étant

\displaystyle dm_r=\frac{d𝓁}{L} \, m_r

, l'énergie cinétique emmagasinée par le ressort est :

\displaystyle E_{cr}=∫_0^L \frac{1}{2} v_𝓁^{\:2} \: dm_r =\frac{1}{2} m_r \: v^2 \: \frac{1}{L^3} \: ∫_0^L 𝓁^2 \: d𝓁=\frac{1}{2} \frac{m_r}{3} v^2

. On aboutit donc à la conclusion que tout se passe comme si la masse du système mobile était augmentée de

\displaystyle \frac{m_r}{3}

(au moins en première approximation, suffisante pour un terme décrivant une faible correction).

• Dans le cas d'un pendule en oscillations forcées, le mouvement du point de suspension

A

rend l'interprétation moins directe. En raisonnant de même vis à vis du mouvement relatif de

M

par rapport au référentiel de

A

(non galiléen), on obtient la même équation du mouvement avec l'action motrice causée sur

M

par la force d'inertie d'entraînement. Le résultat est donc le même.

◊ remarque : l'interprétation est par contre moins simple si on ne peut pas négliger le délai de propagation de l'énergie depuis

A

jusqu'à

M

; or l'expérience montre que c'est peut être parfois le cas puisqu'on observe à certaines fréquences des résonances d'ondes stationnaires du ressort (probablement non indépendantes des vibrations parasites du support) perturbant la résonance “principale” de l'oscillateur ; une modélisation plus complète nécessiterait d'envisager des “oscillateurs couplés”.

Effet du fluide

Contribution à l'inertie de l'oscillateur

• Lorsqu'on réalise un frottement fluide en faisant déplacer un mobile dans un fluide, le problème revient à étudier un système constitué d'un point matériel en interaction avec le fluide, décrit par la mécanique... des fluides. Est-il alors possible de ramener la description à une forme analogue à celle de la mécanique du point matériel ? On peut pour cela raisonner de façon un peu analogue à celle utilisée précédemment pour “incorporer” certaines propriétés du ressort dans les propriétés du point matériel représentatif.

• En plus de la poussée d'Archimède “statique” (et à part les forces de capillarité et de portance) le solide en mouvement est soumis à des forces de poussée “dynamique” et de frottement (visqueux ou turbulent).

La mise en mouvement du solide nécessite la mise en mouvement d'une masse de fluide

m_e

environ équivalente à celle du fluide “déplacé”, mais l'énergie correspondante peut en pratique se répartir sur une quantité de fluide plus grande (qui se déplace alors d'autant moins vite).

• Pour préciser cet effet, on peut comparer au cas de l'énergie potentielle de pesanteur transmise au fluide (et de ce fait intervenant dans la poussée d'Archimède) : si le double de fluide se déplace deux fois moins, cela correspond à la même variation d'énergie potentielle ; la poussée d'Archimède ne dépend donc pas du détail de la circulation du fluide.

Au contraire pour l'énergie cinétique, si le double de fluide se déplace deux fois moins (donc deux fois moins vite), l'énergie cinétique qui lui est transmise est deux fois plus faible. C'est donc équivalent à une masse moitié de fluide mise en mouvement autant que le mobile. Le calcul théorique (en mécanique des fluides) pour une sphère dans un fluide parfait en régime laminaire donne

m_e=\frac{1}{2} m_d

.

• Dans le cas étudié ici, le caractère turbulent du frottement semble non négligeable pour les plus grands frottements. En utilisant un modèle empirique avec

m_e=β \:m_d

, l'expérience montre que

β≈0\text{,}75

en moyenne (variant de

≈0\text{,}5

≈1\text{,}0

selon la forme du mobile et sa taille relative par rapport au tube ; toute précision supplémentaire nécessiterait une étude en mécanique des fluides).

Caractère laminaire ou turbulent du frottement

• En régime laminaire, une étude des forces de viscosité sur un cylindre de rayon

r

en mouvement dans un tube de rayon

r_{max}

aboutit à un coefficient de frottement visqueux de la forme

\displaystyle λ=\frac{λ_0}{\ln\left(\frac{r}{r_{max}}\right)+\frac{r_{max}^{\:2}-r^2}{r_{max}^{\:2}+r^2}}

.

La comparaison de l'amortissement des courbes de résonance expérimentales et du rayon de la plaquette utilisée pour réaliser le frottement semble toutefois peu compatible avec un tel comportement. Ceci suggère que le frottement n'est pas vraiment laminaire.

• L'étude du nombre de Reynolds permet de tester le type de comportement du fluide :

les dimensions caractéristiques (mobile et eau circulant autour) sont de l'ordre de $D≈1\text{,}5 \:\mathrm{cm}$ ;
les vitesses maximales correspondent à un déplacement $Z_m≈10 \:\mathrm{cm}$ en une durée $\displaystyle \frac{T}{4}≈0\text{,}15 \:\mathrm{s}$ ; c'est-à-dire $v≈0\text{,}6 \:\mathrm{m .s^{-1}}$ ;
la masse volumique de l'eau est $ρ≈{10}^3 \: \mathrm{kg .m^{-3}}$ et sa viscosité est $η≈{10}^{-3} \: \mathrm{Pa .s}$ ;
le nombre de Reynolds est donc : $\displaystyle Re≈\frac{ρ \,D \,v}{η}≈{10}^4>2000$ .

• Pour des valeurs aussi grandes, le caractère turbulent du fluide peut être prépondérant. Ceci ne remet pas en cause complètement l'allure des courbes : seule la partie haute des pics de résonance aigus est probablement modifiée de façon non négligeable (c'est là que sont atteintes les vitesses maximales).

La résolution exacte de l'équation différentielle du mouvement n'étant pas possible pour un frottement proportionnel à

v^2

, une méthode peut consister à intégrer numériquement avec un logiciel de calcul formel. Une autre méthode peut être d'ajuster avec un tableur les coefficients d'un développement trigonométrique en série d'harmoniques. On constate ainsi que la forme des courbes de résonance est peu modifiée mais que, pour un même maximum, le frottement turbulent semble donner un pic légèrement plus arrondi au sommet. En outre, pour les forts amortissements, le frottement turbulent diminue un peu plus la fréquence de résonance au dessous de la fréquence propre.

◊ remarque : pour de telles simulations numériques, on peut simplifier l'équation en raisonnant avec des variables réduites

\displaystyle ζ=\frac{z}{Z_{Am}}

\displaystyle u=\frac{ω}{ω_0}

τ=ω_0 \: t

; dans le cas du frottement laminaire, ceci revient à considérer l'équation réduite :

\displaystyle \frac{d^2ζ}{{dτ}^2}+2 \:α′ \, \frac{dζ}{dτ}+ζ=\cos(u \:τ)

avec

\displaystyle α′=\frac{α}{ω_0}

; le cas du frottement turbulent est un peu différent puisqu'on obtient :

\displaystyle \frac{d^2ζ}{{dτ}^2}+2 \,α′_2 .\left(\frac{dζ}{dτ}\right)^2+ζ=\cos(u \:τ)

avec

α′_2=α_2 \: Z_{Am}

.

◊ remarque : le commentaire précédent permet au passage de prendre conscience que, pour un frottement turbulent, augmenter l'amplitude de l'oscillation a un effet équivalent à une augmentation du coefficient de frottement ; ceci n'est pas indépendant de la partie suivante.

• En pratique, la méthode utilisée ici est assez longue : pour chaque fréquence on intègre numériquement et on observe l'amplitude atteinte après amortissement du régime transitoire.

On peut ainsi obtenir point par point la courbe de résonance, pour comparer au frottement laminaire. Avec un frottement faible, la courbe n'est pratiquement pas changée.

Pour des frottements plus importants, on constate une petite diminution de la fréquence de résonance (mais les incertitudes ne sont pas négligeables).

◊ remarque : pour tester cette méthode d'intégration numérique, on peut l'appliquer pour un frottement laminaire et vérifier qu'on retrouve bien le résultat obtenu par intégration formelle.

• Puisque les oscillations forcées sont quasi-sinusoïdales, une autre méthode peut consister à utiliser une approximation par série de Fourier, en supposant qu'un très petit nombre de termes suffit. Les résultats obtenus sont les mêmes.

Problème des forts frottements

• Pour les frottements importants, on observe un autre problème expérimental qui semble associé à une oscillation transversale parasite. La grande plaquette utilisée pour réaliser le frottement passe près des bords du tube : lorsque le déplacement est relativement rapide, la moindre dissymétrie fait que la plaquette semble attirée sur le côté par une sorte d'effet Venturi, ce qui semble augmenter le frottement (turbulences importantes). Ce phénomène est alors hélas trop prépondérant pour qu'on puisse l'éviter (par exemple en cherchant à améliorer le guidage de la tige de l'oscillateur) : toute tentative est sans effet ou perturbe plus l'oscillateur qu'elle ne résout le problème.

Ce problème semble moins affecter les mesures effectuées avec une faible amplitude du moteur, mais celles-ci sont de ce fait peu précises.

Conditions de décrochage

• Au niveau du point de fixation

A

en haut du ressort, la condition d'équilibre en l'absence d'oscillations peut s'écrire :

k .\left((z_{A0}-z_0 )-𝓁_0 \right)=m \:g

(en considérant

m

g

renormalisés tenant compte de l'interaction avec l'eau).

La condition pour que le ressort reste tendu lors des oscillations peut s'écrire :

k .\left((z_A-z)-𝓁_0 \right)>0

avec les variations :

z_A=z_{A0}+Z_{Am}\; \cos(ω \:t)

z=z_0+Z_m\; \cos(ω \:t+ϕ)

. Ceci peut s'écrire sous la forme :

$\displaystyle \frac{m \:g}{k}+\left(Z_{Am}-Z_m \; \cos(ϕ) \right) \; \cos(ω \:t)+Z_m \; \sin(ϕ) \; \sin(ω \:t)>0$ ;
$\displaystyle \frac{m \:g}{k}+\sqrt{\left(Z_{Am}-Z_m \; \cos(ϕ) \right)^2+\left(Z_m \; \sin(ϕ) \,\right)^2} \:\; \cos(ω \:t+ψ)>0$ .

Pour que cela soit vérifié à tout instant, il faut imposer :

\displaystyle \frac{m \:g}{k}>\sqrt{\left(Z_{Am}-Z_m \; \cos(ϕ) \right)^2+\left(Z_m \; \sin(ϕ) \right)^2}

.

En outre, les oscillations forcées correspondent à :

$k=m \:ω_0^{\:2}$ ; $\displaystyle Z_m=Z_{Am} \, \frac{ω_0^{\:2}}{\sqrt{\left(ω_0^{\:2}-ω^2 \right)^2+(2 \,α \:ω)^2}}$ ;
$\displaystyle \cos(ϕ)=\frac{ω_0^{\:2}-ω^2}{\sqrt{\left(ω_0^{\:2}-ω^2 \right)^2+(2 \,α \:ω)^2}}$ ; $\displaystyle \sin(ϕ)=\frac{-2 \,α \:ω}{\sqrt{\left(ω_0^{\:2}-ω^2 \right)^2+(2 \,α \:ω)^2}}$ .

Ceci donne :

\displaystyle \frac{g}{Z_m} >\sqrt{\frac{\left((2 \,α \:ω)^2-ω^2.\left(ω_0^{\:2}-ω^2 \right)^2 \right)^2+ω_0^{\:4}.(2 \,α \:ω)^2}{\left(ω_0^{\:2}-ω^2 \right)^2+(2 \,α \:ω)^2}}

.

• Les situations où risque le plus de se produire le décrochage sont celles où l'amplitude est la plus grande, c'est-à-dire au voisinage de la résonance (

ω≈ω_0

) et à faible amortissement (

α≪ω_0

) ; on peut alors remarquer que :

\displaystyle \sqrt{\frac{\left((2 \,α \:ω)^2-ω^2.\left(ω_0^{\:2}-ω^2 \right)^2 \right)^2+ω_0^{\:4}.(2 \,α \:ω)^2}{\left(ω_0^{\:2}-ω^2 \right)^2+(2 \,α \:ω)^2}}≈ω_0^{\:2} .\left(1+2 \,\frac{ω-ω_0}{ω_0} \right)≈ω^2

.

La condition limite peut alors être remplacée par celle, nettement plus simple, obtenue pour un point matériel simplement posé sur un plateau horizontal oscillant avec la même amplitude :

\displaystyle Z_m<\frac{g}{ω^2}

.

• Pour éviter le décrochage, il suffit de diminuer l'amplitude du mouvement du moteur au niveau de la roue excentrée (puis éventuellement de multiplier les mesures par le coefficient de réduction lors des comparaisons des différentes expériences). Hélas, la roue motrice ne dispose pas de position de fixation à

0\text{,}5 \:\mathrm{cm}

de l'axe (bien que proche de l'axe, cela semble réalisable, mais nous ne disposons pas au lycée d'un outillage assez précis ; en outre, cela serait impossible à moins de

0\text{,}5 \:\mathrm{cm}

Pour compenser, nous avons bricolé des réducteurs d'amplitude qu'on peut aisément placer au niveau de la poulie (simples bras de levier qui divisent l'amplitude par deux ou trois). Il est nécessaire (et suffisant) de faire un tour de fil autour de chacune des deux vis pour éviter le glissement. Les résultats ainsi obtenus sont tout à fait concluants.

Les rapports de réduction sont :

$0\text{,}326±0\text{,}014$ ; $0\text{,}380±0\text{,}015$ ; $0\text{,}508±0\text{,}023$ ; $0\text{,}531±0\text{,}024$ ; $0\text{,}556±0\text{,}025$ .

◊ remarque : de nouveaux modèles de ces montages ont par la suite été commercialisés ; les répartitions des masses y ont été modifiées pour éviter le décrochage ; le paradoxe est que, si cela est certainement mieux pour les élèves de l'enseignement secondaire, c'est au contraire plutôt moins bien pour l'enseignement supérieur dans la mesure où nos étudiants sont ainsi forcés à réfléchir de façon moins superficielle, ce qui est excellent pour la formation des ingénieurs.

Résultats expérimentaux

Étalonnage des ressorts

• Les raideurs de ressorts ont été étalonnées par élongation ; les étudiants n'ont pas déterminé les incertitudes mais on peut les estimer d'après la dispersion des mesures :

k=19\text{,}68±0\text{,}30 \:\mathrm{N.m^{-1}}

◊ remarque : les différents montages ont des ressorts du même modèle, mais qui pourraient avoir des raideurs légèrement différentes ; les écarts observés dans les mesures des étudiants ne sont pas dus à cela car ils sont semblables quand on compare plusieurs mesures obtenues pour un même ressort (il s'agit de maladresses de manipulation).

Fréquence d'oscillation affichée

• Les moteurs forçant les oscillations sont munis d'un affichage de la fréquence ; un contrôle d'étalonnage (en chronométrant quelques dizaines de périodes) montre qu'ils donnent des indications correctes pour la précision requise ici (

≈±1 \:%

◊ remarque : les étudiants n'ont pas déterminé les incertitudes ; deux points semblant aberrants ont été exclus de l'ajustement.

Observation du décrochage

• Avant d'aborder les courbes de résonance obtenues, il est intéressant d'observer l'effet du décrochage sur l'une d'entre elles, obtenue par un groupe n'ayant pas pris les précautions nécessaires : exemple avec une “petite” masse (un seul bloc d'acier) et un frottement “moyen” (plaquette de taille intermédiaire).

On observe effectivement que tous les points dépassant la limite de décrochage sont systématiquement biaisés.

Courbes de résonance

• Des séries de mesure ont été demandées pour chaque masse disponible (un, deux ou trois blocs d'acier).

Pour chaque masse, une comparaison des trois frottements disponibles était demandée (la plaquette imposant le frottement dans l'eau pouvant être petite, moyenne ou grande) ; cela n'a été réalisé que pour deux ou trois blocs d'acier.

• Avec deux blocs d'acier, la masse oscillante comporte deux blocs, la tige de fixation, la plaquette et les contributions du ressort et de l'eau, soit respectivement :

m′=137\text{,}5\:\mathrm{g}

;

144\text{,}4\:\mathrm{g}

;

143\text{,}4\:\mathrm{g}

Avec faible frottement, les limites de décrochage, pour les différents réglages possibles, montrent clairement la nécessité d'utiliser un réducteur (celui avec seulement un facteur ≈ 2 est même insuffisant). Par contre, pour obtenir plus de précision, la réduction d'amplitude n'est utilisée que pour les mesures qui le nécessitent.

Les mesures sont bien modélisées par l'expression théorique pour un frottement laminaire, ce qui est plausible pour un frottement faible.

Pour les frottements plus grands, les limites de décrochage ne sont pas atteintes (en utilisant toutefois le réglage “standard” approprié).

Les mesures sont bien modélisées par l'expression théorique pour un frottement laminaire, ce qui est relativement inattendu pour le frottement le plus fort ; les incertitudes de mesure sont toutefois assez grandes.

• Avec trois blocs d'acier, la masse oscillante comporte deux blocs, la tige de fixation, la plaquette et les contributions du ressort et de l'eau, soit respectivement :

m′=190\text{,}2\:\mathrm{g}

;

192\text{,}3\:\mathrm{g}

;

206\text{,}3\:\mathrm{g}

Avec un faible frottement, les limites de décrochage, pour les différents réglages possibles, montrent clairement la nécessité d'utiliser un réducteur.

Les mesures sont bien modélisées par l'expression théorique pour un frottement laminaire, ce qui est plausible pour un frottement faible.

Pour le frottement moyen, la limite de décrochage avec réglage “standard” n'est pas atteinte mais très proche ; un réducteur est préférable.

Ici encore, les mesures sont bien modélisées par l'expression théorique pour un frottement laminaire.

Pour le frottement le plus grand, un réglage “standard” approprié est suffisant.

Les mesures sont moins bien modélisées par l'expression théorique pour un frottement laminaire : on observe une fréquence de résonance un peu diminuée comme prévu théoriquement pour un effet turbulent. Ceci qui n'est pas étonnant pour le frottement le plus fort, mais on doit se demander pourquoi cela n'est pas observé avec seulement deux blocs d'acier. Une observation attentive montre qu'avec trois blocs d'acier (ensemble plus long) la circulation de l'eau du tube sur les côtés du mobile est plus perturbée et il se produit des oscillations transversales parasites. De ce fait, les turbulences sont plus importantes et deviennent suffisantes pour influencer le comportement.

Frottement fluide

• La détermination expérimentale des coefficients de frottement, ajustés pour modéliser au mieux les courbes de résonance, pourrait en principe permettre une étude en fonction de la taille des plaquettes utilisées pour cela. La circulation de l'eau entre le dispositif et la paroi du tube est toutefois complexe et fait intervenir la mécanique des fluides de façon trop délicate. Aucune interprétation convaincante n'a pu être proposée.

Oscillations en rotation

Dispositif expérimental

◊ remarque : cette partie est associée au chapitre suivant, décrivant les systèmes en rotation ; elle est placée ici pour des raisons d'organisation des séances de TP.

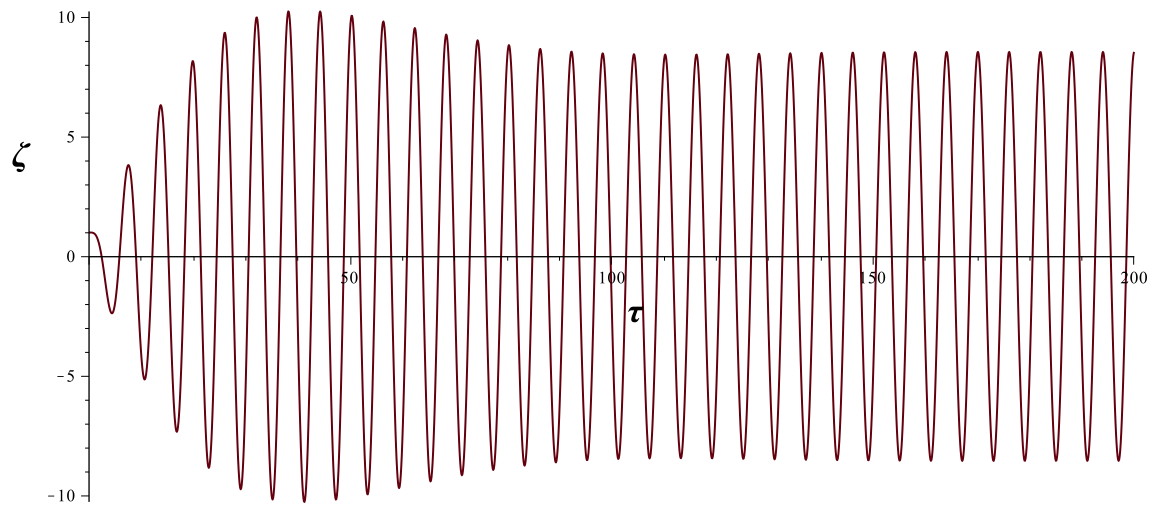
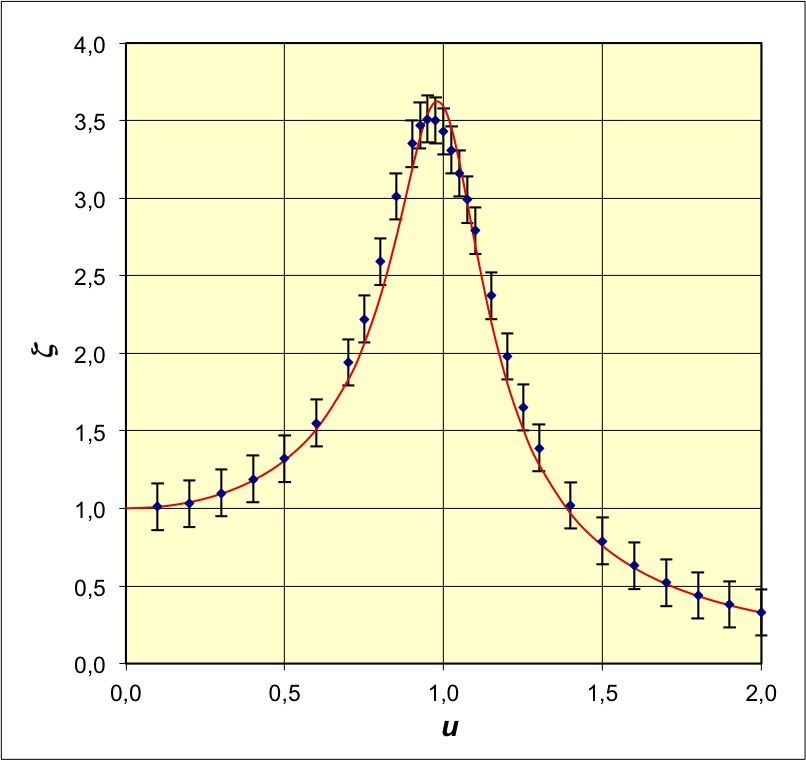
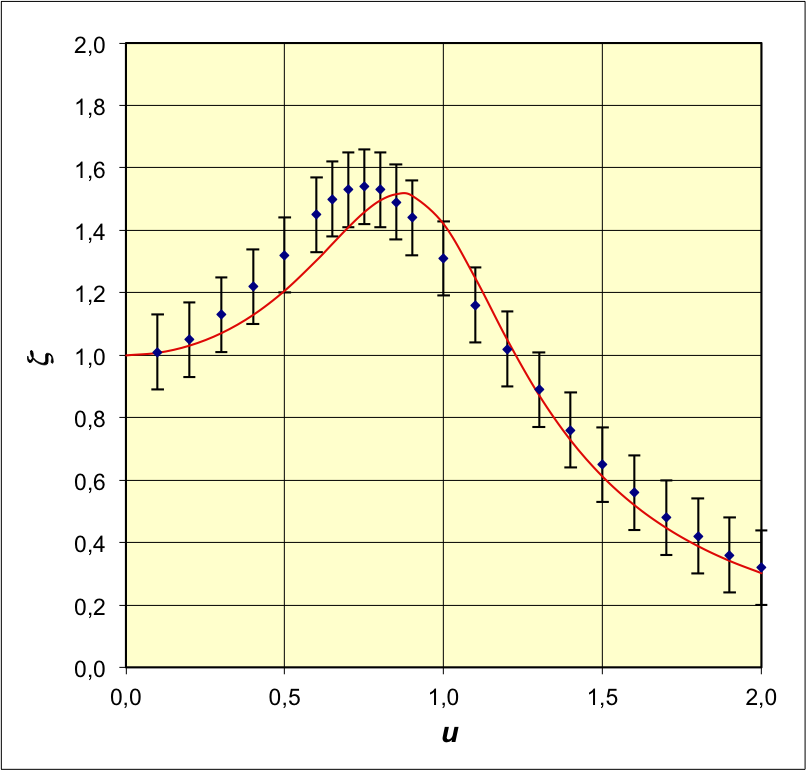
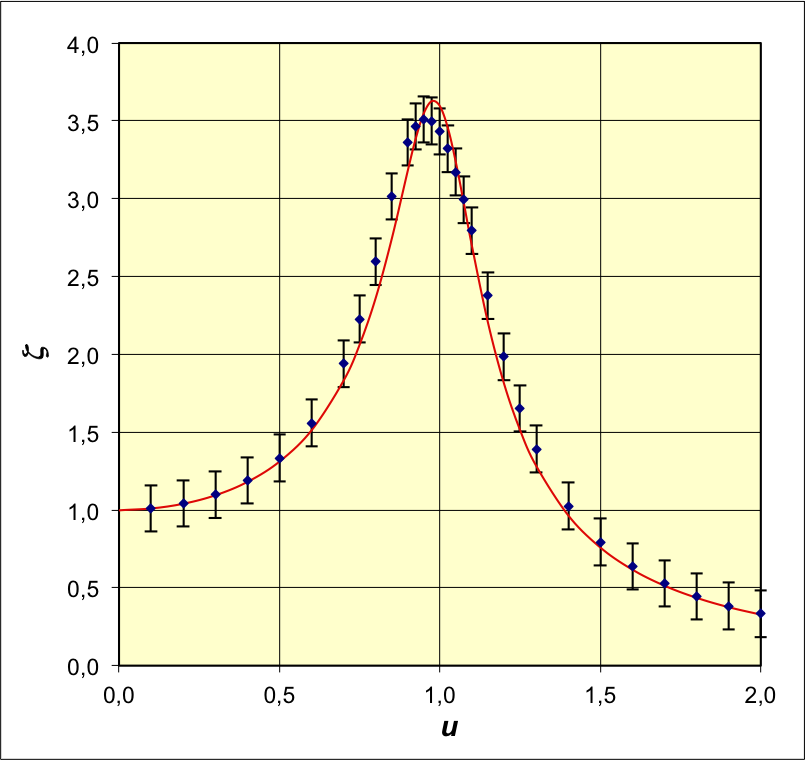
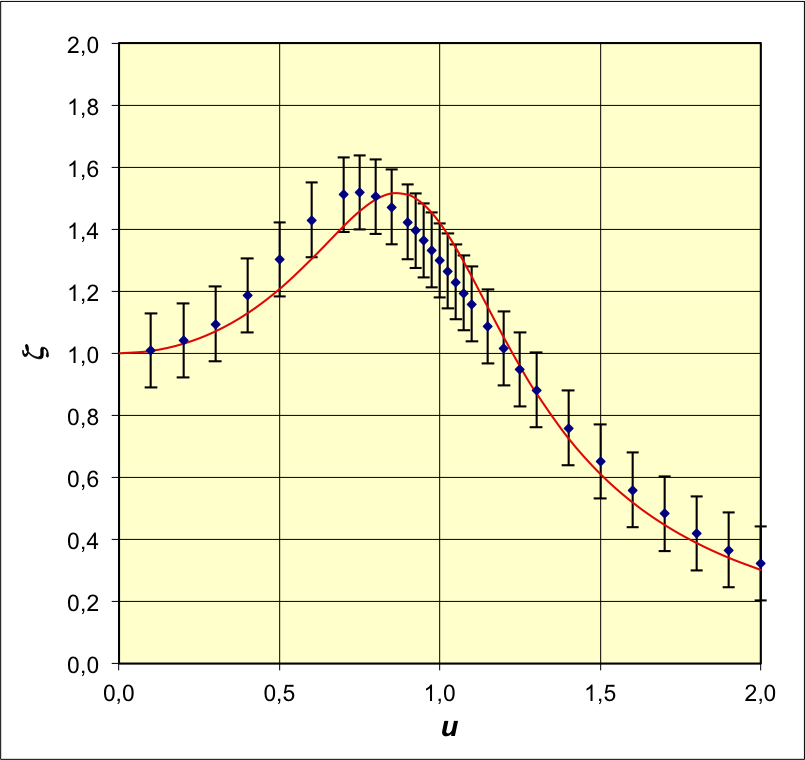
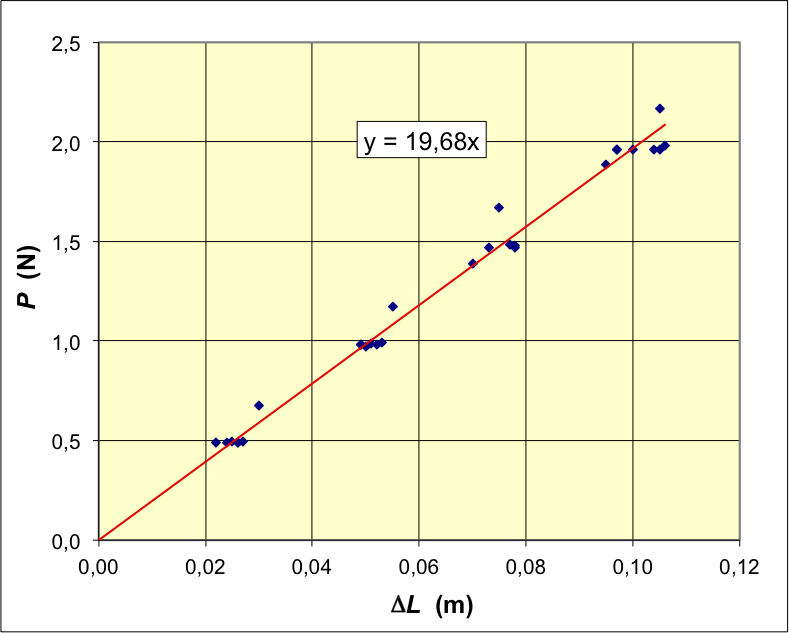
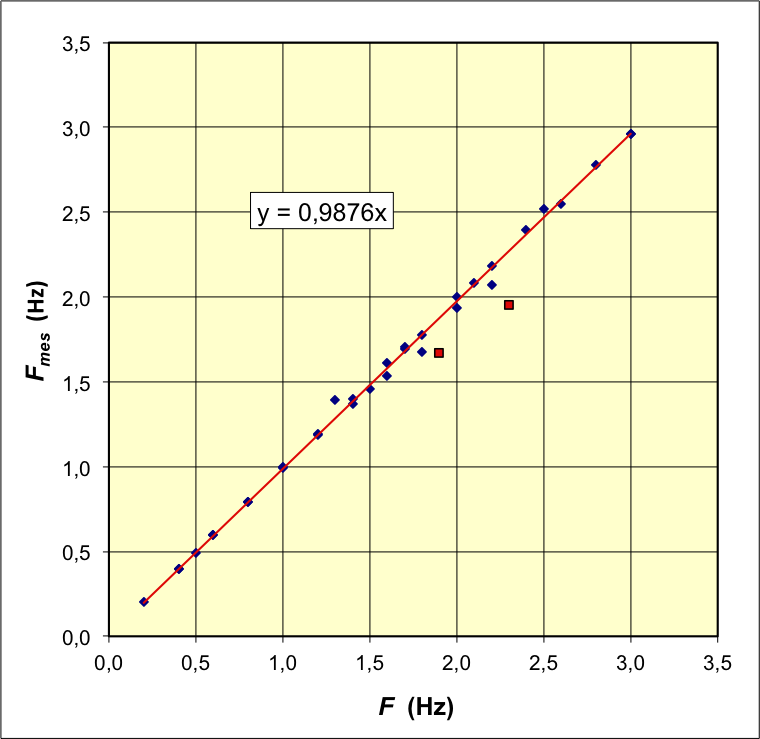
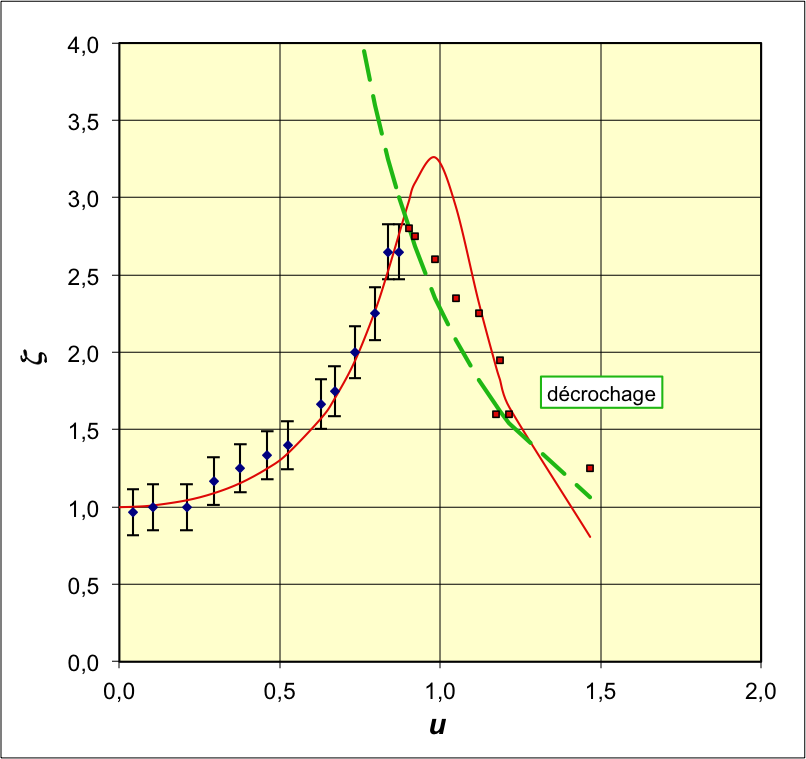
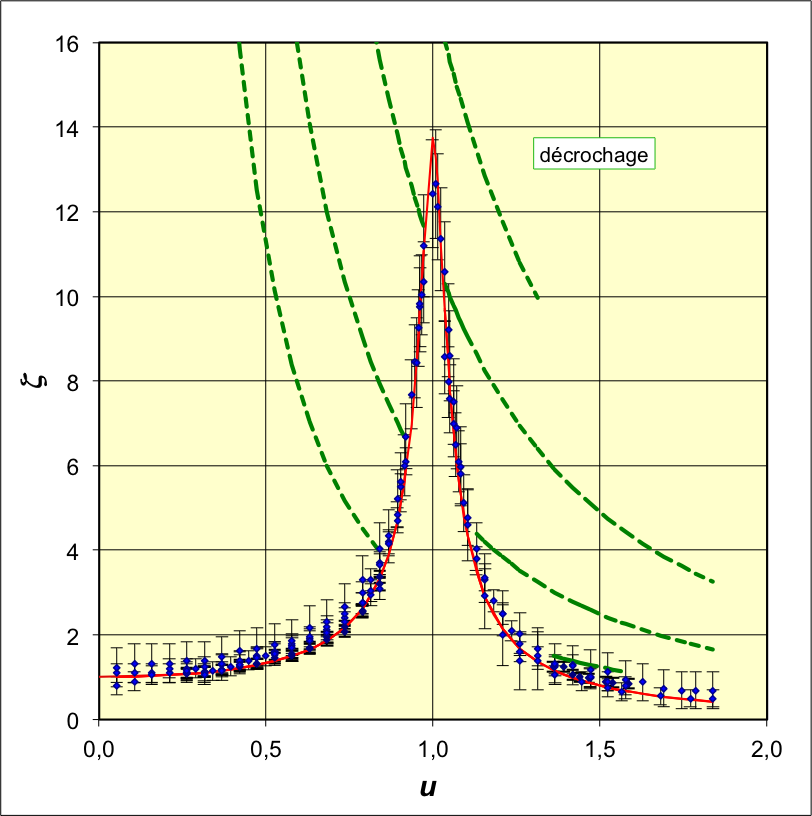
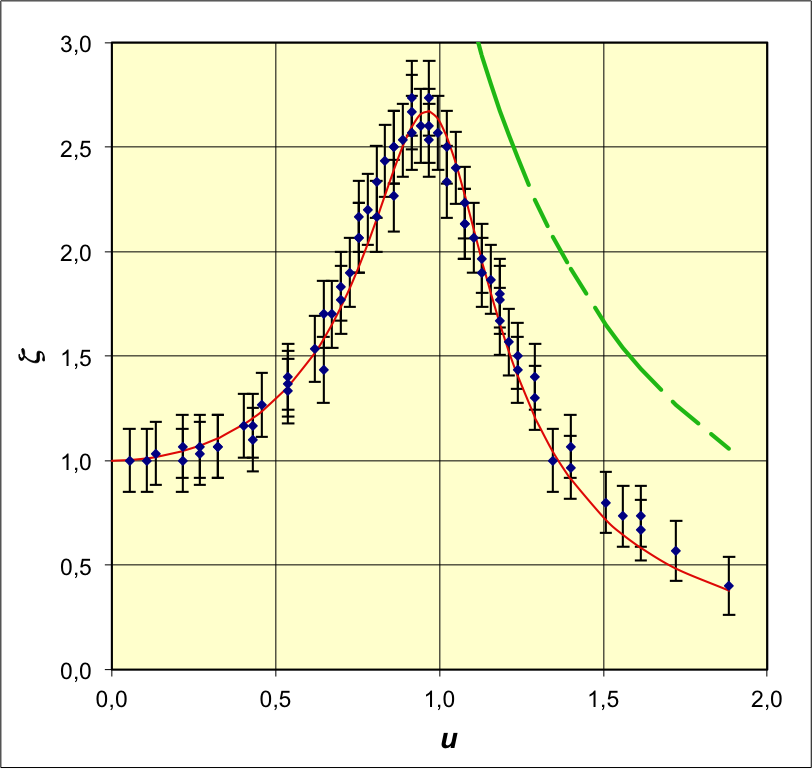
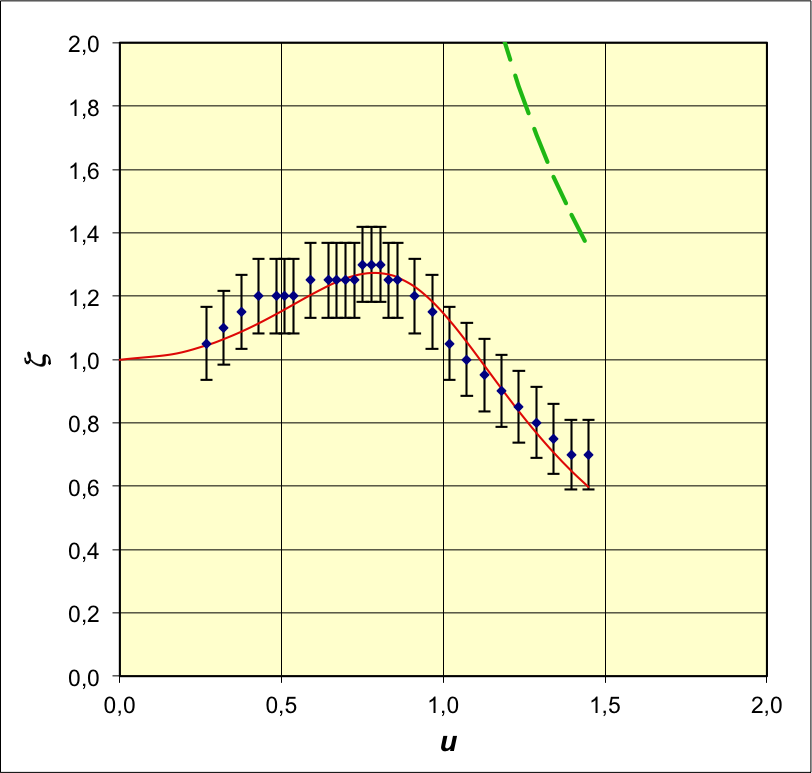
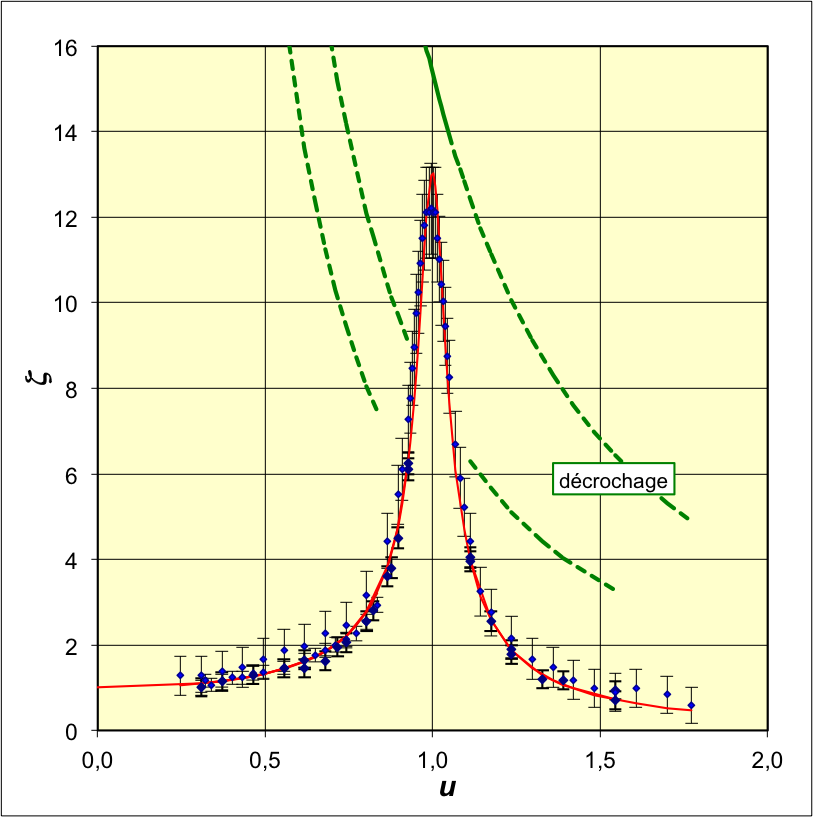
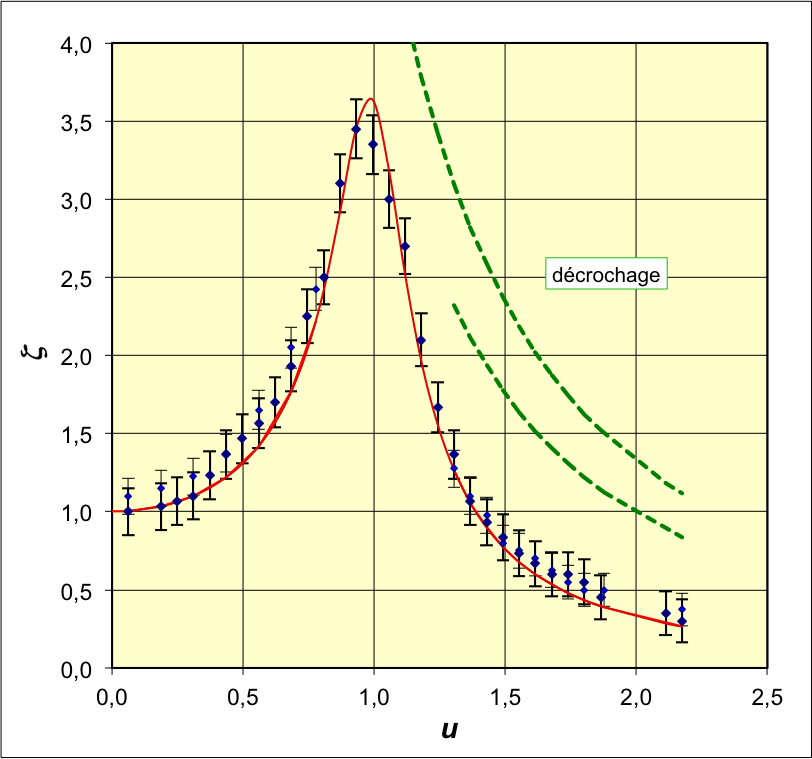
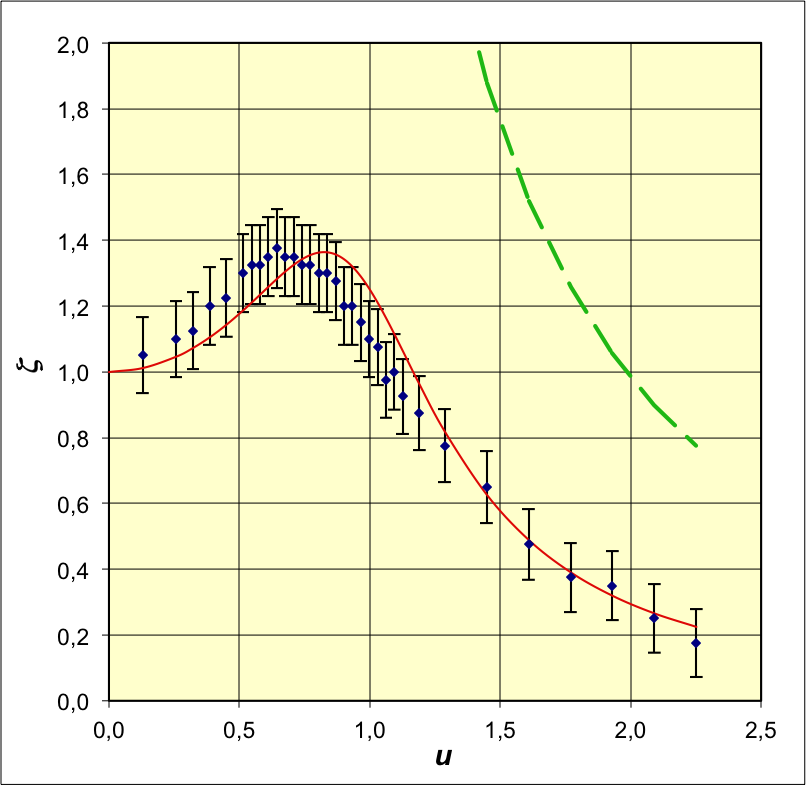
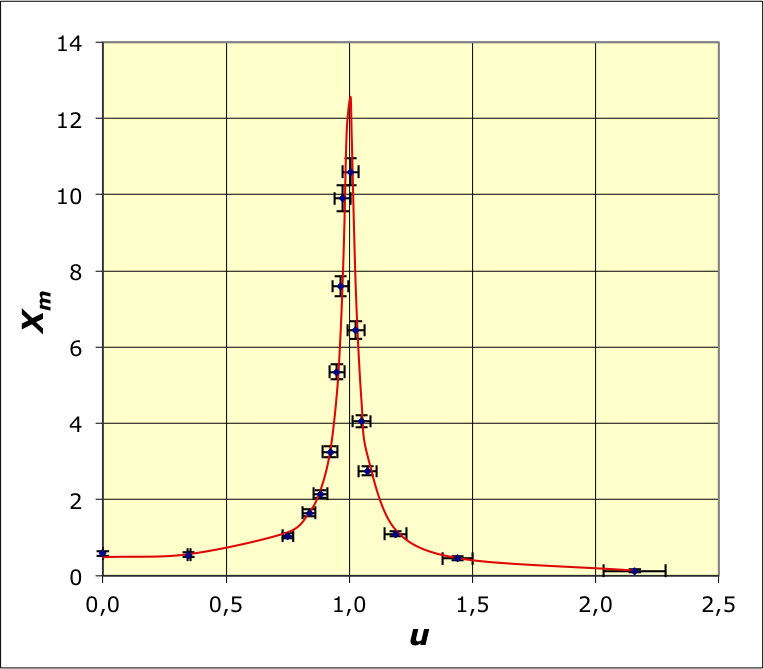
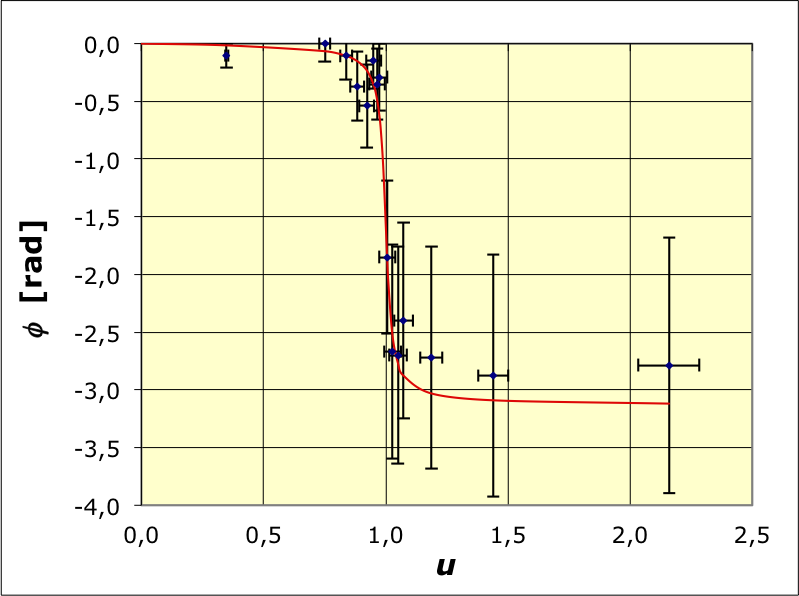
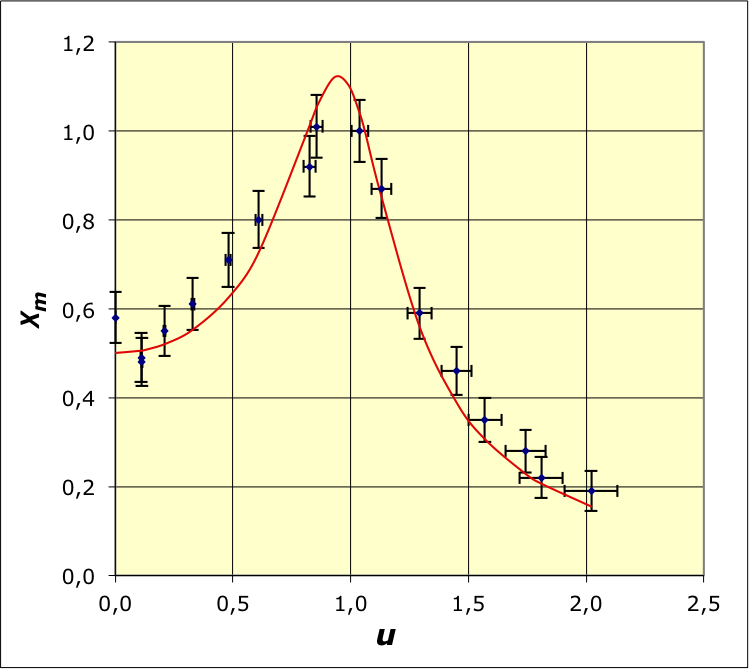
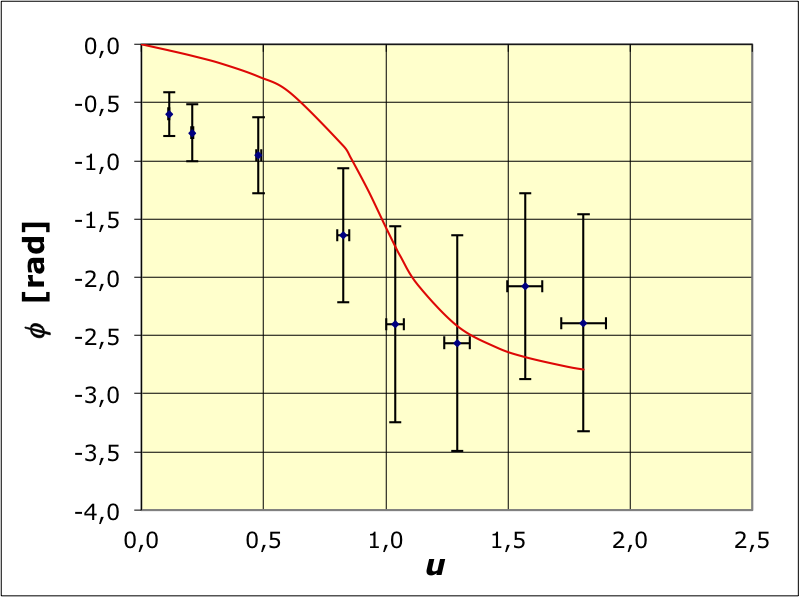
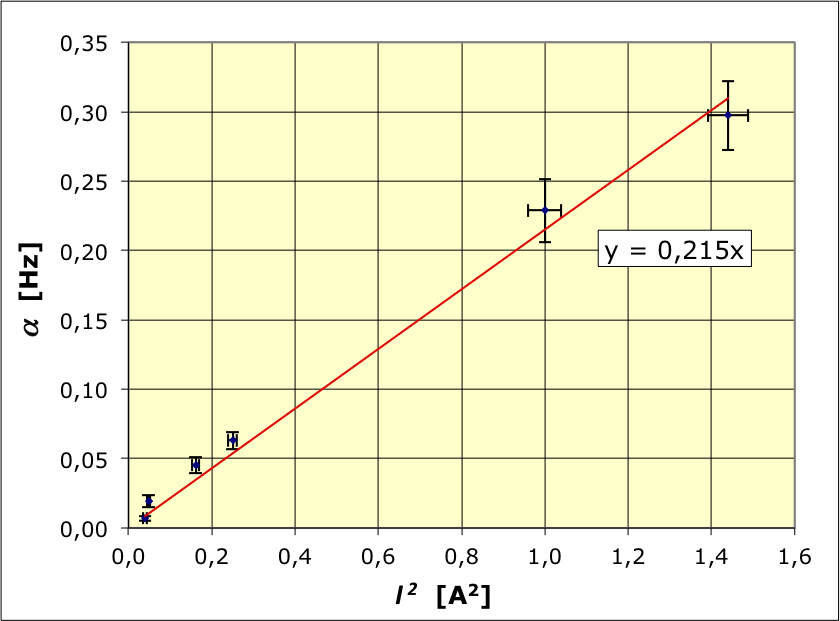
• On utilise un pendule en rotation (pendule de Pohl) comportant :

un disque de cuivre (à évidements) en rotation selon un axe horizontal, avec un moment d'inertie $J$ ;
un ressort spiral de raideur en torsion $C$ , dont une extrémité est fixée au disque et l'autre à un bras articulé lié à un moteur ;
une graduation circulaire avec une unité correspondant à l'amplitude imposée par le moteur ( 50 pour un tour) ; des butées élastiques sont placées aux positions ±20 pour ne pas endommager le montage ;
un électroaimant au bord du disque, causant un freinage par courant de Foucault.

• La constante de torsion du ressort n'a pas été mesurée par les étudiants.

• L'équation du mouvement peut s'écrire sous la forme :

J \:\ddot{θ}+λ \:\dot{θ}+C \:θ=C \:Θ_{Am} \; \cos(ω \:t)

où

λ

est un coefficient de frottement équivalent à l'effet des courants de Foucault. Le comportement en régime permanent est donc

θ=Θ_m\; \cos(ω \:t+ϕ)

analogue à celui d'un oscillateur linéaire, avec ici

\displaystyle ω_0=\sqrt{\frac{C}{J}}

.

• La fréquence propre

N_0

du pendule peut être déterminée en mesurant un nombre suffisant de périodes sans ajouter de frottement électromagnétique (le frottement résiduel est très faible). Les fréquences

N

du moteur sont mesurées de même, puis on raisonne avec

\displaystyle u=\frac{N}{N_0}

.

• Pour chaque fréquence du moteur on attend que le régime soit permanent (effets transitoires amortis, ce qui est moins rapide qu'en électrocinétique) puis on mesure l'amplitude

Θ_m

des oscillations forcées (moyenne des deux côtés) ; on raisonne ensuite avec

\displaystyle X_m=\frac{Θ_m}{Θ_{Am}}

et cela d'autant plus facilement qu'on mesure les angles directement avec une unité correspondant à

Θ_{Am}

.

• Il est aussi possible de mesurer le déphasage (pour chaque fréquence) en chronométrant les instants des passages respectifs par zéro de l'oscillateur (repère blanc) et du moteur (repère noir).

◊ remarque : il faut penser au préalable à régler la position du moteur pour qu'à l'arrêt les deux repères s'alignent à zéro.

◊ remarque : à l'époque des mesures étudiées ici, cela était très peu pratique ; un étudiant donnant les “top” et un autre manipulant un chronomètre ; il serait de nos jours bien plus facile et bien plus précis d'enregistrer une vidéo et de mesurer image par image avec un logiciel approprié.

Courbes de résonance

• Pour une intensité de courant

I=0\text{,}22±0\text{,}01 \:\mathrm{A}

dans l'électro-aimant, on obtient une résonance aiguë.

Les courbes théoriques

\displaystyle X_m=\frac{1}{2 \:\sqrt{\left(1-u^2 \right)^2+2 \:(2 \,α \:u)^2}}

\displaystyle ϕ=\frac{-\arccos\left(1-u^2 \right)}{\sqrt{\left(1-u^2 \right)^2+2 \:(2 \,α \:u)^2}}

ajustées en optimisant le coefficient

\displaystyle α=\frac{λ}{2 \,J}=0\text{,}0191±0\text{,}0043 \:\mathrm{Hz}

donnent une bonne modélisation.

• Pour une intensité de courant

I=1\text{,}00±0\text{,}02\:\mathrm{A}

, on obtient une résonance nettement plus amortie.

Les courbes théoriques ajustées en optimisant le coefficient

α=0\text{,}229±0\text{,}023 \:\mathrm{Hz}

donnent une modélisation correcte, mais les mesures du déphasage sont peu convaincantes.

Modélisation du freinage

• Une série de courbes de résonance ayant été obtenue avec des courants

I

différents, un raisonnement simple permet de tester l'effet des courants de Foucault :

dans l'électro-aimant de courant crée un champ magnétique $B$ proportionnel à $I$ ;
dans le bord du disque métallique de l'oscillateur, en mouvement à la vitesse $v$ par rapport au frein, ce champ magnétique crée un courant induit $i$ proportionnel à $B$ (donc à $I$ ) et à $v$ ;
la circulation du courant $i$ en présence du champ $B$ cause une force de freinage (de Laplace) proportionnelle à $i$ (donc à $I$ et $v$ ) et à $B$ (donc à $I$ ) ;
au total, la force de freinage est proportionnelle à $v$ (moment de force proportionnel à $\dot{θ}$ ) et à $I^2$ ;
ainsi le coefficient de frottement ( $λ$ et/ou $α$ ) est proportionnel à $I^2$ .

La proportionnalité du modèle semble décrire raisonnablement les courbes expérimentales.