M. IV - DYNAMIQUE - OSCILLATIONS LIBRES

Oscillateur harmonique

Définition

• On considère un point matériel dont l’énergie potentielle dépend d’une variable de position

x

; on étudie son comportement au voisinage d’une position d’équilibre stable correspondant à une valeur

x_e

de la variable :

$\displaystyle E_p (x)=E_p (x_e)+(x-x_e) \:\frac{∂E_p}{∂x}(x_e)+\frac{1}{2} {(x-x_e)}^2 \; \frac{∂^2 E_p}{{∂x}^2 }(x_e)+⋯$

L’équilibre stable en

x_e

correspond à un minimum de

E_p

, par suite :

$\displaystyle E_p (x)≈E_p (x_e)+\frac{K}{2}⋅{(x-x_e)}^2$

où le coefficient

\displaystyle K=\frac{∂^2 E_p}{{∂x}^2} (x_e)>0

est nommé “raideur” de l’oscillateur.

◊ remarque : la variable x doit être une longueur, mais le raisonnement peut se généraliser (déplacement proportionnel à un angle, ou autre…).

• Le point est soumis à une force “de rappel” de coordonnée (algébrique) :

\displaystyle F_x=-\frac{∂E_p}{∂x}=-K⋅(x-x_e)

(proportionnalité, selon la loi de Hooke).

En notant

\underline{x}=x-x_e

l'écart à l'équilibre, le mouvement au voisinage est décrit par l’équation :

\ddot{\underline{x}}+ω^2 \: \underline{x}=0

avec la pulsation

\displaystyle ω=\sqrt{\frac{K}{m}}

.

☞ remarque : on peut souvent utiliser l’analogie électro-mécanique :

$q↔x$ (charges déplacées) ; $\displaystyle i=\frac{dq}{dt}↔v=\dot{x}$ ;
$u=R \:i↔F=λ \:v$ (frottement) ; $\displaystyle \frac{1}{C}↔k$ (élasticité) ; $L↔m$ ;
$\displaystyle E_{el}=\frac{q^2}{2 \,C}↔E_{pe}=\frac{1}{2} k \:x^2$ ; $E_{ma}=\frac{1}{2} L \:i^2↔E_c=\frac{1}{2} m \:v^2$ ; ...

Caractéristiques du mouvement

• Les solutions de :

\ddot{x}+ω^2 \: x=0

s'écrivent :

x=A \; \cos(ω \,t)+B \; \sin(ω \,t)

. Les constantes d’intégration sont déterminées par les conditions aux limites, par exemple :

A=x(0)

\displaystyle B=\frac{\dot{x}(0)}{ω}

.

◊ remarque : on peut aussi noter :

x=X_m \; \cos(ω \,t+ϕ)

.

• Pour les petites oscillations, la période

\displaystyle T=\frac{2π}{ω}

ne dépend pas de l’amplitude (propriété d’isochronisme).

• L’énergie mécanique est constante :

$E_m=\frac{1}{2} k \:x^2+\frac{1}{2} m \:\dot{x}^2=\frac{1}{2} m \:ω^2 \: \left(A^2+B^2\right)$ .

Exemple du pendule à ressort vertical

• Pour le pendule à ressort vertical :

E_p=\frac{1}{2} k \:z^2+m \:g \:z

(avec l'origine à la position “à vide”). L’équilibre donne :

\displaystyle \frac{dE_p}{dz}=k \:z+m \:g=0

donc

\displaystyle z_e=-\frac{m \:g}{k}

(équilibre stable car

\displaystyle \frac{d^2 E_p}{{dz}^2} =k>0

◊ remarque : on peut aussi noter

E_p=E_p (z_e)+\frac{1}{2} k \:\underline{z}^2

avec

\displaystyle E_p (z_e)=-\frac{m^2 \: g^2}{2 \,k}

\underline{z}=z-z_e

.

• En dérivant la relation :

E_m=E_c+E_p=Cste

on obtient l’équation du mouvement :

\displaystyle \ddot{z}+\frac{k}{m} \, z=-g

; on peut aussi l'écrire :

\displaystyle \ddot{\underline{z}}+\frac{k}{m} \, \underline{z}=0

.

📖 exercices n° I, II, III et IV.

Oscillateur avec amortissement “solide”

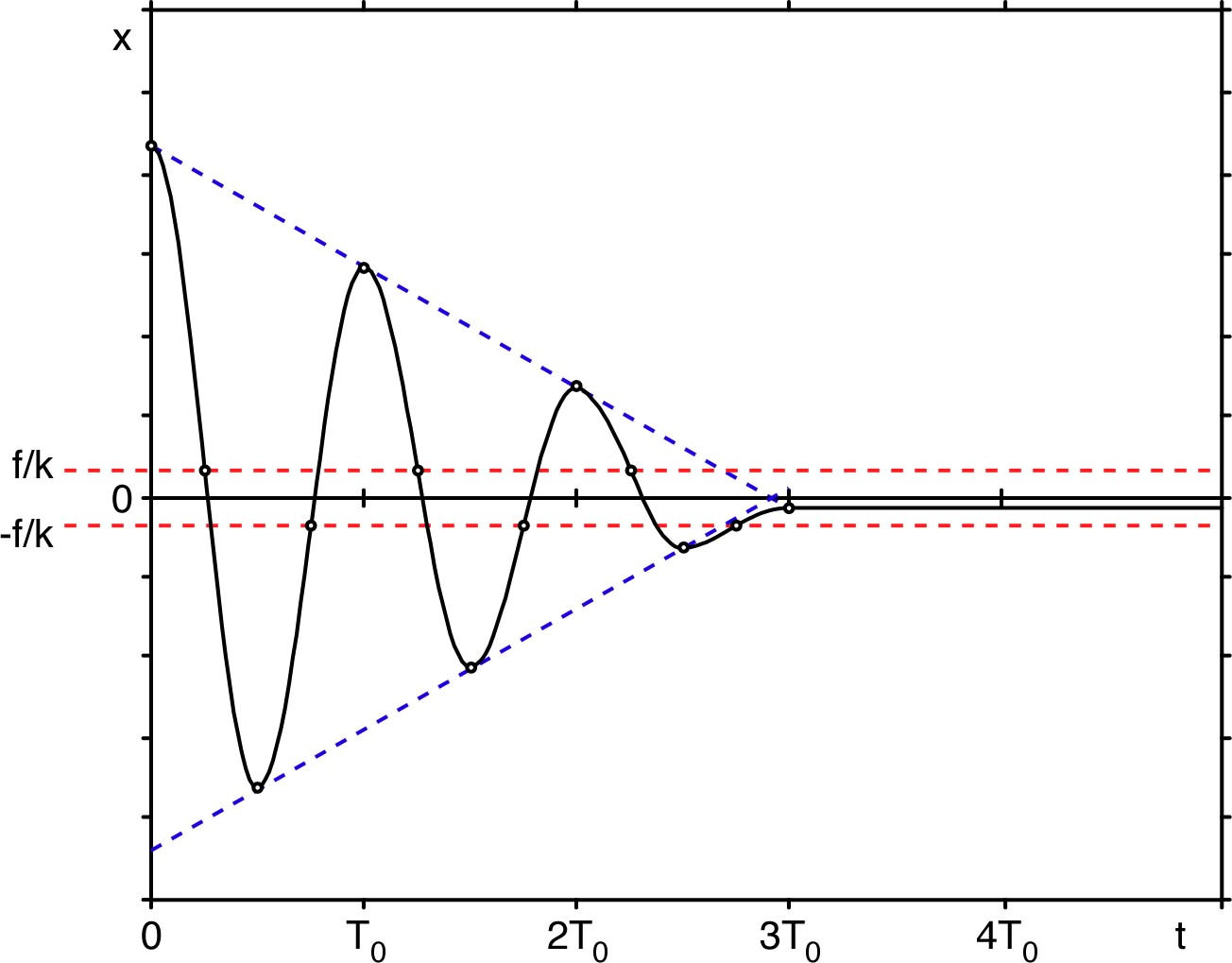
• On considère un pendule à ressort horizontal avec frottement solide (de coefficient

λ

) et on étudie le cas où il y a oscillation (donc glissement).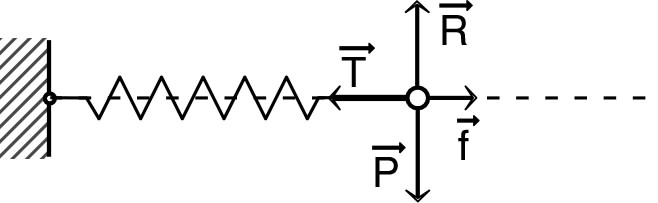

La réaction normale

\overset{→}{R}

du support compense le poids

\overset{→}{P}

(mouvement horizontal) ; par ailleurs, tant qu’il y a glissement, le frottement

f=λ \:R

(selon la direction et le sens contraire du mouvement) est constant (dans ce cas).

• On obtient l’équation différentielle :

m \:\ddot{x}=-k \:x-ε \:f

avec

\displaystyle ε=\frac{\widebar{v}}{v}=\mathrm{sgn}⁡(\widebar{v})

; ceci peut encore s’écrire :

\displaystyle \ddot{x}+ω_0^{\:2} \: x=-\frac{ε \:f}{m}

avec

\displaystyle ω_0=\sqrt{\frac{k}{m}}

.

Pour un départ en

\displaystyle x_0>\frac{f}{m \:ω_0^{\:2}}=\frac{f}{k}>0

à une vitesse initiale nulle, on obtient :

\displaystyle \ddot{x}+ω_0^{\:2} \: x=\frac{f}{m}

puis la solution :

\displaystyle x=\frac{f}{k}+X_m \; \cos(ω_0 \, t)

où

\displaystyle X_m=x_0-\frac{f}{k}>0

.

Pour un “redépart” en

\displaystyle x'_0=2 \, \frac{f}{k}-x_0<-\frac{f}{k}<0

à une vitesse initiale nulle, on obtient :

\displaystyle \ddot{x}+ω_0^{\:2} \: x=-\frac{f}{m}

;

\displaystyle x=-\frac{f}{k}+X'_m \; \cos(ω_0 \, t)

;

\displaystyle X'_m=x_0-3 \:\frac{f}{k}>0

; puis ainsi de suite.

Ceci donne une évolution par raccordement de portions de sinusoïdes décalées, jusqu’à l’arrêt lors du premier passage à vitesse nulle dans l’intervalle

\displaystyle -\frac{f}{k}<x<\frac{f}{k}

.

◊ remarque : le frottement solide est souvent la principale cause d’incertitude des appareils de mesure à aiguille, car il correspond à un “intervalle d’arrêt” dans lequel la position finale est difficilement prévisible.

◊ remarque : la pseudo-période

\displaystyle T_0=\frac{2π}{ω_0}

est l’intervalle entre les passage par

\displaystyle \frac{f}{k}

des portions “descendantes” (ou

\displaystyle -\frac{f}{k}

pour les portions “ascendantes”), ou entre les maximums (ou les minimums) qui sont ici alignés ; par contre, il n’y a pas exactement un décalage

T_0

entre les points de tangence de l’enveloppe (qui n’est d’ailleurs pas exactement rectiligne).

Oscillateur avec amortissement “visqueux”

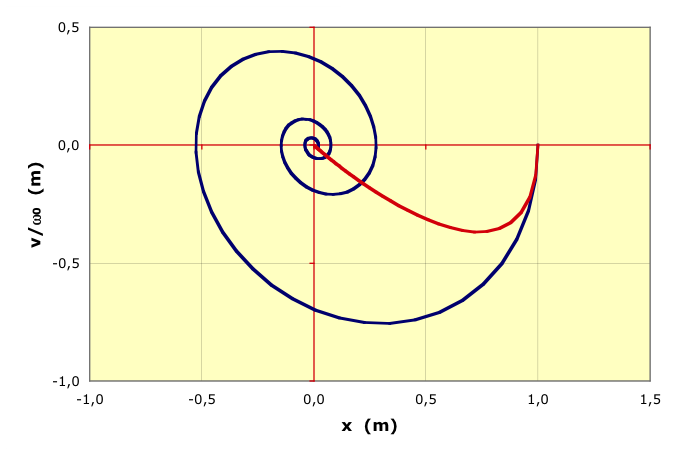
• On considère ici un pendule vertical avec frottement visqueux (le coefficient de frottement est

λ

), réalisé en plongeant la masse

m

dans un liquide.

On peut tenir compte des interactions avec le fluide (poussée d'Archimède...) en “renormalisant” :

la masse : $m\text{’}=m+m_e$ (où $m_e$ est la masse équivalente de fluide “entraîné” avec l'oscillateur) ;
la pesanteur : $\overset{→}{g}\text{’}=\overset{→}{g} \: \frac{m-m_d}{m+m_e}$ (où $m_d$ est la masse de fluide “déplacé” du volume occupé par l'oscillateur).

◊ remarque : pour les expériences usuelles,

m_e≈\frac{1}{2} m_d

; dans la suite, afin de simplifier l'écriture, on note

m

\overset{→}{g}

les quantités renormalisées.

• Avec l'origine à l’extrémité du ressort “à vide” :

m \:\ddot{z}=-m \:g-k \:z-λ \:\dot{z}

; ou bien, en posant

\displaystyle α=\frac{λ}{2 \,m}

\displaystyle ω_0=\sqrt{\frac{k}{m}}

\ddot{z}+2 \,α \:\dot{z}+ω_0^{\:2} \: z=- g

.

En prenant comme origine la position d’équilibre

\displaystyle z_0=-\frac{g}{ω_0^{\:2}}

l’équation devient :

\ddot{z}+2 \,α \:\dot{z}+ω_0^{\:2} \: z=0

.

Cette équation est analogue à celle pour un circuit électrique “RLC” en régime transitoire (

\displaystyle L \:\ddot{q}+R \:\dot{q}+\frac{q}{C}=0

), donc les solutions sont semblables :

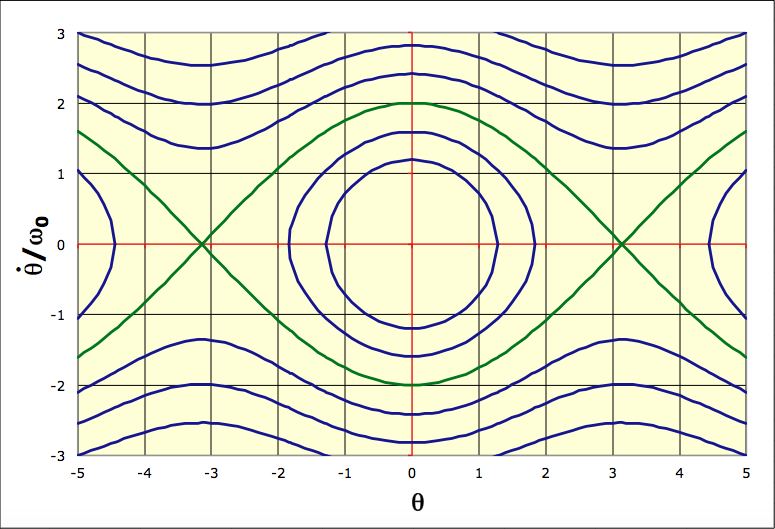
$α^2-ω_0^{\:2}<0$ : régime pseudopériodique, amorti exponentiellement ;
$α^2-ω_0^{\:2}=0$ : régime apériodique “critique” (le plus vite amorti) ;
$α^2-ω_0^{\:2}>0$ : régime apériodique (amorti plus progressivement).

• Ceci peut se visualiser par un diagramme dans “l’espace de phase”, représentant la quantité de mouvement, ou la vitesse, en fonction de la position.

◊ remarque : on peut utiliser

\displaystyle \frac{v}{ω_0}

si on veut une unité de longueur.

Exemple anharmonique : le pendule pesant

• Pour le pendule pesant, l’énergie potentielle peut s'écrire :

E_p=m \:g \:𝓁 .\left[1-\cos(θ)\right]

et l’équilibre correspond à :

\displaystyle \frac{dE_p}{dθ}=m \:g \:𝓁 \; \sin(θ)=0

c’est-à-dire à :

θ_0=0

(équilibre stable pour

\displaystyle \frac{d^2 E_p}{{dθ}^2} =m \:g \:𝓁 \; \cos(θ)>0

).

◊ remarque : au voisinage de l'équilibre on peut écrire

E_p≈E_{p0}+\frac{1}{2} K \:θ^2

avec

E_{p0}=E_p (0)=0

K=m \:g \:𝓁

• En dérivant la relation :

E_m=E_c+E_p=Cste

on obtient ainsi l’équation du mouvement :

\displaystyle \ddot{θ}+\frac{g}{𝓁} \: \sin(θ)=0

, c’est-à-dire :

\displaystyle \ddot{θ}+\frac{g}{𝓁} \: θ≈0

.

On retrouve un oscillateur harmonique pour les petites oscillations, mais la période des grandes oscillations dépend de leur amplitude.

• Pour un pendule à tige (un fil se plierait), l’intégration de l’équation précédente (ou l’énergie mécanique) donne :

\displaystyle \frac{\dot{θ} }{ω_0} =\sqrt{2 \,\left[\cos(θ)-\cos(θ_0)\right]+\left(\frac{\dot{θ}_0}{ω_0} \right)^2\,}

. On en déduit le diagramme de phase suivant :

◊ remarque : le profil d'énergie potentielle et en correspondance avec la “coupe” selon l'axe horizontal du diagramme.

📖 exercices n° V, VI et VII.