DYNAMIQUE - OSCILLATIONS LIBRES - corrigé des exercices

A. EXERCICES DE BASE

Résonateur de Helmholtz

• Si le gaz contenu dans le récipient évolue de façon adiabatique, suivant la loi :

p \:V^γ = p_0 \: V_0^{\:γ}

, on peut écrire en différentiant pour un petit déplacement

dx

\displaystyle \frac{dp}{p}+γ \: \frac{dV}{V}=0

et donc :

\displaystyle \frac{dp}{p}+\frac{γ \:s}{V} \, dx=0

.
• L’effet des forces pressantes de l'air sur les deux faces du piston est par conséquent (algébriquement) :

\displaystyle dF=s \:dp= -\frac{γ \:s^2 \: p}{V} \, dx

. Pour des petites oscillations, on peut considérer en première approximation que :

\displaystyle \frac{γ \:s^2 \: p}{V}≈\frac{γ \:s^2 \: p_0}{V_0}

est quasi-constant ; par suite :

\displaystyle m \:\ddot{x}=F≈-\frac{γ \:s^2 \: p_0}{V_0} \, x

c'est-à-dire :

\displaystyle \ddot{x}+\frac{γ \:s^2 \: p_0}{m \:V_0} \: x≈0

.
• L'équation précédente correspond à un oscillateur harmonique de pulsation :

\displaystyle ω=\sqrt{\frac{γ \:s^2 \: p_0}{m \:V_0}}

et de période :

\displaystyle T=2π \:\sqrt{\frac{m \:V_0}{γ \:s^2 \: p_0}}

.
• Pour les oscillations de l'air contenu dans le goulot, de masse :

m=ρ \:s \:𝓁

, on obtient une fréquence :

\displaystyle N=\frac{1}{2π} \:\sqrt{\frac{γ \:s \:p_0}{ρ \:𝓁 \:V_0}}

(avec

ρ≈1\text{,}23 \:\mathrm{g.L^{-1}}

la masse volumique moyenne usuelle de l'air).

Oscillation au voisinage d'un équilibre

• En l’absence de frottement, la réaction

\overset{→}{R}

de la surface est perpendiculaire au mouvement et ne travaille pas. Compte tenu des conditions initiales (vitesse nulle), la somme des forces reste dans un plan vertical (celui qui contient le poids, la position initiale, la réaction

\overset{→}{R}

initiale ; c’est donc par symétrie une section méridienne). Le mouvement se fait donc dans ce plan méridien et on peut décrire la position du point matériel à l’aide d’une seule coordonnée, par exemple son abscisse

x

.
• En décrivant la pesanteur par l’énergie potentielle

E_p=m \:g \:y=m \:g \:a \:x^2

, l’équation du mouvement découle de la conservation de

E_m=E_c+E_p

avec

E_c=\frac{1}{2} m .\left(\dot{x}^2+\dot{y}^2 \right)=\frac{1}{2} m \:\dot{x}^2 \: \left(1+4 \,a^2 \: x^2 \right)

. On obtient ainsi :

\displaystyle \frac{\dot{E}_m}{m \:\dot{x}}=\ddot{x} .\left(1+4 \,a^2 \: x^2 \right)+2 \,a \:x .\left(g+2 \,a \: \dot{x}^2 \right)=0

(en supposant

\dot{x}≠0

puisqu’on étudie le mouvement et non l’équilibre).
☞ remarque : ce type de raisonnement suppose que l'énergie ne dépend que d'une seule variable de position ; puisqu'on utilise la variable

x

on doit donc substituer

y=y(x)

.
• Dans la mesure où cette équation est compliquée, on peut commencer par raisonner sur les propriétés générales du mouvement. Ainsi, il existe une position d’équilibre stable au “fond” du bol : minimum de l’énergie potentielle.
• Par ailleurs, puisque l’énergie cinétique ne peut pas être négative, le mobile ne peut pas remonter plus haut que sa position initiale, donc son mouvement est limité. Or il se déplace sur une courbe (intersection du bol avec le plan méridien contenant le mouvement) donc le mouvement correspond soit à un mouvement périodique (repassant par les mêmes positions dans les mêmes conditions, donc forcément périodique), soit à un mouvement tendant asymptotiquement vers une position d’équilibre.
• En pratique, le poids entraîne le mobile vers le bas et ce dernier “accélère” tant qu’il descend (

E_c

augmente quand

E_p

diminue) ; il atteint donc le “fond” du bol avec une vitesse maximum et il passe de l’autre côté sans pouvoir s’arrêter. De l’autre côté, il “ralentit” au fur et à mesure qu’il remonte et retrouve sa hauteur initiale, avec une vitesse nulle, après une durée de remontée égale par symétrie à la durée de descente... et ainsi de suite, donc le mouvement est périodique.
• Pour les petites oscillations (au voisinage de l’équilibre), on peut simplifier en :

\ddot{x}+2 \,a \:g \:x ≈0

et on en déduit que le mouvement est sinusoïdal, de période :

\displaystyle T=\frac{2π}{\sqrt{2 \,a \:g}}

.
◊ remarque : pour simplifier l’expression de

E_c

on peut envisager de repérer la position par l’abscisse curviligne

s

le long de la courbe parcourue, qui correspond à :

\dot{s}=\widebar{v}

donc :

s=∫\,\left(1+4 \,a^2 \: x^2 \right) \: dx

; avec l’intégration par partie, on obtient :

\displaystyle s=\frac{x}{2} \, \sqrt{1+4 a^2 x^2}-\frac{1}{2 \,a} \, \mathrm{arsinh}(2 \,a \:x)

d'intérêt limité car cela complique l’expression de

E_p

; pour les petites oscillations, on peut toutefois écrire

E_c=\frac{1}{2} m \:\dot{s}^2

et développer

E_p (s)

s≈x .\left(1-\frac{2}{3} \,a^2 \: x^2 \right)

;

x≈s .\left(1+\frac{2}{3} \,a^2 \: s^2 \right)

;

E_p≈m \:g \:a \:s^2 \:\left(1+\frac{4}{3} \,a^2 \: s^2 \right)

; le terme d’ordre le plus bas montre qu’il y a un équilibre stable pour

s=0

et une “raideur”

K=2 \,m \:g \:a

donnant des petites oscillations de période

\displaystyle T=2π \:\sqrt{\frac{m}{K}}=\frac{2π}{\sqrt{2 \,a \:g}}

; le terme d’ordre suivant permet éventuellement une étude des plus grandes oscillations par développement limité.

Oscillateur anharmonique et dilatation

• L’énergie potentielle

E_p=\frac{1}{2} k \:x^2-\frac{1}{3} k \:s \:x^3

donne

\displaystyle \frac{dE_p}{dx}=k \:x-k \:s \:x^2

donc

\displaystyle \frac{dE_p}{dx} (0)=0

(extremum) ce qui correspond à un équilibre ; mais la condition

k \:x .(1-s \:x)=0

indique qu’il existe une autre position d’équilibre pour

\displaystyle x=\frac{1}{s}

.
• Par ailleurs

\displaystyle \frac{d^2 E_p}{{dx}^2} =k-2 \,k \:s \:x

donc

\displaystyle \frac{d^2 E_p}{{dx}^2} (0)=k>0

(minimum) ce qui correspond à un équilibre stable ; mais la condition

k .(1-2 \,s \:x)=-k<0

pour

\displaystyle x=\frac{1}{s}

indique que l’autre position d’équilibre est instable (maximum de

E_p

).
• La courbe représentative est la suivante :

dynOscLibres_cor_Im/dynOscLibres_cor_Im1.jpg

• Compte tenu de la forme de la courbe précédente, on voit que le mouvement reste au voisinage de

x=0

seulement si

\displaystyle x≤\frac{1}{s}

(la force

\displaystyle \widebar{F}=-\frac{dE_p}{dx}

exerce un “rappel” vers l’origine tant que le mobile ne sort pas du “creux”).
• L’équation du mouvement peut s’écrire :

\displaystyle m \:\ddot{x}=\widebar{F}= -\frac{dE_p}{dx}=-k \:x .(1-s \:x)

. Cette équation n’étant pas simple (terme quadratique), il est alors intéressant d’utiliser un développement limité pour

\displaystyle x≪\frac{1}{s}

• Pour

\displaystyle x≪\frac{1}{s}

on obtient à l’ordre le plus bas l’équation simplifiée

m \:\ddot{x}+k \:x≈0

qui donne alors la solution :

x=A \; \cos(ω_0 \: t)

avec

\displaystyle ω_0=\sqrt{\frac{k}{m}}

et avec une origine des temps appropriée. Ceci correspond effectivement à la solution du mouvement pour les très petites amplitudes, c’est-à-dire

\displaystyle A≪\frac{1}{s}

.
• À l’ordre suivant, on peut chercher une solution de la forme :

x=A .\left[\cos(ω_0 \: t)+ε \:f(t)\right]

avec

ε≪1

(pour décrire une correction d’ordre supérieur) et

f(t)

inconnue décrivant la forme du terme correctif.
• En substituant dans l’équation et en simplifiant par

A

(avec

A≠0

pour le mouvement), on obtient :

m .\left[-ω_0^{\:2} \; \cos(ω_0 \: t)+ε \:\ddot{f} \right]+k . \left[\cos(ω_0 \: t)+ε \:f \right] \: \left\{1-s \:A . \left[\cos(ω_0 \: t)+ε \:f \right]\right\}=0

. En limitant au premier ordre en

ε

s \:A

, on obtient :

\displaystyle \ddot{f}+ω_0^{\:2} \: f=ω_0^{\:2} \: \frac{s \:A}{ε} \: \cos^2(ω_0 \: t)=ω_0^{\:2} \: \frac{s \:A}{2 \,ε} \: \left[1+\cos(2 \,ω_0 \: t) \right]

.
• Ceci donne des oscillations forcées de pulsation

2 \,ω_0

autour d’une valeur moyenne

\displaystyle f_0=\frac{s \:A}{2 \,ε}

. Si on veut écrire la solution sous la forme :

f=\cos(2 \,ω_0 \: t)+a

, on obtient :

\displaystyle ε=-\frac{s \:A}{6}

\displaystyle a=\frac{s \:A}{2 \,ε}=-3

• Les valeurs moyennes des cosinus sont nulles et il reste :

\displaystyle ⟨\,x\,⟩=A \:ε\; ⟨\,f\,⟩=A \:ε \:a=\frac{s \:A^2}{2}

.
• Si on suppose qu’on peut appliquer le principe d’équipartition de l’énergie à l’oscillateur anharmonique, dans la limite des petites oscillations, on obtient :

⟨\,E_p\,⟩≈\frac{1}{2} k \;\,x^2\,⟩≈\frac{1}{2} k_B \: T

.
• De

\left⟨\, \cos^2(ω_0 \: t)\,\right⟩=\frac{1}{2}

on déduit (à l’ordre le plus bas) :

\displaystyle ⟨\,E_p\,⟩≈\frac{k \:A^2}{4}

et donc :

\displaystyle A^2≈\frac{2 \,k_B \: T}{k}

. En reportant alors dans le terme d’ordre suivant, on obtient :

\displaystyle ⟨\,x\,⟩≈\frac{s \:k_B \: T}{k}

, ce qui correspond à un allongement proportionnel à la température (dilatation).

Oscillation au voisinage d'un équilibre

1.a.	• En repérant la position sur le cercle par l’angle $θ$ , proportionnel au déplacement, les coordonnées de $M$ par rapport au centre du cercle sont $x=R \: \sin(θ)$ et $y=R \: \cos(θ)$ . On peut donc exprimer la longueur sous la forme : $L(θ)=\sqrt{x^2+(D+R-y)^2}=\sqrt{\left(R \:\sin(θ) \right)^2+\left(D+R-R \:\cos(θ) \right)^2}$ .

1.b.	• La masse $m$ est soumise à une réaction du cercle, mais cette force ne travaille pas et peut être omise dans les raisonnements sur l'énergie. • L'énergie potentielle élastique peut s'écrire : $E_{pe}=\frac{1}{2} k .\left[L(θ)-L_0 \right]^2$ ; l’énergie potentielle de pesanteur est : $E_{pp}=m \:g \:z = m \:g \:R \; \cos(θ)$ . • L’énergie mécanique peut s'écrire : $E_m=\frac{1}{2} m \:R^2 \: \dot{θ}^2+\frac{1}{2} k . \left[L(θ)-L_0 \right]^2+m \:g \:R \; \cos(θ)$ . • Les positions d’équilibre correspondent à : $\displaystyle \frac{dE_p}{dθ}=k \:R \; \sin(θ) \: \left(\left(1-\frac{L_0}{L(θ)} \right)\,(D+R)-\frac{m \:g}{k}\right)=0$ . • Il y a donc un équilibre pour $\sin(θ)=0$ , ce qui se limite à $θ=0$ si on suppose que le cercle est très incomplet (comme le suggère le schéma de l'énoncé), sinon il y a aussi $θ=π$ . • Il peut exister deux autres positions d’équilibre pour $θ_e$ tel que : $\displaystyle L(θ_e )=L_e=L_0 \, \frac{D+R}{D+R-\frac{m \:g}{k}}$ si cette longueur est supérieure à $D$ et inférieure à (au plus) $D+2 \,R$ (le mobile $M$ reste sur le cercle de rayon $R$ , même s'il est complet, or l’expression précédente tend vers l’infini quand $\displaystyle \frac{m \:g}{k}→D+R$ ). • La condition pour obtenir ainsi $L_e>D$ correspond à $\displaystyle \left(1-\frac{L_0}{D}\right)\, (D+R)-\frac{m \:g}{k}<0$ (c'est à dire que le poids doit être suffisant pour imposer un décalage en haut). • La condition pour obtenir ainsi $L_e<D+2\,R$ correspond à $\displaystyle \left(1-\frac{L_0}{D+2\,R}\right)\, (D+R)-\frac{m \:g}{k}>0$ (c'est à dire que la tension du ressort doit être suffisante pour imposer un décalage en bas). • D'après l'expression de $L(θ)$ , ces équilibres correspondent à : $\displaystyle \cos(θ_e )=\frac{R^2+(D+R)^2-L_e^{\:2}}{2 \,R.(D+R)}$ .

1.c.	• Chaque équilibre est stable si et seulement s'il correspond à une dérivée seconde positive : $\displaystyle \frac{d^2 E_p}{{dθ}^2} =k \:R \; \cos(θ) \: \left(\left(1-\frac{L_0}{L(θ)} \right)\,(D+R)-\frac{m \:g}{k}\right)+k \:R \; \sin(θ) \: \left(\frac{L_0}{[L(θ)]^3} \: (D+R)^2 \: R \;\sin(θ) \right)>0$ . • Pour l’équilibre en $θ=0$ on obtient : $\displaystyle \left(1-\frac{L_0}{D}\right)\, (D+R)-\frac{m \:g}{k}>0$ , c’est-à-dire que cet équilibre est stable si $L_e<D$ (poids insuffisant) et instable sinon. ◊ remarque : pour l’équilibre en $θ=π$ on obtient : $\displaystyle \left(1-\frac{L_0}{D+2\,R}\right)\, (D+R)-\frac{m \:g}{k}<0$ , c’est-à-dire que cet équilibre est stable si $L_e>D+2\,R$ (tension du ressort insuffisante) et instable sinon. • Pour les équilibres en $θ_e≠0$ (ou $π$ ) on obtient (en simplifiant) : $\displaystyle \frac{L_0}{[L(θ)]^3} \: \sin^2(θ)>0$ , ce qui est toujours vrai, c'est-à-dire que ces équilibres sont toujours stables s'ils existent.

1.d.	• L’équation du mouvement découle de la propriété : $\displaystyle \frac{dE_m}{dt}=\dot{θ} \: \frac{dE_m}{dθ}=0$ ; l’étude du mouvement correspondant à $\dot{θ}≠0$ . • Compte tenu de $v=R \:\dot{θ}$ , l'énergie cinétique est $E_c=\frac{1}{2} m \:R^2 \: \dot{θ}^2$ ; l’équation du mouvement est (pour les petites oscillations au voisinage de $θ=0$ ) : $\displaystyle \frac{dE_m}{dθ}≈m \:R^2 \: \ddot{θ}+K' \:θ=0$ avec un “coefficient de raideur” : $\displaystyle K'=\frac{d^2 E_p}{{dθ}^2} =k \:R .\left(\left(1-\frac{L_0}{D}\right)\,(D+R)-\frac{m \:g}{k}\right)>0$ . • Dans ce cas (dérivation par rapport à $θ$ ) la constante $K'$ ainsi obtenue n'est pas ce qu'on appelle conventionnellement “raideur” de l’oscillateur. La raideur est en fait $\displaystyle K=\frac{K'}{R^2} =k .\left(1-\frac{L_0}{D}\right)\, \left(1+\frac{D}{R}\right)-\frac{m \:g}{k}$ intervenant dans l'équation exprimée en fonction du déplacement $R \:θ$ : $m \;\ddot{\overbrace{(R \:θ)}}+K .(R \:θ)=0$ . • La période des petites oscillations est donc : $\displaystyle T≈2π \:\sqrt{\frac{m \:R^2}{K'}}=2π \:\sqrt{\frac{m}{K}}$ .

2.a.	• On obtient : $\displaystyle L(θ)=\frac{D}{\cos(θ)} =-\frac{x}{\sin(θ)}$ .

2.b.	• La masse $m$ est soumise à une réaction de la tige inclinée, mais cette force ne travaille pas et peut être omise dans les raisonnements sur l'énergie. • L'énergie potentielle élastique peut s'écrire : $E_{pe}=\frac{1}{2} k .\left[L(θ)-L_0 \right]^2$ ; l’énergie potentielle de pesanteur est : $E_{pp}=m \:g \:z=m \:g \:x \; \sin(α) = -m \:g \:D \; \sin(α) \; \tan(θ)$ . • L’énergie mécanique peut s'écrire : $E_m=\frac{1}{2} m \:\dot{x}^2+\frac{1}{2} k . \left[L(θ)-L_0 \right]^2-m \:g \:D \; \sin(α) \; \tan(θ)$ . • Les positions d’équilibre correspondent à : $\displaystyle \frac{dE_p}{dθ}=\frac{k \:D \:L_0}{\cos^2(θ)} \: \left(\left(\frac{L(θ)}{L_0} -1\right) \: \sin(θ)-\frac{m \:g \;\sin(α)}{k \:L_0}\right)=0$ ; elles sont donc solution de l'équation : $\tan(θ)=\sin(θ)+λ$ .

2.c.	• Puisque la pente minimale de $\tan(θ)$ est égale à $1$ et que la pente maximale de $\sin(θ)$ est égale à $1$ , la différence entre les deux est strictement croissante et ne peut prendre une valeur $λ$ que pour au plus une valeur de $θ$ . Par ailleurs $\tan(θ)$ peut prendre toute valeur réelle et $\sin(θ)$ est bornée, donc la différence peut prendre toute valeur $λ$ pour au moins une valeur de $θ$ . • Ceci peut être visualisé à l'aide du graphique suivant, mettant en particulier en évidence la solution $θ=1\text{,}08 \:\mathrm{rad}=62 \,°$ dans le cas où $λ=1$ .

2.d.	• L’équilibre est stable si et seulement s'il correspond à une dérivée seconde positive : $\displaystyle \frac{d^2 E_p}{{dθ}^2} =\frac{k \:D \:L_0}{\cos^2(θ)} \: \left(\frac{1}{\cos^2(θ)} -\cos(θ) \right)>0$ (en simplifiant $\tan(θ)-\sin(θ)-λ$ ). • Ceci se ramène à $\cos^3(θ)<1$ ce qui est toujours vrai (la pesanteur y impose toujours $θ>0$ ).

2.e.	• L’équation du mouvement découle de la propriété : $\displaystyle \frac{dE_m}{dt}=\dot{θ} \; \frac{dE_m}{dθ}=0$ ; l’étude du mouvement correspondant à $\dot{θ}≠0$ . • Compte tenu de $\displaystyle v=-\frac{D}{\cos^2(θ)} \: \dot{θ}$ , l'énergie cinétique est $\displaystyle E_c=\frac{1}{2} m \: \frac{D^2}{\cos^4(θ)} \; \dot{θ}^2$ ; l’équation du mouvement est (pour les petites oscillations au voisinage de $θ=0$ ) : $\displaystyle \frac{dE_m}{dθ}≈m \: \frac{D^2}{\cos^4(θ_e )} \; \ddot{θ}+K' .(θ-θ_e )=0$ avec un “coefficient de raideur” : $\displaystyle K'=\frac{d^2 E_p}{{dθ}^2} =\frac{k \:D^2}{\cos^4(θ_e )} \left(\frac{1}{\cos^2(θ_e )} -\cos(θ_e ) \right)>0$ . • Dans ce cas (dérivation par rapport à $θ$ ) la constante $K'$ ainsi obtenue n'est pas ce qu'on appelle conventionnellement “raideur” de l’oscillateur. La raideur est en fait $\displaystyle K=\frac{K' \:\cos^4(θ_e )}{D^2} =k .\left[1-\cos^3(θ_e ) \right]$ intervenant dans l'équation exprimée en fonction du déplacement $x$ : $m \:\ddot{x}+K .(x-x_e)=0$ . • La période des petites oscillations est ainsi : $\displaystyle T=2π \:\sqrt{\frac{m}{K}}$ .

Amortissement et viscosité

• En supposant le mouvement limité à l’axe vertical et en prenant comme origine la position “à vide” de l’extrémité du ressort (l’ordonnée

z

est alors égale à l’allongement du ressort), la relation fondamentale de la dynamique peut s’écrire algébriquement :

m \:\ddot{z}=-m \:g-k \:z-λ \:\dot{z}

avec

λ=6π \:η \:r

.
• Ceci peut s’écrire sous la forme :

\ddot{z}+2 \,α \:\dot{z}+ω_0^{\:2} \: z=-g

avec

\displaystyle α=\frac{λ}{2 \,m}

\displaystyle ω_0=\sqrt{\frac{k}{m}}

. La solution particulière

\displaystyle z_e=-\frac{g}{ω_0^{\:2}}=-\frac{m \:g}{k}

montre alors que le mouvement s’effectue “autour” de cette position limite (position d’équilibre). En changeant d’origine pour se ramener à cet équilibre, l’équation devient plus simplement :

\ddot{z}+2 \,α \:\dot{z}+ω_0^{\:2} \: z=0

.
• Si

α<ω_0

le mouvement est pseudopériodique, de la forme :

z=\mathrm{e}^{-α \,t} \; \left[A \;\cos(ω \:t)+B \;\sin(ω \:t) \right]

avec

ω=\sqrt{ω_0^{\:2}-α^2}

. On obtient ainsi :

\displaystyle α=2π \: \frac{\sqrt{T^2-T_0^{\:2}}}{T_0 \: T}=\frac{λ}{2 \,m}=\frac{3π \:η \:r}{m}

\displaystyle η=\frac{2 \,m}{3 \,r} \, \frac{\sqrt{T^2-T_0^{\:2}}}{T_0 \: T}

.
• Le décrément logarithmique est

δ=α \:T

(après une pseudo-période, la partie sinusoïdale reprend la même valeur et la variation du logarithme correspond à

\ln\left[\mathrm{e}^{-α \,T} \right]

). D’après ce qui précède, on obtient donc :

\displaystyle δ=2π \: \frac{\sqrt{T^2-T_0^{\:2}}}{T_0} =\frac{3π \:η \:r \:T}{m}

Amortissement et facteur de qualité

• L’équation de l’oscillateur considéré est de la forme :

\ddot{x}+2 \,α \:\dot{x}+ω_0^{\:2} \: x=0

. Pour un amortissement faible (

α<ω_0

), les solutions s'écrivent :

x=X_m \: \mathrm{e}^{-α \,t} \; \cos(ω \:t+ϕ)=\mathrm{e}^{-α \,t} \: \left[A \;\cos(ω \,t)+B \;\sin(ω \,t) \right]

avec :

ω=\sqrt{ω_0^{\:2}-α^2}

.
• L’énergie mécanique de l’oscillateur est :

E_m=\frac{1}{2} m \:\dot{x}^2+\frac{1}{2} k \:x^2

où

m

est le coefficient d’inertie de l’oscillateur et où

k=m \:ω_0^{\:2}

est sa “raideur”. Pour un amortissement faible

α≪ω_0

ω≈ω_0

(à l’ordre le plus bas). On obtient alors :

\dot{x}≈-ω_0 \: X_m \: \mathrm{e}^{-α \,t} \: \sin(ω \:t+ϕ)

E_m (t)≈\frac{1}{2} m \:ω_0^{\:2} \: X_m^{\:2} \: \mathrm{e}^{-2α \,t}

.
• L’énergie perdue par “période” est :

$∆E_m=E_m (t)-E_m (t+T)≈E_m (t)\: \left(1-\mathrm{e}^{-2α \,t} \right) ≈ 2 \,α \:T \:E_m = 2 \,δ \:E_m$ .

• Le facteur de qualité peut alors s’écrire :

\displaystyle Q=\frac{ω_0}{2 \,α}=\frac{2π \:E_m}{∆E_m}≈\frac{π}{δ}

.
◊ remarque : on peut aussi exprimer le facteur de qualité comme le rapport

\displaystyle \frac{X_{mM}}{X_0}

pour des oscillations forcées à la résonance, selon l’équation :

\ddot{\underline{x}}+2 \,α \:\dot{\underline{x}}+ω_0^{\:2} \: \underline{x}=ω_0^{\:2} \: X_0 \; \mathrm{e}^{\mathrm{j}ωt}

(en notations complexes) et la solution :

\underline{x}=X_m \: \mathrm{e}^{\mathrm{j} \,(ωt+ϕ)}

donnant

\displaystyle X_m=\frac{ω_0^{\:2} \: X_0}{\sqrt{\left(ω_0^{\:2}-ω^2 \right)^2+4 \,α^2 \: ω^2}}

(et un déphasage qui importe peu ici) ; pour un amortissement faible, l’amplitude maximum correspond à

ω≈ω_0

et donc :

\displaystyle X_{mM}≈X_0 \: \frac{ω_0}{2 \,α}

; le facteur de qualité est ainsi :

\displaystyle 𝒬=\frac{X_{mM}}{X_0} ≈\frac{ω_0}{2 \,α}

et on retrouve bien

\displaystyle 𝒬≈\frac{π}{δ}

si on utilise la notation des régimes transitoires

\displaystyle δ=α \:T=\frac{2π \:α}{ω}≈\frac{2π \:α}{ω_0}

(pour un amortissement faible).

2.	• L’amortissement indiqué correspond à : $\mathrm{e}^{n \:α \:t}=\mathrm{e}^{n \:δ}=10$ et donc : $\displaystyle 𝒬≈\frac{π}{δ}=\frac{n \:π}{\ln(10)} ≈1\text{,}36 \:n$ .

Diagrammes de phase

a.	• La solution peut s’écrire : $x=X_m \: \cos(ω_0 \, t+ϕ)$ et $\displaystyle \frac{\dot{x}}{ω_0} =- X_m \: \sin(ω_0 \, t+ϕ)$ . • Le diagramme de phase correspond donc à un cercle de rayon $X_m$ .

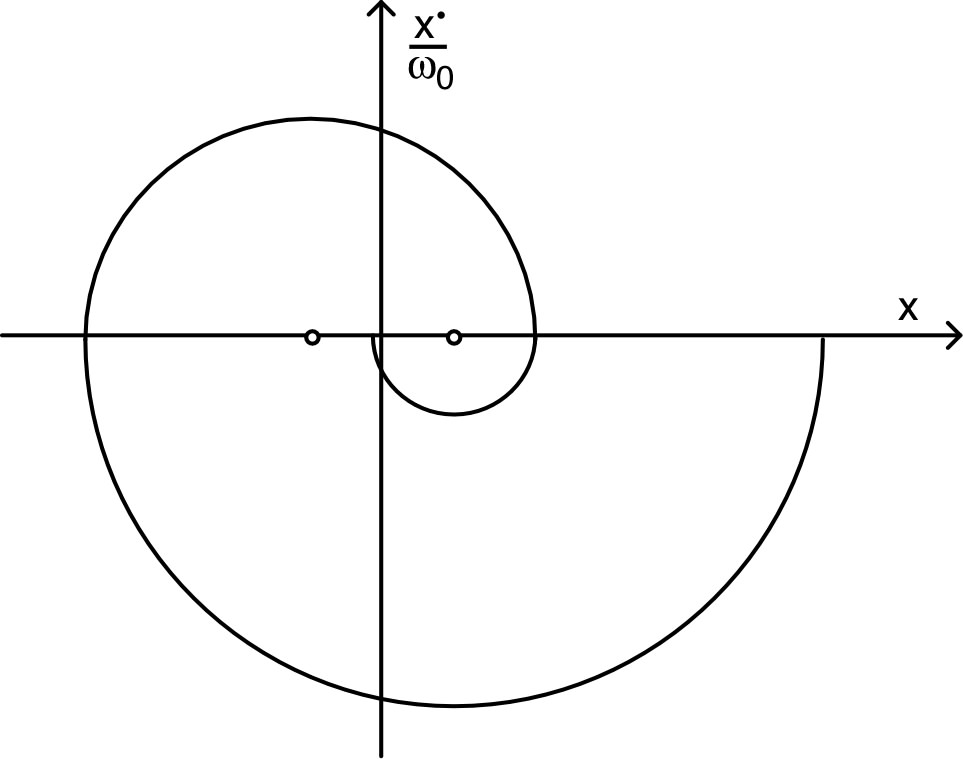
• Pour un départ à vitesse nulle, la première alternance donne :

$\displaystyle x=\frac{f}{k}+X_m \: \cos(ω_0 \, t)$ ;
$\displaystyle \frac{\dot{x}}{ω_0} =- X_m \: \sin(ω_0 \, t)$ .

La portion correspondante du diagramme de phase est donc un demi-cercle de rayon

X_m

et de centre

\displaystyle x_C=\frac{f}{k}

.
• De même la deuxième alternance donne :

$\displaystyle x=-\frac{f}{k}+X'_m \: \cos(ω_0 \, t)$ ;
$\displaystyle \frac{\dot{x}}{ω_0} =-X'_m \: \sin(ω_0 \, t)$ .

La portion correspondante du diagramme de phase est donc un demi-cercle de rayon

X'_m

et de centre

\displaystyle x'_C=-\frac{f}{k}

.
• On poursuit ainsi en raccordant les demi-cercles (avec arrêt dès que l’intersection avec l’axe des

x

est entre

\displaystyle \frac{f}{k}

\displaystyle -\frac{f}{k}

dynOscLibres_cor_Im/dynOscLibres_cor_Im2.jpg

• L’équation est semblable par rapport à la variable

θ

, mais un peu moins simple :

\ddot{θ}+ω_0^{\:2} \; \sin(θ)=0

avec

\displaystyle ω_0=\sqrt{\frac{g}{𝓁}}

. La solution approchée pour les petites oscillations correspond à l’oscillateur harmonique. La solution exacte n’est pas facilement explicitable, mais il suffit ici de la relation entre

θ

\dot{θ}

.
• L’intégration de l’équation précédente (ou le théorème de l’énergie mécanique) permet d’écrire :

$\displaystyle \frac{\dot{θ}}{ω_0} =\sqrt{2 \,\left[\cos(θ)-\cos(θ_0 ) \right]+\left(\frac{\dot{θ}_0}{ω_0} \right)^2}$ .

• On en déduit le diagramme de phase ci-après.
◊ remarque : pour les petites oscillations au voisinage de l’origine, on retrouve le diagramme de phase correspondant à un cercle de rayon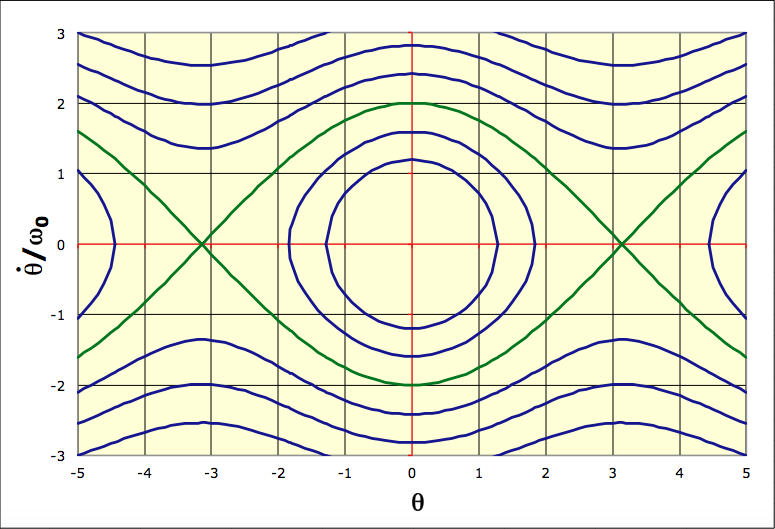

Θ_m

B. EXERCICES D’APPROFONDISSEMENT

Amortissement par courants de Foucault

• Si le cadre monte d'une hauteur

dz

le flux magnétique coupé par le fil du haut est

dϕ=B \:A \:dz

. Il apparaît une force électromotrice induite :

\displaystyle e=-\frac{dϕ}{dt}=-B \:A \:\dot{z}

et un courant induit :

\displaystyle i=\frac{e}{R}=-\frac{B \:A}{R} \, \dot{z}

.
◊ remarque : il apparaît aussi un champ magnétique induit qui s'ajoute au champ magnétique initial, mais cet effet est du second ordre et peut être négligé.
• Le courant induit cause une force de Laplace sur le fil du haut ; cette force, selon la loi de Lenz, tend à s'opposer au mouvement qui la provoque :

\overset{→}{F}=i \:\overset{→}{A}×\overset{→}{B}

soit algébriquement :

\displaystyle F=-\frac{B^2 \: A^2}{R} \: \dot{z}

.
◊ remarque : il y a aussi des forces de Laplace sur les fils des côtés, mais elles se compensent.
• L'équation différentielle du mouvement s’écrit donc :

\displaystyle m \:\ddot{z}=-m \:g-k .(z-z_0)-\frac{B^2 \: A^2}{R} \: \dot{z}

et l'équilibre correspond à :

0=-m \:g-k .(-z_0)

d'après le choix de l'origine ; donc :

\displaystyle \ddot{z}+\frac{B^2 \: A^2}{m \:R} \: \dot{z}+\frac{k}{m} \, z=0

.
• Cette équation est de la forme :

\ddot{z}+2 \,α \:\dot{z}+ω_0^{\:2} \: z=0

où

\displaystyle α=\frac{B^2 \: A^2}{2 \,m \:R}

\displaystyle ω_0=\sqrt{\frac{k}{m}}

. Les solutions peu amorties (

α<ω_0

) sont de la forme :

z=Z_m \: \mathrm{e}^{-α \,t} \; \cos(ω \:t+ϕ)

où

ω=\sqrt{ω_0^{\:2}-α^2}

.
• Le décrément logarithmique décrit la décroissance de l'amplitude sur une pseudo-période

\displaystyle T=\frac{2π}{ω}

\displaystyle δ=\ln\left(\frac{z_n}{z_{n+1}} \right)=α \:T=\frac{2π \:α}{\sqrt{ω_0^{\:2}-α^2}}≈\frac{2π \:α}{ω_0} =\frac{π \:B^2 \:A^2}{R \:\sqrt{m \:k}}

(amortissement très faible).

Oscillateur à trois dimensions

• La condition d’équilibre stable en

M_0

correspond alors à :

\overset{→}{∇}E_p=\overset{→}{0}

K_i>0

(en général, il y a des “raideurs” différentes selon les trois axes). On simplifie alors en choisissant l’origine du repère à la position d’équilibre :

E_p (M)≈E_p (O)+\frac{1}{2} {\displaystyle ∑_i \left(K_i \: x_i^{\:2} \right)}

2.a.	• Dans ces conditions, le point $M$ est soumis à une force “de rappel” : $\overset{→}{F}=-\overset{→}{∇}E_p=-∑_i \left(K_i \: x_i \: \overset{→}{u}_i \right)$ où $\overset{→}{u}_i$ est le vecteur unitaire selon $Ox_i$ . • On en déduit les équations : $\ddot{x}_i+ω_i^{\:2} \: x_i=0$ avec $\displaystyle ω_i=\sqrt{\frac{K_i}{m}}$ ; les solutions peuvent s’écrire sous la forme : $x_i=X_{im} \: \cos(ω_i \, t+ϕ_i )$ , mais ceci correspond a priori à trois oscillations indépendantes : le mouvement est en général non périodique si les $K_i$ sont indépendants ! ◊ remarque : on peut obtenir l’équation du mouvement en dérivant l’énergie mécanique (constante) : $E_m=∑_i \left(\frac{1}{2} m_i \: \dot{x}_i^{\:2}+\frac{1}{2} K_i \: x_i^{\:2} \right)$ ; cette méthode met en évidence le fait que chacune des contributions des différentes coordonnées à $E_m$ est constante (les directions des axes ont été choisies ainsi).

2.b.	• Le cas particulier avec $K_1=K_2=K_3$ (noté $K$ ) correspond à : $E_p (M)≈E_p (O)+\frac{1}{2} K \:\overset{⟶}{OM}^2$ et à une force centrale : $\overset{→}{F}=-\overset{→}{∇}E_p=-K \;\overset{⟶}{OM}$ . • En notant $\overset{→}{r}=\overset{⟶}{OM}$ pour simplifier, on en déduit l’équation : $\ddot{\overset{→}{r}}+ω^2 \; \overset{→}{r}=\overset{→}{0}$ avec $\displaystyle ω=\sqrt{\frac{K}{m}}$ ; les solutions peuvent s’écrire sous la forme : $\overset{→}{r}=\overset{→}{A} \; \cos(ω \:t)+\overset{→}{B} \; \sin(ω \:t)$ et les conditions initiales imposent : $\overset{→}{A}=\overset{→}{r}(0)$ et $\displaystyle \overset{→}{B}=\frac{\overset{→}{v}(0)}{ω}$ . ◊ remarque : la notation avec déphasages est ici moins pratique, car les $ω_i$ sont égaux, mais les $ϕ_i$ sont différents. • On obtient donc ici un mouvement plan : dans le plan de $\overset{→}{A}$ et $\overset{→}{B}$ . ◊ remarque : conformément à l’étude générale des mouvements à force centrale, le plan du mouvement est perpendiculaire au moment cinétique $\overset{→}{σ}_O$ . • On peut alors montrer qu’il est toujours possible de choisir la direction des axes de coordonnées de telle façon que : $x=X_m \: \cos(ω \:t)$ ; $y=Y_m \: \sin(ω \:t)$ ; $z=0$ ; ce qui correspond à une trajectoire elliptique ayant son centre à l’origine (et non pas un foyer, contrairement aux forces en $\displaystyle \frac{1}{r^2}$ ). ◊ remarque : ce choix d'axes n’est pas contradictoire avec celui envisagé précédemment pour éliminer les termes croisés $\displaystyle \frac{∂^2 E_p}{∂x_i ∂x_{j≠i}}(M_0 ) .\left(x_i-x_{i0} \right)\left(x_j-x_{j0} \right)$ ; en effet, par symétrie, ces termes s’annulent si les $K_i$ sont égaux (les seules directions privilégiées sont alors celles découlant des conditions initiales).