OSCILLATIONS MÉCANIQUES LIBRES - corrigé du TP


Oscillations en translation ; mouvement

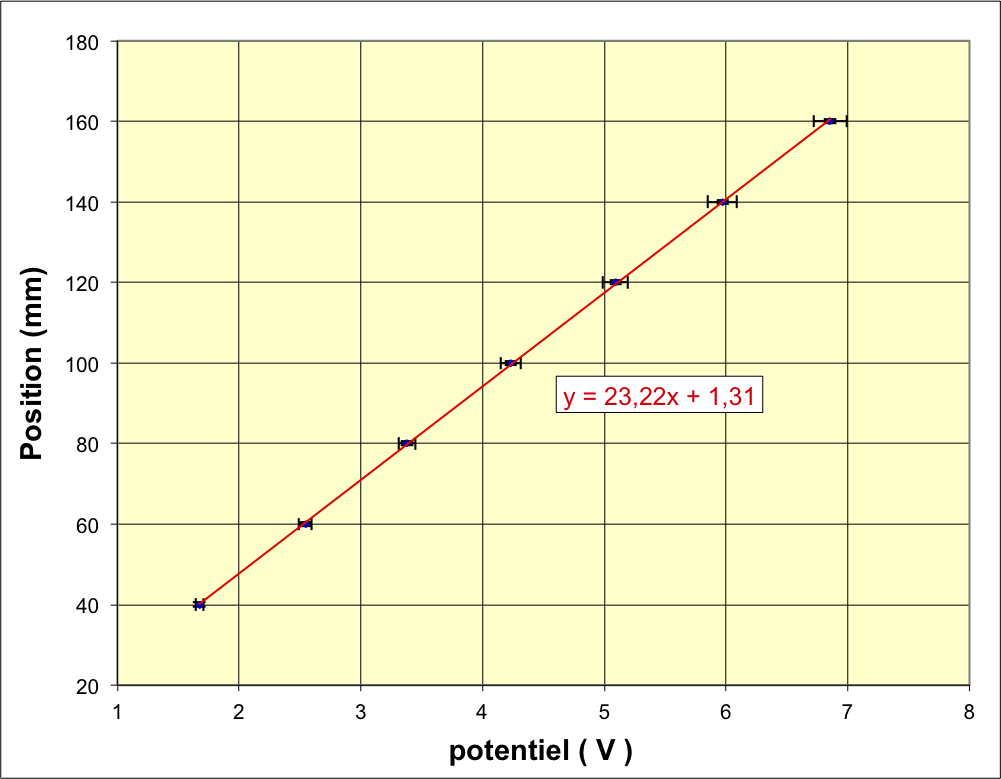
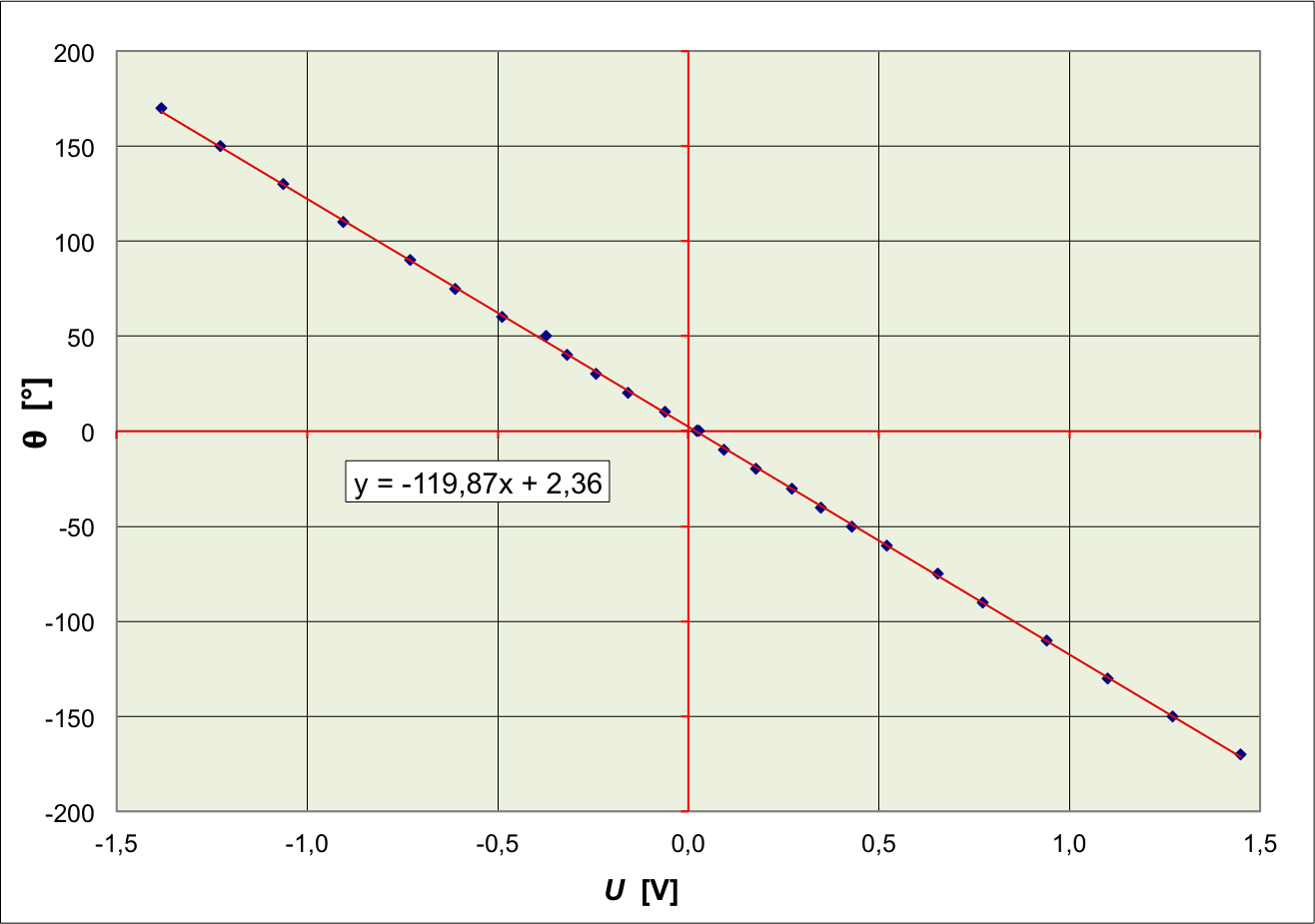
Étalonnage de la cuve

◊ remarque : peu d'indications sont imposées dans le protocole du TP, afin d'entraîner l'ingéniosité et les capacités de communication des étudiants.

• On “remplit” la cuve d'eau : pour les cuves verticales jusqu'un peu au dessus de l'électrode supérieure ; pour les cuves horizontales ≈1cm≈1 \:\mathrm{cm}  suffit.

Les cuves verticales sont des éprouvettes graduées : on peut utiliser les repères en mL\mathrm{mL} ou mesurer l'équivalence en cm\mathrm{cm} . Pour les cuves horizontales (transparentes), le plus simple est de fixer préalablement dessous une feuille de papier millimétré.

• On mesure alors, en fonction de la position, le potentiel électrique de l'électrode mobile (faisant partie de l'oscillateur) par rapport à une électrode servant de référence (logiquement celle de la cuve au potentiel le plus bas). Les mesures doivent couvrir toute la zone des mouvements étudiés ensuite.

On obtient généralement une variation très bien décrite par une modélisation affine (cela simplifie la “traduction” ultérieure des tensions en positions, mais ce n'est pas indispensable).

dynOscLibres_corTP_Im/etalonnage.png

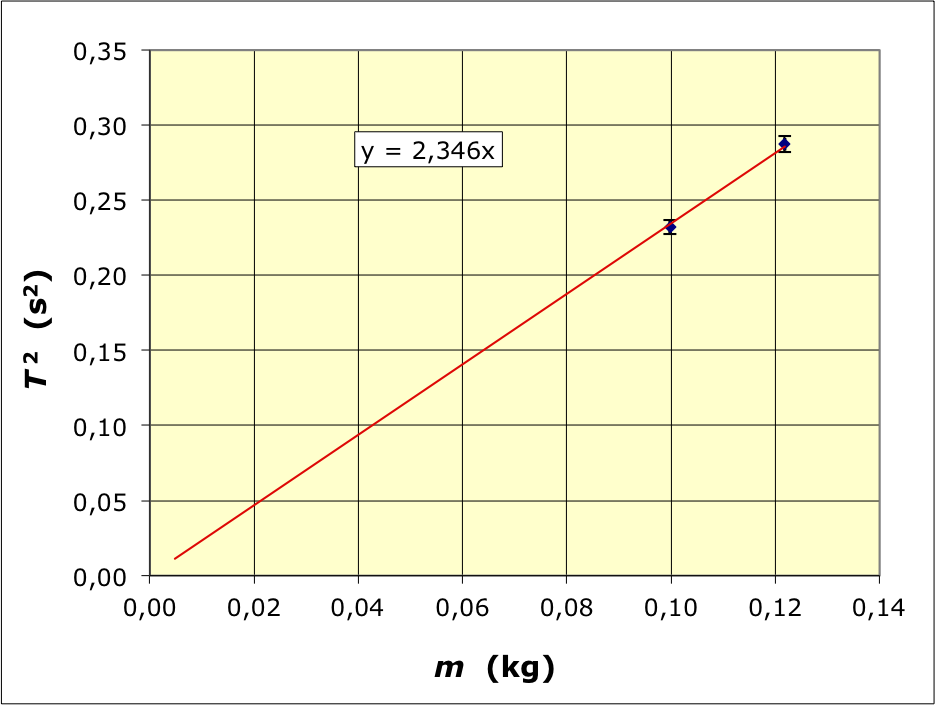
Influence de la masse et de la raideur

• Pour de faibles amortissements, on peut considérer  ω≈ω0ω≈ω_0 .  On peut même se limiter à chronométrer visuellement une dizaine de (pseudo)périodes pour un oscillateur dépourvu de dispositif d'enregistrement (il en faut tout de même un nombre suffisant pour obtenir une précision satisfaisante).

Bien que hélas trop peu nombreuses, les mesures confirment que  T2T^2  est proportionnel à  mm  selon un coefficient  2,35±0,05s2.kg−12\text{,}35±0\text{,}05 \:\mathrm{s^2.kg^{-1}}  compatible avec  4π2k=2,27±0,03s2.kg−1\displaystyle \frac{4π^2}{k}=2\text{,}27±0\text{,}03 \:\mathrm{s^2.kg^{-1}} .

dynOscLibres_corTP_Im/masse.png

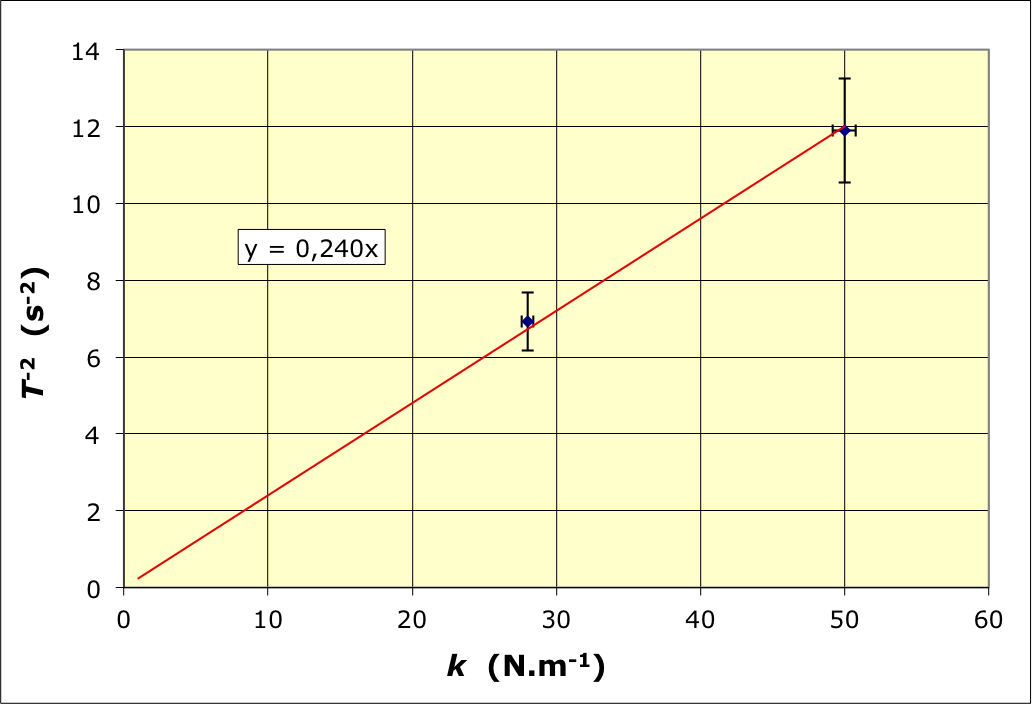
Malgré une précision insuffisante, on vérifie de même que  T−2T^{-2}  est proportionnel à  kk  selon un coefficient  0,240±0,025kg−10\text{,}240±0\text{,}025 \:\mathrm{kg^{-1}}  compatible avec  14π2m=0,225±0,02kg−1\displaystyle \frac{1}{4π^2 \: m}=0\text{,}225±0\text{,}02 \:\mathrm{kg^{-1}} .

dynOscLibres_corTP_Im/raideur.png

Caractéristiques du mouvement

• Le mouvement d'oscillation est amorti par des frottements visqueux (principalement sur l'électrode de mesure dans l'eau) et des frottements solides (principalement sur le banc, dont le coussin d'air n'est pas parfait, mais éventuellement aussi à cause de certains fils électriques de connexion des parties mobiles).

Bien que l'électrode mobile de mesure cause quelques turbulences locales dans l'eau, les frottements fluides turbulents sont normalement négligeables aux vitesses modérées étudiées.

• Les modélisations avec frottement solide seul et/ou frottement fluide seul peuvent se généraliser pour considére la somme des deux effets.

Dans le cas (par exemple) du banc horizontal, en notant  k=k1+k2k=k_1+k_2  la raideur de l'oscillateur, avec un frottement fluide visqueux (de constante λλ ) et un frottement solide (de norme ff ), l'équation différentielle est de la forme :  ẍ+2αx˙+ω02x=−εfm\displaystyle \ddot{x}+2 \,α \:\dot{x}+ω_0^{\:2} \: x=-\frac{ε \:f}{m}   avec   α=λ2m\displaystyle α=\frac{λ}{2 \,m}  ;  ω0=km\displaystyle ω_0=\sqrt{\frac{k}{m}}  ;  ε=sgn(x˙)ε=\mathrm{sgn}(\dot{x}) .

• Lors d'une demi oscillation partant de  x0>fk>0\displaystyle x_0>\frac{f}{k}>0  avec une vitesse initiale nulle, on obtient la solution :  x=fk+e−αt(x0−fk)[cos(ωt)−αωsin(ωt)]\displaystyle x=\frac{f}{k}+\mathrm{e}^{-αt} \; \left(x_0-\frac{f}{k}\right) \; \left[\cos(ω \,t)-\frac{α}{ω} \: \sin(ω \,t) \right]  avec une pulsation  ω=ω02−α2ω=\sqrt{ω_0^{\:2}-α^2}  (non modifiée par le frottement solide puisque ce dernier décale seulement d'une constante).

L'amplitude au début de la seconde demi oscillation est donc :  |x1|=(x0−fk)e−αT/2−fk\displaystyle | \,x_1 |=\left(x_0-\frac{f}{k}\right) \; \mathrm{e}^{-αT/2}-\frac{f}{k}  (et ainsi de suite pour les oscillations successives).

◊ remarque : l'intervalle d'arrêt limité par  ±fk\displaystyle ±\frac{f}{k}  n'est pas modifié par le frottement fluide puisque ce dernier est nul à l'arrêt.

• Ces expressions sont toutefois inutilement compliquées, car le frottement fluide est proportionnel à la vitesse donc prédomine nettement au début des oscillations ; inversement, c'est le frottement solide qui est prépondérant une fois que ces dernières ont été très amorties.

Pour confirmer ces modèles, on peut donc raisonnablement se limiter à modéliser séparément le début et la fin des oscillations (avec un exemple dont l'amortissement est non négligeable).

Étude expérimentale de l'amortissement

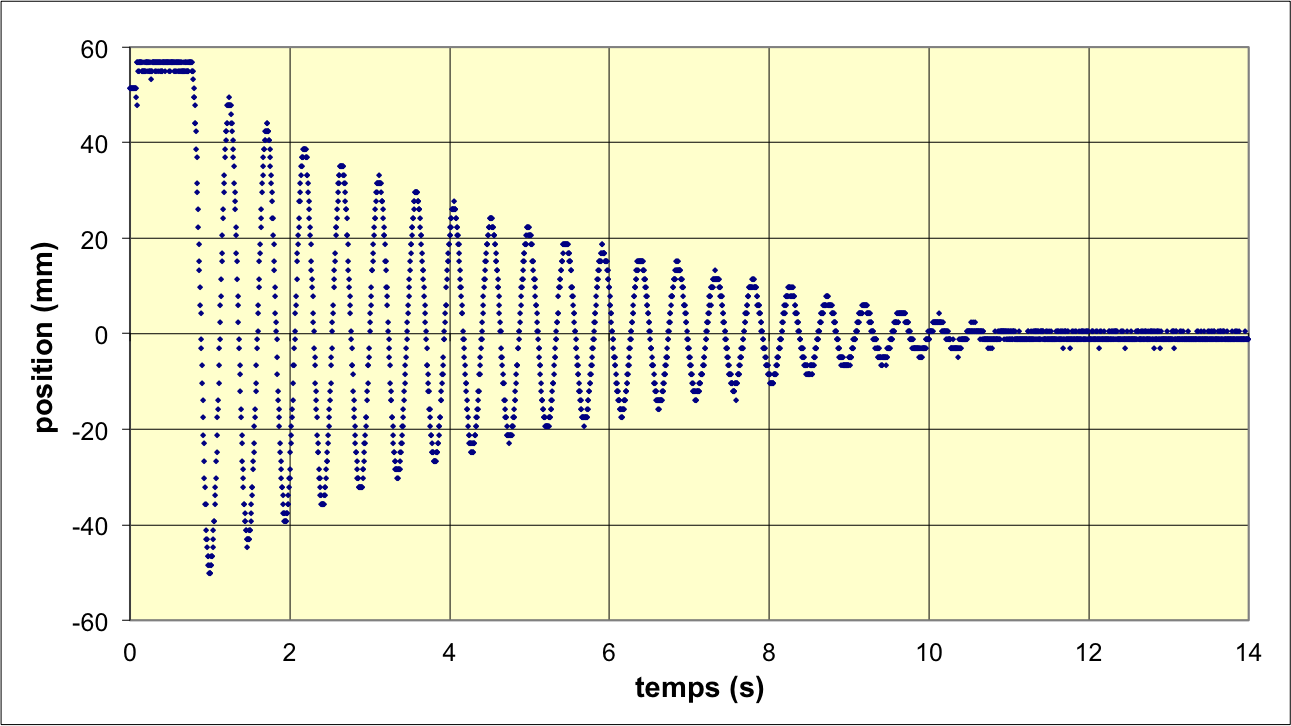
• Le mouvement peut être engistré avec un oscilloscope à mémoire, par l'intermédiaire du potentiel de l'électrode mobile.

dynOscLibres_corTP_Im/amortisement.png

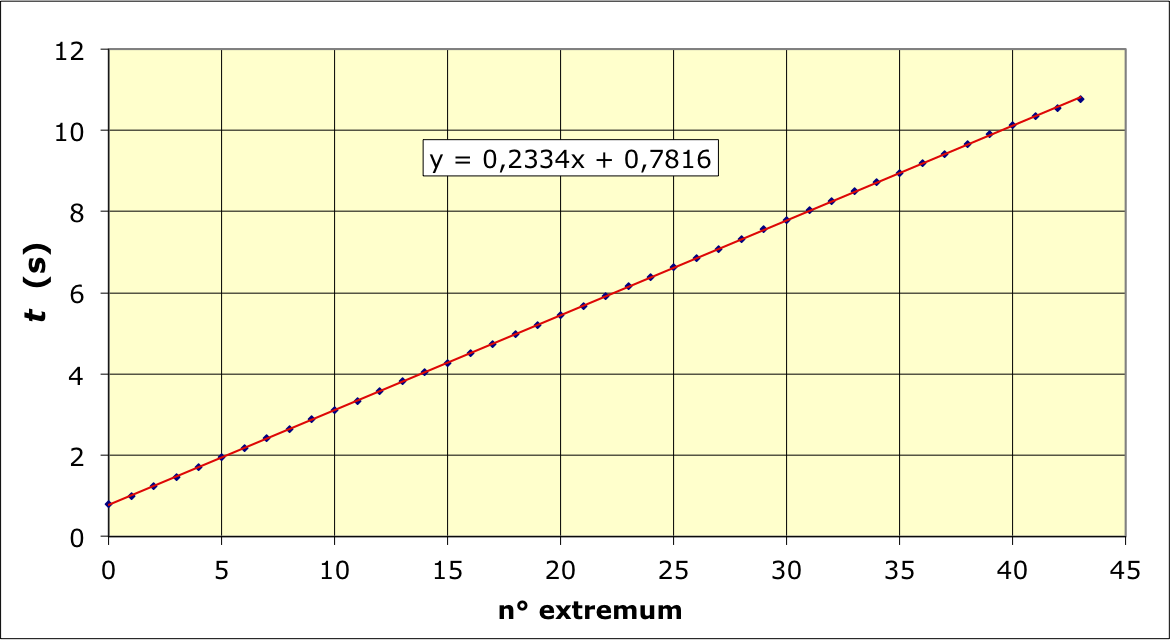
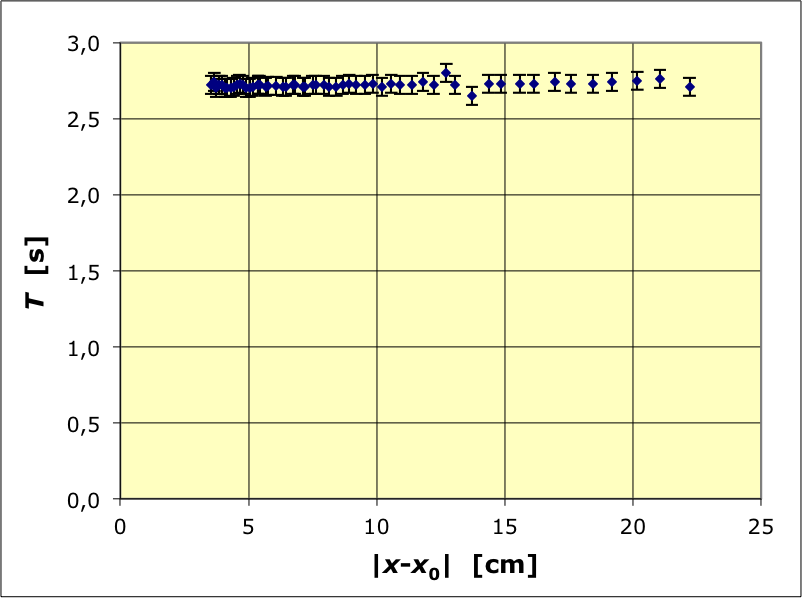
• Une première approche peut consister à tester la pseudo-période en comparant les instants des extremums successifs

On constate une évolution affine, caractéristique d'une pseudo-période constante  T= 0,467±0,002 s T=0\text{,}467±0\text{,}002 \:\mathrm{s} .

Pour cet exemple, la période propre est  T0=2πmk=0,476±0,006s\displaystyle T_0=2π \:\sqrt{\frac{m}{k}}=0\text{,}476±0\text{,}006 \:\mathrm{s}  ;  l'écart entre les deux valeurs est trop faible pour pouvoir en déduire α d'après l'expression théorique du modèle (les deux valeurs sont compatibles d'après les incertitudes).

dynOscLibres_corTP_Im/periode.png

• Pour l'étude directe de l'amortissement expérimental précédent, on est tenté à première vue d'interpréter avec une décroissance de type exponentiel ; une observation plus attentive suggère toutefois que l'atténuation finale est pour celà un peu “brusque”.

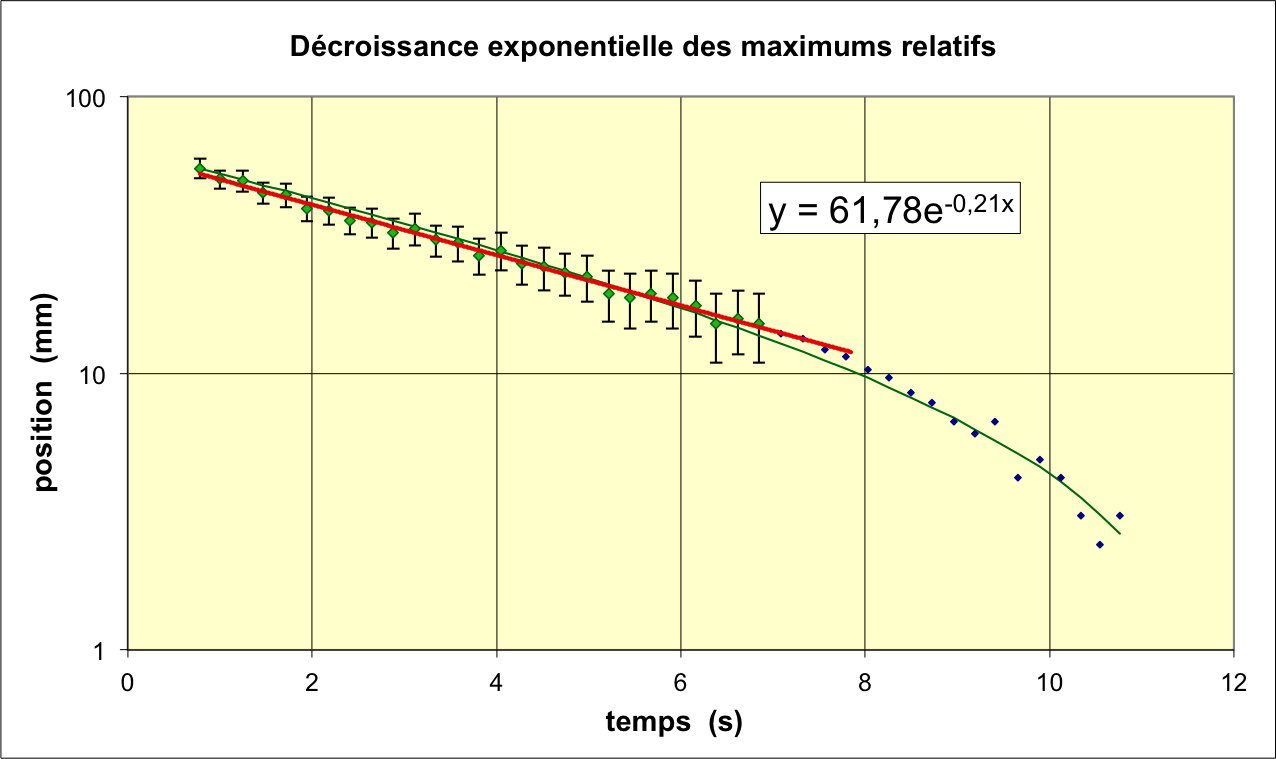
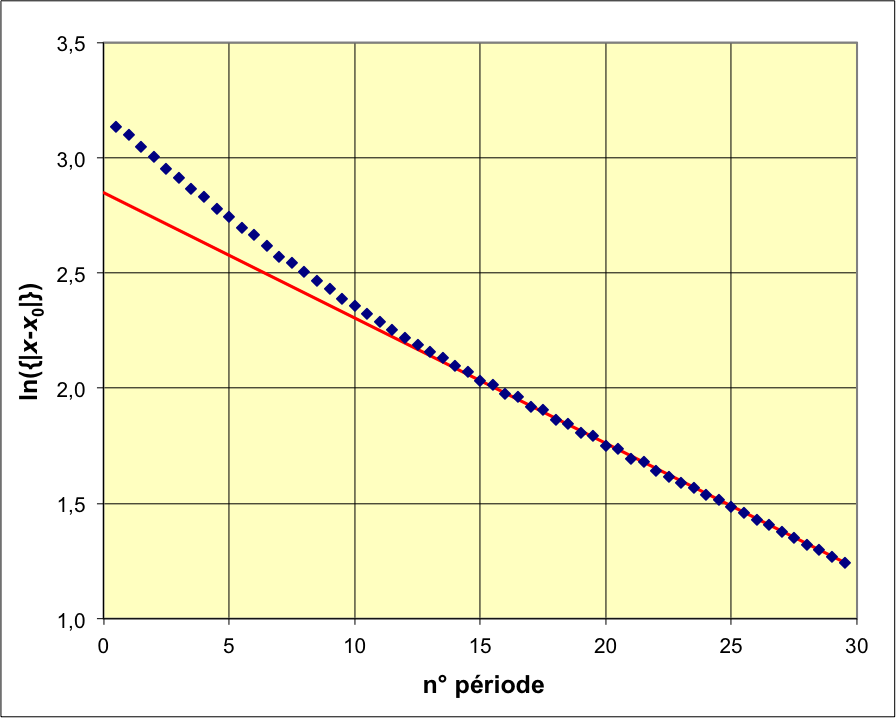
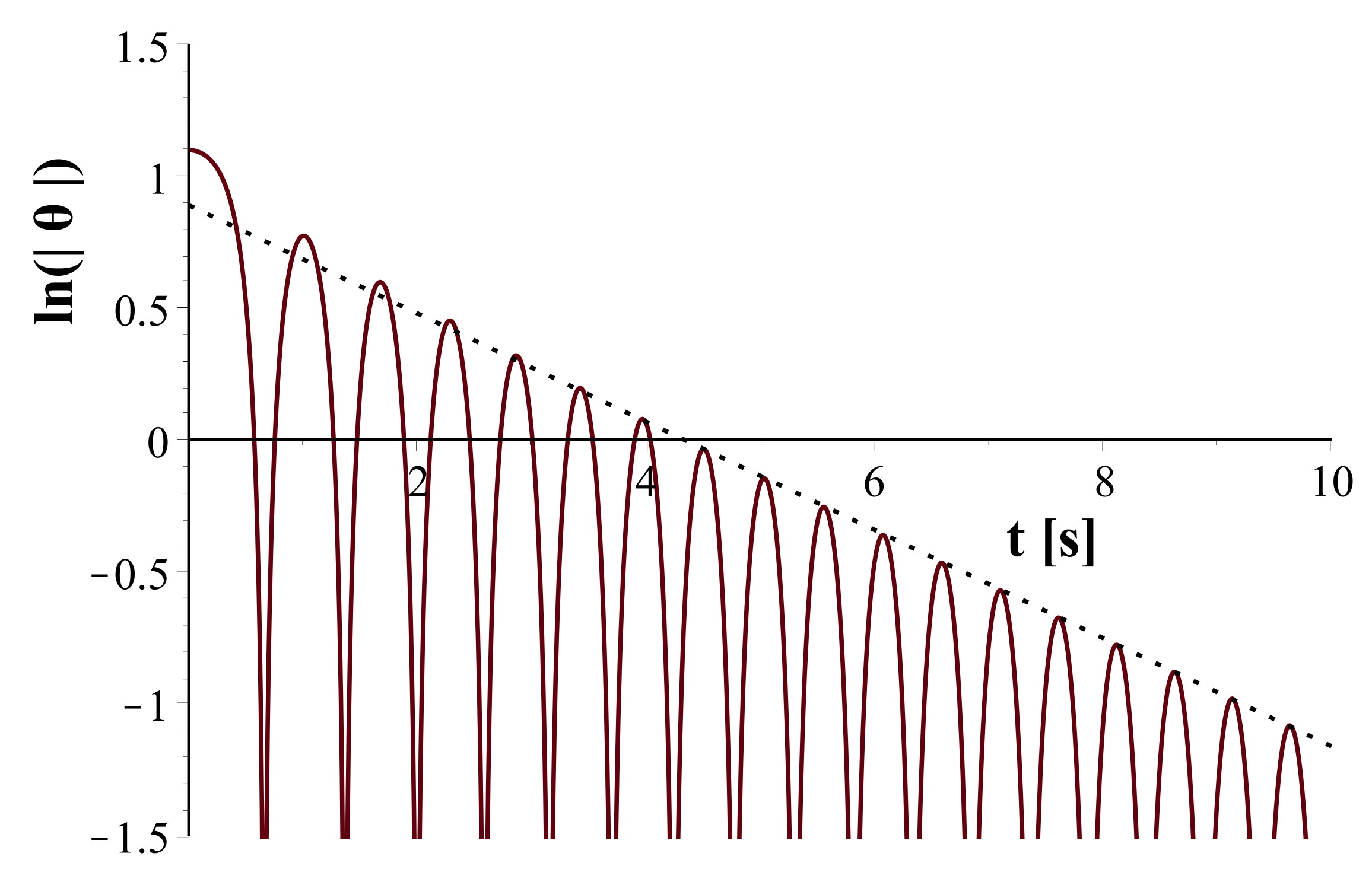
• La représentation graphique de la succession des extremums relatifs, en échelle logarithmique, montre que tout le début de la courbe est bien modélisé par une décroissance exponentielle ; la fin est par contre effectivement incompatible.

dynOscLibres_corTP_Im/exponentielle.png

On obtient ainsi  α=0,21±0,01s−1α=0\text{,}21±0\text{,}01 \:\mathrm{s^{-1}}  ; cela est effectivement très inférieur à  ω0=2πT0≈13,2rad.s−1\displaystyle ω_0=\frac{2π}{T_0} ≈13\text{,}2 \:\mathrm{rad.s^{-1}}  (c'est ce qui permet d'observer une vingtaine de pseudo-périodes).

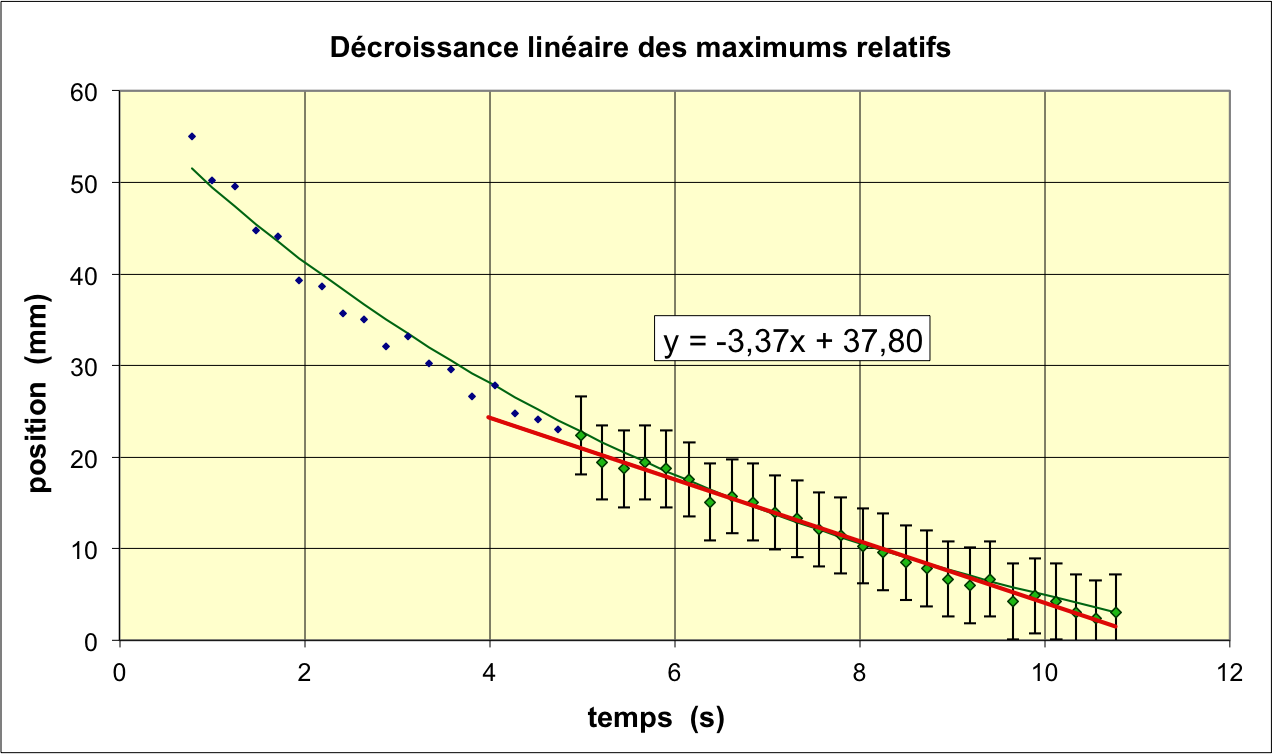
• Pour la fin de l'amortissement au contraire, une représentation en échelle linéaire est adaptée ; elle montre que la modélisation par un frottement solide est tout à fait satisfaisante.

On obtient un coefficient de décroissance  β=4fkT=3,37±0,20mm.s−1\displaystyle β=\frac{4 \:f}{k \:T}=3\text{,}37±0\text{,}20 \:\mathrm{mm.s^{-1}}  correspondant à  f=6,6±0,4mNf=6\text{,}6±0\text{,}4 \:\mathrm{mN} .

◊ remarque : à titre de comparaison, pour une amplitude d'oscillation XmX_m le frottement visqueux passe par des maximums  Fm=λωXm=4πmαTXm\displaystyle F_m=λ \:ω \:X_m=\frac{4π \:m \:α}{T} \: X_m  ;  avec ici  m= 96,3±2,0 g m=96\text{,}3±2\text{,}0 \:\mathrm{g}  cela donne au début  Fm≈27mNF_m≈27 \:\mathrm{mN}  ; bien que cela soit un maximum et non une moyenne, il faut que l'amplitude soit divisée par trois pour que le frottement solide devienne prépondérant.

dynOscLibres_corTP_Im/affine.png

◊ remarque : la méthode consistant à simplifier les calculs en séparant le domaine d'étude en zones de prépondérance est assez générale et utile dans de nombreuses parties des sciences physiques.

Énergie mécanique

• On étudie un cas d'oscillateur sur banc à coussin d'air avec frottement visqueux (très faible). La masse du palet mobile est  m= 197,6±0,4 g m=197\text{,}6±0\text{,}4 \:\mathrm{g}  mais on se demande s'il ne faut pas prendre en compte une partie de la masse des ressorts (participant forcément au mouvement).

Puisque dans ce cas  T≈T0T≈T_0  en excellente approximation, on mesure alors  30 T= 15,6±0,2 s 30 \:T=15\text{,}6±0\text{,}2 \:\mathrm{s}  et la raideur  k=29,2±0,2N.m−1k=29\text{,}2±0\text{,}2 \:\mathrm{N.m^{-1}}  ;  on en déduit une masse oscillante  m= 200±7 g m=200±7 \:\mathrm{g}  tout à fait compatible, montrant que la contribution des ressorts à la masse est de toute façon inférieure aux incertitudes.

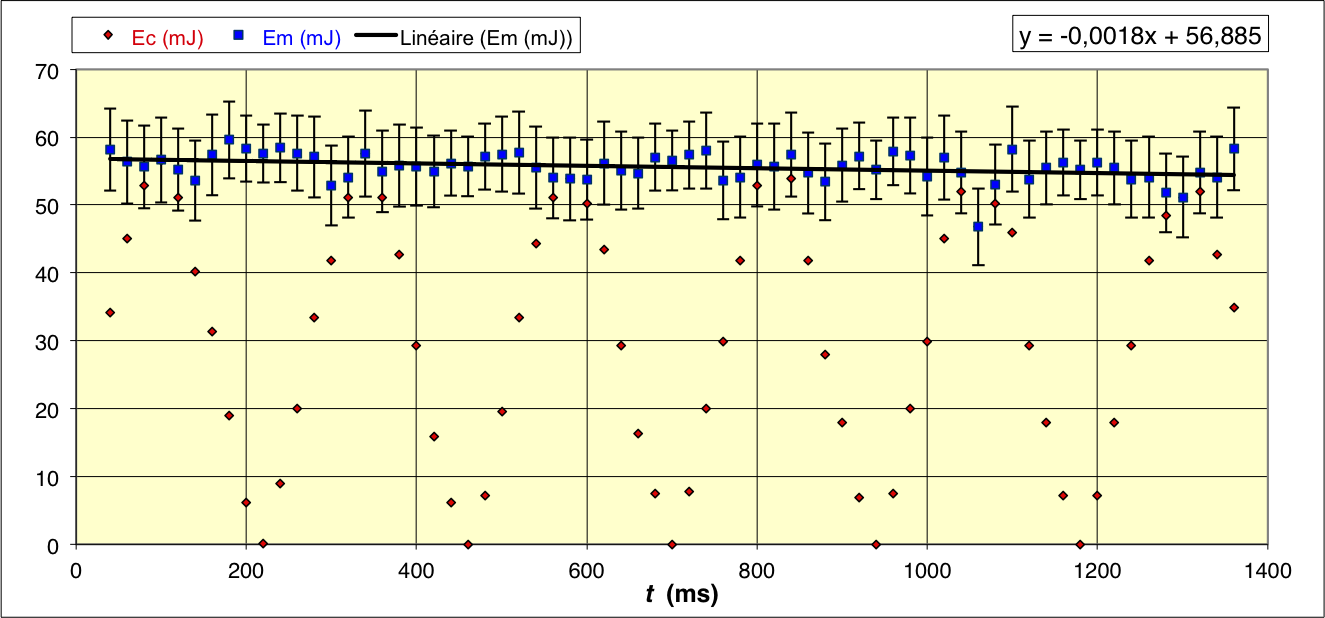
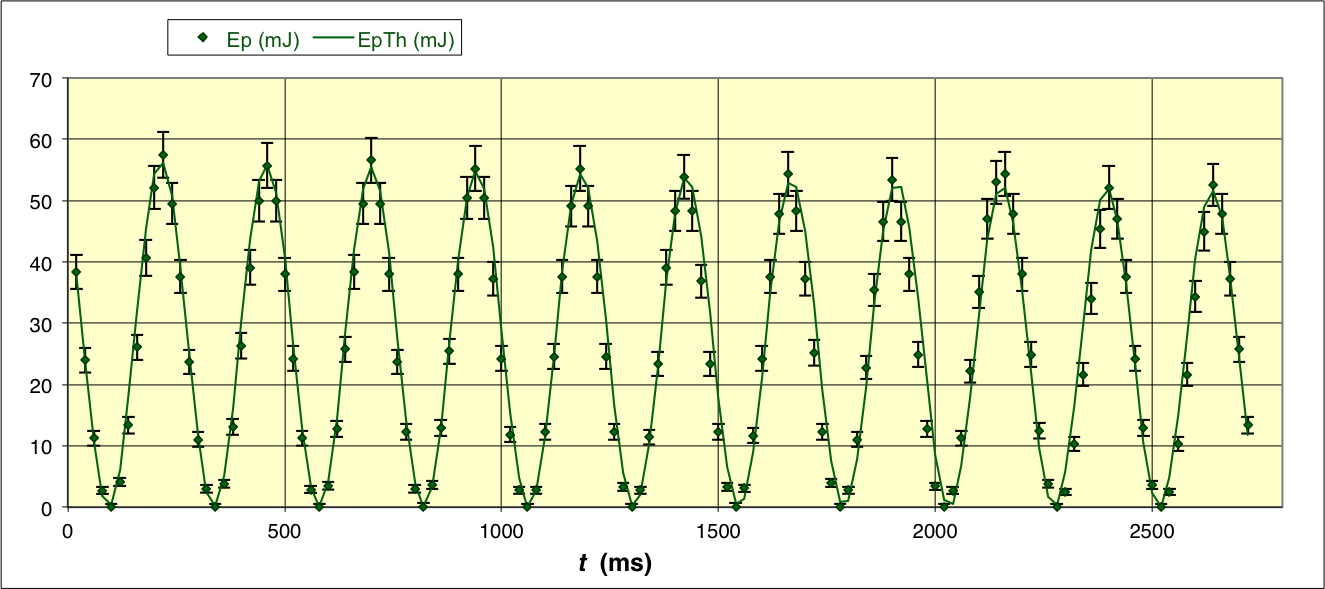
• En utilisant le modèle associé  x=Xm e−αt cos (ω t +ϕ) x=X_m \; \mathrm{e}^{-αt} \; \cos(ω \,t+ϕ)  on décrit l'énergie potentielle  Ep=12kx2E_p=\frac{1}{2} k \:x^2  et l'énergie cinétique  Ec=12mx˙2E_c=\frac{1}{2} m \:\dot{x}^2  ainsi que l'énergie mécanique correspondante.

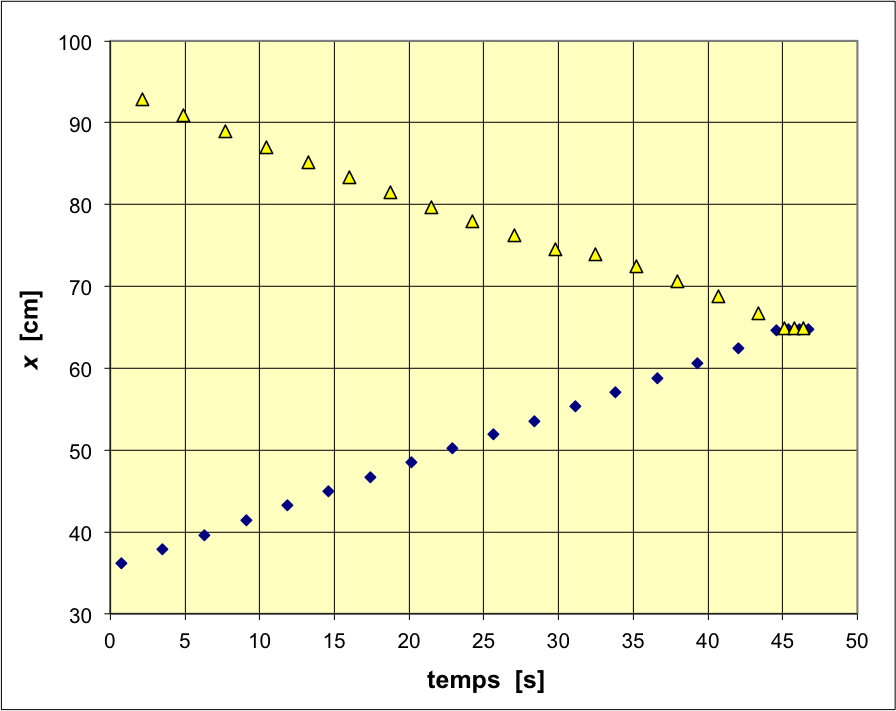
On peut alors ajuster les paramètres du modèle pour décrire au mieux les mesures.

dynOscLibres_corTP_Im/EcEm.png


dynOscLibres_corTP_Im/Ep.png

On constate que la modélisation est satisfaisante sur le détail de cinq périodes ; l'amortissement est en fait assez faible pour qu'une approximation affine de l'exponentielle soit suffisante.

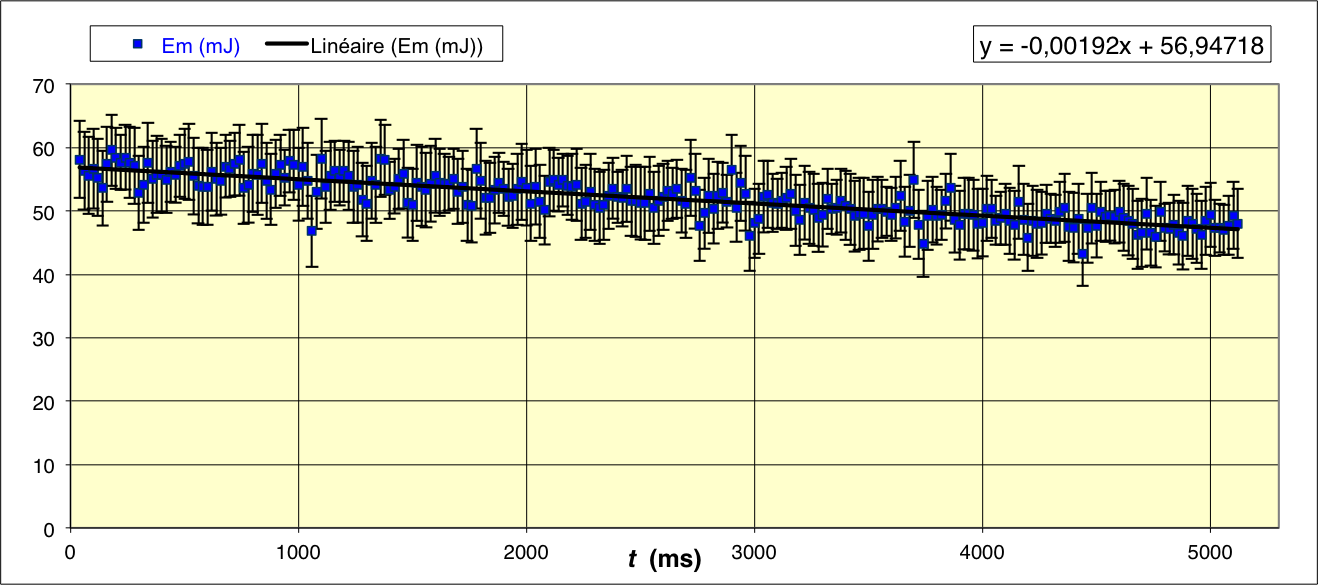
dynOscLibres_corTP_Im/Em.png

L'étude de la décroissance de EmE_m sur l'ensemble des cinq secondes mesurées confirme la conclusion précédente ; on obtient ainsi  α=1,92±0,02s−1α=1\text{,}92±0\text{,}02 \:\mathrm{s^{-1}} .

◊ remarque : cet amortissement est plus important que celui de l'exemple précédent ; il aurait pu être intéressant de mesurer sur une plus grande durée pour constater le caractère exponentiel, mais le dispositif d'enregistrement utilisé (dans les années 1995...) imposait un compromis entre la durée d'ensemble et le détail des variations sur chaque période.

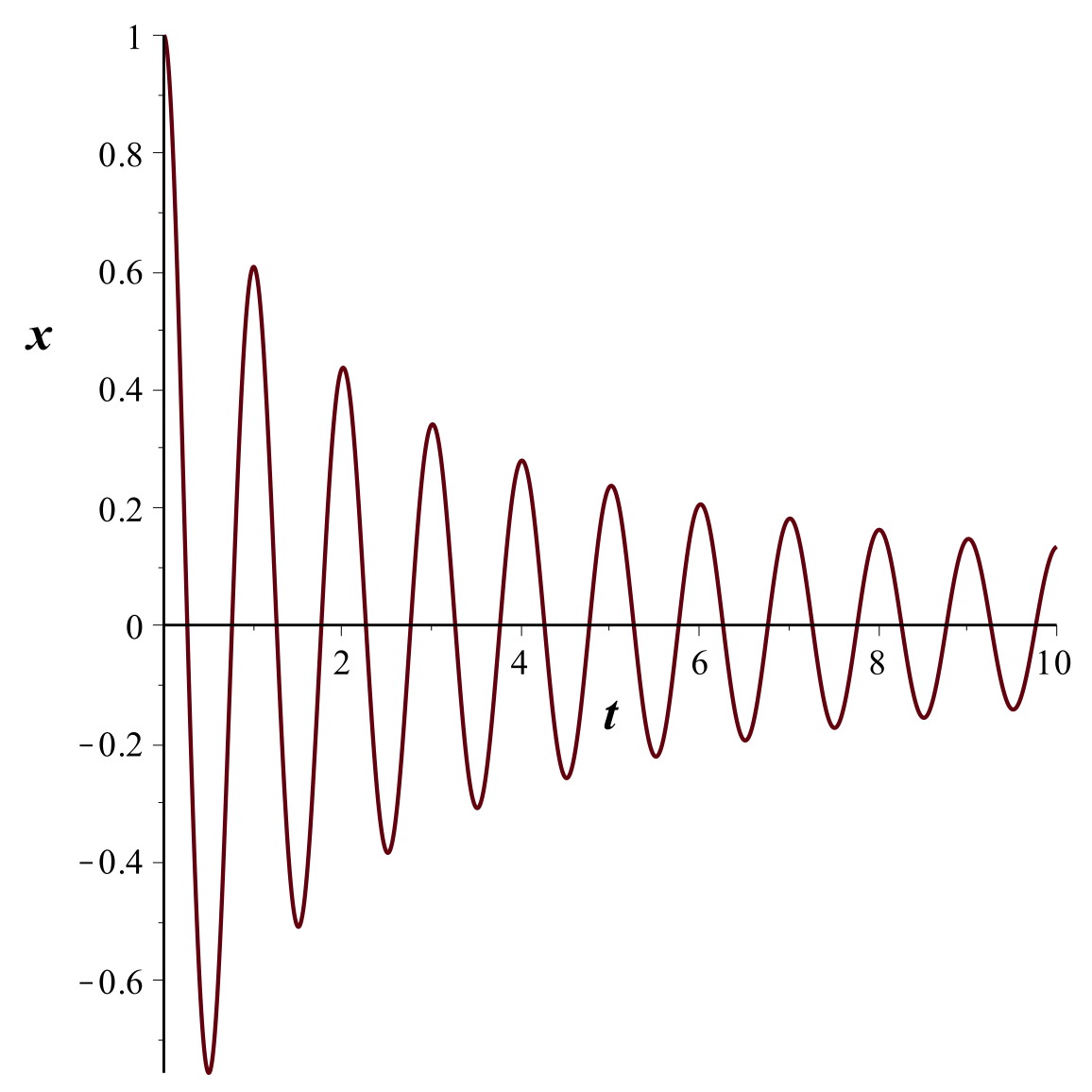
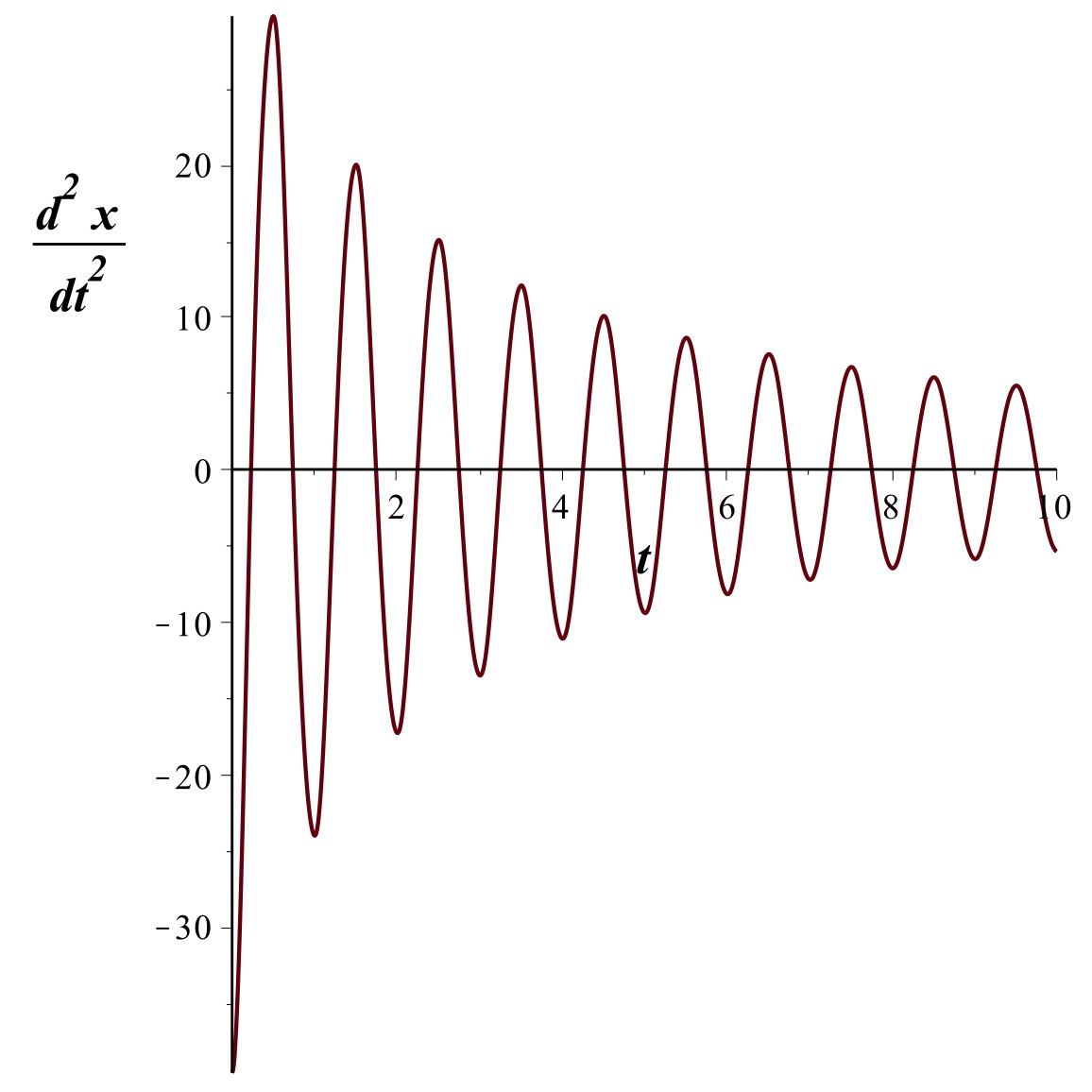
Amortissement turbulent

• Quelques essais ont été tentés, en fixant une petite “palette” de carton sur l'électrode de mesure afin d'augmenter les turbulences ; hélas sans aboutir à des données expérimentales convaincantes. Pour montrer tout de même une méthode possible, on choisit ici de générer informatiquement une série de points par intégration numérique de l'équation.

On constate au début un amortissement plus rapide que pour un frottement visqueux (turbulences plus importantes quand la vitesse est plus grande).

dynOscLibres_corTP_Im/turbulent_1.jpg

• Pour tester une modélisation de frottement en v2v^2 (ou plus généralement en vkv^k ), on ne peut pas trouver de solution littérale théorique car l'équation différentielle est non-linéaire.

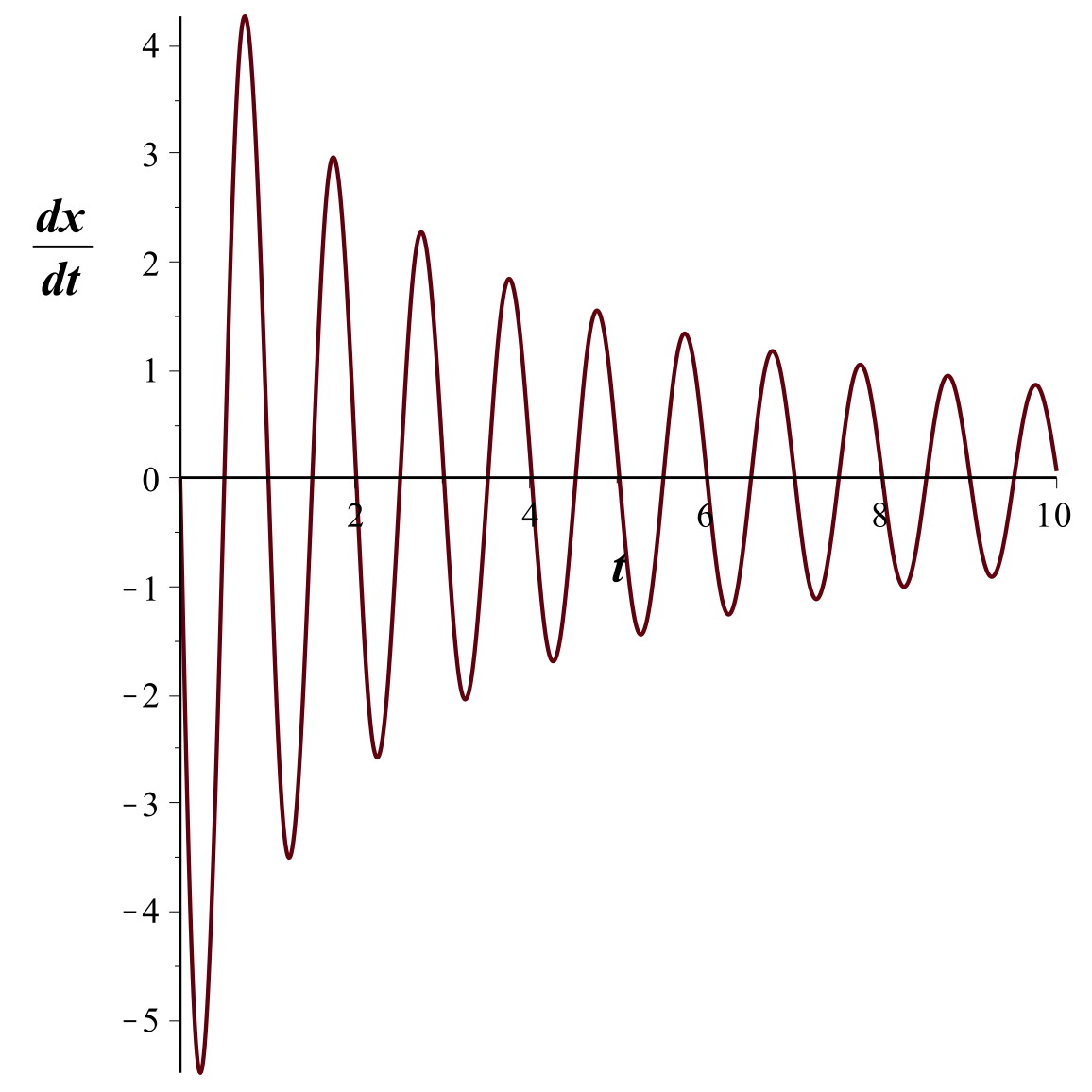
On peut par contre, pour chaque point mesuré  x(t)x(t) , ajuster un polynôme (de degré 3 ou 4 ) sur un groupe avec trois points avant et trois après ; en dérivant ce dernier, on en déduit des estimations locales de la dérivée x˙(t)\dot{x}(t) et de la dérivée seconde ẍ(t)\ddot{x}(t) .

◊ remarque : cela nécessite au moins ≈50≈50 points par période (pour la précision des ajustements).

dynOscLibres_corTP_Im/turbulent_2.jpg
dynOscLibres_corTP_Im/turbulent_3.jpg

• On peut ensuite les reporter dans l'équation différentielle et ajuster globalement les coefficients du modèle pour que celle-ci soit vérifiée au mieux.

Une méthode simple consiste toutefois à commencer par calculer TT et ωω d'après les points calculés (pour tester la méthode il faut procéder “comme si” il s'agissait de points mesurés). Les passages par  x=0x=0  donnent  9,5T=9,7659\text{,}5 \:T=9\text{,}765 (ici unités arbitraires) d'où  ω=6,282ω=6\text{,}282 (unités arbitraires) tout à fait compatible avec la valeur  ω0=6,283ω_0=6\text{,}283  utilisée dans la génération des points (l'amortissement a donc dans ce cas une influence négligeable).

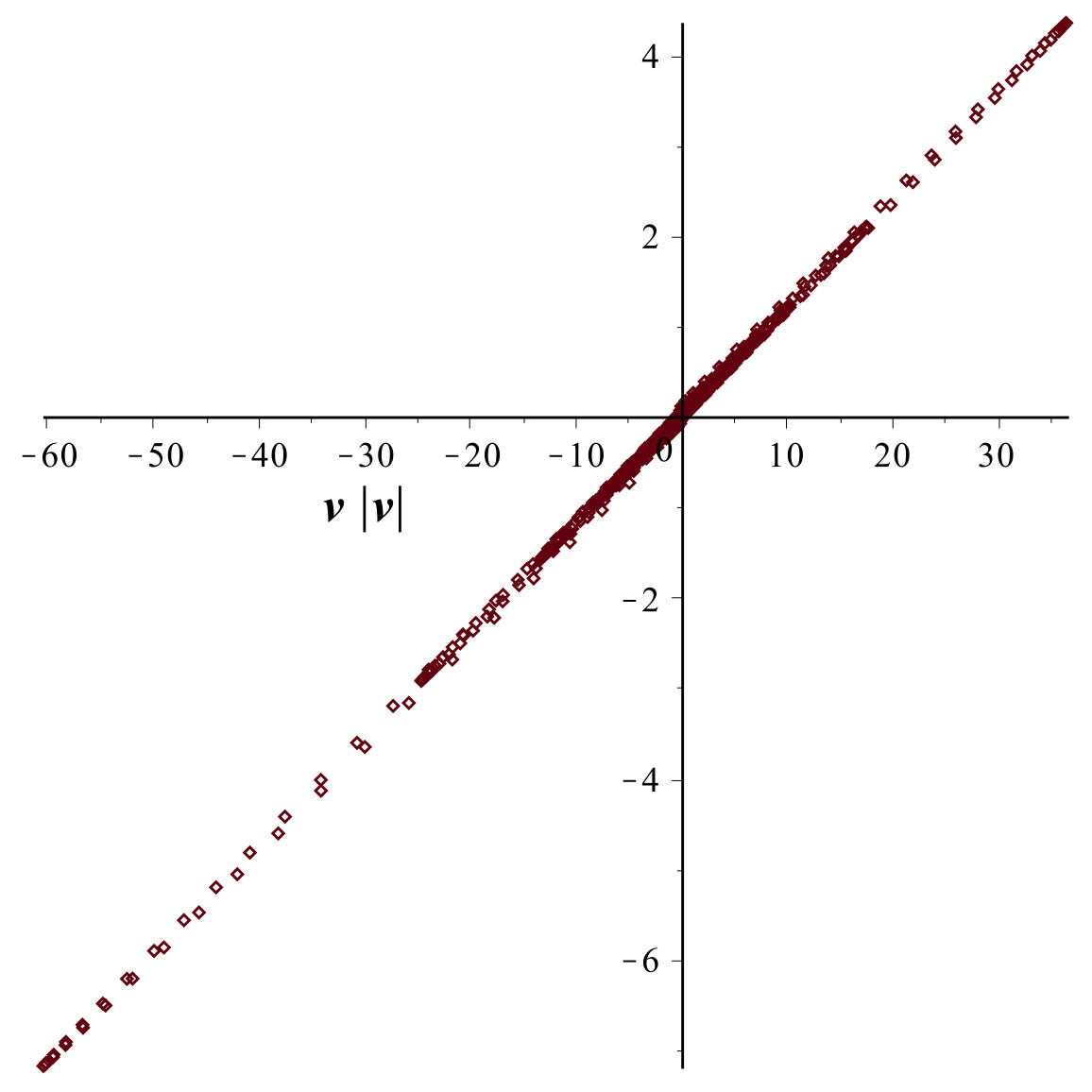
• On peut en déduire  −ẍ−ω2x-\ddot{x}-ω^2 \: x  afin de comparer au terme de frottement présupposé  βx˙|x˙|β \:\dot{x} \: |\dot{x} \:| .

dynOscLibres_corTP_Im/turbulent_4.jpg

Le fait d'obtenir une proportionnalité confirme l'expression proposée pour le frottement ; l'ajustement d'une droite passant par l'origine donne un coefficient  β=0,119β=0\text{,}119 (unités arbitraires) tout à fait en accord avec la valeur  β=0,12β=0\text{,}12  utilisée pour la génération des points.

◊ remarque : si on obtient une courbe régulière mais non linéaire, on peut tester une expression en vkv^k avec un diagramme logarithmique.


Pendule pesant

Grandes oscillations

• Le moment du poids peut s'écrire  ℳ=Mg𝓁ℳ=M \:g \:𝓁  en notant MM la masse, 𝓁𝓁 la distance entre le centre d'inertie et l'axe de rotation, θθ l'angle par rapport à la verticale.

L'étude du moment d'intertie du pendule en fonction de la répartition des masses n'a pas été envisagée ici. Étant donné que le pendule est principalement constitué d'une masse MM (de dimension modérée en comparaison de sa taille) fixée sur une tige (de masse faible en comparaison) à une longueur  ≈𝓁≈𝓁  de l'axe de rotation, on peut noter  I≈M𝓁2I≈M\: 𝓁^2  le moment d'inertie.

En négligeant les l'amortissement en première approximation, l'équation différentielle est ainsi de la forme :  θ̈+ω02sin(θ)=0\ddot{θ}+ω_0^{\:2} \; \sin(θ)=0   avec  ω0=ℳ𝓁≈g𝓁\displaystyle ω_0=\sqrt{\frac{ℳ}{𝓁}}≈\sqrt{\frac{g}{𝓁}} .  On ne cherchera pas à préciser ici.

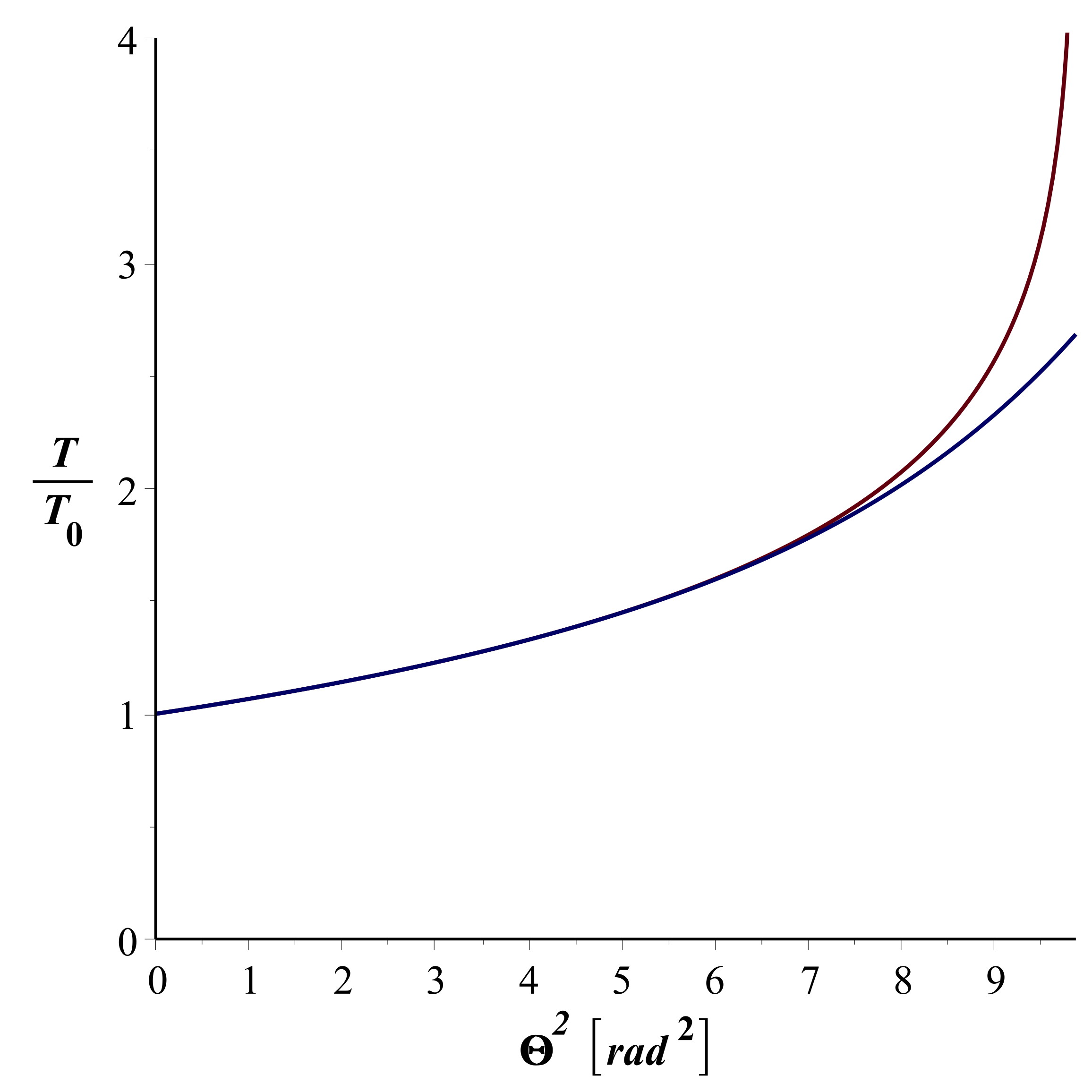
• Dans la limite des petites oscillations  sin(θ)≈θ\sin(θ)≈θ  donne la solution  θ(t)≈Θcos(ω0t)θ(t)≈Θ \; \cos(ω_0 \, t)  pour un départ immobile à la position ΘΘ .

• Pour les grandes oscillations, une première intégration donne :  θ˙=2ω0cos(θ)−cos(Θ)\dot{θ}=\sqrt{2} \; ω_0 \: \sqrt{\cos(θ)-\cos(Θ)} .  Par séparation des variables, on obtient ainsi :  T=4∫0T/4dt=22ω0∫0Θdθcos(θ)−cos(Θ)\displaystyle T=4 \:∫_0^{T/4} dt=\frac{2 \;\sqrt{2}}{ω_0} \, ∫_0^Θ \frac{dθ}{\sqrt{\cos(θ)-\cos(Θ)}} .

On peut intégrer numériquement ou utiliser un développement limité, mais avec un logiciel de calcul formel car un calcul à l'ordre 7 en Θ2Θ^2 (la fonction est paire) est nécessaire :
TT0≈1+116Θ2+113072Θ4+173737280Θ6+229311321205760Θ8⋯\displaystyle \frac{T}{T_0} ≈1+\frac{1}{16} \: Θ^2+\frac{11}{3072} \: Θ^4+\frac{173}{737280} \: Θ^6+\frac{22931}{1321205760} \: Θ^8 \:⋯
⋯+1319183951268147200Θ10+2335264632009078326886400Θ12+2673857519265928913086054400Θ14+⋯\displaystyle ⋯ +\frac{1319183}{951268147200} \: Θ^10+\frac{233526463}{2009078326886400} \: Θ^12+\frac{2673857519}{265928913086054400} \: Θ^14+ \:⋯

dynOscLibres_corTP_Im/pendPes.jpg

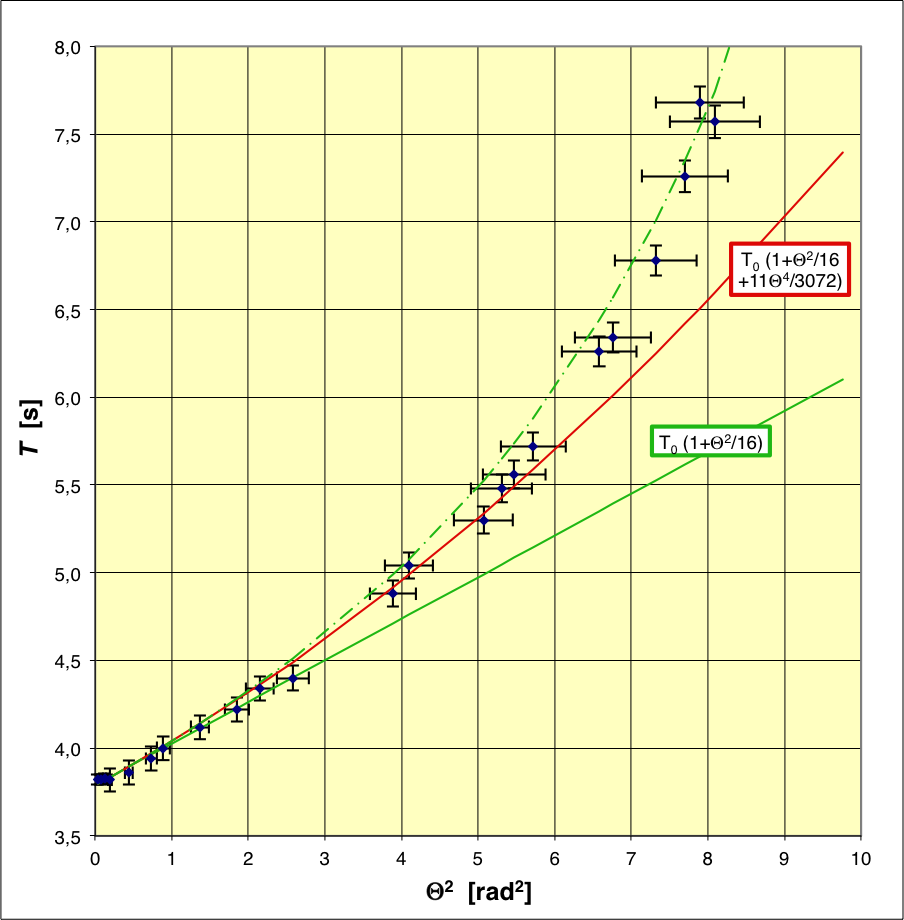
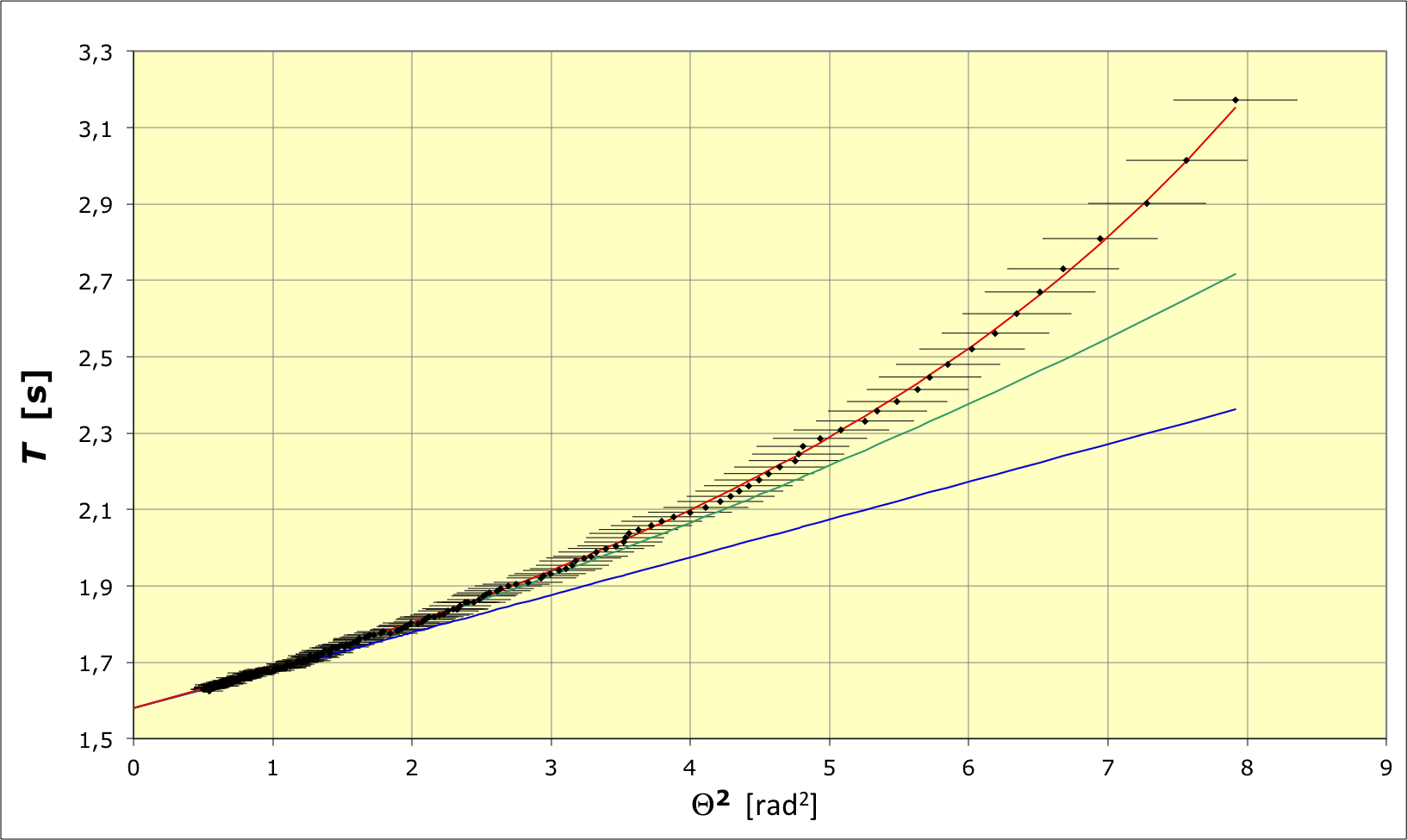
• Pour les mesures, une approche simple consiste à placer un écran derrière le pendule et à y projeter l'image d'un rapporteur (le rétro-projecteur est adapté).

On lâche le pendule initialement immobile à une amplitude Θ0Θ_0 ; on mesure une période et on repère la position Θ1Θ_1 de remontée (il y a un inévitable léger amortissement). Pour une meilleure précision, il est préférable de mesurer plusieurs fois et de calculer la moyenne. On utilise ensuite  Θ=Θ0+Θ12\displaystyle Θ=\frac{Θ_0+Θ_1}{2} .

dynOscLibres_corTP_Im/pendPes-1.png

Les mesures sont bien modélisées par le développement limité à l'ordre 7 en Θ2Θ^2 . Le développement à l'ordre 1 en Θ2Θ^2 est toutefois correct jusqu'à  Θ≈π2Θ≈\frac{π}{2} ; celui à l'ordre 2 en Θ2Θ^2 est correct jusqu'à  Θ≈3π4Θ≈\frac{3 \,π}{4} .

• Une approche plus élaborée a été possible lorsqu'on a trouvé un modèle de résistance réglable par un bouton tournant, avec un très faible frottement. En fixant la résistance sur le pendule et en bloquant le bouton avec un support, on peut inclure la résistance dans un circuit électrique avec pont diviseur de tension et mesurer ainsi un grand nombre d'oscillations avec un grand nombre de points.

À l'aide du dispositif avec rapporteur, on étalonne le circuit de mesure.

dynOscLibres_corTP_Im/pend_200s_etal.png

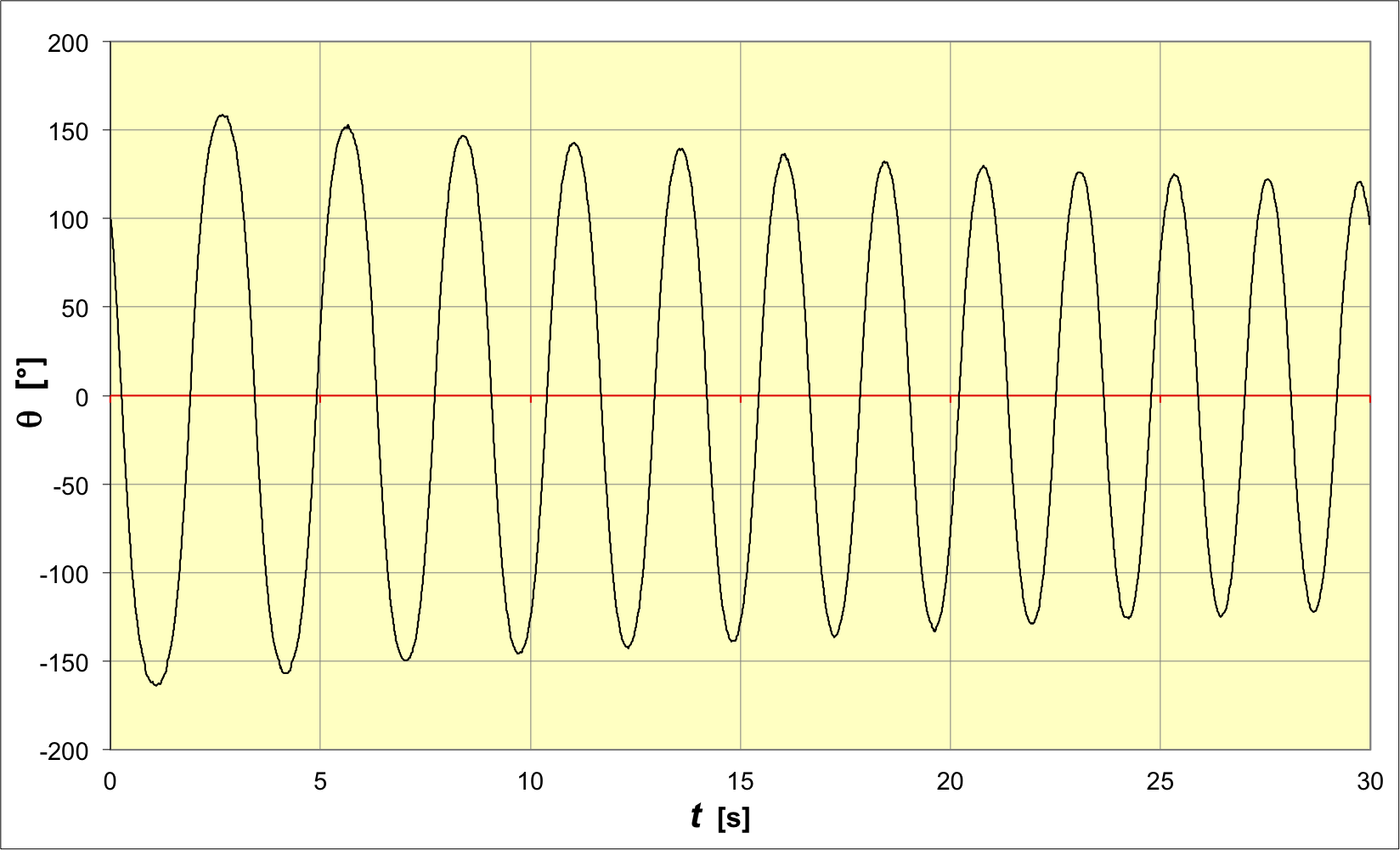
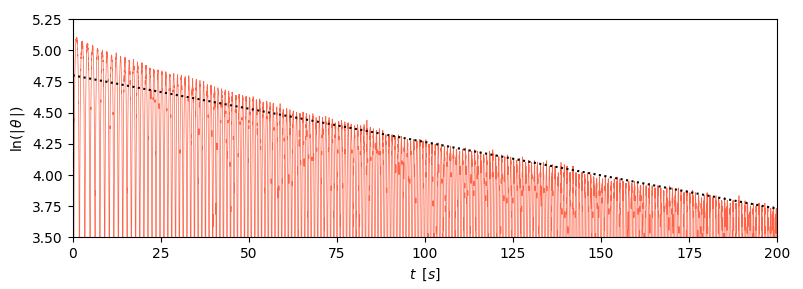
Avec un oscilloscope à mémoire, on enregistre ensuite 50000 points sur  200s200 \:\mathrm{s} . Les mesures étant très rapprochées, on peut ainsi éliminer la plupart des parasites en lissant sur 7 points (3 avant ; 3 après). On obtient une courbe d'évolution sur plus de 120 périodes.

dynOscLibres_corTP_Im/pend_200s_osc.png

• Pour chaque (pseudo)-période on calcule la durée et l'amplitude ; ceci donne un graphique analogue à celui obtenu par la méthode simple, mais plus complet ; les conclusions sont les mêmes.

dynOscLibres_corTP_Im/pend_200s_T.png

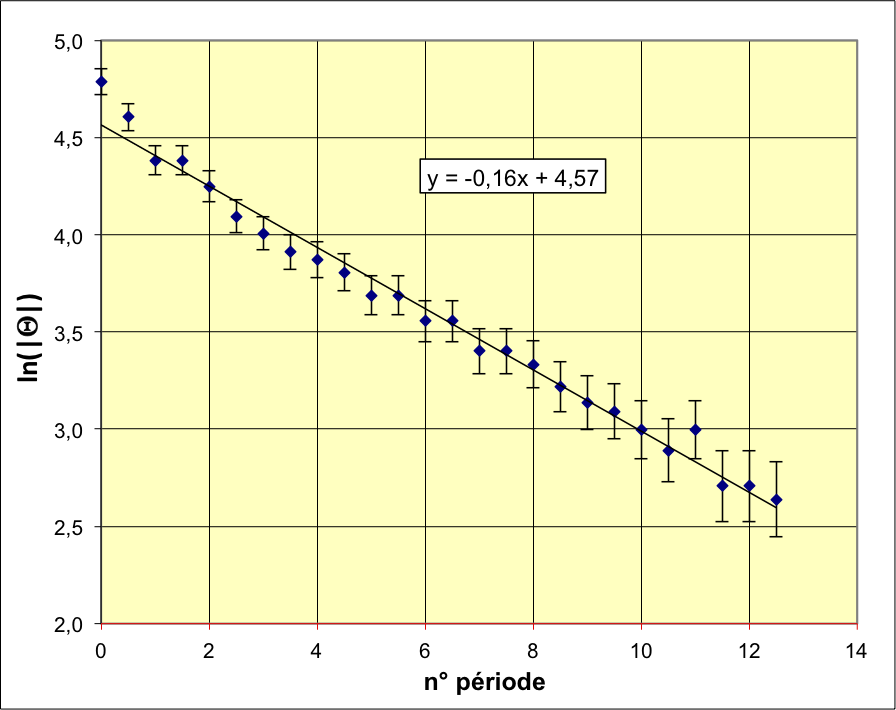
Amortissement

• Pour étudier l'amortissement des oscillations, on peut utiliser la méthode simple déjà évoquée, consistant à repérer les maximums successifs avec une projection d'un rapporteur (les étudiants n'ont pas mesuré la période).

dynOscLibres_corTP_Im/amort_fluide.png

La décroissance affine du logarithme de l'amplitude justifie une modélisation par un amortissement fluide visqueux, à part peut-être tout au début.

Faute d'informations plus précises sur le mouvement, on ne peut pas savoir si cela est dû au fait que les vitesses sont plus grandes au début, d'où une contribution possible de frottement turbulent, ou bien au fait que pour les grandes amplitudes les caractéristiques du mouvement diffèrent de celles du pendule élastique.

• Un autre groupe a utilisé un dispositif à capteur infrarouge pour mesurer le déplacement horizontal de l'extrémité du pendule, mais ils n'ont pas mesuré avec précision la position du réflecteur ( L≈50cmL≈50 \:\mathrm{cm} ). Or, cela intervient pour calculer l'amplitude angulaire ; heureusement, la disposition du faisceau limite aussi l'amplitude (maximum ≈27°≈27° ) donc l'approximation  ∆xL=sin(θ)≈θ\displaystyle \frac{∆x}{L}=\sin(θ)≈θ  est raisonnable (écart ≲1%≲1% comparable aux incertitudes). Ils ont raisonné avec ∆x∆x .

Ils ont par contre mesuré la (pseudo)-période et vérifié que, dans ces conditions limitées, elle ne dépend pas de l'amplitude (l'éventuelle augmentation aux plus grandes amplitudes est comparable aux incertitudes).

dynOscLibres_corTP_Im/pseudoPer.png

• La décroissance du logarithme de l'amplitude n'est par contre pas compatible avec un frottement fluide visqueux. En pratique, les étudiants avaient augmenté le frottement sur l'air en fixant sur le pendule une plaquette de carton ; cela provoque des turbulences pour les plus grandes vitesses au début des mesures. Cet effet ne peut pas être étudié plus précisément car les étudiants n'ont pas conservé l'intégralité des mesures en fonction du temps.

dynOscLibres_corTP_Im/amort_turb.png

• Ce groupe a par contre aussi testé les oscillations avec un frottement solide : le support du pendule comporte un dispositif à vis permettant cela à l'aide d'un serrage à vis.

Pour des amplitudes relativement faibles ( ∆x≤30cm∆x≤30 \:\mathrm{cm} ) on vérifie la décroissance affine caractéristique du frottement solide comme pour un oscillateur à ressorts.

dynOscLibres_corTP_Im/AmortSol.png

• Pour ce qui concerne l'éventualité d'un frottement turbulent, on peut penser à utiliser les données enregistrées par le groupe qui a étudié les grandes amplitudes. On y voit effectivement une variation non affine du logarithme aux grandes amplitudes. Cet effet reste toutefois modéré car ce groupe ne recherchait pas à augmenter le frottement fluide, donc n'a pas ajouté de plaquette de carton sur l'axe du pendule.

dynOscLibres_corTP_Im/oscillAmPend.png

Or l'équation du pendule pesant n'est pas linéaire ; une simulation par intégration numérique montre que pour un frottement visqueux cela perturbe la variation affine du logarithme aux grandes amplitudes. L'éventuel effet turbulent n'est ainsi nulle part assez prépondérant pour être clairement étudié (ici, il n'y a pas besoin de beaucoup de périodes mais il faut plus de points par période).

dynOscLibres_corTP_Im/oscillAmPend.jpg


Autres initiatives à volonté

• Compte tenu des commentaires sur les différentes expériences abordées (de façon sous-jacente, on y devine l'évolution technique entre 1980 et 2020 - même si des résultats intéressants peuvent être obtenus avec du matériel très basique, en procédant ingénieusement) on peut reprendre certaines expériences afin d'en améliorer les résultats...

• On peut aussi s'intéresser à d'autres aspects, par exemple le pendule pesant composé, le pendule de torsion...