DYNAMIQUE - OSCILLATIONS LIBRES - exercices



A. EXERCICES DE BASE

Résonateur de Helmholtz

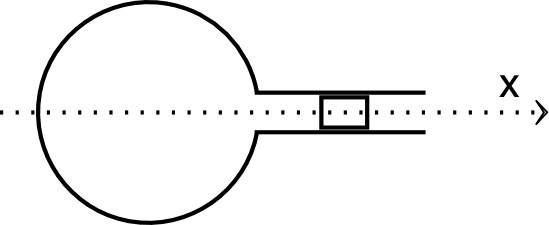
        • Un volume d'air  V0V_0  à la pression  p0p_0  (égale à la pression extérieure) est contenu dans un récipient dont le goulot tubulaire (de longueur  𝓁𝓁  et de section  ss ) est fermé par un piston. Ce dernier, de masse  mm , peut coulisser sans frottement dans la partie tubulaire ; on note  xx  son abscisse par rapport à la position d'équilibre prise comme origine. Lorsqu'on écarte le piston de sa position d'équilibre, il oscille.
dynOscLibres_ex_Im/dynOscLibres_ex_Im1.jpg

        • En admettant que le gaz dans le récipient évolue de façon adiabatique (sans transfert de chaleur), on peut montrer (en thermodynamique) que la pression évolue selon la loi :   pVγ=p0V0γp \:V^γ = p_0 \: V_0^{\:γ}   où  γγ  est un coefficient caractéristique des propriétés du gaz :  γ=1,4γ=1\text{,}4  pour l'air. En déduire la période des petites oscillations.
        • En considérant le même récipient mais sans piston, on peut faire osciller l'air contenu dans le goulot. En prenant pour masse  mm  la masse de l'air contenu dans le goulot, calculer la fréquence des oscillations.
        ◊ remarque : on ne tient pas compte ici des effets de propagation ; ceci suppose que la longueur d'onde  λλ  obtenue est telle que  λ3≫V0λ^3≫V_0 .


Oscillation au voisinage d'un équilibre

        • Un bol a la forme d'un paraboloïde de révolution d'axe (Oy)(Oy) vertical ; soit  y=ax2y=a \:x^2  l'équation de sa section méridienne. On lâche en un point de la surface intérieure, avec une vitesse initiale nulle, un point matériel pouvant glisser sans frottement sur la surface du bol. Montrer que le mouvement est périodique. Exprimer la période dans le cas particulier des petites oscillations.


Oscillateur anharmonique et dilatation

       • Un point matériel MM , de masse mm , est mobile sur un axe OxOx ; son énergie potentielle peut s’écrire sous la forme :   Ep=12kx2−13ksx3E_p=\frac{1}{2} k \:x^2-\frac{1}{3} k \:s \:x^3   où  kk  et  ss  sont des constantes positives.

1.     • Tracer la courbe représentant  Ep=Ep(x)E_p=E_p (x)  et montrer que seule la position  x=0x=0  correspond à un équilibre stable.

2.     • On étudie le mouvement de MM au voisinage de  x=0x=0  ;  montrer que ceci correspond à  x≪1s\displaystyle x≪\frac{1}{s} .  Écrire dans ces conditions l'équation du mouvement.

3.     • On cherche une solution de la forme :   x=A.[cos(ω0t)+εf(t)]x=A .\left[\cos(ω_0 \, t)+ε \:f(t)\right]   où  ω0=km\displaystyle ω_0=\sqrt{\frac{k}{m}} ,  où f(t)f(t) est une fonction inconnue de  t t   et où   A≪1s\displaystyle A≪\frac{1}{s}   et   ε≪1ε≪1   sont des constantes. Interpréter cette expression de xx .
        • Après substitution dans l'équation du mouvement, montrer que :  f(t)≈cos(2ω0t)+af(t)≈\cos(2 \,ω_0 \, t)+a   et expliciter les constantes  εε  et  aa  en fonction de  ss  et  AA .

4.     • Calculer la valeur moyenne de  xx  au cours du temps (ceci correspond à la position moyenne au voisinage de l'équilibre).
        • On suppose que ce calcul correspond au mouvement de l'un des atomes d'un cristal, dans une direction, au voisinage de sa position d'équilibre. En considérant que l'énergie moyenne de l'énergie d'agitation thermique de l'atome est  kBTk_B \:T  (où  kBk_B  est la constante de Boltzman et  TT  la température), montrer que ceci explique l'origine de la dilatation du cristal.


Oscillation au voisinage d'un équilibre

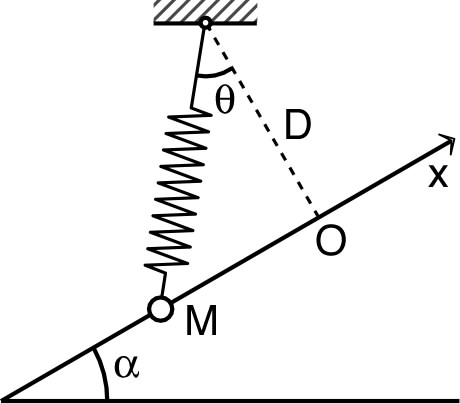
1.     • Dans le dispositif ci-contre, le mobile MM a une masse mm , le ressort a une raideur kk et une longueur “à vide”  L0<DL_0<D  (il reste tendu).
        a) Montrer que la longueur du ressort peut s'exprimer sous la forme :
L(θ)=(Rsin(θ))2+(D+R−Rcos(θ))2L(θ)=\sqrt{\left(R \:\sin(θ) \right)^2+\left(D+R-R \:\cos(θ) \right)^2\,} .
        b) En raisonnant à l'aide de l'énergie potentielle, déterminer les positions d'équilibre.
        c) Déterminer la stabilité de chacun de ces équilibres.
        d) On suppose vérifiée la condition :  (1−L0D)(D+R)>mgk\displaystyle \left(1-\frac{L_0}{D}\right)\,(D+R)>\frac{m \:g}{k} .  Déterminer la raideur KK de l'oscillateur et la période des petites oscillations autour de la position d'équilibre stable.
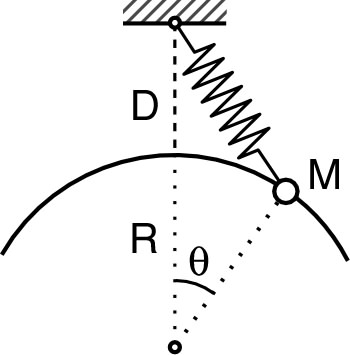dynOscLibres_ex_Im/dynOscLibres_ex_Im2.jpg

2.     • Dans le dispositif ci-contre, le mobile MM a une masse mm , le ressort a une raideur kk et une longueur “à vide”  L0=DL_0=D  (il reste tendu).
        a) Exprimer la longueur du ressort en fonction de DD et θθ , puis en fonction de xx et θθ .
        b) En posant  λ=mgsin(α)kL0\displaystyle λ=\frac{m \:g \:\sin(α)}{k \:L_0}  et en raisonnant à l'aide de l'énergie potentielle, exprimée en fonction de θθ , montrer que les positions d'équilibre sont solution de l'équation :  tan(θ)=sin(θ)+λ\tan(θ)=\sin(θ)+λ .
        c) Justifier qu'il existe une et une seule solution ; effectuer l'application numérique pour  λ=1λ=1 .
        d) Déterminer la stabilité de l'équilibre (pour λλ quelconque).
dynOscLibres_ex_Im/dynOscLibres_ex_Im3.jpg
        e) Déterminer la raideur KK de l'oscillateur et la période des petites oscillations.


Amortissement et viscosité

        • Dans un liquide dont le coefficient de viscosité est  ηη , une sphère de rayon  rr  et animée d'une vitesse  v→\overset{→}{v}  est soumise à une force de frottement visqueux (pour les faibles vitesses) :  f→=−6πηrv→\overset{→}{f}=-6π \:η \:r \:\overset{→}{v} .  Une telle sphère, de masse mm , est suspendue à un ressort de raideur  kk . La période d'oscillation dans l'air (où le frottement est négligeable) est  T0T_0 ; la pseudo-période dans le liquide est  TT .
        • Indiquer l'expression de ηη en fonction des caractéristiques de la sphère, de T0T_0 et TT .
        • Exprimer le décrément logarithmique δδ du mouvement (diminution du logarithme de l’amplitude pour une pseudo-période) en fonction des caractéristiques de la sphère, de ηη et TT .


Amortissement et facteur de qualité

1.     • On considère un oscillateur harmonique très faiblement amorti ; exprimer le facteur de qualité 𝒬𝒬 en fonction du décrément logarithmique δδ (diminution du logarithme de l’amplitude pour une pseudo-période).

2.     • On observe qu'après  nn  oscillations de pseudo-période TT voisine de T0T_0 , l'amplitude du mouvement n'est plus que le dixième de l'amplitude initiale ; exprimer le facteur de qualité 𝒬𝒬 en fonction de nn .


Diagrammes de phase

        • Tracer le diagramme de phase  ( x˙ω0\displaystyle \frac{\dot{x}}{ω_0}  en fonction de  xx ) pour les oscillations libres suivantes :
        a) oscillateur harmonique non amorti ;
        b) oscillateur harmonique amorti par frottement solide ;
        c) pendule pesant non amorti.



B. EXERCICES D’APPROFONDISSEMENT

Amortissement par courants de Foucault

        • Un cadre carré de côté AA est placé dans le plan vertical OxzOxz , ses côtés étant parallèles aux axes. Ce cadre, de masse mm , est constitué par un fil de résistance électrique RR ; il est mobile suivant OzOz et suspendu à un ressort de raideur kk de telle sorte que son centre est à l'équilibre en OO . Un champ magnétique uniforme B→\overset{→}{B} parallèle à OyOy (orthogonal) est appliqué dans la région où  z>0z>0 ; les mouvements du cadre sont tels qu'il n'est jamais entièrement intérieur, ni entièrement extérieur à cette zone. En supposant qu'on provoque des oscillations, faiblement amorties par les courants de Foucault, calculer le décrément logarithmique (diminution du logarithme de l’amplitude pour une pseudo-période).


Oscillateur à trois dimensions

        • On considère un oscillateur correspondant à un point matériel dont l’énergie potentielle peut s’écrire sous une forme générale :  Ep=Ep(x,y,z)E_p=E_p (x,y,z) .
        • En notant  (x,y,z) (x,y,z)  par  xix_i  avec  i=1;2;3i=1 \,;2 \,;3  on suppose que cette expression peut se développer sous une forme généralisée :  Ep(M)≈Ep(M0)+∇→Ep(M0)⋅M0M⟶ + 12 ∑ij (∂2Ep∂xi∂xj(M0).(xi−xi0)(xj−xj0)) \displaystyle E_p (M)≈E_p (M_0 )+\overset{→}{∇}E_p (M_0 )⋅\overset{⟶}{M_0 M}+\frac{1}{2}\, ∑_{ij} \left(\frac{∂^2 E_p}{∂x_i ∂x_j} (M_0 ) .(x_i-x_{i0} )(x_j-x_{j0} )\right) .
        • On suppose en outre qu’il est possible de choisir la direction des axes de façon à “diagonaliser” le second ordre :  Ep(M)≈Ep(M0)+∇→Ep(M0)⋅M0M⟶ + 12 ∑i (Ki(M0).(xi−xi0)2) \displaystyle E_p (M)≈E_p (M_0 )+\overset{→}{∇}E_p (M_0 )⋅\overset{⟶}{M_0 M}+\frac{1}{2} \,∑_i \left(K_i (M_0 ) .(x_i-x_{i0} )^2 \right)   avec   Ki= ∂2Ep ∂xi 2 ( M0 ) \displaystyle K_i=\frac{∂^2 E_p}{{∂x_i}^2} (M_0 ) .

1.     • Indiquer les conditions d’équilibre (stables et/ou instables).

2.     a) Étudier les petits mouvements au voisinage d’un équilibre stable.
        b) Préciser dans le cas où les constantes KiK_i sont égales.