M. VI - DYNAMIQUE ; ROTATIONS


Moment cinétique

• La mécanique du point peut être décrite sans rotation :  toute “rotation” d’un point est une translation curviligne (un point ne tourne pas sur lui même).

La description sous forme de rotation est alors équivalente à celle qui considère les translations, mais elle peut être utile pour simplifier certains calculs en les réexprimant autrement.

• On peut ainsi définir le “moment cinétique” d’un point matériel MM par rapport à un point OO (qui n’est pas forcément l’origine du repère) :  L→O=OM⟶×p→\overset{→}{L}_O=\overset{⟶}{OM}×\overset{→}{p}  où p→\overset{→}{p} est la quantité de mouvement de MM .

On peut en outre définir le “moment cinétique algébrique” d’un point MM par rapport à un axe orienté ΔΔ (arbitraire) :  L¯Δ=L→O⋅u→Δ\widebar{L}_Δ=\overset{→}{L}_O⋅\overset{→}{u}_Δ  où u→Δ\overset{→}{u}_Δ est un vecteur unitaire orienté selon ΔΔ et où OO est un point quelconque de ΔΔ .

◊ remarque : le choix judicieux (arbitraire) du point OO référence des moments peut simplifier les calculs.

Moments des forces

• On peut définir d’une façon analogue le “moment” (par rapport à un point OO , qui n’est pas forcément l’origine du repère) d’une force F→\overset{→}{F} appliquée à un point matériel MM :  ℳ→O=OM⟶×F→\overset{→}{ℳ}_O=\overset{⟶}{OM}×\overset{→}{F} .

On peut de même définir le “moment algébrique” par rapport à un axe orienté ΔΔ (arbitraire) :  ℳ¯Δ=ℳ→O⋅u→Δ\widebar{ℳ}_Δ=\overset{→}{ℳ}_O⋅\overset{→}{u}_Δ  où u→Δ\overset{→}{u}_Δ est un vecteur unitaire orienté selon ΔΔ et où OO est un point quelconque de ΔΔ .

Théorème du moment cinétique

• Dans de nombreux cas (mais pas tous), le mouvement peut alors être décrit par le théorème du moment cinétique :  ∑ℳ→O=dL→Odt\displaystyle ∑ \overset{→}{ℳ}_O =\frac{d\overset{→}{L}_O}{dt}  ;  ou bien en projection sur un axe :  ∑M¯Δ=dL¯Δdt\displaystyle ∑ \widebar{M}_Δ =\frac{d\widebar{L}_Δ}{dt} .

En effet :  dL→Odt=∑(OM⟶×F→)+(v→M−v→O)×p→\displaystyle \frac{d\overset{→}{L}_O}{dt}=∑ \left(\overset{⟶}{OM}×\overset{→}{F} \right) +(\overset{→}{v}_M-\overset{→}{v}_O ) ×\overset{→}{p}  ;  or  v→M×p→=0→\overset{→}{v}_M ×\overset{→}{p}=\overset{→}{0} ,  d'où la relation précédente quand  v→O∥v→M\overset{→}{v}_O ∥ \overset{→}{v}_M  (et en particulier si OO est fixe).

◊ remarque : cette relation ne fournit une information supplémentaire que pour le cas d’un système complexe ; pour un point matériel elle équivaut au principe fondamental de la dynamique.

◊ remarque : pour un point en rotation autour d’un point OO (à distance  OM=rOM=r  constante), on obtient :  OM⟶×v→=r2ω→\overset{⟶}{OM} ×\overset{→}{v}=r^2 \; \overset{→}{ω}  ;  on peut alors définir un “moment d’inertie”  J=mr2J=m\: r^2  et écrire :  ∑ℳ→O=Jdω→dt\displaystyle ∑ \overset{→}{ℳ}_O =J \:\frac{d\overset{→}{ω}}{dt}  (analogue à  ∑F→=mdv→dt\displaystyle ∑ \overset{→}{F} =m \:\frac{d\overset{→}{v}}{dt} ,  mais cette relation n’est valable que dans ce cas très particulier).

Exemples d’applications

Mouvements à force centrale

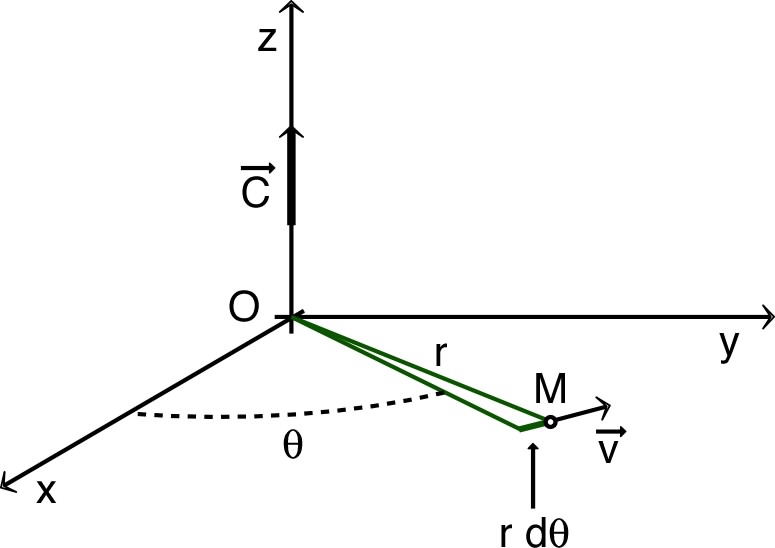
• Dans ce cas, avec OO fixe :
∑ℳ→O=OM⟶×F→=0→{\displaystyle ∑ \overset{→}{ℳ}_O }=\overset{⟶}{OM} ×\overset{→}{F}=\overset{→}{0}
et  L→O=OM⟶×p→\overset{→}{L}_O=\overset{⟶}{OM} ×\overset{→}{p}  est constant.

Puisque OM⟶\overset{⟶}{OM} reste perpendiculaire à L→O\overset{→}{L}_O , le mouvement de MM se fait dans le plan perpendiculaire à L→O\overset{→}{L}_O et contenant OO .
dynRot_Im/dynRot_Im2.jpg

En coordonnées polaires dans le plan du mouvement :
OM⟶=ru→r\overset{⟶}{OM}=r \;\overset{→}{u}_r   ;   v→=r˙u→r+rθ˙u→θ\overset{→}{v}=\dot{r} \; \overset{→}{u}_r+r \:\dot{θ} \; \overset{→}{u}_θ   ;   L→O=mr2θ˙u→z\overset{→}{L}_O=m \:r^2 \: \dot{θ} \; \overset{→}{u}_z  ;
donc la quantité  C=r2θ˙C=r^2 \: \dot{θ}  est constante.

• La “vitesse aréolaire” (vitesse algébrique de “balayage” de l’aire par OMOM ) est :  S˙=12r2θ̈=C2\displaystyle \dot{S}=\frac{1}{2}r^2 \: \ddot{θ}=\frac{C}{2}  ;  la constance de cette vitesse aréolaire pour les mouvements à accélération centrale est appelée “loi des aires”.

◊ remarque : il faut ne pas confondre l’aire SS et l’abscisse curviligne ss .

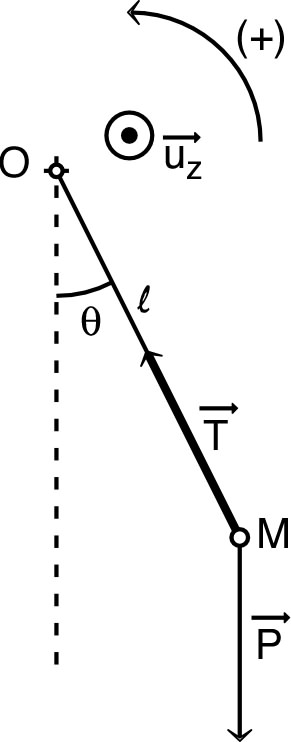
Pendule simple

• En se limitant au mouvement dans un plan vertical :
L→O=OM⟶×p→=m𝓁2θ˙u→z\overset{→}{L}_O=\overset{⟶}{OM} ×\overset{→}{p}=m\: 𝓁^2 \: \dot{θ} \; \overset{→}{u}_z
et     ∑ℳ→O=OM⟶×(T→+P→)=−mg𝓁sin(θ)u→z{\displaystyle ∑ \overset{→}{ℳ}_O} =\overset{⟶}{OM} × \left(\overset{→}{T}+\overset{→}{P} \right)=-m \:g\: 𝓁 \; \sin(θ) \; \overset{→}{u}_z  ;
c’est-à-dire algébriquement (avec  u→Δ=u→z\overset{→}{u}_Δ=\overset{→}{u}_z ) :
L¯Δ=m𝓁2θ˙\widebar{L}_Δ=m \:𝓁^2 \: \dot{θ}   et   ∑ℳ¯Δ=−mg𝓁sin(θ){\displaystyle ∑ \widebar{ℳ}_Δ} =-m \:g \:𝓁 \; \sin(θ) .

Puisque OO est fixe :  dL¯Δdt=∑ℳ¯Δ\displaystyle \frac{d\widebar{L}_Δ}{dt}=∑\,\widebar{ℳ}_Δ   c’est-à-dire :
θ̈+g𝓁sin(θ)=0\displaystyle \ddot{θ}+\frac{g}{𝓁} \: \sin(θ)=0 .

Pour les petites amplitudes ( θ≤20°θ≤20 \:° ) :  θ̈+g𝓁θ≈0\displaystyle \ddot{θ}+\frac{g}{𝓁} \: θ≈0  d’où :  θ=Θmcos(ωt+ϕ)θ=Θ_m \; \cos(ω \,t+ϕ)  avec  ω=g𝓁\displaystyle ω=\sqrt{\frac{g}{𝓁}} .
dynRot_Im/dynRot_Im1.jpg

◊ remarque : si le pendule est lâché immobile, le mouvement débute dans le plan vertical contenant OO et MM (les forces sont dans ce plan) ; mais si le mouvement est dans un plan vertical contenant OO , alors  L→O∥∑ℳ→O=L→˙O\overset{→}{L}_O ∥ ∑\,\overset{→}{ℳ}_O =\dot{\overset{→}{L}}_O  donc le mouvement reste dans ce plan (perpendiculaire à L→O\overset{→}{L}_O ).

📖 exercices n° I, II et III.

Travail d'une force lors d'un mouvement circulaire

• Pour un point en mouvement circulaire (par rapport à un point fixe OO quelconque sur un axe de rotation ΔΔ ) le travail  d'une force F→\overset{→}{F} peut s'exprimer en fonction de son moment :
δW=ℳ¯Δdθ=ℳ→O⋅ω→dt=(OM⟶×F→)⋅ω→dt=(ω→×OM⟶)⋅F→dt=v→⋅F→dtδW=\widebar{ℳ}_Δ \: dθ=\overset{→}{ℳ}_O⋅\overset{→}{ω} \: dt=\left(\overset{⟶}{OM} ×\overset{→}{F} \right)⋅\overset{→}{ω} \: dt=\left(\overset{→}{ω} ×\overset{⟶}{OM} \right)⋅\overset{→}{F} \: dt=\overset{→}{v}⋅\overset{→}{F} \: dt .

◊ remarque : on note généralement  ω→=θ˙u→Δ\overset{→}{ω}=\dot{θ}\; \overset{→}{u}_Δ  ;  par ailleurs pour un vecteur OM⟶\overset{⟶}{OM} de norme constante :  dOM⟶dθ=u→Δ×OM⟶\displaystyle \frac{d\overset{⟶}{OM}}{dθ}=\overset{→}{u}_Δ × \overset{⟶}{OM} .

◊ remarque : le produit mixte est invariant par “permutation circulaire” :
(A→×B→)⋅C→=(C→×A→)⋅B→=(B→×C→)⋅A→\left(\overset{→}{A} ×\overset{→}{B} \right)⋅\overset{→}{C}= \left(\overset{→}{C} ×\overset{→}{A} \right)⋅\overset{→}{B}= \left(\overset{→}{B} ×\overset{→}{C} \right)⋅\overset{→}{A} .