DYNAMIQUE - ROTATIONS - corrigé des exercices

A. EXERCICES DE BASE

Conservation du moment cinétique

• L’énergie cinétique initiale est :

E_c=\frac{1}{2} m \:v_0^{\:2}

.
• Le moment cinétique initial est :

\overset{→}{L}_O=m \:\overset{⟶}{OM}× \overset{→}{v}_0=m \,.(r \:\overset{→}{u}_r ) × (\widebar{v} _0 \: \overset{→}{u}_θ )

où

\widebar{v}_0=r_0 \: ω_0

est comptée algébriquement le long du cercle. Ceci donne :

\overset{→}{L}_O=m \:r_0^{\:2} \: ω_0 \: \overset{→}{u}_z

et on peut utiliser la mesure algébrique (moment par rapport à l’axe perpendiculaire au plan et passant par O ) :

\widebar{L}_Δ=m \:r_0^{\:2} \: ω_0

2.a.	• La seule force à prendre en compte est la traction $\overset{→}{T}$ du fil car le poids et la réaction du support (sans frottement) sont perpendiculaires au plan et se compensent. La force $\overset{→}{T}$ travaille, donc l’énergie cinétique varie... Par contre $\overset{→}{T}$ est une force centrale, donc de moment nul par rapport à $O$ , ainsi d’après la loi de la dynamique de rotation : $\displaystyle \frac{d\overset{→}{L}_O}{dt}=\overset{→}{ℳ}_O=\overset{→}{0}$ on en déduit que le moment cinétique est invariant.

2.b.	• Si on cherche la nouvelle vitesse de rotation $ω_1$ pour une nouvelle valeur $r=r_1$ fixée, on peut écrire la conservation de $\widebar{L}_Δ$ : $m \:r_1^{\:2} \: ω_1=m \:r_0^{\:2} \: ω_0$ c’est-à-dire : $\displaystyle ω_1=\frac{r_0^{\:2}}{r_1^{\:2}} \: ω_0$ .

2.c.	• Le travail fourni par la traction $\overset{→}{T}$ n’est pas facile à calculer avec la relation de définition : $W=∫ δW=∫\: \overset{→}{T}⋅d\overset{⟶}{OM}=∫\: \overset{→}{T}⋅\overset{→}{u}_r \: dr=-∫ T(r) \:dr$ car l’expression de $T(r)$ dépend de la rapidité avec laquelle on passe de $r_0$ à $r_1$ . • Par contre le calcul est simple avec le théorème de l’énergie cinétique : $\displaystyle E_{c1}=\frac{1}{2} m \:v_1^{\:2}=\frac{1}{2} m \:r_1^{\:2} \: ω_1^{\:2}=\frac{1}{2} \left(m \:r_1^{\:2} \: ω_1 \right)\: ω_1=\frac{1}{2}\left (m \:r_0^{\:2} \: ω_0 \right) \: ω_1=\frac{1}{2} m \:r_0^{\:2} \: ω_0^{\:2} \: \frac{r_0^{\:2}}{r_1^{\:2}}$ ; $\displaystyle W=ΔE_c=\frac{1}{2} m \:v_0^{\:2} \: \frac{r_0^{\:2}}{r_1^{\:2}}-\frac{1}{2} m \:v_0^{\:2}=\frac{1}{2} m \:v_0^{\:2} .\left(\frac{r_0^{\:2}}{r_1^{\:2}}-1\right)$ . ◊ remarque : si le point $M$ passe par la distance $r_1$ sans y être stabilisé (pour une tension telle que $r$ continue à diminuer), alors le calcul précédent doit tenir compte de la coordonnée $v_{1r}=\dot{r}$ (car $ω_1$ ne donne que $v_{1θ}=r_1 \: ω_1$ ).

Oscillation au voisinage d'un équilibre

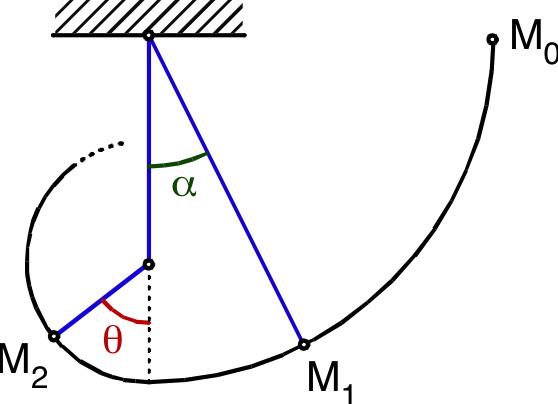
• En supposant que la position “à vide” du ressort correspond à

θ=0

, la masse

m

est soumise à un moment de rappel :

ℳ=-C \:θ

correspondant à une énergie potentielle élastique :

E_{pe}=\frac{1}{2} C \:θ^2

. L'expression de cette énergie potentielle peut se retrouver en sachant que, lors d'une rotation

dθ

, le travail d'une force de moment

ℳ

peut s'écrire

δW=ℳ \:dθ=-C \:θ \:dθ=-dE_{pe}

.
• L’énergie potentielle de pesanteur étant par ailleurs :

E_{pp}=m \:g \:z=m \:g \:𝓁 \; \cos(θ)

, on peut écrire l’énergie mécanique sous la forme :

E_m=\frac{1}{2} m \:𝓁^2 \: \dot{θ}^2+\frac{1}{2} C \:θ^2+m \:g \:𝓁 \; \cos(θ)

.
• Les positions d’équilibre correspondent à :

\displaystyle \frac{dE_p}{dθ}=C \:θ-m \:g \:𝓁 \; \sin(θ)=0

; il y a donc un équilibre évident pour

θ=0

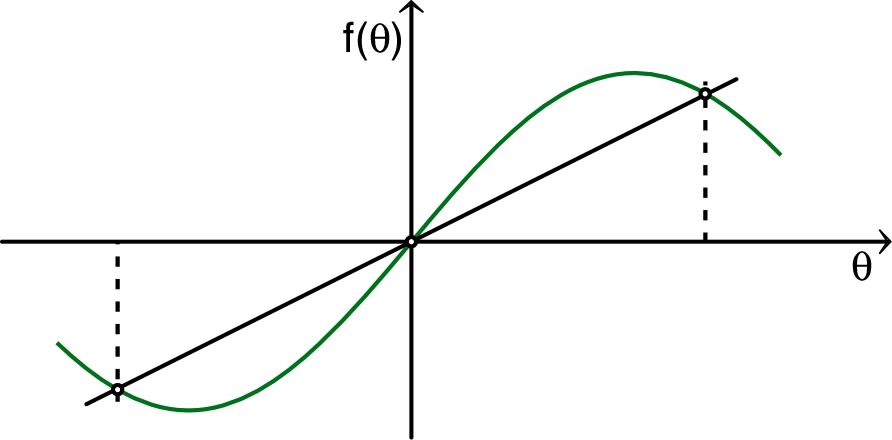
. La comparaison graphique des fonctions :

f_1 (θ)=C \:θ

f_2 (θ)=m \:g \:𝓁 \; \sin(θ)

montre par ailleurs qu’il existe une autre position d’équilibre

θ∈[0\,,\,π]

(en fait : une de chaque côté, par symétrie) si et seulement si :

C<m \:g \:𝓁

(droite de pente inférieure à la pente à l’origine de la sinusoïde).

• L’équilibre est stable si et seulement si la dérivée seconde (égale dans ce cas à la “raideur” de l’oscillateur) est positive :

\displaystyle \frac{d^2 E_p}{dθ^2} =C-m \:g \:𝓁 \; \cos(θ)>0

. Les pentes du graphique précédent montrent alors clairement que :

si $C>m \:g \:𝓁$ il y a un seul équilibre, stable, pour $θ=0$ ; la raideur est : $K=C-m \:g \:𝓁$ ;
si $C<m \:g \:𝓁$ il y a un équilibre instable pour $θ=0$ et un équilibre stable pour $θ_e≠0$ solution de : $C \:θ_e=m \:g \:𝓁 \; \sin(θ_e )$ ; par rapport à la variable $θ$ , la raideur est : $K=C-m \:g \:𝓁 \; \cos(θ_e )$ .

◊ remarque : pour

C=m \:g\: 𝓁

il y a une seule position d’équilibre, stable, pour

θ=0

, mais la raideur de l’oscillateur est alors nulle ; il s’agit d’un oscillateur anharmonique dont le mouvement ne peut pas être étudié aussi simplement : la période des oscillations dépend de leur amplitude (et la période des petites oscillations tend vers l’infini).
• L’équation du mouvement découle de la propriété :

\displaystyle \frac{dE_m}{dt}=\dot{θ} \: \frac{dE_m}{dθ}=0

; l’étude du mouvement correspondant à

\dot{θ}≠0

; l’équation du mouvement est :

\displaystyle \frac{dE_m}{dθ}=m \:𝓁^2 \: \ddot{θ}+C \:θ-m \:g \:𝓁 \; \sin(θ)=0

.
• En effectuant un développement limité au voisinage de l’équilibre, pris comme origine (

Θ=θ-θ_e

), l’équation précédente se met sous la forme :

m \:𝓁^2 \: \ddot{Θ}+K \:Θ=0

. La période des petites oscillations est par conséquent :

\displaystyle T=2π \sqrt{\frac{m\: 𝓁^2}{K}}

.
◊ remarque : en utilisant une abscisse curviligne

S=s-s_e=𝓁 \:Θ

, on obtient :

\displaystyle K'=\frac{C-m \:g \:𝓁 \;\cos\left(\frac{s_e}{𝓁}\right)}{𝓁^2}

\displaystyle T=2π \,\sqrt{\frac{m}{K'}}

Théorème du moment cinétique

• On peut raisonner avec le moment cinétique (par rapport au point

A

) ; la tension des tiges a un moment nul (avant et pendant le choc), le poids a un moment nul pendant le choc, donc le moment cinétique

\overset{→}{L}_A=\overset{⟶}{AM} × m \:\overset{→}{v}=m .\left(𝓁+𝓁'\right) \: v \;\overset{→}{u}_y

(vers l'arrière du plan du mouvement) est conservé pendant le choc ; par suite la norme du vecteur vitesse est conservée.
◊ remarque : ceci peut se déduire aussi du théorème de l'énergie cinétique.
• Compte tenu de la quasi-instantanéité du choc, on peut considérer que la vitesse reste horizontale (perpendiculaire à la seconde tige), donc le vecteur vitesse est conservé lors du choc.

• Le problème se ramène à celui d’une fronde de longueur

𝓁'

dont le mobile est lancé dans la position d’équilibre avec une vitesse

v_0

qui est celle atteinte par

M

lors du choc.
• D’après le théorème du moment cinétique entre l’instant initial et l’instant du choc, sachant que la traction exercée par la tige a un moment nul :

$\dot{\overset{→}{L}}_A=\overset{→}{ℳ}_A (\overset{→}{P})$ ; $m .\left(𝓁+𝓁'\right)^2 \, \ddot{α} \; \overset{→}{u}_y=-m \:g .\left(𝓁+𝓁'\right) \; \sin(α) \; \overset{→}{u}_y$ ;
$m .\left(𝓁+𝓁'\right) \: \dot{α} \: \ddot{α}-m \:g \; \sin(α) \: \dot{α}=0$ ; $\displaystyle \frac{d}{dt} \left[\frac{1}{2} \left(𝓁+𝓁'\right) \: \dot{α}^2-g \:\cos(α) \right] = 0$ ;
$\frac{1}{2} \left(𝓁+𝓁'\right) \: \dot{α}_0^{\:2}-g=-g \: \cos\left(\frac{π}{2}\right)=0$ ; $v_0=\left(𝓁+𝓁'\right) \: \dot{α}_0=\sqrt{2 \,g .\left(𝓁+𝓁'\right)}$ .

• De même, d’après le théorème du moment cinétique entre l’instant du choc et un instant quelconque précédant le passage au sommet :

$\dot{\overset{→}{L}}_O=\overset{→}{ℳ}_O (\overset{→}{P})$ ; $m .{𝓁'}^2 \: \ddot{θ}\; \overset{→}{u}_y=-m \:g \:𝓁' \; \sin(θ) \; \overset{→}{u}_y$ ; $\displaystyle \frac{d}{dt} \left[\frac{1}{2}𝓁' \:\dot{θ}^2-g \;\cos(θ) \right]=0$ ;
$\frac{1}{2}𝓁' \:\dot{θ}^2=\frac{1}{2}𝓁'\: \dot{θ}_0^{\:2}-g .[1-\cos(θ) ]$ ; $𝓁' \:\dot{θ}_0=v_0=\left(𝓁+𝓁'\right) \: \dot{α}_0$ .

◊ remarque : on garde la même convention algébrique pour l'orientation des angles, ce qui correspond à

θ<0

sur l'exemple du dessin.
• En particulier lors du passage au sommet (s’il est atteint) :

\frac{1}{2}𝓁' \:\dot{θ}^2=\frac{1}{2}𝓁' \:\dot{θ}_0^{\:2}-2 \,g

; par suite une condition nécessaire pour que le sommet soit atteint est :

\dot{θ}>0

et donc :

v_0>\sqrt{4 \,g \:𝓁'}

.
• On aboutit ainsi à la condition :

2 \,g .\left(𝓁+𝓁'\right)>4 \,g \:𝓁'

c'est-à-dire

𝓁>𝓁'

.
◊ remarque : il faut aussi probablement

𝓁>𝓁'

pour éviter que le point

M

percute le support comportant la fixation en

A

(la suite du mouvement nécessite d'ailleurs que la rotule permette de dépasser ce point), mais cette condition est automatiquement vérifiée dans le cas précédent.

B. EXERCICE D'APPROFONDISSEMENT

Équilibre relatif d'une bicyclette

• Lorsque la bicyclette commence à pencher vers la droite, son centre d'inertie se décale par rapport à la ligne d'avancée des roues au sol. Faute de rétablissement, la pesanteur cause alors un moment de force qui tend à augmenter l'inclinaison ; un rétablissement est nécessaire.
• Si on admet que le guidon tourne à droite lorsque la bicyclette penche à droite, alors (puisque la bicyclette avance) le point de contact de la roue avant se déplace vers la droite. Si ce déplacement est suffisant (d'autant plus rapide que la bicyclette avance vite), les points d'appui au sol repassent à droite du centre de gravité ; la pesanteur tend alors à faire incliner vers la gauche, donc le guidon tourne à gauche (... et ainsi de suite).

• La roue avant a (par rapport à son centre) un moment cinétique

\overset{→}{L}

horizontal vers la gauche.
◊ remarque : si la bicyclette ne se déplace pas exactement d'un mouvement rectiligne uniforme, le référentiel associé au centre de la roue n'est pas tout à fait galiléen, mais on peut montrer que pour un système de points matériels (donc entre autres une roue) le théorème du moment cinétique est valide par rapport au centre d'inertie, même si le mouvement de ce dernier n'est pas rectiligne uniforme.
• Lorsque la bicyclette penche à droite, la pesanteur de la roue et la réaction du sol (ainsi que l'action de la fourche avant de la bicyclette, qui tend à entraîner la roue dans son inclinaison d'ensemble) causent un moment de force orienté vers l'avant.

• Le théorème du moment cinétique dit alors que le moment cinétique

\overset{→}{L}

de la roue a dans ce cas tendance à varier vers l'avant (selon le moment des forces). Mais, pour un moment cinétique orienté vers la gauche, une modification vers l'avant correspond à une “rotation” vers la droite : la roue avant tend donc spontanément à pivoter vers la droite (ainsi que le guidon qui lui est solidaire).

◊ remarque : la roue arrière subit le même effet mais elle ne peut pas pivoter car elle est solidaire du cadre de la bicyclette.

3.a.

• Lorsque la bicyclette s'incline vers la droite, la réaction du sol (qui, en l'absence de virage, reste verticale) a une droite d'action passant à gauche de l'axe du guidon. Compte tenu de l'inclinaison de cet axe, ceci provoque un moment de force tendant à faire tourner le guidon (si la réaction était parallèle à l'axe, le moment serait nul).
• De plus, puisque le point de contact est en arrière de l'axe, le moment tend à faire tourner le guidon à droite (donc tend à provoquer le rétablissement du vélo, s'il avance).

3.b.

• Lorsqu'on appuie sur le pédalier, le cadre du vélo “traîne” la roue avant (retenue par les frottements au sol, en un point situé en arrière de l'axe du guidon). Si le guidon a tourné à droite, le moment du frottement au sol est dans le sens tendant à redresser la roue : cela atténue l'effet décrit à la question (3.a), d'autant plus que le guidon a tourné (évitant ainsi qu'il tourne trop).
◊ remarque : dans ce cas, le frottement du sol sur la roue arrière est vers l'avant car c'est la roue motrice, mais celui sur la roue avant est vers l'arrière car elle est traînée par le cadre.
◊ remarque : cet effet (souvent appelé “effet de chasse”) est analogue à celui observé sur les roues de chariots de supermarché (avec un axe de fourche vertical décalé du centre de la roue) : dès qu'on pousse le chariot, chaque roue tend à se placer spontanément en arrière de l'axe de fourche.
◊ remarque : si le vélo roulait à l'envers (en reculant), cela tendrait au contraire à amplifier la rotation du guidon, ce qui conduirait rapidement à la chute.

• Tout contrepoids placé à l'avant de l'axe du guidon tend (par l'effet de la pesanteur) à le faire tourner du côté où la bicyclette s'incline. Entre autres sont disposés ainsi la partie courbe de la fourche avant et le centre d'inertie de la roue avant, mais généralement aussi le guidon lui même. Cet effet intervient souvent de façon importante dans le maintien de l'équilibre relatif (au moins autant que celui envisagé à la question (3.a)).
◊ remarque : en fait, c'est la répartition d'ensemble des masses de la bicyclette qui intervient ; on peut même (bien que cela ne soit ni simple à faire, ni pratique à utiliser) construire un vélo avec appui au sol en avant de l'axe du guidon, mais dont la répartition des masses est telle que l'équilibre relatif se maintient.

• Toutefois, les effets de rotation du guidon conduisent ainsi à des oscillations autour de la position verticale : lorsque le guidon tourne et que le vélo avance, cela fait repasser le point d'appui de l'autre côté du centre d'inertie, ce qui fait pencher le vélo de l'autre côté, donc fait tourner le guidon dans l'autre sens, etc.
• En présence d'un contrepoids trop important, l'effet peut devenir tellement important que ces oscillation s'amplifient : il devient quasi impossible de maintenir l'équilibre relatif du vélo... à moins de pédaler assez vigoureusement pour atténuer le phénomène (selon le mécanisme “de chasse” décrit à la question (3.b)).
◊ remarque : la courbure du bas de la fourche avant sert ainsi, entre autres, à doser les effets pour mieux contrôler l'équilibre relatif.
☞ remarque : ceux qui veulent faire des expérimentations doivent le faire avec prudence en un lieu sans danger.