DYNAMIQUE - ROTATIONS - exercices


A. EXERCICES DE BASE

Conservation du moment cinétique

        • Un point matériel MM , de masse mm , glisse sans frottement sur un plan horizontal PP . Il est fixé à l’extrémité d’un fil passant par un trou quasi-ponctuel en un point OO du plan.

1.     • Le point MM est initialement animé d’un mouvement circulaire uniforme de vitesse v0v_0 avec  OM=r0OM=r_0  (l’autre extrémité du fil est fixée). Exprimer l’énergie cinétique de MM ainsi que son moment cinétique par rapport à OO .

2.     • On tire sur l’autre extrémité du fil de manière à diminuer la longueur jusqu’à  OM=r1<r0OM=r_1<r_0 .
        a) Quelles sont les quantités invariantes lors de cette transformation ?
        b) Quelle est la nouvelle vitesse angulaire ω1ω_1 de MM ?
        c) Quel a été le travail fourni au système lors de cette transformation ?


Oscillation au voisinage d'un équilibre

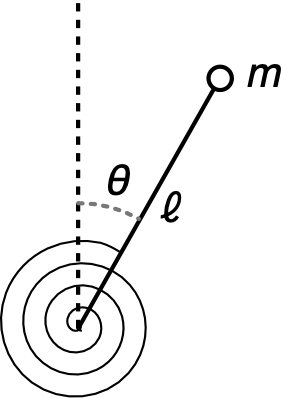
        • Dans un plan vertical on considère le dispositif suivant, constitué d'un point matériel de masse mm , fixé à l'extrémité d'une tige de longueur 𝓁𝓁 (de masse négligeable) en rotation autour de son autre extrémité.
        • Sur la tige est attaché un ressort spiral de raideur en torsion CC et de torsion “à vide”  θ0=0θ_0=0 ,  exerçant un moment de rappel algébrique :  ℳ=−C.(θ−θ0) ℳ=-C.(θ-θ_0) .
        • Déterminer la position d'équilibre, puis la raideur et la période des petites oscillations autour de l'équilibre.
dynRot_ex_Im/dynRot_ex_Im1.jpg


Théorème du moment cinétique

        • Un pendule est constitué d’un point matériel MM de masse mm suspendu à un point fixe AA par un assemblage de deux tiges de masse négligeable. Les deux tiges, de longueurs respectives 𝓁𝓁 et 𝓁′𝓁' , sont reliées bout à bout par une rotule sans frottement. On lâche le pendule avec une vitesse initiale nulle, les tiges (alignées) faisant un angle α0α_0 par rapport à la verticale.
        • Une barre horizontale est placée au dessous de AA , de sorte que la première tige heurte cette barre et se bloque lorsque le pendule passe par sa position d’équilibre. Le mouvement de la seconde tige reste alors possible.
dynRot_ex_Im/dynRot_ex_Im0.jpg

1.     • Montrer que la vitesse de MM se conserve pendant le choc.

2.     • En prenant  α0=π2α_0=\frac{π}{2} ,  déterminer la condition (sur 𝓁𝓁 et 𝓁′𝓁' ) pour que le pendule continue d'un mouvement de rotation sans rebroussement.


B. EXERCICE D'APPROFONDISSEMENT

Équilibre relatif d'une bicyclette

        ☞ remarque préalable : une roue de bicyclette en rotation n'est pas un “point matériel” (et la bicyclette en entier est encore moins simple) ; de tels systèmes sont étudiés ultérieurement (systèmes de points matériels, puis mécanique du solide) ; cet exercice est toutefois proposé ici (en approfondissement) pour essayer de mettre en évidence l'utilité des raisonnements avec le moment cinétique.

1.     • L'équilibre d'une bicyclette est relatif : par rapport au sol, quand la bicyclette penche d'un côté, le guidon tend à tourner dans le sens qui conduit à rétablir la verticalité. Préciser ce mouvement.
        ◊ remarque : il ne s'agit pas de justifier physiquement le mouvement (rotation du guidon), mais seulement ses conséquences (rétablissement de la verticalité).
        ◊ remarque : le raisonnement peut être fait dans le référentiel (non galiléen) de la bicyclette, mais il est ici plus simple de raisonner dans le référentiel (galiléen) lié au sol.

2.     • Justifier que le théorème du moment cinétique, appliqué à la roue avant, suggère une explication physique de la cause de rotation du guidon.

3.     • En réalité (sauf éventuellement pour une moto), le moment cinétique de la roue avant est trop faible et l'effet précédent (bien qu'agissant dans le bon sens) est généralement insuffisant.
        a) Les bicyclettes on “normalement” une fourche avant disposée de telle façon que le point de contact de la roue avant sur le sol soit en arrière de l'axe (incliné) du guidon. Justifier que, lors d'une inclinaison de la bicyclette, cela provoque l'apparition d'un moment de la force de réaction du sol, dans le sens tendant à faire tourner le guidon du côté correspondant.
        ◊ remarque : l'arrondi vers l'avant de la partie inférieure de la fourche avant tend à diminuer cet effet, mais il a une autre utilité (entre autres, de renforcer la résistance de la fourche aux cahots de la route).
        b) Justifier que l'appui sur les pédales tend à diminuer cet effet, d'où un moyen de le doser pour contrôler aisément l'équilibre relatif quand on lâche le guidon.

4.     • Ceux qui ont utilisé une sacoche fixée sur le guidon ont peut-être remarqué que, quand celle-ci est très chargée, l'équilibre relatif de la bicyclette est nettement plus difficile à maintenir (on ne peut pratiquement plus lâcher le guidon).
        • Justifier que, lors d'une inclinaison de la bicyclette, la présence d'un contrepoids à l'avant du guidon provoque l'apparition d'un moment de la force de pesanteur, dans un sens tendant à modifier le maintien de l'équilibre relatif, d'une façon qui peut l'améliorer ou le perturber selon la géométrie du dispositif de direction.