M. VII - DYNAMIQUE - PLANÈTES ET SATELLITES
Champs newtonien et coulombien
• La force de Newton entre deux points matériels
et
(masses
et
) :
(avec
et
)
est analogue à la loi coulombienne entre deux charges
et
:
(avec
).
On peut associer à la force électrostatique un
“champ électrostatique” causé par
en
:
;
on définit de même un “champ gravitationnel” causé par
en
:
.
◊ remarque : le champ gravitationnel (contribution principale de la
pesanteur) a une unité d’accélération.
• Les forces en
dérivent d’une énergie potentielle en
:
pour la loi
newtonienne ;
pour la loi coulombienne.
Les champs en
dérivent d’un potentiel en
:
(en
), tel que :
;
(en
), tel que :
.
☞ remarque : le théorème de Gauss (étudié en électrostatique)
s’applique aux champs de gravitation :
où
est la masse volumique
et où
est le
volume intérieur à la surface fermée
; ainsi, le
champ créé par une distribution de masse à symétrie sphérique, à
l’extérieur de celle-ci, est le même que si toute la masse était au
centre (propriété des champs en
).
Étude des trajectoires
Mouvement à accélération centrale
• On considère un mouvement causé par une force passant par un point
fixe choisi comme origine
.
• D’après la conservation du moment cinétique, le mouvement est plan
(dans le plan perpendiculaire à
) et suit la loi des aires.
En coordonnées cylindriques (polaires dans le plan du mouvement),
ceci s’écrit :
avec la
constante de la loi des aires :
.
• En repérant la trajectoire par
l’équation
obtenue par élimination du temps
, en
utilisant la variable
et en substituant
, on peut réexprimer la vitesse (“première formule de
Binet”) :
.
• D’une façon analogue, compte tenu du fait que
l’accélération centrale a une composante orthoradiale nulle
:
. En utilisant les mêmes notations que
précédemment, on obtient la “deuxième formule de
Binet” :
.
Propriétés générales
• On se propose d’étudier le mouvement d'un point
, de masse
, en
interaction avec un point
de
masse
.
On prend comme origine (notée
) la position
“fixe” de (≈ centre
d'inertie).
On considère une interaction de la forme :
(avec une constante
pour le cas répulsif et
pour le cas attractif).
• Pour une force centrale, la seconde formule de Binet donne :
puis :
.
La solution générale est de la forme :
où
et
sont des
constantes déterminées par les conditions initiales. Les
trajectoires correspondantes sont des coniques.
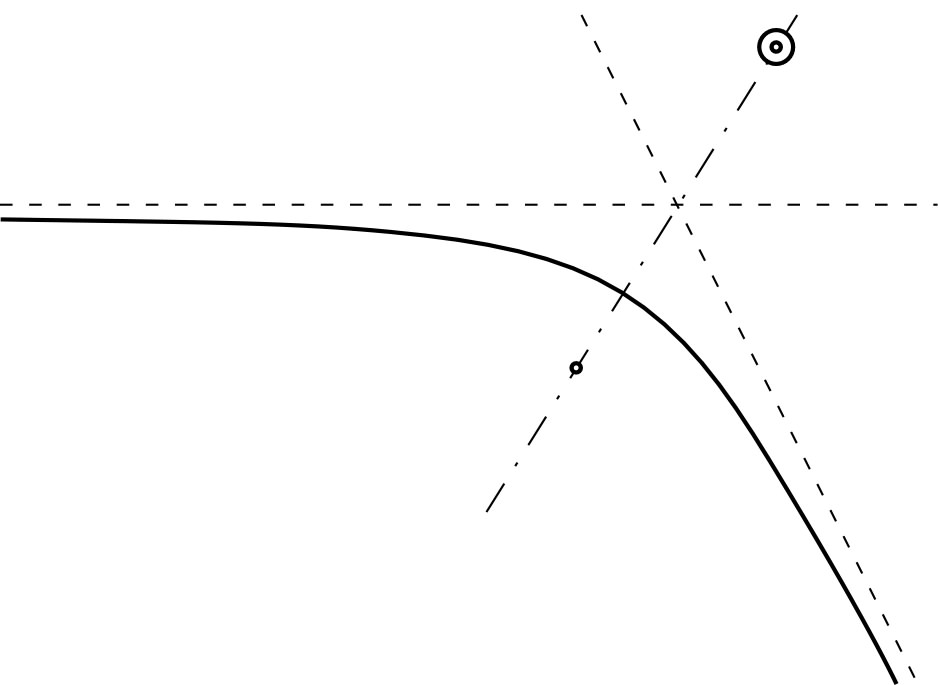
• Pour des forces répulsives (
),
les trajectoires sont des portions d’hyperboles ayant l’origine
comme foyer :
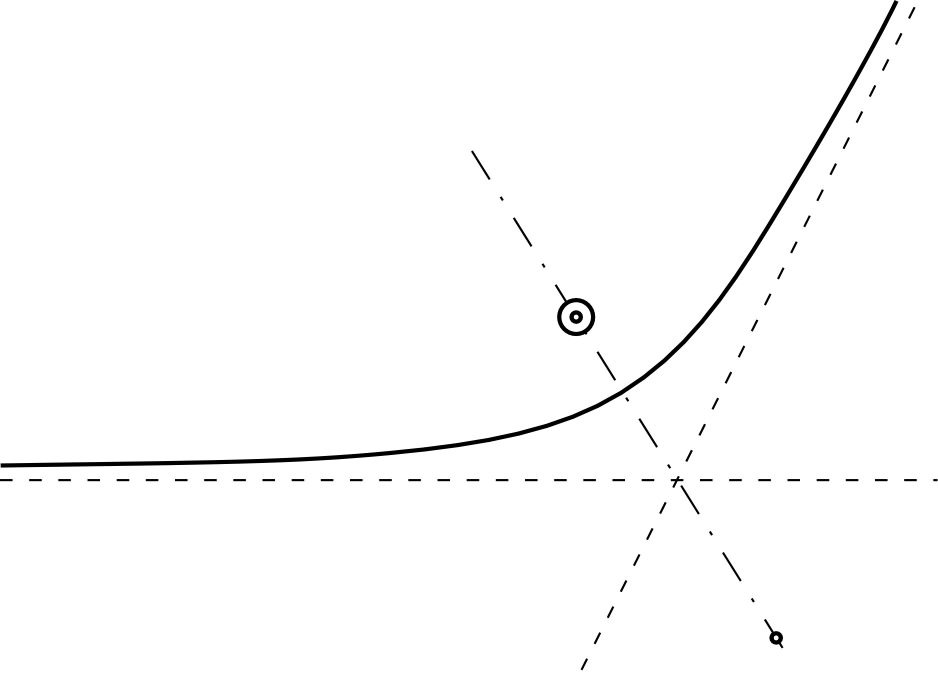
• Pour des forces attractives (
),
les trajectoires sont des portions d’hyperboles, d’ellipses, ou de
paraboles (cas limite intermédiaire) :
Mouvement des planètes et satellites
• Le mouvement des satellites correspond au cas attractif, entre
deux masses
et
(satellite),
avec :
.
La solution est :
où
et
sont nommés “excentricité” et “paramètre” de la trajectoire.
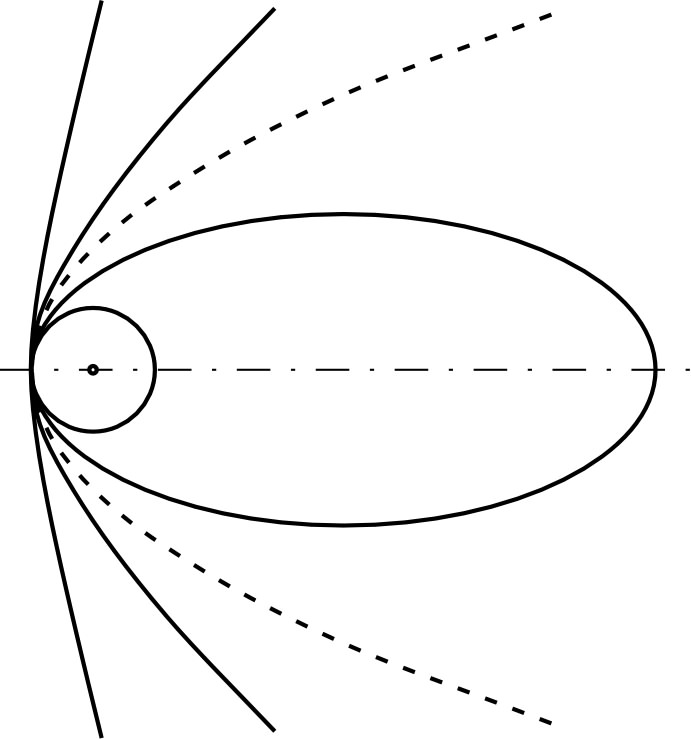
• L’excentricité (positive) caractérise la
forme de la trajectoire :
pour un cercle ;
pour une ellipse ;
pour une parabole ;
pour une hyperbole.
◊ remarque : pour une force répulsive (
), on évite
en se ramenant à l’autre foyer et en décalant
de
(ainsi
) :
.
|
|
|
• Pour le mouvement des planètes, on vérifie les
deux premières lois de Kepler : mouvement elliptique (donc plan)
et selon la loi des aires.
☞ remarque : attention ici à l'utilisation particulière des lettres
,
,
…
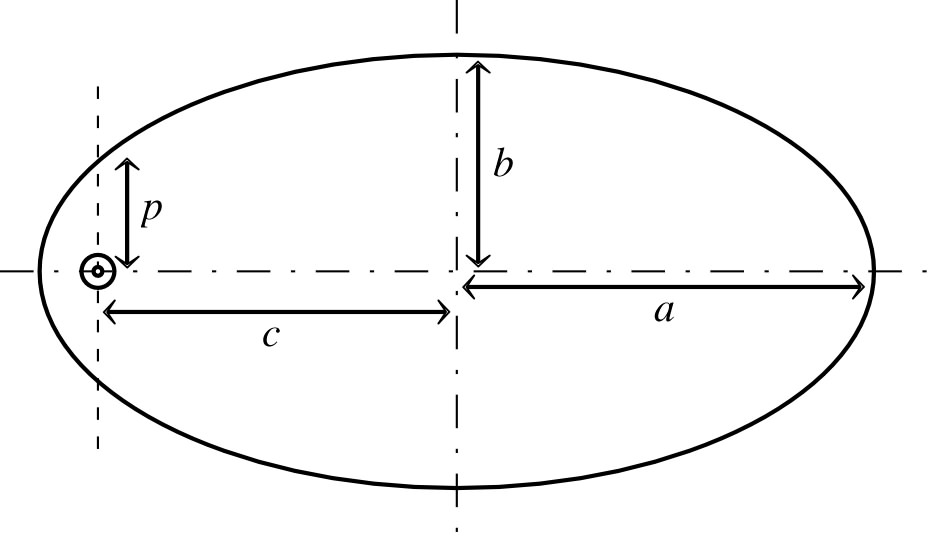
• Pour une ellipse (la somme des distances aux deux foyers est
constante) :
;
;
.
La loi des aires :
donne alors la troisième loi de Kepler, qui relie le
demi-grand-axe de l’ellipse à la période :
.
☞ remarque : la troisième loi de Kepler se
retrouve facilement dans le cas circulaire (
,
ce qui n’est pas trop particulier car
pour la plupart des planètes) :
d’où
.
◊ remarque : ayant calculé
et pour le
mouvement de la Terre, c’est ainsi qu’on a pu en déduire la masse du
Soleil :
.
Aspects énergétiques
• Pour les satellites, la force gravitationnelle dérive de l'énergie
potentielle :
avec
.
L’énergie cinétique est :
donc l’énergie mécanique est :
; ceci correspond à
pour une hyperbole et à
pour une ellipse.
☞ remarque : pour une ellipse
, ce qui se retrouve facilement dans le cas circulaire
:
et
donc
:
et
.
◊ remarque : on retrouve l’équation de la trajectoire d’après
.
Vitesses caractéristiques
Vitesse minimum de satellisation
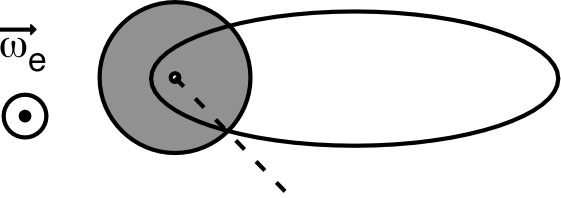
• Avec le centre de la Terre comme foyer, toute trajectoire
elliptique partant du sol retombe sur le sol. En omettant le
frottement sur l'air, un lancer tangentiel depuis le sol donnerait
une trajectoire rasant le sol à chaque pédiode.
La vitesse minimum de satellisation correspondrait à une orbite
circulaire “rasante” de rayon
(avec
) :
et
.
◊ remarque : cette vitesse est définie par rapport à un référentiel
galiléen ; la satellisation est un peu plus facile dans le sens de
rotation de la Terre, avec la vitesse d’entraînement :
à l’équateur.
| ◊ remarque : en pratique on utilise un
lancement légèrement “oblique” dans
galiléen en effectuant un lancement vertical dans
tournant ; cela limite le freinage par l'atmosphère. |
|
|
Orbite géostationnaire
• Pour une orbite plus éloignée, la vitesse sur orbite est plus
faible (sur une orbite circulaire :
), mais l’énergie mécanique y est plus grande donc la vitesse
de lancement doit être plus grande.
Pour l’orbite géostationnaire :
; avec
;
;
.
◊ remarque : la condition géostationnaire donne en fait :
(même
et rayon
plus grand).
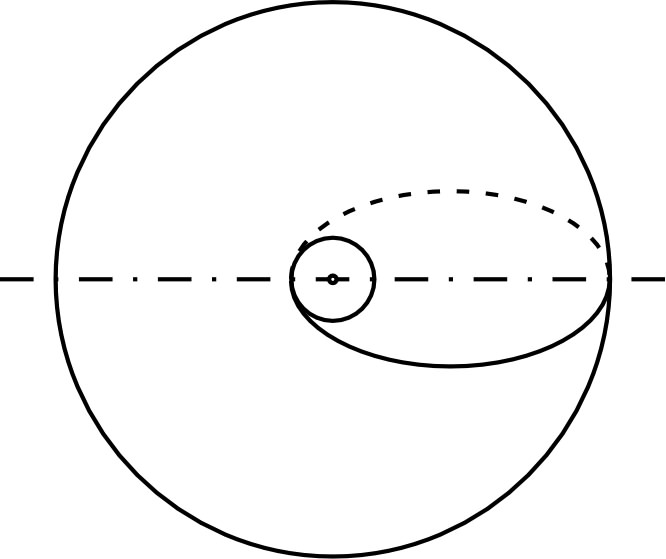
• En supposant partir de l’orbite rasante,
le plus “économique” est de procéder en deux étapes, en
passant par une “orbite de transfert”.
Pour ce transfert :
donc
; partant de
il
faut donc fournir au début du transfert un supplément
:
. |
|
|
Mais avant le transfert :
donc juste au
début du transfert :
et
.
• De même, il faut fournir à la fin du transfert un excédent
d’énergie cinétique :
.
Mais après le transfert :
donc juste à
la fin du transfert :
et
.
◊ remarque :
avant
transfert est supérieure à
après
transfert ; pourtant il faut fournir de l’énergie en début et en fin
de transfert car l’augmentation de l’énergie potentielle conduit à
une forte diminution de vitesse (
).
◊ remarque : d'autres raisonnements sont aussi possibles à l'aide du
moment cinétique.
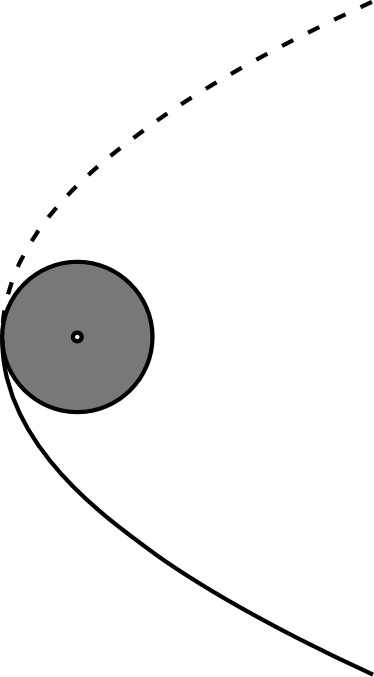
Vitesse minimum de “libération”
• La “libération” de l'attraction
terrestre correspond à un engin spatial pouvant s'éloigner à
l'infini (au contraire des “satellites”), donc au minimum
une trajectoire parabolique (
).
Avec lancement tangent :
(
et
) d'où la “vitesse de libération”
.
On constate que l’intervalle des vitesses de lancement
donnant des orbites elliptiques est assez restreint :
avec
. |
|
|
◊ remarque : la vitesse moyenne des molécules de l’atmosphère
(agitation thermique) est
d’où une probabilité d’échappement plutôt négligeable
.
📖 exercices n° I, II, III, IV, V, VI, VII, VIII, IX et X.