DYNAMIQUE - PLANÈTES ET SATELLITES - corrigé des exercices

A. EXERCICES DE BASE

Décroissance du champ gravitationnel en 1/r2

a.	• Pour un mouvement circulaire, l’accélération est radiale et normale : $\displaystyle a=\frac{v^2}{R'}=ω^2 \: R'=\frac{4 \,π^2 \: R'}{T^2}$ (avec $R'≈60 \,R$ ).

b.	• Si le mouvement circulaire de la Lune est dû à l’attraction terrestre, alors le champ de gravitation terrestre au niveau de la Lune est $g'=a≈2\text{,}72.{10}^{-3} \; \mathrm{m.s^{-2}}$ .

c.	• Ceci donne : $\displaystyle \frac{g'}{g_0} ≈ 2\text{,}78.{10}^{-4}≈{60}^{-2}≈\left(\frac{R'}{R}\right)^{-2}$ d’où une décroissance comme $\displaystyle \frac{1}{r^2}$ .

Trajectoire de la comète de Halley

• D'après la troisième loi de Kepler, le demi-grand-axe

𝒶

et la période

T

vérifient :

\displaystyle \frac{𝒶^3}{T^2} =\frac{𝒢 \:M}{4 \,π^2}

.
◊ remarque : en toute rigueur, l'année ne correspond pas exactement à un tour sur une ellipse car, à cause de différentes perturbations, le grand axe se décale légèrement à chaque tour (il y a un peu plus d'un tour entre deux périhélies successifs) ; en outre, pour des raisons analogues, l'axe des pôles change un peu de direction à chaque révolution autour du Soleil ; ainsi, l'année tropique est définie par le passage au point vernal, quand la direction Soleil-Terre recoupe le plan équatorial (mais la différence est très faible).
• Les calculs sont simplifiés en unités astronomiques puisque pour la Terre :

\displaystyle \frac{𝒶_0^{\:3}}{T_0^{\:2}} =\frac{𝒢 \:M}{4 \,π^2}

avec (par définition) :

a_0=1 \:\mathrm{ua}

T_0=1 \:\mathrm{an}

. Par comparaison :

\displaystyle \frac{𝒶}{𝒶_0} =\left(\frac{T}{T_0} \right)^{2/3}=(76\text{,}03)^{2/3}=17\text{,}95

; par suite :

𝒶=17\text{,}95 \;\mathrm{ua}

.
• En notant

𝒸

la demi-distance entre les foyers de la trajectoire (elliptique), la distance du périhélie est :

𝒶-𝒸=0\text{,}59 \:\mathrm{ua}

; par suite :

𝒸=17\text{,}36 \;\mathrm{ua}

. L'excentricité de l'ellipse est donc :

\displaystyle ℯ=\frac{𝒸}{𝒶}=0\text{,}97

et la distance de l'aphélie est :

𝒶+𝒸=35\text{,}31 \;\mathrm{ua}

Trajectoire d'un satellite terrestre

• D'après la troisième loi de Kepler, le demi-grand-axe

𝒶

et la période

T

vérifient :

\displaystyle \frac{𝒶^3}{T^2} =\frac{𝒢 \:M}{4 \,π^2}

. Par ailleurs pour la Terre :

\displaystyle g_0=\frac{𝒢 \:M}{R^2} =9\text{,}8 \:\mathrm{m.s^{-2}}

donc

\displaystyle 𝒶=\sqrt[3]{\frac{T^2 \: g_0 \: R^2}{4 \,π^2}}=7030 \:\mathrm{km}

• La trajectoire a pour équation :

\displaystyle r=\frac{𝓅}{1+ℯ \;\cos(θ)}

; le périgée est :

\displaystyle r'=\frac{𝓅}{1+ℯ}=h'+R=6750 \:\mathrm{km}

et l’apogée :

\displaystyle r''=\frac{𝓅}{1-ℯ}

; le demi-grand-axe correspond à :

\displaystyle 𝒶=\frac{1}{2} (r'+r'')=\frac{𝓅}{1-ℯ^2}=\frac{r'}{1-ℯ}

d’où on déduit :

\displaystyle ℯ=1-\frac{\,r'}{𝒶}=4.{10}^{-2}

.
◊ remarque : pour ne pas redémontrer, on peut aussi utiliser

\displaystyle ℯ=\frac{𝒸}{𝒶}

avec

𝒸=𝒶-r'

.
• L’apogée

\displaystyle r''=\frac{𝓅}{1-ℯ}=𝒶 .(1+ℯ)=7310 \:\mathrm{km}

correspond à une altitude :

h''=r''-R= 910 \:\mathrm{km}

Énergie de mise sur orbite

• En orbite à basse altitude, on peut considérer que l’énergie potentielle de pesanteur est pratiquement la même qu’à la surface du sol ; l’énergie à fournir correspond alors essentiellement à une variation d’énergie cinétique.
• Le satellite initialement “immobile” au sol a une vitesse

v=R \:ω=465 \:\mathrm{m.s^{-1}}

par rapport à un référentiel géocentrique orienté selon les directions d’étoiles “fixes”. Pour être en orbite à basse altitude, il doit avoir une période de révolution

T

telle que :

\displaystyle \frac{R^3}{T^2} =\frac{𝒢 \:M}{4 \,π^2}

avec

\displaystyle g_0=\frac{𝒢 \:M}{R^2} =9\text{,}8 \:\mathrm{m.s^{-2}}

et une vitesse :

v'=R \:ω'=\sqrt{R \:g_0}=7920 \:\mathrm{m.s^{-1}}

.
• Pour mettre le satellite en orbite dans le sens de rotation de la Terre, il suffit de faire passer son énergie cinétique de

E_c=\frac{1}{2} m \:v^2

E'_c=\frac{1}{2} m \:{v'}^2

d’où une énergie fournie

E'=E'_c-E_c=2\text{,}50.{10}^9 \:\mathrm{J}

.
• Par contre, pour mettre le satellite en orbite dans le sens contraire de la rotation de la Terre, il faut compenser son mouvement initial pour le faire tourner dans l’autre sens (travail résistant non récupérable). Il faut donc fournir

E''=E_c+E'_c=2\text{,}52.{10}^9 \:\mathrm{J}

.
• L’écart relatif est ainsi :

\displaystyle \frac{ΔE}{E}≈\frac{2 \,E_c}{E'_c}=\frac{2 \,v^2}{{v'}^2} ≈7.{10}^{-3}

Satellite géostationnaire et précision du lancement

• Sur une orbite géostationnaire, la vitesse de angulaire est la même que celle de la Terre sur elle-même :

\displaystyle ω=\frac{2π}{T}

avec

T=1 \:\mathrm{jour}≈86400 \:\mathrm{s}

(en fait il s'agit d'un jour sidéral et non d'un jour solaire, mais la différence est négligeable en première approximation), soit :

ω=7\text{,}3.{10}^{-5} \:\mathrm{rad.s^{-1}}

.
• Sur la trajectoire géostationnaire, circulaire, l'accélération centripète est :

\displaystyle a_r=\frac{v_0^{\:2}}{r_0} =\frac{𝒢 \:M}{r_0^{\:2}}

et donc :

\displaystyle ω^2=\left(\frac{v_0}{r_0} \right)^2=\frac{𝒢 \:M}{r_0^{\:3}}

(ceci équivaut à la troisième loi de Kepler). Par suite :

\displaystyle r_0=\sqrt[3]{\frac{𝒢 \:M}{ω^2}}=\sqrt[3]{\frac{g \:R^2}{ω^2}}

en utilisant

\displaystyle g=\frac{𝒢 \:M}{R^2}

où

R≈6400 \:\mathrm{km}

est le rayon terrestre ; ainsi :

r_0≈42300 \:\mathrm{km}

.
• La vitesse du satellite est par suite :

v_0=r_0 \: ω=3080 \:\mathrm{m.s^{-1}}

.
• L'énergie cinétique est :

\displaystyle E_{c0}=\frac{1}{2} m \:v_0^{\:2}=\frac{𝒢 \:M \:m}{2 \,r_0}

; l'énergie potentielle est :

\displaystyle E_{p0}=-\frac{𝒢 \:M \:m}{r_0}

; l'énergie mécanique est :

\displaystyle E_{m0}=-\frac{𝒢 \:M \:m}{2 \,r_0}=-E_{c0}

• On peut étudier d'une façon plus générale l'énergie cinétique en fonction des caractéristiques de la trajectoire ; on peut en particulier utiliser le résultat général démontré en cours pour les trajectoires non circulaires :

\displaystyle E_m=-\frac{𝒢 \:M \:m}{2 \:𝒶}

(ceci se démontre en considérant la loi des aires et la première formule de Binet, avec l'expression de la trajectoire elliptique en coordonnées polaires).
• On peut écrire :

\displaystyle E_{m0}=\frac{1}{2} m \:v_0^{\:2}-\frac{𝒢 \:M \:m}{r_0}

et dans le cas général, au point de lancement (

r=r_0

) :

\displaystyle E_m=\frac{1}{2} m \:v^2-\frac{𝒢 \:M \:m}{r_0}

. Mais l'incertitude sur la vitesse :

\displaystyle v=v_0+Δv=v_0 .\left(1+\frac{Δv}{v_0} \right)

provoque une incertitude sur l'énergie :

\displaystyle E_m=\frac{1}{2} m \:v_0^{\:2}.\left(1+\frac{Δv}{v_0} \right)^2-\frac{𝒢 \:M \:m}{r_0}

.
• Pour une incertitude

Δv

faible :

E_m≈E_{m0}+m \:v_0 \; Δv

; mais par ailleurs:

\displaystyle m \:v_0^{\:2}=\frac{𝒢 \:M \:m}{r_0} =-2 \,E_{m0}

donc :

\displaystyle E_m≈E_{m0} .\left(1-2 \,\frac{Δv}{v_0} \right)

.
• De :

\displaystyle E_m=-\frac{𝒢 \:M \:m}{2 \,𝒶}

on déduit alors :

\displaystyle 𝒶=-\frac{𝒢 \:M \:m}{2 \,E_m}≈-\frac{𝒢 \:M \:m}{2 \,E_{m0}} \:\left(1+2 \,\frac{Δv}{v_0} \right)≈r_0 .\left(1+2 \,\frac{Δv}{v_0} \right)

.
• Le lancement, à l'apogée de la trajectoire de la fusée, correspond à une vitesse radiale nulle, donc à l'apogée ou au périgée de l'orbite du satellite. L'équation de la trajectoire :

\displaystyle \frac{1}{r}=\frac{1}{𝓅} \: [1+ℯ \;\cos(θ) ]

indique que le lancement correspond à :

\displaystyle r_0=\frac{𝓅}{1±ℯ}=𝒶 .(1±ℯ)

suivant le cas (signe de

Δv

). Par suite, puisque l'excentricité est positive :

\displaystyle ℯ=\left|1-\frac{r_0}{𝒶}\right|=2 \, \frac{Δv}{v_0}

• De

\displaystyle T=2π \,\sqrt{\frac{𝒶^3}{𝒢 \:M}}

on déduit :

\displaystyle \frac{ΔT}{T}=\frac{3}{2} \frac{Δ𝒶}{𝒶}

; mais par ailleurs

\displaystyle \frac{Δ𝒶}{𝒶}=1-\frac{r_0}{𝒶}=2 \, \frac{Δv}{v_0}

donc :

\displaystyle \frac{ΔT}{T}=3 \, \frac{Δv}{v_0}

. Une incertitude maximum de un tour par an correspond à

\displaystyle \frac{|ΔT|}{T}≈\frac{1}{365}

donc :

\displaystyle \frac{|Δv|}{v_0} ≈\frac{1}{3} \frac{|ΔT|}{T}≈0\text{,}9.{10}^{-3}

Masse d'une galaxie

• D’après la troisième loi de Kepler :

\displaystyle \frac{r^3}{T^2} =\frac{𝒢 \:M}{4 \,π^2}

avec

\displaystyle T=\frac{2π \:r}{v}

donc :

\displaystyle M=\frac{r \:v^2}{𝒢}=2\text{,}8.{10}^{41} \: \mathrm{kg}

. Si on compare cette masse à celle du Soleil, en supposant que celui-ci est une étoile “moyenne”, on peut penser que l’ordre de grandeur du nombre d’étoiles dans la galaxie est :

\displaystyle N≈\frac{M}{m}≈140 \:\mathrm{milliards}

Variante de la méthode de Binet

• La conservation du moment cinétique impose un mouvement plan ; en coordonnées polaires dans le plan du mouvement :

\overset{→}{v}=\dot{r} \; \overset{→}{u}_r+r \:\dot{θ} \; \overset{→}{u}_θ

.
• En considérant

\displaystyle \dot{r}=\frac{dr}{d𝓊} \frac{d𝓊}{dθ} \, \dot{θ}

avec

\dot{θ}=C \:𝓊^2

(loi des aires), on obtient

\displaystyle\dot{r}=-C \, \frac{d𝓊}{dθ}

r\: \dot{θ}=C \:𝓊

. La première formule de Binet est donc :

\displaystyle \overset{→}{v}=C .\left(- \frac{d𝓊}{dθ} \: \overset{→}{u}_r+𝓊 \;\overset{→}{u}_θ \right)

.
• On en déduit :

\displaystyle E_c=\frac{1}{2} m \:v^2=\frac{1}{2} m \:C^2 \,\left( \left(\frac{d𝓊}{dθ}\right)^2+𝓊^2 \right)

• L'énergie mécanique peut s'écrire :

E_m=E_c+E_p

avec

E_p=-𝒢 \:M \:m \:𝓊

.
• La conservation de l'énergie mécanique donne :

\displaystyle \dot{E}_m=0=m \:C^2 \:\left(\frac{d𝓊}{dθ} \frac{d^2 𝓊}{{dθ}^2} +𝓊 \:\frac{d𝓊}{dθ}\right) \: \dot{θ}=-𝒢 \:M \:m \,\frac{d𝓊}{dθ} \, θ ̇

.
• Dans le cas général (

r

θ

non constants) le mouvement correspond à

m \:C^2 \, \frac{d𝓊}{dθ} \: \dot{θ}≠0

et donc :

\displaystyle \frac{d^2 𝓊}{{dθ}^2} +𝓊-\frac{𝒢 \:M}{C^2} =0

.
• Les solutions sont de la forme :

\displaystyle 𝓊=\frac{1}{r}=\frac{𝒢 \:M}{C^2} \, [1+ℯ \;\cos(θ) ]

en prenant comme origine des angles la direction du point le plus proche de l'astre.

Vecteur excentricité

• La relation fondamentale de la dynamique peut s'écrire (en simplifiant par

m

) :

\displaystyle \frac{d\overset{→}{v}}{dt}=-\frac{𝒢 \:M}{r^2} \, \overset{→}{u}_r

.
• La loi des aires correspond à

C=r^2 \: \dot{θ}

donc :

\displaystyle \frac{d\overset{→}{v}}{dt}=-\frac{𝒢 \:M}{C}\, \dot{θ} \; \overset{→}{u}_r

.
• D'après la relation

\dot{\overset{→}{u}}_θ=-\dot{θ} \; \overset{→}{u}_r

on en déduit :

\displaystyle \frac{d\overset{→}{v}}{dt}=\frac{𝒢 \:M}{C} \, \dot{\overset{→}{u}}_θ

;

\displaystyle \overset{→}{v}=\frac{𝒢 \:M}{C} \, \left(\overset{→}{u}_θ+\overset{→}{ℯ} \right)

où

\overset{→}{ℯ}

est une constante d'intégration.

2.	• La composante orthoradiale de la vitesse est : $\displaystyle r\: \dot{θ}=\overset{→}{v}⋅\overset{→}{u}_θ=\frac{𝒢 \:M}{C} \, \left(1+\overset{→}{ℯ}⋅\overset{→}{u}_θ \right)$ .

3.	• Compte tenu de la loi des aires : $\displaystyle \frac{1}{r}=\frac{r \:\dot{θ}}{C}=\frac{𝒢 \:M}{C^2} \, [1+ℯ \;\cos(θ) ]$ en prenant comme origine des angles la direction du vecteur excentricité.

Invariant de Laplace-Runge-Lenz

1.a.	• En dérivant la propriété $\overset{→}{r}^2=r^2$ on obtient : $2\, \overset{→}{r}⋅\dot{\overset{→}{r}}=2 \,r\: \dot{r}$ .

1.b.	• On peut considérer : $\displaystyle \dot{\overset{→}{u}}_r=\frac{d}{dt} \left(\frac{\,\overset{→}{r}}{r}\right)=\frac{\dot{\overset{→}{r}} \: r-\overset{→}{r} \: \dot{r}}{r^2} =\frac{\dot{\overset{→}{r}} \: r^2-\overset{→}{r} \: r \:\dot{r}}{r^3} =\frac{(\overset{→}{r}⋅\overset{→}{r} \,) \: \dot{\overset{→}{r}}-(\overset{→}{r}⋅\dot{\overset{→}{r}} \,) \: \overset{→}{r}}{r^3} =\frac{(\overset{→}{r} × \dot{\overset{→}{r}} \,) × \overset{→}{r}}{r^3} =\frac{\overset{→}{C} × \overset{→}{r}}{r^3 }$ .

2.a.	• La relation fondamentale de la dynamique peut s'écrire : $\displaystyle \overset{→}{a}=\frac{\overset{→}{F}}{m}=-𝒢 \:M \,\frac{\overset{→}{r}}{r^3}$ . • Par comparaison avec la relation précédente, on en déduit : $\displaystyle \overset{→}{C} × \overset{→}{a}=-𝒢 \:M\, \frac{\overset{→}{C} × \overset{→}{r}}{r^3} =-𝒢 \:M \;\dot{\overset{→}{u}}_r$ .

2.b.	• Puisque $\overset{→}{C}$ est constant : $\displaystyle \overset{→}{C} × \overset{→}{a}=\frac{d}{dt} \left(\overset{→}{C} × \overset{→}{v} \right)$ . On en déduit : $\displaystyle \frac{d}{dt} \left(\overset{→}{v} × \overset{→}{C}-𝒢 \:M \;\overset{→}{u}_r \right)=\overset{→}{0}$ . ◊ remarque : le vecteur $\overset{→}{R}$ n'est pas indépendant du vecteur excentricité.

• En prenant l'orientation de

\overset{→}{R}

comme origine des angles, on peut écrire :

\overset{→}{R}⋅\overset{→}{u}_r=R \; \cos(θ)

.
• Mais par ailleurs :

\displaystyle \overset{→}{R}⋅\overset{→}{u}_r=\left(\overset{→}{v} × \overset{→}{C} \,\right)⋅\overset{→}{u}_r-𝒢 \:M=\left(\overset{→}{u}_r × \overset{→}{v} \right)⋅\overset{→}{C}-𝒢 \:M=\frac{C^2}{r}-𝒢 \:M

.
• Par comparaison, on obtient :

\displaystyle \frac{1}{r}=\frac{𝒢 \:M}{C^2} \, \left[1+\frac{R}{𝒢 \:M} \: \cos(θ) \right]

où on peut poser

\displaystyle ℯ=\frac{R}{𝒢 \:M}

Caractéristiques d'une orbite elliptique

1.a.	• L'énergie mécanique est initialement $\displaystyle E_m=-\frac{𝒢 \:M \:m}{2 \,R}$ (avec un demi grand-axe $𝒶=R$ ). La nouvelle valeur (divisée par deux) correspond à un demi grand-axe $𝒶'=2 \,R$ . ◊ remarque : pour un satellite l'énergie mécanique est négative, donc la diviser par deux correspond à une augmentation.

1.b.	• La trajectoire proposée est incohérente car elle recoupe le cercle : il existerait des points de la nouvelle trajectoire plus proches que la position $P$ initiale. Or, le demi grand-axe ayant augmenté (presque) sans déplacement, le centre de la Terre est forcément le foyer le plus proche du point de changement d'orbite, c'est-à-dire que ce dernier est le périgée ; il est incohérent d'envisager une trajectoire ayant des points plus proches.

2.a.	• La poussée tangentielle de courte durée ne modifie pas la distance à la Terre, donc seule l'énergie cinétique est modifiée : $\displaystyle E'_c=E'_m-E'_p=E'_m-E_p =-\frac{𝒢 \:M \:m}{4 \,R}+\frac{𝒢 \:M \:m}{R}=\frac{3}{2} E_c$ . • On en déduit la proportion des vitesses : $v'=\sqrt{\frac{3}{2}} \: v$ .

2.b.	• Le moment cinétique est relié à constante $C$ de la loi des aires et à la vitesse aréolaire $\displaystyle \dot{S}=\frac{π \,𝒶 \,𝒷}{T}$ ; ainsi : $\displaystyle L= m \:C=2 \,m \:\dot{S}=m \,\frac{2π \,𝒶 \,𝒷}{T}$ . • La troisième loi de Kepler donne par ailleurs : $\displaystyle \frac{𝒶^3}{T^2} =\frac{𝒢 \:M}{4 \,π^2}$ ; par comparaison : $\displaystyle L=m \:𝒷 \,\sqrt{\frac{𝒢 \:M}{𝒶}}$ .

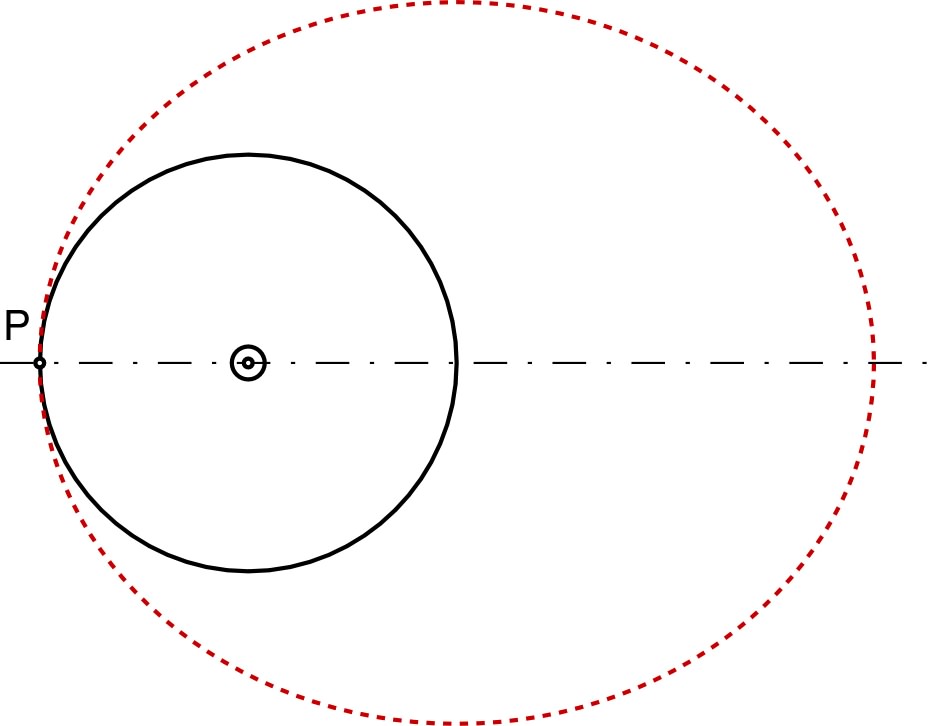
2.c.	• Le moment cinétique (constant sur la trajectoire) peut s'écrire : $L=R \:v$ avant le changement d'orbite, puis $L'=R \:v'=\sqrt{\frac{3}{2}} \: L$ après. Par comparaison : $\displaystyle \frac{𝒷'}{𝒷}=\frac{L'}{L} \sqrt{\frac{𝒶'}{R}}= \sqrt{3}$ . • On en déduit l'allure de la trajectoire :

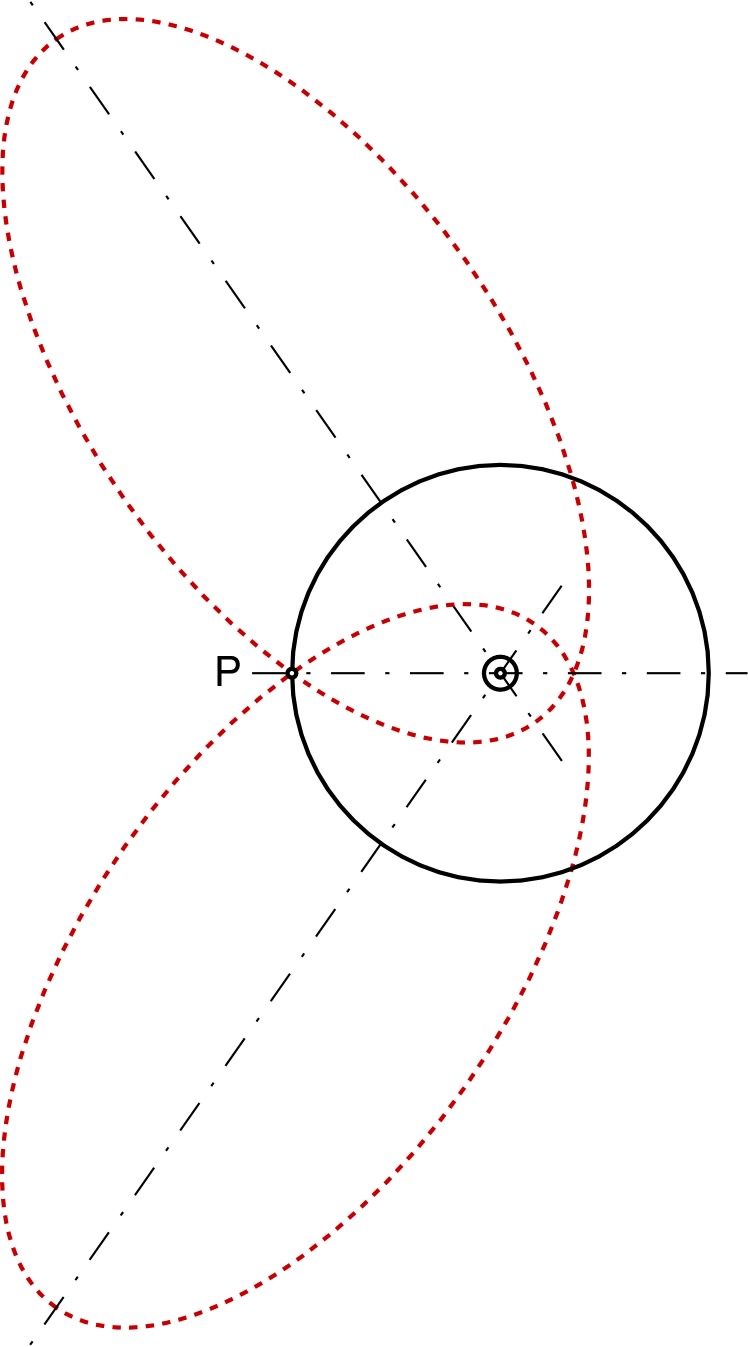
3.a.

• Pour modifier la trajectoire d'une façon qui ne modifie pas le moment cinétique, il est nécessaire et suffisant d'exercer une force centrale. D'après (2.b), on peut préciser que le moment cinétique non modifié impose que

𝒷

varie proportionnellement à

\sqrt{𝒶}

• On suppose que la durée est très courte (limite idéalisée utilisée ici pour simplifier certains calculs), de telle façon que la force ne modifie pratiquement pas la distance à l'astre (donc l'énergie potentielle) ni la composante tangentielle de la vitesse (pour ne pas changer

L

). Cela ne fait que changer la direction de la vitesse en ajoutant une composante radiale ; la vitesse et l'énergie cinétique augmentent au second ordre ; ceci augmente l'énergie mécanique, donc aussi le demi grand-axe (et donc aussi

𝒷

).
◊ remarque : cela implique une variation d'orientation des axes vu la conclusion de la question (1.b) ; d'après les relations de l'ellipse, le paramètre

\displaystyle 𝓅=\frac{𝒷^2}{𝒶}=R

n'est pas modifié, mais l'excentricité (qui était nulle) augmente :

\displaystyle ℯ'=\sqrt{1-\frac{{𝒷'}^2}{{𝒶'}^2}}=\sqrt{1-\frac{R}{𝒶'}}>0

; l'équation de la trajectoire impose alors :

\displaystyle \frac{1}{R}=\frac{1}{R} \, [1+ℯ' \;\cos(θ) ]

donc

θ=±\frac{π}{2}

dynSatellites_cor_Im/dynSatellites_cor_Im2.jpg

3.b.	• On envisage une première action donnant une valeur intermédiaire $𝒶''=λ \:R$ ; on obtient ainsi : $\displaystyle E''_c=E''_m-E_p=-\frac{𝒢 \:M \:m}{2 \,λ \:R}+\frac{𝒢 \:M \:m}{R}=\frac{2 \,λ-1}{λ} \, E_c$ ; $\displaystyle \frac{L''}{L}=\frac{v''}{v}=\sqrt{\frac{2 \,λ-1}{λ}}$ ; $\displaystyle \frac{𝒷''}{𝒷}=\frac{L''}{L} \sqrt{\frac{𝒶''}{R}}=\sqrt{2\, λ-1}$ . • Puis on applique la seconde action telle que $L'=L''$ et $\displaystyle \frac{𝒷'}{𝒷''}=\frac{1}{\sqrt{2 \,λ-1}}$ (pour rétablir $𝒷'=𝒷=R$ ) ; ceci impose : $\displaystyle \frac{𝒶'}{𝒶''}=\frac{λ}{2 \,λ-1}$ . • Pour obtenir $\displaystyle 𝒶'=\frac{λ}{2 \,λ-1} \, R = 2 \,R$ il est nécessaire et suffisant de choisir $λ=\frac{2}{3}$ (correspondant à un freinage, le bilan énergétique est un gaspillage désastreux !).

3.c.	• La première action correspond à une force parallèle à la vitesse et de sens contraire ; la seconde action correspond à une force perpendiculaire à la vitesse et peut être orientée vers la Terre ou du côté opposé (les deux sens augmentent le demi grand-axe). • La combinaison des deux donne une force orientée entre les deux (avec une coordonnée positive ou négative selon $\overset{→}{u}_r$ et une coordonnée négative selon $\overset{→}{u}_θ$ ). ◊ remarque : on peut préciser l'orientation des axes, selon la question (1.b) ; les relations de l'ellipse donnent $\displaystyle 𝓅'=\frac{{𝒷'}^2}{𝒶'}=\frac{R}{2}$ et $\displaystyle ℯ'=\sqrt{1-\frac{{𝒷'}^2}{{𝒶'}^2}}=\frac{\sqrt{3}}{2}$ ; l'équation de la trajectoire impose alors : $\displaystyle \frac{1}{R}=\frac{2}{R} \, [1+ℯ' \;\cos(θ) ]$ et ainsi : $θ=±\arccos⁡\left(-\frac{1}{\sqrt{3}}\right)=± 125 \:°$ .

dynSatellites_cor_Im/dynSatellites_cor_Im3.jpg

B. EXERCICES D’APPROFONDISSEMENT

Aplatissement du soleil et avance du périhélie

• Pour un potentiel gravitationnel de la forme

\displaystyle 𝒱(r)≈-\frac{𝒢 \:M}{r}-\frac{β}{r^3}

le champ gravitationnel est (dans le plan équatorial) :

\displaystyle \overset{→}{g}=-\overset{→}{∇}𝒱=\left(-\frac{𝒢 \:M}{r^2} -\frac{3 \,β}{r^4} \right) \; \overset{→}{u}_r

.
• D'après la seconde formule de Binet :

\displaystyle m \:\overset{→}{a}=m \:\ddot{r} \;\overset{→}{u}_r=-m \:C^2 \: 𝓊^2 \:\left(\frac{d^2 𝓊}{{dθ}^2} +𝓊\right) \; \overset{→}{u}_r=m \:\overset{→}{g}

, donc l'équation différentielle du mouvement peut s’écrire :

\displaystyle \frac{d^2 𝓊}{{dθ}^2} +𝓊=\frac{𝒢 \:M}{C^2} +\frac{3 \,β}{C^2} \, 𝓊^2

• Si on cherche une solution approchée sous la forme :

\displaystyle 𝓊=\frac{1}{r}=\frac{1}{𝓅} \, [1+ℯ \;\cos(γ \:θ) ]

l'équation différentielle du mouvement correspond à :

\displaystyle \frac{1}{𝓅}+(1-γ^2 ) \, \frac{ℯ}{𝓅} \: \cos(γ \:θ)≈\frac{𝒢 \:M+\frac{3 \,β}{𝓅^2}}{C^2} +\frac{6 \,ℯ \:β}{𝓅^2 \: C^2} \: \cos⁡(γ \:θ)

(en négligeant le terme en

ℯ^2

).
• On obtient par identification :

\displaystyle \frac{1}{𝓅}≈\frac{𝒢 \:M}{C^2} \, \left(1+3 β \,\frac{𝒢 \:M}{C^4} \right)

\displaystyle (1-γ^2 )≈\frac{6 \,β}{𝓅 \:C^2}≈6 \,β \, \frac{𝒢 \:M}{C^4}

d'où on déduit :

\displaystyle γ≈1-3 \,β \, \frac{𝒢 \:M}{C^4}

(donc

≈1

dans la limite où le terme correctif est petit) et

\displaystyle \frac{1}{𝓅}≈\frac{𝒢 \:M}{γ \:C^2}

.
• Ceci correspond à un mouvement approximativement elliptique, mais tel qu'à chaque période du cosinus (pseudo-période du mouvement) correspond une variation angulaire telle que :

Δ(γ \:θ)=2π

, c'est-à-dire :

\displaystyle ∆θ=\frac{2π}{γ}≈2π \:\left(1+3 \,β \,\frac{𝒢 \:M}{C^4} \right)

.
• Si on néglige le terme en

ℯ^2

(comme dans l'approximation précédente) l'avance du périhélie est :

$\displaystyle δθ=∆θ-2π=6π \,β \, \frac{𝒢 \:M}{C^4} =\frac{6π \,𝒢^2 \: M^2 \: ε \:R_e^{\:2}}{5 \,C^4}=\frac{6π \:ε \:R_e^{\:2}}{5 \,𝓅^2}=\frac{6π \:ε \:R_e^{\:2}}{5\, 𝒶^2 \: (1-ℯ^2 \,)^2}≈\frac{6π \,ε \:R_e^{\:2}}{5 \,𝒶^2}$ .

3.	• On obtient pour mercure : $δθ=3\text{,}0.{10}^{-8} \:\mathrm{rad}$ pour une pseudo-période. Or, il y a $415 \:\mathrm{périodes}$ de $88 \:\mathrm{jours}$ dans un siècle ; donc ceci correspond à une avance du périhélie : $δθ=1\text{,}2.{10}^{-5} \: \mathrm{rad}=2\text{,}5 \:''$ par siècle.

Avance relativiste du périhélie

• Si on cherche une solution approchée sous la forme :

\displaystyle 𝓊=\frac{1}{r}=\frac{1}{𝓅} \, [1+ℯ \;\cos(γ \:θ) ]

l'équation différentielle du mouvement correspond à :

\displaystyle \frac{1}{𝓅}+(1-γ^2 ) \, \frac{ℯ}{𝓅} \: \cos(γ \:θ)≈\frac{𝒢 \:M}{C^2} +\frac{3 \,𝒢 \:M}{c_0^{\:2} \:𝓅^2} +\frac{6 \,ℯ \:𝒢 \:M}{c_0^{\:2} \:𝓅^2} \: \cos⁡(γ \:θ)

(en négligeant le terme en

ℯ^2

).
• On obtient par identification :

\displaystyle \frac{1}{𝓅}≈\frac{𝒢 \:M}{C^2} \, \left(1+3 \,\left(\frac{𝒢 \:M}{C \:c_0}\right)^2 \right)

\displaystyle (1-γ^2 )≈\frac{6 \,𝒢 \:M}{c_0^{\:2} \: 𝓅}≈6\,\left(\frac{𝒢 \:M}{C \:c_0}\right)^2

d'où on déduit :

\displaystyle γ≈1-3\,\left(\frac{𝒢 \:M}{C \:c_0}\right)^2

(donc

≈1

dans la limite où le terme correctif est petit) et

\displaystyle \frac{1}{𝓅}≈\frac{𝒢 \:M}{γ \:C^2}

.
• Ceci correspond à un mouvement approximativement elliptique, mais tel qu'à chaque période du cosinus (pseudo-période du mouvement) correspond une variation angulaire telle que :

Δ(γ \:θ)=2π

, c'est-à-dire :

\displaystyle ∆θ=\frac{2π}{γ}≈2π \,\left(1+3\,\left(\frac{𝒢 \:M}{C \:c_0}\right)^2 \right)

. L'avance du périhélie est :

\displaystyle δθ=∆θ-2π=6π \,\left(\frac{𝒢 \:M}{C \:c_0}\right)^2

.
• Pour une trajectoire elliptique, on établit les relations :

\displaystyle 𝓅 \:𝒶 .(1-ℯ^2 \, )=\frac{C^2}{𝒢 \:M}

;

\displaystyle ℯ=\frac{𝒸}{𝒶}

;

𝒷^2=𝓅 \:𝒶

;

\displaystyle C=\frac{2π \:𝒶 \:𝒷}{T}

; on en déduit :

\displaystyle δθ=\frac{24 \,π^3 \: 𝒶^2}{T^2 \: c_0^{\:2} \: (1-ℯ^2 \, )}≈\frac{24 \,π^3 \: 𝒶^2}{T^2 \: c_0^{\:2}}

si on néglige le terme en

ℯ^2

comme cela a été fait dans l'approximation précédente.

2.	• On obtient pour mercure : $δθ=5\text{,}0.{10}^{-7} \: \mathrm{rad}$ pour une pseudo-période. Or, il y a $415 \:\mathrm{périodes}$ de $88 \:\mathrm{jours}$ dans un siècle ; donc ceci correspond à une avance du périhélie : $δθ≈2\text{,}0.{10}^{-4} \: \mathrm{rad}=43 \:''$ par siècle.