M. IX - DYNAMIQUE ; SYSTÈMES DE POINTS

Éléments cinétiques d’un système de points

• Le centre d’inertie

G

(ou barycentre des masses) d’un système de points

\{M_i\}

peut être défini par :

( ∑ m_i ) \; \overset{⟶}{OG}=∑\left(m_i \; \overset{⟶}{OM}_i \right)

ou aussi :

∑ \left(m_i \; \overset{⟶}{GM}_i \right) =\overset{→}{0}

On en déduit par dérivation la quantité de mouvement totale du système, aussi appelée “résultante cinétique” :

\overset{→}{p}=∑ \,\overset{→}{p}_i =∑ \left(m_i \; \overset{→}{v}_i \right) =( ∑ m_i ) \: \overset{→}{v}_G

. Le point

G

est donc un bon représentant de cette quantité.

• La situation est un peu différente pour les rotations : le moment cinétique total

\displaystyle \overset{→}{L}_O=∑ \,\overset{→}{L}_{iO}=∑ \left( \overset{⟶}{OM}_i × \overset{→}{p}_i \right)

est généralement différent de

\overset{⟶}{OG} × \overset{→}{p}

Par contre, si tous les

\overset{→}{v}_i

sont égaux (

\overset{→}{v}_i=\overset{→}{v}_G

), alors on peut écrire :

$\overset{→}{L}_O={\displaystyle ∑} \left( \overset{⟶}{OM}_i × m_i \; \overset{→}{v}_i \right) ={\displaystyle ∑} \left(m_i \; \overset{⟶}{OM}_i \right) × \overset{→}{v}_G=(∑ m_i ) \: \overset{⟶}{OG} × \overset{→}{v}_G=\overset{⟶}{OG} × \overset{→}{p}$ ;

la condition pour qu’un système puisse être représenté par un point matériel est en fait que tous les

\overset{→}{v}_i

soient égaux : ni déformation, ni rotation, ce qui correspond à un solide en translation.

• Le changement de centre de référence des moments correspond à :

$\overset{→}{L}_{O\text{’}}={\displaystyle ∑} \left( \overset{⟶}{O\text{’}M}_i × \overset{→}{p}_i \right) =\overset{⟶}{O\text{’}O} × ∑ \,\overset{→}{p}_i +{\displaystyle ∑} \left( \overset{⟶}{OM}_i × \overset{→}{p}_i \right) =\overset{⟶}{O\text{’}O} × \overset{→}{p}+\overset{→}{L}_{O}$ .

◊ remarque : un système peut pour cet aspect être traité comme un point matériel si

\overset{→}{L}_G=\overset{→}{0}

(absence de rotation globale, éventuellement par compensation) ; ceci conduit alors en effet à

\overset{→}{L}_O=\overset{⟶}{OG} × \overset{→}{p}+\overset{→}{L}_G=\overset{⟶}{OG} × \overset{→}{p}

• De même pour l’énergie cinétique :

E_c=∑ \,E_{ci} ={\displaystyle ∑} \left(\frac{1}{2} m_i \: v_i^{\:2} \right) ={\displaystyle ∑ \frac{p_i^{\:2}}{2 \,m_i}}

est généralement différente de

\frac{1}{2} \left( ∑ m_i \right) \: v_G^{\:2}={\displaystyle \frac{p^2}{2 \,∑ m_i}}

Par contre, si tous les

\overset{→}{v}_i

sont égaux (

\overset{→}{v}_i=\overset{→}{v}_G

), alors on peut écrire :

$E_c={\displaystyle ∑} \left(\frac{1}{2} m_i \: v_i^{\:2} \right) =\frac{1}{2}\, ( ∑ m_i ) \, v_G^{\:2}$ .

📖 exercices n° I et II.

Éléments résultants des forces

• Puisque les forces intérieures se compensent deux à deux (actions réciproques), la “résultante dynamique” (somme des forces exercées sur le système) est égale à la somme des forces “extérieures” :

\overset{→}{F}=∑ \,\overset{→}{F}_i =∑_{\text{ext}} \overset{→}{F}_i

• La situation est analogue mais un peu moins évidente pour le “moment dynamique” (somme des moments des forces exercées sur le système) ; en effet, deux forces opposées n’ont pas forcément des moments opposés (ils peuvent même être égaux) : tout dépend des droites d’action.

Si les

M_i

sont des points matériels (en particulier sans effet magnétique) alors les actions réciproques intérieures opposées ont de plus même droite d’action, parallèle à leur direction commune ; par suite leurs moments sont opposés :

$\overset{→}{ℳ}_{(2→1)O}+\overset{→}{ℳ}_{(1→2)O}=\overset{⟶}{OM}_1 × \overset{→}{F}_{2→1}+\overset{⟶}{OM}_2 × \overset{→}{F}_{1→2}=\overset{⟶}{M_1 M}{}_2 × \overset{→}{F}_{1→2}=\overset{→}{0}$ .

On obtient alors :

\overset{→}{ℳ}_O=∑ \,\overset{→}{ℳ}_{iO} =∑_{\text{ext}} \overset{→}{ℳ}_{iO}

• Le changement de point de référence correspond à :

$\overset{→}{ℳ}_{O\text{’}}={\displaystyle ∑} \left( \overset{⟶}{O\text{’}M}_i × \overset{→}{F}_i \right) =\overset{⟶}{O\text{’}O} × ∑ \,\overset{→}{F}_i +{\displaystyle ∑} \left( \overset{⟶}{OM}_i × \overset{→}{F}_i \right) =\overset{⟶}{O\text{’}O} × \overset{→}{F}+\overset{→}{ℳ}_O$ .

Théorèmes de la dynamique des systèmes

• Dans un référentiel galiléen, le principe fondamental de la dynamique peut se généraliser en un “théorème de la résultante cinétique” (ou “théorème du centre d’inertie”) :

{\displaystyle \frac{d\overset{→}{p}}{dt}}=∑ \,\overset{→}{F}_i =∑_{\text{ext}} \overset{→}{F}_i =\overset{→}{F}

• D’une façon analogue, dans un référentiel galiléen, le principe fondamental de la dynamique de rotation se généralise en un “théorème du moment cinétique” : par rapport à un point

O

fixe :

{\displaystyle \frac{d\overset{→}{L}_O}{dt}}=∑ \,\overset{→}{ℳ}_{iO} =∑_{\text{ext}} \overset{→}{ℳ}_{iO} =\overset{→}{ℳ}_O

◊ remarque : plus généralement pour

O

mobile

{\displaystyle \frac{d\overset{→}{L}_O}{dt}}=∑ \,\overset{→}{ℳ}_{iO} -\overset{→}{v}_O × ∑ \,\overset{→}{p}_i

Mais, cas particulier “exceptionnel”, le théorème se généralise par rapport au barycentre

G

(mobile) :

{\displaystyle \frac{d\overset{→}{L}_G}{dt}}=∑ \,\overset{→}{ℳ}_{iG} -\overset{→}{v}_G × \overset{→}{p}=∑_{\text{ext}} \overset{→}{ℳ}_{iG} =\overset{→}{ℳ}_{G}

• La situation est analogue pour l’énergie cinétique (dans un référentiel galiléen) :

dE_c=∑ \,δW_i

; mais il n’y a en général pas compensation des travaux des forces intérieures.

Pour un système sans déformation, si les

M_i

sont des points matériels, alors les actions réciproques intérieures (opposées) ont une même droite d’action selon leur direction commune ; donc leurs travaux sont opposés :

$δW_1+δW_2= \overset{→}{F}_{2→1}⋅d\overset{⟶}{OM}_1 +\overset{→}{F}_{1→2}⋅d\overset{⟶}{OM}_2 =\overset{→}{F}_{1→2}⋅d\overset{⟶}{M_1M}{}_2$ .

Par ailleurs, pour

M_1 M_2

constant :

\overset{⟶}{M_1 M}{}_2⋅d\overset{⟶}{M_1 M}{}_2=0

; or

\overset{→}{F}_{1→2}∥\overset{⟶}{M_1 M}{}_2

donc

δW_1+δW_2=0

; on obtient alors :

dE_c=∑_{\text{ext}} δW_i

.

◊ remarque : le travail des forces intérieures est donc indépendant du référentiel, puisque tout changement ne fait qu'ajouter une translation et une rotation d'ensemble sans déformation supplémentaire, d'où une contribution nulle.

◊ remarque : dans un référentiel non galiléen, il faut tenir compte des travaux des forces d’inertie d’entraînement ; par contre, les forces d’inertie complémentaires

\overset{→}{f}_{ci}=-2 \,m_i \; \overset{→}{ω} × \overset{→}{v}{}'_i

ne travaillent pas.

📖 exercices n° III, IV, V et VI.

Référentiel barycentrique

• On appelle “référentiel barycentrique” (noté ici

ℛ^*

) le référentiel d’origine

G

, en translation (quelconque) par rapport à un référentiel galiléen.

L’intérêt du référentiel barycentrique, généralement non galiléen, est de séparer l’étude du mouvement d’un système en une translation d’ensemble et une rotation-déformation par rapport à

G

.

• Dans le référentiel barycentrique, la propriété

\overset{→}{p}{}^{*}=\overset{→}{0}

impose que le moment cinétique

\overset{→}{L}{}^*

y est indépendant du point de référence (donc non précisé) ; d'un autre point de vue, cela impose que le travail des forces intérieures y est nul.

Une autre particularité utile est la propriété :

\overset{→}{L}{}^{*}=\overset{→}{L}_G

(dans

ℛ

galiléen) ; on en déduit :

{\displaystyle \frac{d\overset{→}{L}{}^*}{dt}}=∑_{\text{ext}} \overset{→}{ℳ}_{iG} =\overset{→}{ℳ}_G

sans forces d’inertie, même si le référentiel barycentrique n’est pas galiléen (ceci revient à dire que la somme des moments des forces d’inertie est toujours nulle).

Solide en rotation autour d'un axe fixe

• Pour un point

M

en rotation autour d’un point

O

(à distance

OM=r

constante), on obtient :

\overset{→}{L}_O=\overset{⟶}{OM} × m \;\overset{→}{v}=m \:r^2 \; \overset{→}{ω}

; on peut alors définir un “moment d’inertie”

J=m \:r^2

et écrire :

$\overset{→}{L}_O=J \;\overset{→}{ω}$ ; $\overset{→}{ℳ}_O=J \, {\displaystyle \frac{d\overset{→}{ω}}{dt}}$ ; $\widebar{L}_Δ=J \:ω$ ; $\widebar{ℳ}_Δ=J \,{\displaystyle \frac{dω}{dt}}$ .

Pour l'ensemble des points constituant un solide en rotation autour d'un axe fixe, avec des coordonnées cylindriques selon cet axe :

\overset{→}{L}_{Oi}=m \:r_i^{\:2} \; \overset{→}{ω}

(la vitesse angulaire est commune). On peut alors généraliser les lois précédentes en définissant un moment d’inertie total

J=∑ (m_i \: r_i^{\:2} \,)

.

• En pratique, il faut toutefois généralement calculer la somme par intégration ; ainsi pour un cylindre homogène, de rayon

R

et de longueur

𝓁

, tournant selon son axe :

J=∭μ \:r^2 \: dτ=μ .∫_0^R \,r^3 \: dr.∫_0^{2π} \,dθ.∫_0^𝓁 \,dz=μ \frac{1}{4} R^4 \: 2π \:𝓁

.

Ceci peut s'écrire en fonction de la masse du cylindre :

m=μ \frac{1}{2} R^2 \: 2π \:𝓁

; on obtient ainsi (dans ce cas particulier) :

J=\frac{1}{2} m \:R^2

.

• On peut aussi raisonner sur l'énergie cinétique :

$\overset{→}{v}_i=\overset{→}{ω} × \overset{⟶}{OM}_i=r_i \: ω \;\overset{→}{u}_{θi}$ ; $E_{ci}=\frac{1}{2} m_i \: r_i^{\:2} \: ω^2$ ;
$E_c=\frac{1}{2} \left( ∑ (m_i \: r_i^{\:2} \,) \right) \: ω^2=\frac{1}{2} J\: ω^2$ .

• D'un autre point de vue, lorsqu'on utilise des pièces mécaniques rotatives, on diminue l'usure et on améliore l'efficacité en “équilibrant” le dispositif :

centre d'inertie et axe de symétrie selon l'axe de rotation (les roues des voitures ont ainsi des masselottes placées sur le pourtour de la jante pour mieux équilibrer) ;

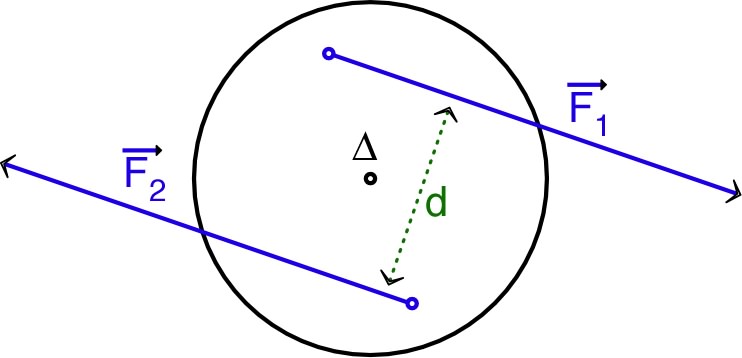
interactions par des “couples de forces” symétriques dont la somme est nulle ; sur le schéma ci-contre :

$\overset{→}{F}_1+\overset{→}{F}=\overset{→}{0}$ ;
$F_1=F_2$ (noté $F$ ) ;
$\widebar{ℳ}_Δ=-F\:d$ (noté $Γ$ ) .

📖 exercice n° VII.

Théorème du viriel

• On considère un système de

N

points matériels en interaction gravitationnelle (pouvant décrire une galaxie, un amas de galaxies...), supposé en équilibre statistique. Ce système est supposé rester borné ; il est étudié par rapport à son référentiel barycentrique, présumé quasi galiléen.

On note

\overset{→}{r}_i=\overset{⟶}{GM}_i

; le moment d'inertie

J=∑ (m_i \: r_i^{\:2} \,) =∑ (m_i \: \overset{→}{r}_i{}^2 \,)

est tel que :

{\displaystyle \frac{1}{2} \frac{d^2 J}{{dt}^2}} =∑ (m_i \; \overset{→}{r}_i⋅\ddot{\overset{→}{r}}_i \,) +∑ (m_i \: \dot{\overset{→}{r}}_i{}^2 \,)

.

Or, pour un système borné en équilibre statistique, on obtient en moyenne dans le temps :

\displaystyle \left\langle \,\frac{d^2 J}{{dt}^2}\, \right\rangle=\underset{t\text{’}→∞}{\lim}\: \left[ \frac{1}{t\text{’}} ∫_0^{t\text{’}} \frac{d^2 J}{{dt}^2} (t) \; dt \right]=0

.

• On peut de plus considérer :

\left〈 ∑ (m_i \:\overset{→}{r}_i⋅\ddot{\overset{→}{r}}_i \,) \right〉=\left\langle \,∑ \left( \,\overset{→}{F}_i⋅ \overset{→}{r}_i \,\right)\, \right\rangle

où les forces peuvent s'écrire :

\displaystyle \overset{→}{F}_i=-∑_{j\text{≠}i}\;\left(𝒢 \:m_i \: m_j \, \frac{\overset{→}{r}_i-\overset{→}{r}_j}{\left\|\,\overset{→}{r}_i-\overset{→}{r}_j \right\|^3} \right)

.

Ainsi, en combinant les indices :

$\displaystyle ∑_i \left( \,\overset{→}{F}_i⋅ \overset{→}{r}_i \right) =-∑_{i,j\text{≠}i} \left(𝒢 \:m_i \: m_j \frac{\overset{→}{r}_i⋅\left(\,\overset{→}{r}_i-\overset{→}{r}_j \right)}{\left\|\, \overset{→}{r}_i-\overset{→}{r}_j \right\|^3} \right) =-∑_{j,i\text{≠}j} \left(𝒢 \:m_j \: m_i \frac{\overset{→}{r}_j⋅\left(\,\overset{→}{r}_j-\overset{→}{r}_i \right)}{\left\|\, \overset{→}{r}_j-\overset{→}{r}_i \right\|^3} \right)$ ;

$\displaystyle =-\frac{1}{2} \,∑_{i,j\text{≠}i} \left(𝒢 \:m_i \: m_j \:\left[ \frac{\overset{→}{r}_i⋅\left(\,\overset{→}{r}_i-\overset{→}{r}_j \right)}{\left\|\,\overset{→}{r}_i-\overset{→}{r}_j \right\|^3} +\frac{\overset{→}{r}_j⋅\left(\,\overset{→}{r}_j-\overset{→}{r}_i \right)}{\left\|\,\overset{→}{r}_j-\overset{→}{r}_i \right\|^3} \right]\right)$ ;
$\displaystyle =-\frac{1}{2} \,∑_{i,j\text{≠}i} \left(𝒢 \:m_i \: m_j \,\frac{\left(\overset{→}{r}_i-\overset{→}{r}_j \right)^2}{\left\|\,\overset{→}{r}_i-\overset{→}{r}_j \right\|^3} \right) =-\frac{1}{2} \,∑_{i,j\text{≠}i} \left(\frac{𝒢 \:m_i \: m_j}{\left\|\,\overset{→}{r}_i-\overset{→}{r}_j \right\|} \right) ={\textstyle \frac{1}{2} \,∑_i (m_i \: 𝒱_i )}$ .

Compte tenu du fait qu'en faisant la somme des énergies potentielles d'interaction des masses

m_i

dans un potentiel

𝒱_i=𝒱(M_i )

on compte deux fois les interactions des paires

(ij)

, on obtient finalement :

∑_i \left( \,\overset{→}{F}_i⋅ \overset{→}{r}_i \right) =E_p

.

• Par ailleurs :

∑ (m_i \: \dot{\overset{→}{r}}{}_i^{\:2}\, ) =2 \,E_c

; donc au total :

0=〈 E_p 〉+2 〈 E_c 〉

.

Ceci généralise une propriété déjà remarquée pour un satellite en orbite circulaire :

E_p=-2 \,E_c

(où ces énergies sont dans ce cas constantes).