DYNAMIQUE - SYSTÈMES DE POINTS - corrigé des exercices

A. EXERCICES DE BASE

Poussah

• Par symétrie, les centres d’inertie respectifs

G_1

G_2

du cylindre et de la demi-sphère sont sur l’axe et

\displaystyle OG_1=\frac{h}{2}

dynSystemes_cor_Im/dynSystemes_cor_Im3.jpg

dynSystemes_cor_Im/dynSystemes_cor_Im4.jpg

• Le calcul de la position de

G_2

(non demandé par l'énoncé) est plus compliqué car il correspond à une somme intégrale sur la répartition de masse dans la demi-sphère :

m_2 \; \overset{⟶}{OG}_2=∭ \:\overset{→}{r} \: dm

où

\overset{→}{r}=\overset{⟶}{OM}

avec

M

point quelconque de la demi-sphère. Par symétrie :

m_2 \:OG_2=∭ z \:dm=∭ r \;\cos(θ) \: dm

.
• Pour un élément de volume en coordonnées sphériques :

dm=ρ_2 \: dr \;r \:dθ \;r \; \sin(θ) \: dϕ

;

$m_2 \: OG_2=ρ_2 \: ∭ r^3 \; \cos(θ) \: \sin(θ) \: dr \:dθ \:dϕ=2π \:ρ_2 \: ∬ r^3 \; \cos(θ) \: \sin(θ) \: dr \:dθ=π \:ρ_2 \: ∫ r^3 \: dr$ ;
$\displaystyle m_2 \:OG_2=π \:ρ_2 \frac{R^4}{4}$ .

dynSystemes_cor_Im/dynSystemes_cor_Im5.jpg

• Compte tenu de

m_2=ρ_2 \: V=\frac{2}{3} π \:ρ_2 \: R^3

ceci correspond à

OG_2=\frac{3}{8} R

.
• La condition pour que

G

soit en

O

correspond par suite à :

m_1 \:OG_1=m_2 \:OG_2

d’où on déduit (avec

m_1=ρ_1 \: π \:R^2 \: h

) :

\displaystyle h=R\sqrt{\frac{ρ_2}{2 \,ρ_1}}

• On obtient numériquement :

h=2\text{,}65 \:\mathrm{cm}

• Si

G

est confondu avec

O

, sa hauteur au dessus de la surface sur laquelle est posé l’ensemble est indépendante de l’inclinaison du système ; donc l’énergie potentielle de pesanteur de ce dernier ne dépend pas de l’inclinaison et il est donc en équilibre indifférent.

Équilibre

• On repère les blocs de sucre par l’abscisse de leur côté gauche par rapport au côté gauche du premier (celui du dessus) ; ainsi

x_1=0

. Pour que le bloc n° 1 soit en équilibre sur le bloc n° 2, il faut :

\displaystyle x_2≤x_{G_1}=\frac{𝓁}{2}

(en notant

𝓁

la longueur d'un bloc).
• De même, pour que l’ensemble

\{1+2\}

soit en équilibre sur le bloc n° 3, il faut :

x_3≤x_{G_2}

(où

G_2

représente le centre de gravité de l’ensemble des deux) ; mais :

\displaystyle x_{G_2}=\frac{1}{2} \left[x_{G_1}+\left(x_2+\frac{𝓁}{2}\right)\right]≤\frac{3 \,𝓁}{4}

donc il faut

\displaystyle x_3≤\frac{3 \,𝓁}{4}

.
• En raisonnant de même et en considérant qu’on prend toujours le cas limite (pour simplifier l’écriture des inégalités) :

\displaystyle x_{n+1}=x_{G_n}=\frac{1}{n} \left[(n-1) \:x_{G_{(n-1)}}+\left(x_n+\frac{𝓁}{2}\right)\right]=x_n+\frac{𝓁}{2 \,n}=x_1+\frac{𝓁}{2} \, {\textstyle ∑_1^n \left(\frac{1}{k}\right)}

.
• Compte tenu de

x_1=0

, la condition :

x_{n+1}≥𝓁

correspond à :

∑_1^n \left( \frac{1}{k}\right) ≥2

. Il n’y a pas de méthode algébrique évidente pour résoudre cette équation, mais la méthode numérique montre rapidement que

x_5≥𝓁

et qu'il faudrait donc au minimum cinq blocs :

$∑_1^1 \left(\frac{1}{k}\right) =1$ ; $∑_1^2 \left(\frac{1}{k}\right) =\frac{3}{2}$ ; $∑_1^3 \left(\frac{1}{k}\right) =\frac{11}{6}$ ; $∑_1^4 \left(\frac{1}{k}\right) =\frac{25}{12}>2$ .

• En pratique toutefois, le placement des blocs en équilibre nécessite une marge de sécurité d'au moins

5 \,%

; on obtient ainsi :

$\displaystyle x_2≤x_{G_1}-\frac{𝓁}{20}=\frac{𝓁}{2}-\frac{𝓁}{20}=\frac{9\,𝓁}{20}$ ; $\displaystyle x_3≤x_{G_2}-\frac{𝓁}{20}≤\frac{1}{2} \left[x_{G_1}+\left(x_2+\frac{𝓁}{2}\right)\right] -\frac{𝓁}{20}≤\frac{3}{2}\,\frac{9\,𝓁}{20}$ ;
$\displaystyle x_{n+1}=x_{G_n}-\frac{𝓁}{20}=\frac{1}{n} \left[(n-1)\:x_{G_{(n-1)}}+\left(x_n+\frac{𝓁}{2}\right)\right] -\frac{𝓁}{20}=x_n+\frac{1}{n}\,\frac{9\,𝓁}{20}=x_1+ \frac{9\,𝓁}{20} \, {\textstyle ∑_1^n \left(\frac{1}{k}\right)}$ .

• Il faut alors un sixième bloc pour obtenir :

∑_1^5 \left(\frac{1}{k}\right)=\frac{137}{60}>\frac{20}{9}

Centre d’inertie

• Puisque les points

A

B

G

sont alignés, on peut considérer simplement le centre d’inertie

I

de l’ensemble :

m \;\overset{⟶}{IG}+m_A \;\overset{⟶}{IA}+m_B \;\overset{⟶}{IB}=\overset{→}{0}

.
• Il en est de même après le déplacement, compte tenu du fait que le centre d’inertie de l’ensemble est immobile pour un système pseudo-isolé (le poids est compensé par la poussée d’Archimède et les frottements sont négligeables) :

m \;\overset{⟶}{IG}{}'+m_A \;\overset{⟶}{IA}{}'+m_B \;\overset{⟶}{IB}{}'=\overset{→}{0}

.
• On en déduit par différence :

m \;\overset{⟶}{GG}{}'+m_A \;\overset{⟶}{AA}{}'+m_B \;\overset{⟶}{BB}{}'=\overset{→}{0}

.
• Mais les déplacements de

A

B

sont la somme d’un déplacement d’entraînement de la barque et d’un déplacement relatif dans la barque :

\overset{⟶}{AA}{}'=\overset{⟶}{GG}{}'+\overset{⟶}{AB}=\overset{→}{𝒹}+\overset{→}{𝓁}

\overset{⟶}{BB}{}'=\overset{⟶}{GG}{}'+\overset{⟶}{BA}=\overset{→}{𝒹}-\overset{→}{𝓁}

; par suite :

(m+m_A+m_B) \;\overset{→}{𝒹}=(m_A-m_B) \;\overset{→}{𝓁}

et finalement :

\displaystyle 𝒹=𝓁 \:\frac{|m_A-m_B |}{m+m_A+m_B}

Quantité de mouvement totale

• Par conservation de la quantité de mouvement totale (résultante cinétique) du système pseudo-isolé (le poids est compensé par la réaction du coussin d’air et on suppose les frottements négligeables) :

$m_1 \; \overset{→}{v}_1+m_2 \; \overset{→}{v}_2=(m_1+m_2 ) \; \overset{→}{v}{}'$ et donc : $\displaystyle \overset{→}{v}{}'=\frac{m_1 \; \overset{→}{v}_1+m_2 \; \overset{→}{v}_2}{m_1+m_2}$ .

Énergie mécanique

1.	• En supposant que le ressort ne fléchit pas, son allongement est : $𝓁-𝓁_0=x_2-x_1-𝓁_0$ ; la relation fondamentale de la dynamique appliquée aux deux mobiles (algébriquement le long de l’axe) donne alors : $m_1 \: \ddot{x}_1=k .(x_2-x_1-𝓁_0)$ et $m_2 \: \ddot{x}_2=-k .(x_2-x_1-𝓁_0)$ .

2.	• La somme de ces deux équations est : $(m_1+m_2) \:\ddot{x}_G=0$ ; on retrouve donc que le centre d’inertie du système pseudo-isolé a un mouvement rectiligne uniforme.

• La combinaison linéaire indiquée donne :

m_1 \:\dot{x}_1 \: \ddot{x}_1+m_2 \: \dot{x}_2 \: \ddot{x}_2= -k .(x_2-x_1-𝓁_0) \,(\dot{x}_2-\dot{x}_1)

.
• Ceci peut s’écrire :

2 \,\dot{E}_c=-2 \,\dot{E}_p

avec :

E_c=\frac{1}{2} \left(m_1 \: \dot{x}_1^{\:2}+m_2 \: \dot{x}_2^{\:2} \right)

E_p=\frac{1}{2} k .(x_2-x_1-𝓁_0)^2

. On aboutit donc à la conservation de l’énergie mécanique :

\dot{E}_m=0

avec

E_m=E_c+E_p

• Les oscillations correspondent au mouvement relatif et leur étude suppose qu’on mette en évidence la quantité

x_2-x_1

; en multipliant la première équation du mouvement par

m_2

et la seconde par

m_1

, puis en calculant la différence :

m_1 \: m_2 \: (\ddot{x}_2-\ddot{x}_1 )=-(m_1+m_2) \:k .(x_2-x_1-𝓁_0)

.
• En posant :

ξ=x_2-x_1-𝓁_0

\displaystyle μ=\frac{m_1 \: m_2}{m_1+m_2}

(nommée “masse réduite”) l’équation peut s’écrire :

\displaystyle \ddot{ξ}+\frac{k}{μ} \, ξ=0

, correspondant à des oscillations de pulsation

\displaystyle ω=\sqrt{\frac{k}{μ}}

et de période

\displaystyle T=\frac{2π}{ω}=2π \,\sqrt{\frac{μ}{k}}

Travail des forces intérieures et changement de référentiel

• Lors du changement de référentiel, on peut considérer

\overset{→}{v}{}'_i=\overset{→}{v}_i+\overset{→}{v}_e

avec une vitesse d'entraînement (dépendant du point) :

\overset{→}{v}_e=\overset{→}{v}_O+\overset{→}{ω}× \overset{⟶}{OM}_i

.
• En raisonnant sur la somme de deux actions réciproques :

$𝒫'=\overset{→}{F}_{2→1}⋅\overset{→}{v}{}'_1+\overset{→}{F}_{1→2}⋅\overset{→}{v}{}'_2= 𝒫+\overset{→}{F}_{2→1}⋅\left(\overset{→}{v}_O+\overset{→}{ω}× \overset{⟶}{OM}_1\right)+\overset{→}{F}_{1→2}⋅\left(\overset{→}{v}_O+\overset{→}{ω} × \overset{⟶}{OM}_2\right)$ ;
$𝒫'=𝒫+\overset{→}{F}_{1→2}⋅\left(\overset{→}{ω}×\overset{⟶}{M_1 M}_2 \right)=𝒫$ puisque $\overset{→}{F}_{1→2}∥ \overset{⟶}{M_1 M}_2$ .

• Il en est par suite de même pour

δW=𝒫 \:dt

Machine d'Atwood

• Pour étudier le dispositif complexe par la méthode demandée il est préférable d'étudier séparément les différentes parties.
• Pour le point matériel

M

, le principe fondamental peut s'écrire :

m\; \overset{→}{a}=\overset{→}{P}+\overset{→}{T}

; en projection sur un axe vertical, ceci donne :

m \:\ddot{z}=-m \:g+T

.
◊ remarque : on peut aussi obtenir ce résultat d'après le théorème du moment cinétique par rapport à

O

, en notant

\overset{→}{u}_Δ

le vecteur unitaire de l'axe de rotation, orienté vers l'arrière du schéma ;

∑ \overset{→}{ℳ}_O =\overset{⟶}{OM} × \left(\overset{→}{P}+\overset{→}{T}\, \right)=\dot{\overset{→}{L}}_O=\overset{⟶}{OM} × m \:\overset{→}{a}

; donc algébriquement :

∑ \widebar{ℳ}_∆ =R .(-m \:g+T\,)=\dot{\widebar{L}}_∆=R \:m \:\ddot{z}

(mais c'est moins simple).
• Par analogie pour le point matériel

M'

m' \:\ddot{z}{}'=-m' \:g+T'

.
• Le fil étant inextensible,

z'

augmente d'autant que

z

diminue, donc

z+z'

est constant ; ceci implique la relation :

\ddot{z}+\ddot{z}{}'=0

dynSystemes_cor_Im/dynSystemes_cor_Im1.jpg

• Pour ce qui concerne la poulie, la masse négligeable du fil fait qu'il transmet la tension (ici vers le bas). Par ailleurs, le poids et la réaction du support ont un moment nul par rapport à l'axe. Le théorème du moment cinétique peut s'écrire algébriquement :

∑ \widebar{ℳ}_∆ =R .(T'-T\,)=\dot{\widebar{L}}_∆=J \:\dot{ω}=J \:\ddot{θ}

.
• Si le fil est idéal, il se déplace d'autant que la rotation de la poulie (sans glisser) :

dz=R \:dθ

; ceci implique la relation :

\ddot{z}=R \:\ddot{θ}

dynSystemes_cor_Im/dynSystemes_cor_Im2.jpg

• Il suffit alors de combiner les relations pour étudier en fonction de la variable choisie, par exemple

z

$R^2 .(T'-T\,)=J \:R \:\ddot{θ}=J \:\ddot{z}$ ;
$T'-T=m' .(\ddot{z}{}'+g)-m .(\ddot{z}+g)=-(m+m') \: \ddot{z}+(m'-m) \: g$ ;
$\displaystyle \left(m+m'+\frac{J}{R^2} \right) \: \ddot{z}=(m'-m) \: g$ .

◊ remarque : les effets des masses pesantes de part et d'autre tendent à se compenser, mais les effets d'inertie s'ajoutent.

• L'énergie cinétique peut s'écrire :

E_c=\frac{1}{2} m \:\dot{z}^2+\frac{1}{2} \,(2 \,m') \: {\dot{z}{}'}^2+\frac{1}{2} J \:ω^2

.
• Pour un fil idéal :

\dot{z}=R \:ω=R \:\dot{θ}=-2 \,\dot{z}{}'

(pour un même angle, la longeur d'enroulement varie deux fois moins à droite) ;

\displaystyle E_c=\frac{1}{2} \left(m+\frac{m'}{2}+\frac{J}{R^2} \right) \; \dot{z}{}^2

.
• L'énergie potentielle peut s'écrire :

E_p=m \:g \:z+(2 \,m') \: g \:z'+Cste

(la poulie tourne sur place et peut être omise). Mais

z+2 \,z'=Cste

;

E_p=(m-m') \: g \:z+Cste

.
• Ceci donne l'énergie mécanique :

\displaystyle E_m=E_c+E_p=\frac{1}{2} \left(m+\frac{m'}{2}+\frac{J}{R^2} \right) \; \dot{z}^2+(m-m') \: g \:z+Cste

.
• On obtient en dérivant :

\displaystyle \dot{E}_m=0=\left[\left(m+\frac{m'}{2}+\frac{J}{R^2} \right) \; \ddot{z}+(m-m') \: g\right] \; \dot{z}

; l'équation du mouvement correspond à

\dot{z}≠0

et donc :

\displaystyle \left(m+\frac{m'}{2}+\frac{J}{R^2} \right) \; \ddot{z}=(m'-m) \: g

.
◊ remarque : les effets des masses pesantes de part et d'autre tendent à se compenser (le doublement de

m'

compensant le rayon divisé par deux) ; les effets d'inertie s'ajoutent mais

m'

“seulement” doublée y contribue moins car son déplacement moindre intervient au carré.

B. EXERCICES D'APPROFONDISSEMENT

Travail des forces d'inertie et référentiel barycentrique

• Le travail des forces d'inertie de Coriolis est toujours nul puisque ces forces sont perpendiculaires au mouvement relatif.
• Si

ℛ^*

n'est pas galiléen (s'il est en translation accélérée), la puissance des forces d'inertie d'entraînement aussi y est nulle :

𝒫_e^* =∑ \left(-m_i \; \overset{→}{a}_G⋅\overset{→}{v}{}_i^* \right) =-\overset{→}{a}_G⋅\overset{→}{p}{}^* =0

; donc de même pour

δW_e^* =𝒫_e^* \: dt

Centre d’inertie

• Par symétrie, le centre d’inertie

G

du demi-cercle est sur l’axe.
• Sa position se déduit du calcul d’une intégrale sur la répartition de masse dans le demi-cercle ; en notant

\overset{→}{r}=\overset{⟶}{OM}

avec

M

point quelconque du demi-cercle :

m \;\overset{⟶}{OG}=∫ \,\overset{→}{r} \: dm

.
• Par symétrie :

m \:OG=∫ \,z \:dm=∫ \,R \:\cos(θ)\:dm

dynSystemes_cor_Im/dynSystemes_cor_Im6.jpg

• Par ailleurs, pour un élément de longueur infinitésimal en coordonnées polaires :

dm=λ \:R \:dθ

(où

λ

est la masse linéique). Par suite :

m \:OG=λ \:R^2 \:∫ \,\cos(θ)\:dθ=2 \,λ \:R^2

et compte tenu de

m=π \:R \:λ

ceci correspond à

\displaystyle OG=\frac{2 \,R}{π}

.
◊ remarque : on considère une répartition linéique car l’énoncé indique que la tige est mince.

• Par symétrie, le centre d’inertie

G

du demi-cylindre est sur l’axe.
• Sa position se déduit du calcul d’une intégrale sur la répartition de masse dans le demi-cylindre ; on obtient de façon analogue :

m \;\overset{⟶}{OG}=∭ \,\overset{→}{r} \: dm

.
• Par symétrie :

m \:OG=∭ \,z \:dm=∭ \,R \:\cos(θ)\:dm

.
• Par ailleurs, en coordonnées cylindriques (avec

ρ

masse volumique) :

dm=ρ \:dr \:r \,dθ \:dz

dynSystemes_cor_Im/dynSystemes_cor_Im7.jpg

• Par conséquent :

$m \:OG=ρ \:∭\,r^2 \; \cos(θ)\:dr \:dθ \:dz=ρ \:h \:∬\,r^2 \; \cos(θ)\:dr \:dθ=2 \,ρ \:h \:∫\,r^2 \: dr=\frac{2}{3} ρ \:h \:R^3$ .

• Compte tenu de

m=∭ dm=ρ \, \frac{π}{2} h \:R^2

ceci correspond à

\displaystyle OG=\frac{4 \,R}{3π}

Théorèmes de Kœnig

1.a.	• Dans $ℛ$ galiléen, le changement de centre de référence correspond à : $\overset{→}{L}_O=∑ \left(\overset{⟶}{OM}_i × \overset{→}{p}_i \right) =\overset{⟶}{OG} × ∑ \,\overset{→}{p}_i +∑ \left(\overset{⟶}{GM}_i × \overset{→}{p}_i \right) =\overset{⟶}{OG} × \overset{→}{p}+\overset{→}{L}_G$ .

1.b.	• On obtient par ailleurs : $\overset{→}{L}_G=∑ \left(\overset{⟶}{GM}_i × m_i \; \overset{→}{v}_G \right) +∑ \left(\overset{⟶}{GM}_i × m_i \; \overset{→}{v}{}_i^* \right) =∑ \left(m_i \; \overset{⟶}{GM}_i \right) × \overset{→}{v}_G+\overset{→}{L}{}_G^* =\overset{→}{L}{}_G^$ et finalement : $\overset{→}{L}_O=\overset{⟶}{OG} × \overset{→}{p}+\overset{→}{L}{}_G^$ .

• D’une façon analogue pour l’énergie cinétique :

$E_c=∑ E_{ci} =∑ \left(\frac{1}{2} m_i \: v_i^{\:2} \right) =∑ \left(\frac{1}{2} m_i \: v_G^{\:2} \right) +∑ \left(\frac{1}{2} m_i \:v_i^{*2} \right) +∑ \left(m_i \; \overset{→}{v}_G⋅\overset{→}{v}{}_i^* \right)$ ;
$E_c=\frac{1}{2} (∑ m_i ) \: v_G^{\:2}+E_c^*+\overset{→}{v}_G⋅∑ \,\overset{→}{p}{}_i^* =\frac{1}{2} (∑ m_i ) \: v_G^{\:2}+E_c^*$ .

Énergie cinétique et moment cinétique

• D’après le théorème de Kœnig :

E_c=\frac{1}{2} (m_1+m_2 ) \: V^2+E_c^*

où

V=A \:Ω

est la vitesse du mouvement de

G

autour du Soleil et où

E_c^*

est l’énergie cinétique “relative” dans le référentiel barycentrique.
• En utilisant :

E_c^* =\frac{1}{2} m_1 \: v_1^{\:2}+\frac{1}{2} m_2 \: v_2^{\:2}

avec

v_1=r_1\: ω

v_2=r_2 \: ω

, il suffit d’utiliser les propriétés du barycentre pour calculer

r_1

r_2

. On obtient ainsi :

\displaystyle r_1=𝓁 \: \frac{m_2}{m_1+m_2}

\displaystyle r_2=𝓁 \: \frac{m_1}{m_1+m_2}

; par suite :

\displaystyle E_c^* =\frac{1}{2} \frac{m_1 \: m_2}{m_1+m_2} \: 𝓁^2 \: ω^2

.
• Finalement :

E_c=\frac{1}{2} M \:A^2 \: Ω^2+\frac{1}{2} μ \:𝓁^2 \: ω^2

avec

M=m_1+m_2

(masse totale) et

\displaystyle μ=\frac{m_1 \: m_2}{m_1+m_2}

(nommée masse réduite).

• D’après le théorème de Kœnig :

\overset{→}{L}_O=\overset{⟶}{OG} × (m_1+m_2 ) \; \overset{→}{V}+\overset{→}{L}{}_G^*

où

\overset{→}{V}

est la vitesse du mouvement de

G

autour du Soleil et où

\overset{→}{L}{}_G^*

est le moment cinétique “relatif” dans le référentiel barycentrique.
• En utilisant :

\overset{→}{L}{}_G^* =m_1 \: r_1 \: v_1 \: \overset{→}{u}_z+m_2 \: r_2 \: v_2 \: \overset{→}{u}_z

avec

v_1=r_1 \: ω

v_2=r_2 \: ω

\overset{→}{u}_z

vecteur unitaire orienté selon

\overset{→}{ω}

\overset{→}{Ω}

, on obtient :

\overset{→}{L}{}_G^* =μ \:𝓁^2 \: ω \;\overset{→}{u}_z

.
• Finalement :

\overset{⟶}{OG} × \overset{→}{V}=A^2 \: Ω \;\overset{→}{u}_z

donc

\overset{→}{L}_O=M \:A^2 \: Ω \;\overset{→}{u}_z+μ \:𝓁^2 \: ω \;\overset{→}{u}_z

Tourniquet de Mach-Feynman

1.a.

• Les deux sorties

S_1

S_2

ayant des effets symétriques sur le moment cinétique, on peut simplifier l'écriture en doublant l'effet d'une sortie notée

S

. L'effet de

E

, sur l'axe, est nul.
• Le dispositif étant ouvert, on raisonne sur la variation du contenu entre deux instants séparés par une durée infinitésimale

dt

, pendant laquelle circule une masse

dm = ρ \:D \:dt

. Le système fermé étudié correspond au contenu “initial”, dont une quantité d'eau est ensuite sortie.
• La pesanteur, verticale, n'a pas d'effet sur la rotation. En négligeant les frottements, le théorème du moment cinétique peut s'écrire :

\left[\overset{→}{L}_O (t+dt)+2 \,dm \:\overset{⟶}{OS} × \overset{→}{V} \,\right]-\left[\overset{→}{L}_O (t)\right]=\overset{→}{0}

.
• La vitesse de l'eau éjectée est

\overset{→}{V}=𝓁 \:\dot{θ} \; \overset{→}{u}_θ+\overset{→}{v}

où

\overset{→}{v}

est la vitesse relative par rapport au tourniquet (on néglige le diamètre du tube en comparaison de sa longueur). Ainsi :

$dL_z+2 \,ρ \:D \:dt \:𝓁 .[𝓁 \:\dot{θ}-v \;\cos(α) ]=0$ avec $D=s \:v$ .

dynSystemes_cor_Im/dynSystemes_cor_Im8.jpg

• Puisque la quantité d'eau contenue dans le tourniquet est constante (même si ce n'est pas toujours la même eau), on peut supposer que le moment cinétique peut être décrit à l'aide d'un moment d'inertie :

L_z=J \:\dot{θ}

. Ceci donne :

J \:\ddot{θ}+2 \,ρ \:D \:𝓁 .[𝓁 \:\dot{θ}-v \;\cos(α) ]=0

1.b.

• On note

R

le rayon du début du coude et on suppose pour simplifier que l'angle du tube avec

\overset{→}{u}_θ

est constant entre

R

𝓁

(ceci suppose que le coude correspond à une spirale exponentielle

r∝e^{λθ}

).
• En notant

L_{z0}

le moment cinétique du tube, on peut considérer la vitesse de l'eau à l'intérieur :

$\overset{→}{V}=v \;\overset{→}{u}_r+r \:\dot{θ} \; \overset{→}{u}_θ$ puis $\overset{→}{V}=v \; \sin(α) \; \overset{→}{u}_r+[r \:\dot{θ}-v \;\cos(α) ] \; \overset{→}{u}_θ$ ;
$L_z=L_{z0}+∫_0^R \,r^2 \: \dot{θ} \: ρ \:s \:dr+{\displaystyle ∫_R^𝓁 r .[r \:\dot{θ}-v \;\cos(α) ] \: \frac{ρ \:s}{sin⁡(α)} \: dr}$ ;
$L_z=(J_0+J_e ) \: \dot{θ}+ς_v$ avec :

$J_0$ pour le tube ; $\displaystyle J_e=ρ \:s .\left[\frac{R^3}{3}+\frac{𝓁^3-R^3}{3 \:\sin(α)}\right]$ pour la rotation sans écoulement de l'eau ;
$\displaystyle ς_v=-ρ \:s \; \cotan(α) \: v \: \frac{𝓁^2-R^2}{2}$ pour l'écoulement de l'eau.

• On obtient effectivement

\dot{L}_z=(J_0+J_e ) \: \ddot{θ}

sans influence de l'écoulement de l'eau, mais ce n'est pas aussi évident qu'on aurait pu le penser a priori.

1.c.

• En notant

ω=\dot{θ}

\displaystyle Ω=\frac{v}{𝓁} \: \cos(θ)

\displaystyle \frac{1}{τ}=\frac{2 \,ρ \:D \:𝓁^2}{J}

, l'équation peut s'écrire :

\dot{ω}+\frac{1}{τ} \, (ω-Ω)=0

.
• Pour une vitesse initiale nulle, on obtient la solution :

ω=Ω .\left(1-\mathrm{e}^{-t/τ} \right)

.
• La vitesse limite

Ω

correspond au cas où la vitesse d'éjection est radiale :

ℓ \:\dot{θ} - v \;\cos(α) = 0

1.d.

• Si on suppose le tube initialement vide (rempli d'air), la rotation du tourniquet commence dès que du liquide passe le coude : si l'interaction avec le tube dévie l'eau dans le sens horaire, alors l'action réciproque met le tube en mouvement dans le sens contraire. L'éjection en sortie est sans effet si on peut négliger l'interaction avec l'air extérieur.

dynSystemes_cor_Im/dynSystemes_cor_Im9.jpg

• La mécanique des fluides permet de préciser. Pour un fluide “parfait” incompressible, en régime stationnaire, la conservation de l'énergie peut s'exprimer par la relation de Bernoulli le long d'une ligne de courant :

\frac{1}{2} ρ \:v^2+ρ \:g \:z+p=Cste

(ici le terme avec

z≈Cste

peut être omis). Or l'incompressibilité fait que la vitesse diminue là où les lignes de courant s'écartent, donc la pression augmente (la différence de pression, donc de forces pressantes de part et d'autre, correspond au ralentissement).
• Le calcul des lignes de courant (hors sujet ici) montre que, du côté externe du virage, la pression intérieure est plus grande que la pression extérieure ; inversement la pression intérieure est plus petite que la pression extérieure pour le côté interne du virage. Ces deux effets (Venturi) sont la cause de l'interaction précédente (qui peut toutefois être comprise intuitivement sans mécanique des fluides) entraînant le tourniquet dans le sens anti-horaire.

2.a.

• Le transfert de rotation au fluide extérieur, à cause de l'éjection, tend à en faire tourner le voisinage dans le sens horaire, mais l'interaction (par frottements) avec le tube fait aussi un peu d'effet contraire. On suppose ici qu'on peut qualitativement négliger ceci et considérer le fluide extérieur immobile, mais son léger mouvement d'ensemble peut en réalité modifier un peu

Ω

τ

(le mouvement par rapport au référentiel diffère du mouvement par rapport au milieu).
• Il faut raisonnablement prendre en compte un frottement ; un effet visqueux est plausible.

• En plus de l'interaction au niveau du coude, il peut maintenant y avoir une interaction avec le fluide extérieur au moment de l'éjection. Sans utiliser la mécanique des fluides, on peut penser possible que seule une proportion

β

de l'impulsion éjectée soit transmise au milieu extérieur ; par exemple la répartition de la pression peut appliquer une partie de l'effet au récipient fixe, sans transmission au fluide. La prise en compte d'un tel effet revient à multiplier

ρ \:D

donc

\displaystyle \frac{1}{τ}

par

β<1

, donc l'approche de la vitesse limite

Ω

est ralentie.
◊ remarque : même sans connaître le mécanisme exact, cela implique que le fluide sortant soit ralenti, donc un peu “dispersé” de part et d'autre (selon les lignes de courant) puisqu'il est incompressible ; en outre, selon la déviation du courant, qui peut dépendre de

\dot{θ}

, cela pourrait aussi influencer

Ω

.

• La mécanique des fluides permet de préciser. Le fluide sortant arrive atteint l'extrémité du tube avec une vitesse trop grande pour que les lignes de courant puisse suivre le bord de la surface et il se produit un “décollement” : le liquide sort sous forme de jet dans le fluide extérieur.
◊ remarque : si la viscosité n'est pas négligeable, le fluide entourant le jet peut aussi être entraîné avec un effet de frottement, mais ce n'est pas ce qui est considéré ici.

dynSystemes_cor_Im/dynSystemes_cor_Im10.jpg

dynSystemes_cor_Im/dynSystemes_cor_Im11.jpg

• Or l'interaction avec le bord tend à causer un “évasement” du jet, donc un ralentissement du fluide, donc ceci revient à éjecter une quantité de mouvement plus faible. Mais réciproquement, cela correspond à une pression plus faible à l'intérieur du tube, ainsi le bilan des forces pressantes intérieures et extérieures au niveau du coude (non symétrique) donne une résultante tendant à entraîner le tube dans le sens horaire, donc à diminuer l'effet obtenu précédemment.

2.b.

• Avec un frottement fluide visqueux, l'équation devient :

J \:\ddot{θ}+2 \,ρ \:D \:𝓁 .[𝓁 \:\dot{θ}-v \;\cos(α) ]=-k \:\dot{θ}

.
• Ceci peut aussi s'écrire :

\displaystyle J \:\ddot{θ}+2 \,ρ \:D \:𝓁 .\left[\left(𝓁+\frac{k}{2 \,ρ \:D \:𝓁}\right) \; \dot{θ}-v \;\cos(α) \right]=0

.
• La vitesse limite est diminuée :

\displaystyle Ω'=\frac{v}{𝓁+\frac{k}{2 \,ρ \:D \:𝓁}} \: \cos(θ)

; la constante de temps est diminuée dans les mêmes proportions :

\displaystyle \frac{1}{τ'}=\frac{2 \,ρ \:D \:𝓁}{J} \: \left(𝓁+\frac{k}{2 \,ρ \:D \:𝓁}\right)

.
◊ remarque : la durée

τ

plus courte n'est pas contradictoire car elle l'est dans les mêmes proportions que

Ω

; en particulier l'accélération initiale

\displaystyle ≈\frac{Ω}{τ}

correspondant à un frottement nul est inchangée.

3.a.

• Si on considère simplement que le liquide entrant à l'extrémité du tube a une vitesse relative

\overset{→}{v}

de sens contraire, on obtient :

$\left[\overset{→}{L}_O (t+dt)\right]-\left[\overset{→}{L}_O (t)+2 \,dm \;\overset{⟶}{OS} × \overset{→}{V} \right]=\overset{→}{0}$ ;
$\overset{→}{V}=𝓁 \:\dot{θ}\; \overset{→}{u}_θ+\overset{→}{v}$ (où $\overset{→}{v}$ est de sens contraire) ;
$dL_z-2 \,ρ \:D \:dt \:𝓁 .[𝓁 \:\dot{θ}+v \;\cos(α) ]=0$ ;
$J \:\ddot{θ}-2 \,ρ \:D \:𝓁 .[𝓁 \:\dot{θ}+v \;\cos(α) ]=0$ .

• Avec les notations précédentes, l'équation peut s'écrire :

\displaystyle \dot{ω}-\frac{1}{τ} \, (ω+Ω)=0

.
• Pour une vitesse initiale nulle, on obtient la solution divergente :

ω=-Ω .\left(1-\mathrm{e}^{t/τ} \,\right)

.
◊ remarque : pour toute vitesse initiale

ω_0≠-Ω

(correspondant au cas

𝓁 \:\dot{θ}+v \;\cos(α)=0

où la vitesse d'admission est radiale), on obtient de même une solution divergente.
• Bien que le système soit déformable, donc qu'une augmentation de l'énergie cinétique puisse être causée par un travail des forces intérieures, le caractère divergent suggère un défaut de modélisation.
◊ remarque : contrairement à ce que le cas particulier

ω=-Ω

pourrait laisser penser, la divergence se fait vers les valeurs de

ω

positives.

3.b.

• Avec un frottement fluide visqueux, l'équation devient :

J \:\ddot{θ}-2 \,ρ \:D \:𝓁 .[𝓁 \:\dot{θ}+v \;\cos(α) ]=-k \:\dot{θ}

.
• Ceci peut aussi s'écrire :

J \:\ddot{θ}-2 \,ρ \:D \:𝓁 .\left[\left(𝓁-\frac{k}{2 \,ρ \:D \:𝓁}\right) \; \dot{θ}+v \;\cos(α) \right]=0

.
• La vitesse limite est augmentée (en valeur absolue) :

\displaystyle Ω'=\frac{v}{𝓁-\frac{k}{2 \,ρ \:D \:𝓁}} \: \cos(θ)

; la constante de temps est augmentée dans les mêmes proportions :

\displaystyle \frac{1}{τ'}=\frac{2 \,ρ \:D \:𝓁}{J} \: \left(𝓁-\frac{k}{2 \,ρ \:D \:𝓁}\right)

.
• Certes, ici encore

τ

Ω

augmentent dans les mêmes proportions, donc l'accélération initiale

\displaystyle ≈\frac{Ω}{τ}

correspondant à un frottement nul est inchangée. Certes, un frottement de faible coefficient

k

ralentit l'évolution du mouvement (ici la divergence), comme généralement pour ce type d'effet. Mais par ailleurs un frottement d'assez grand coefficient

k

change le signe de

Ω

τ

(en passant par l'infini) : le mouvement change de sens et devient convergent. Or, un frottement peut s'opposer au mouvement et le ralentir (en dissipant de l'énergie), mais il ne peut pas en changer le sens. Cela ne peut que renforcer les soupçons qui pèsent sur la modélisation.

3.c.

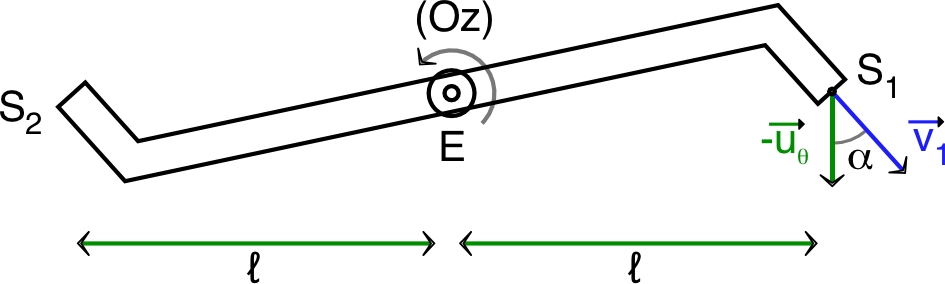
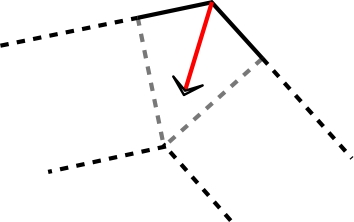
• Le liquide entrant à l'extrémité du tube a une vitesse

\overset{→}{V}

correspondant à une vitesse relative

\overset{→}{v}

de sens contraire, mais il n'acquiert cette vitesse que par interaction avec le tourniquet. Il n'apporte pas au système la quantité de mouvement correspondante puisqu'il ne l'acquiert qu'une fois intégré au système et interagissant avec ses autres parties.
• Le raisonnement précédent peut éventuellement s'appliquer, mais avec pour ce fluide entrant une vitesse nulle avant absorption :

$\left[\overset{→}{L}_O (t+dt)\right]-\left[\overset{→}{L}_O (t)+2 \,dm \:\overset{⟶}{OS} × \overset{→}{V} \right]=\overset{→}{0}$ ;
$\overset{→}{V}=\overset{→}{0}$ ; $J \:\ddot{θ}=0$ .

• Ceci correspond à une rotation uniforme, donc il est plus judicieux d'ajouter un frottement. On obtient ainsi une vitesse limite nulle et une constante de temps associée à la dissipation :

$J \:\ddot{θ}+k \:\dot{θ}=0$ ; $\displaystyle \frac{1}{τ}=\frac{k}{J}$ .

3.d.

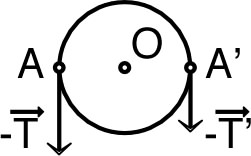
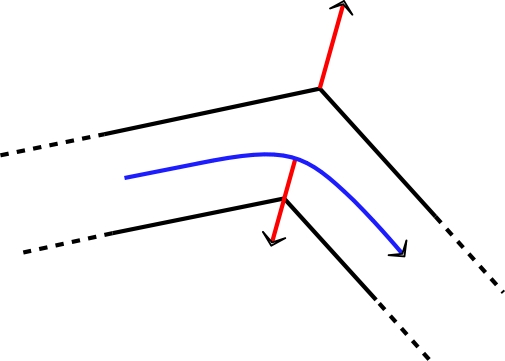
• Si on suppose le tube initialement vide (rempli d'air), la rotation du tourniquet (initialement immobile) pourrait commencer dès que du liquide entre à l'extrémité ; si une différence de pression peut faire entrer du liquide dans le tube (elle est indispensable pour provoquer sa mise en mouvement), elle peut aussi tendre à entrainer le coude en sens inverse (résultante des forces pressantes sur le coude comme dans la partie 2.a).
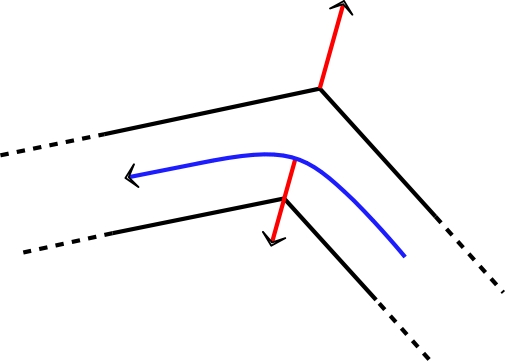
• Par contre, dès que du liquide passe le coude, l'interaction avec le tube dévie l'eau et l'action réciproque tend à mettre le tube en mouvement dans le sens anti-horaire (puisque le passage du coude dans l'autre sens ne modifie pas le sens des force résultantes sur le fluide et sur le tube).

dynSystemes_cor_Im/dynSystemes_cor_Im12.jpg

◊ remarque : cela se retrouve de même selon la mécanique des fluides.

• Contrairement à la situation observée pour le tourniquet en mode d'éjection (l'effet à l'extrémité n'était qu'une correction du second ordre), l'expérience montre que pour l'admission les deux effets se compensent généralement. Cette différence quantitative peut se comprendre dans la mesure où ce mode nécessite de mettre en mouvement le fluide en partant d'une vitesse nulle ; le terme correspondant est alors nettement plus important.

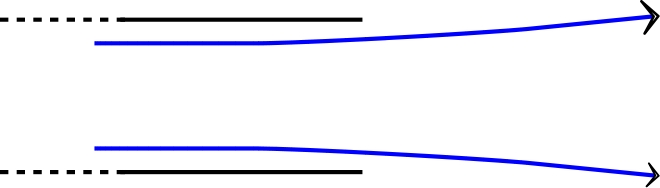
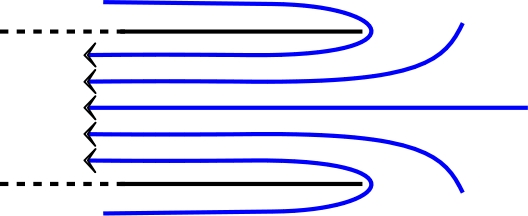
• La mécanique des fluides permet de préciser. En partant d'une vitesse nulle, le fluide est aspiré dans le tube en provenant de toute la périphérie (il n'y a pas de “jet”) et les ligne de courant ne décollent pas de la surface. En contournant le bord de façon plus abrupte, la dépression par effet Venturi au voisinage de l'extrémité est nettement plus marquée et permet ainsi l'importante accélération nécessaire.

dynSystemes_cor_Im/dynSystemes_cor_Im13.jpg

3.e.

• L'interaction au niveau de l'extrémité du tube peut dépendre notablement des lignes de courant, elles-mêmes dépendant de la forme du bord. Sans entrer dans le détail d'une description par la mécanique des fluides, on peut suggérer l'intervention d'un effet Venturi dans certains cas encore plus important : l'écoulement plus rapide au niveau de l'extrémité où les lignes de courant se resserrent cause une dépression supérieure et cet effet l'emporte un peu.

Théorème du viriel et masse non visible

• Pour les paires de points en interaction, on peut estimer l'ordre de grandeur des distances en moyenne

r_{ij}≈R

(entre

0

2 \:R

).
• La somme des produits des masses est :

∑ (m_i \: m_j ) ≈{\displaystyle \frac{N .(N-1)}{2} \, 〈 m_i 〉^2≈\frac{M^2}{2}}

.
• On obtient ainsi :

\displaystyle 〈 E_p 〉≈-\frac{𝒢 \:M^2}{2 \,R\,}

. De façon analogue :

2 〈 E_c 〉≈M 〈 v^2 〉

.
• Le théorème du viriel donne par conséquent :

\displaystyle 〈 v^2 〉≈\frac{𝒢 \:M^2}{2 \,R\,}

, permettant d'en déduire l'ordre de grandeur de la masse.
• En comparant au rapport masse/luminosité pour l'ensemble des observations astronomiques où ces données sont connues indépendamment, on peut déduire une estimation de la “masse lumineuse” du système étudié à partir de la luminosité observée. Cette masse est généralement très inférieure à celle déduite du théorème du viriel ; il semble donc qu'il existe une grande quantité de “masse sombre” (dont on ignore l'origine).

Glissement d'une chaînette sur un rebord

• On choisit un repérage dans le plan (constant) de la chaînette, avec l'origine à l'intersection des limites latérale et supérieure. On commence par étudier la limite de non glissement.

dynSystemes_cor_Im/dynSystemes_cor_Im14.jpg

• Une tranche

d𝓁

horizontale est soumise à la réaction du support compensant son poids :

dR=dP

, ce qui cause un frottement

df≤k \:dR =k \:λ \:d𝓁 \:g

. La portion horizontale est donc retenue par une tension

T_1≤k \:λ \:𝓁_1 \: g

. La portion verticale est soumise à son poids, compensé par une tension verticale

T_2=λ \:𝓁_2 \: g

.
• Pour une tranche

d𝓁=r \:dα

du rebord arrondi située à un angle

α

(mesuré à partir du dessus), le bilan des forces peut s'écrire :

$d\overset{→}{T}+d\overset{→}{R}+d\overset{→}{f}+d\overset{→}{P}=\overset{→}{0}$ ;
$d\overset{→}{T}=d[T(α) \: \overset{→}{u}_α ]=dT \;\overset{→}{u}_α-T \:dα \;\overset{→}{u}_r$ ;   $d\overset{→}{R}=dR \;\overset{→}{u}_r$ ;
$d\overset{→}{f}=-df \;\overset{→}{u}_α$ avec   $df≤k \:dR$ ;   $d\overset{→}{P}=λ \:r \:dα \:g .[-\cos(α) \; \overset{→}{u}_r+\sin(α) \; \overset{→}{u}_α ]$ ;
$-T \:dα+dR-\cos(α) \: λ \:r \:dα \:g=0$ ;   $dT-k \:dR+\sin(α) \: λ \:r \:dα \:g≤0$ .

• On en déduit :

$dT+\sin(α) \: λ \:r \:dα \:g≤k .[T \:dα+\cos(α) \: λ \:r \:dα \:g]$ ;
$\displaystyle \frac{dT}{dα}-k \:T≤λ \:r \:g .[k \;\cos(α)-\sin(α) ]$ .

• Une solution particulière pour l'égalité peut être cherchée de même forme que le second membre ; ceci peut s'écrire :

T_p=A \; \cos(α)+B \; \sin(α)

;

\displaystyle \frac{dT_p}{dα}-k \:T_p=(B-k \:A) \; \cos(α)-(A+k \:B) \; \sin(α)

.
• À cela on peut ajouter la solution de l'équation homogène, de la forme :

T_h=C \;\mathrm{e}^{k \,α}

; au total :

T=C \;\mathrm{e}^{k \,α}+A \; \cos(α)+B \; \sin(α)

mais cela ne change pas

\displaystyle \frac{dT}{dα}-k \:T

.
• En posant

Λ=λ \:r \:g

et en raisonnant avec

\displaystyle a=\frac{A}{Λ}

\displaystyle b=\frac{B}{Λ}

on est donc amené à résoudre l'équation :

(b-k \:a) \; \cos(α)-(a+k \:b) \; \sin(α)=k \; \cos(α)-\sin(α)

.
• L'inégalité devant être vérifiée pour tout

α∈\left[0 \:;\frac{π}{2}\right]

on peut considérer en particulier les deux cas limites :

b-k \:a=k

a+k \:b=1

. La résolution donne :

\displaystyle a=\frac{1-k^2}{1+k^2}

;

\displaystyle b=\frac{2 \,k}{1+k^2}

.
• On obtient ainsi au total :

\displaystyle T=C \;\mathrm{e}^{k \,α}+\frac{λ \:r \:g}{1+k^2} \: \left[(1-k^2 ) \; \cos(α)+2 \,k \; \sin(α)\right]

.
• On doit retrouver en particulier :

$\displaystyle T_1=T(0)=C+\frac{λ \:r \:g}{1+k^2} \: (1-k^2 )=k \:λ \:𝓁_1 \: g$ donnant : $\displaystyle C=k \:λ \:𝓁_1 \: g-\frac{λ \:r \:g}{1+k^2} \: (1-k^2 )$ ;
$\displaystyle T_2=T\left(\frac{π}{2}\right)=C \;\mathrm{e}^{k \,π/2}+\frac{λ \:r \:g}{1+k^2} \: 2 \,k=λ \:𝓁_2 \: g$ donnant : $\displaystyle C=\left(λ \:𝓁_2 \: g-\frac{λ \:r \:g}{1+k^2} \: 2 \,k\right) \;\mathrm{e}^{-k \,π/2}$ .

• Pour un arrondi donné, il y a donc glissement si

𝓁_1

est plus petit (et/ou

𝓁_2

plus grand) par rapport à la relation (où

λ

g

se simplifient) :

\displaystyle k \:𝓁_1-\frac{1-k^2}{1+k^2} \: r=\left(𝓁_2-\frac{2 k}{1+k^2} \; r\right) \;\mathrm{e}^{-k \,π/2}

.
• Pourvu que la chaînette ne soit pas trop courte, l'effet du frottement sur l'arrondi décrit par

λ \:r \:g

est relativement faible et peut souvent être négligé, par contre le coefficient

\mathrm{e}^{-k \,π/2}

caractérise une correction sur la transmission par le bord arrondi (et il est en fait indépendant de

r

) : le changement de direction fait que la tension, bien que tangentielle, contribue à augmenter le frottement car ses variations ont une composante perpendiculaire.
• Par exemple pour

k=0\text{,}2

(faible) ;

r=2 \:\mathrm{cm}

;

𝓁_2=20 \:\mathrm{cm}

; il faut au minimum

𝓁_1≈80 \:\mathrm{cm}

. Par contre avec

k=0\text{,}8

(fort) il suffit de

𝓁_1≈7 \:\mathrm{cm}