DYNAMIQUE - SYSTÈMES DE POINTS - exercices


A. EXERCICES DE BASE

Poussah

        • On colle la base d’un cylindre de rayon RR et de hauteur hh sur la face plane limitant une demi-sphère de même rayon RR , de façon que l’axe du cylindre passe par le centre de la sphère. Le cylindre est homogène de masse volumique ρ1ρ_1 et la demi-sphère est homogène de masse volumique ρ2ρ_2 .
        a) Calculer la hauteur hh du cylindre telle que le centre d’inertie de l’ensemble coïncide avec le centre de la sphère.
        ◊ indication : le centre d'inertie d'une demi-sphère se situe (par rapport au centre OO de la demi-sphère) à une distance  OG=38ROG=\frac{3}{8} R .
        b) Application numérique :  ρ1=0,8g.cm−3ρ_1=0\text{,}8 \;\mathrm{g.cm^{-3}} (bois)  ;  ρ2=11,3g.cm−3ρ_2=11\text{,}3 \;\mathrm{g.cm^{-3}} (plomb)  ;  R=1cmR=1 \;\mathrm{cm} .
        c) À quoi correspond cette condition du point de vue de l’équilibre ?


Équilibre

        a) Sur une table horizontale on pose des morceaux de sucre identiques les uns sur les autres. En les décrivant par une numérotation à partir du plus élevé : le premier tient en équilibre sur le second s’il dépasse de moins de la moitié de sa longueur ; à quelle condition l’ensemble des deux premiers tient-il en équilibre sur le troisième ?

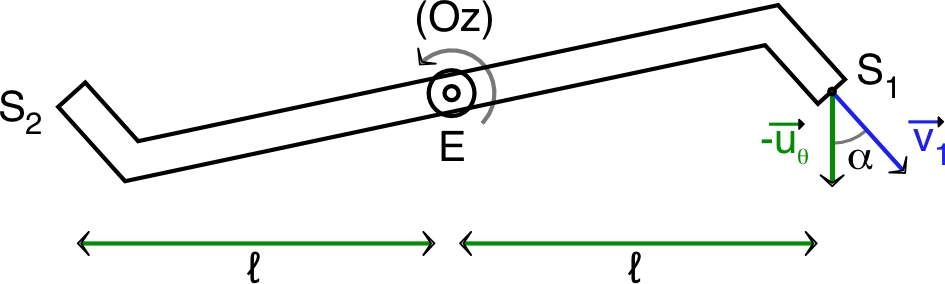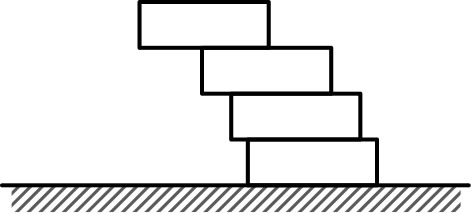
        b) En raisonnant de la même façon de proche en proche, quel nombre minimum de morceaux de sucre faut-il disposer sur la table pour que la projection du premier sur le plan horizontal soit entièrement extérieure au dernier morceau (qui est au contact de la table) ?
dynSystemes_ex_Im/dynSystemes_ex_Im2.jpg


Centre d’inertie

        • Une barque de masse mm flotte immobile sur l’eau ; le frottement de son fond plat sur l’eau est supposé négligeable quel que soit le mouvement. Le centre d’inertie de la barque est noté GG .
        • Dans cette barque se trouvent deux personnes représentées par des points matériels AA et BB de masses mAm_A et mBm_B . Les points AA , BB et GG sont initialement alignés, avec  AB=𝓁AB=𝓁 .
        • Les deux personnes permutent leurs positions ; calculer le déplacement  𝒹𝒹  du point GG .


Quantité de mouvement totale

        • Deux chariots de masses m1m_1 et m2m_2 , mobiles sur un banc à coussin d’air horizontal, comportent l’un un aimant et l’autre un morceau de fer. On les lâche à la distance  𝒹𝒹  l’un de l’autre avec des vitesses initiales nulles. En supposant qu’après le choc ils restent solidaires, quelle sera la vitesse de l’ensemble ?


Énergie mécanique

        • Deux points matériels de masses m1m_1 et m2m_2 glissent sans frottement sur un axe horizontal OxOx ; leurs positions sont repérées par x1x_1 et x2x_2 . Ces deux points sont liés par un ressort de raideur kk , de masse négligeable et de longueur au repos 𝓁0𝓁_0 . On écarte les deux points de leur position d’équilibre et on les lâche avec une vitesse initiale nulle.

1.     • Écrire l’équation différentielle du mouvement de chacun des points.

2.     • En déduire l’équation du mouvement du barycentre GG ; quel résultat retrouve-t-on ainsi ?

3.     • En multipliant la première équation par x˙1\dot{x}_1 et la seconde par x˙2\dot{x}_2 , mettre en évidence la conservation de l’énergie mécanique EmE_m du système et donner son expression.

4.     • En multipliant la première équation par m2m_2 et la seconde par m1m_1 , montrer que par différence on en déduit une équation différentielle simple sur la variable  ξ= x2−x1 −𝓁0 ξ=x_2-x_1-𝓁_0 .  En déduire la période TT des oscillations du système.


Travail des forces intérieures et changement de référentiel

        • On considère un changement de référentiel associé à une translation de l'origine à la vitesse v→O\overset{→}{v}_O et à une rotation des vecteurs de base à la vitesse angulaire ω→ \overset{→}{ω} par rapport à OO .
        • Montrer que, pour un système de points matériels, la puissance et le travail des forces intérieures ne sont pas modifiés par le changement de référentiel.


Machine d'Atwood

1.     • On considère une “machine d'Atwood” (ci-dessous à gauche) constituée de deux blocs, représentés par des points matériels MM et M′M' (de masses mm et m′m' ), reliés par un fil “idéal” (inextensible et de masse négligeable) passant par une poulie de rayon RR et de moment d'inertie JJ .
        • En raisonnant (pour la poulie) d'après le moment cinétique, établir l'équation différentielle décrivant le mouvement du système.

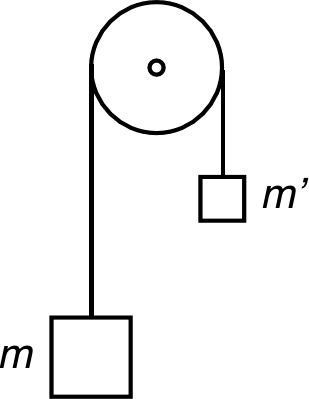dynSystemes_ex_Im/dynSystemes_ex_Im1.jpg
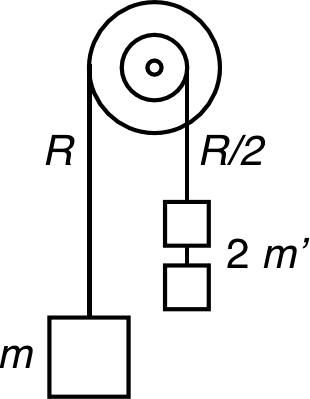 dynSystemes_ex_Im/dynSystemes_ex_Im4.jpg

2.     • En raisonnant d'après l'énergie mécanique, établir l'équation différentielle du mouvement pour un système à poulie double (ci-dessus à droite).


B. EXERCICES D'APPROFONDISSEMENT

Travail des forces d'inertie et référentiel barycentrique

        • Montrer que, pour un système de points matériels, la puissance et le travail des forces d'inertie sont nuls dans le référentiel barycentrique ℛ*ℛ^* .


Centre d’inertie

1.     • On considère une tige mince homogène en forme de demi-cercle de rayon RR . Déterminer la position du centre d’inertie par rapport au diamètre qui limite le demi-cercle.

2.     • On considère un demi-cylindre homogène de rayon RR . Déterminer la position du centre d’inertie par rapport au plan méridien qui limite le demi-cylindre.


Théorèmes de Kœnig

        • L’intérêt du référentiel barycentrique est de séparer l’étude du mouvement d’un système en une translation d’ensemble (déplacement de GG ) et une rotation-déformation par rapport à GG . Les théorèmes de Kœnig consistent à exprimer L→O\overset{→}{L}_O et EcE_c (dans un référentiel ℛℛ galiléen) en fonction de L→G*\overset{→}{L}{}_G^* et Ec*E_c^* (dans le référentiel ℛ*ℛ^* barycentrique).

1.     a) Dans ℛℛ galiléen, montrer que le changement de référence correspond à :  L→O=OG⟶×p→+L→G\overset{→}{L}_O=\overset{⟶}{OG} × \overset{→}{p}+\overset{→}{L}_G .
        b) Montrer que par ailleurs :  L→G=L→G*\overset{→}{L}_G=\overset{→}{L}{}_G^*  et en déduire finalement :  L→O=OG⟶×p→+L→G*\overset{→}{L}_O=\overset{⟶}{OG} × \overset{→}{p}+\overset{→}{L}{}_G^* .

2.     • D’une façon analogue, montrer que :  Ec=12(∑mi)vG2+Ec*E_c=\frac{1}{2} (∑ m_i ) \: v_G^{\:2}+E_c^* .


Énergie cinétique et moment cinétique

        • Compte tenu des proportions, on assimile la Terre et la Lune à deux points matériels de masses m1m_1 et m2m_2 . La distance Terre-Lune, notée 𝓁𝓁 , est considérée comme constante : on admet que ces deux points décrivent des orbites circulaires autour de leur barycentre GG à la vitesse angulaire constante ωω (mesurée par rapport à des directions fixes d’un référentiel galiléen).
        • Le barycentre GG décrit autour du Soleil, supposé fixe à l’origine OO , une orbite considérée comme circulaire de rayon AA , à la vitesse angulaire constante ΩΩ . Les deux mouvements sont supposés coplanaires et les deux rotations ont lieu dans le même sens.

1.     • Calculer l’énergie cinétique du système Terre-Lune dans le référentiel “fixe” d’origine OO .

2.     • Calculer le moment cinétique en OO du système Terre-Lune dans le référentiel “fixe” d’origine OO .


Tourniquet de Mach-Feynman

        • On considère un tourniquet dont le tube coudé mobile, horizontal, de section ss , peut tourner autour de l'axe vertical (Oz)(Oz) .

dynSystemes_ex_Im/dynSystemes_ex_Im3.jpg

        ◊ remarque : pour mieux mettre en évidence les aspects importants du raisonnement, on peut calculer plus simplement le moment cinétique en négligeant le diamètre du tube en comparaison de sa longueur.

1.     • Le tourniquet, placé dans l'air, est alimenté en eau par une entrée EE située sur un tube vertical selon (Oz)(Oz) , muni d'un raccord rotatif étanche. L'eau est éjectée par chacune des deux extrémités symétriques S1S_1 et S2S_2 avec un débit DD .
        ◊ remarque : un tel dispositif devrait être étudié à l'aide de la mécanique des fluides ; on suppose que les raisonnements utilisés ici donnent une bonne approximation.
        a) En négligeant tous les frottements, établir un bilan de moment cinétique et en déduire l'équation du mouvement du tourniquet.
        b) Bien que l'eau soit en mouvement dans le tube, justifier qu'on peut décrire la rotation du dispositif à l'aide d'un moment d'inertie.
        c) Résoudre l'équation et commenter le mouvement.
        d) Le raisonnement utilisé semble considérer le mouvement du tourniquet comme causé par le liquide éjecté ; c'est seulement parce que le bilan est plus facile ainsi. Préciser les causes de ce mouvement.

2.     a) Le tourniquet est maintenant placé dans l'eau. Discuter dans quelle mesure le raisonnement précédent peut encore s'appliquer.
        b) Ajouter un effet de frottement fluide visqueux et commenter.

3.     a) Le tourniquet placé dans l'eau est maintenant utilisé en mode d'admission. Exprimer l'équation obtenue en appliquant le raisonnement précédent, sans frottement, en changeant simplement le sens de la vitesse relative d'éjection. Commenter le mouvement en résultant.
        b) Ajouter un effet de frottement fluide visqueux et commenter.
        c) Expérimentalement, dans la plupart des cas, un tel dispositif en mode d'admission reste immobile s'il l'est initialement (des vidéos se trouvent sur internet : rechercher “sprinkler”). En outre, si on essaye de le lancer manuellement, il s'arrête assez rapidement (à cause des frottements). Proposer une modification du modèle permettant de décrire cela.
        d) Le raisonnement utilisé est basé sur un bilan car il est plus facile ainsi. Préciser les interactions locales qui pourraient a priori causer un mouvement.
        e) Quelques dispositifs montrent un comportement expérimental différent : le mouvement inverse en mode d'admission existe et est analogue, mais la vitesse limite est nettement plus faible. Proposer une interprétation.


Théorème du viriel et masse non visible

        • On souhaite appliquer le théorème du viriel à un amas sphérique de NN galaxies, de rayon RR , de masse totale MM .
        • La vitesse quadratique moyenne peut être estimée d'après l'effet Doppler observé pour la lumière reçue. L'observation lumineuse fournit aussi une estimation du rayon.
        • Montrer que le théorème du viriel donne une relation permettant de calculer la masse :  〈v2〉≈𝒢M2R\displaystyle 〈v^2 〉≈\frac{𝒢 \:M}{2 \,R} .


Glissement d'une chaînette sur un rebord

        • Une Chaînette de longueur 𝓁𝓁 , inextensible et sans raideur, est placée initialement immobile “à cheval” sur un rebord d'une table, selon la perpendiculaire au rebord. La limite du bord arrondi est modélisée par une forme circulaire de rayon rr . On note λλ la masse linéique et kk le coefficient de frottement statique.
        • Établir les conditions de non glissement sous l'effet de la pesanteur.