◊ remarque : pour visualiser correctement les variations brutales de , il faut utiliser un signal de fréquence assez faible.
| ◊ |
des courants d'entrée, ou “courants de polarisation”, et nuls (résistances d'entrée infinies) ; | ||
| ◊ | une différence de potentiel entre les deux
entrées
:
|
||
| ◊ | une résistance de sortie :
|
||
| ◊ | une tension de sortie en mode saturé (où est la tension d'alimentation). |
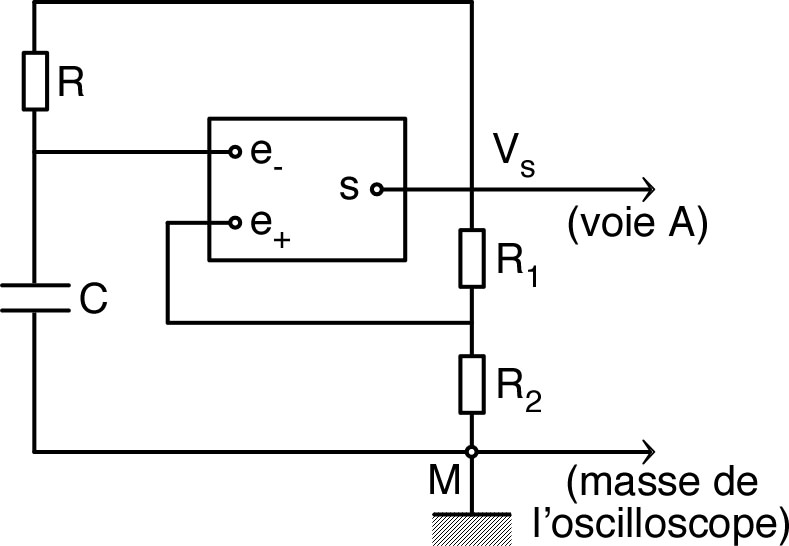
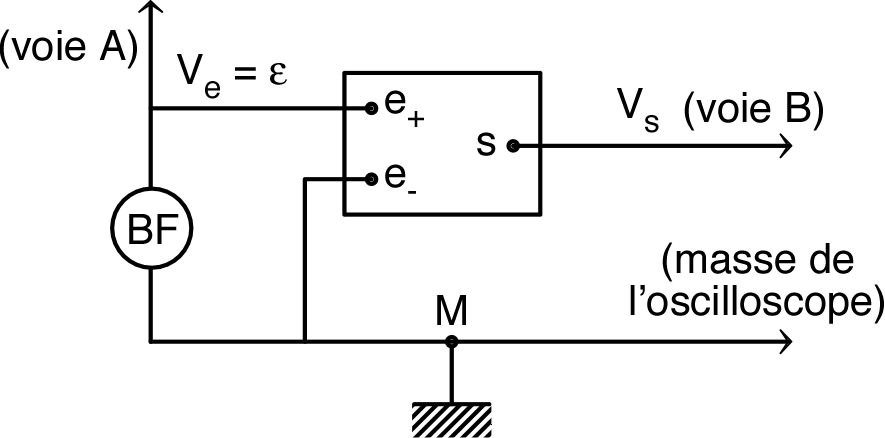
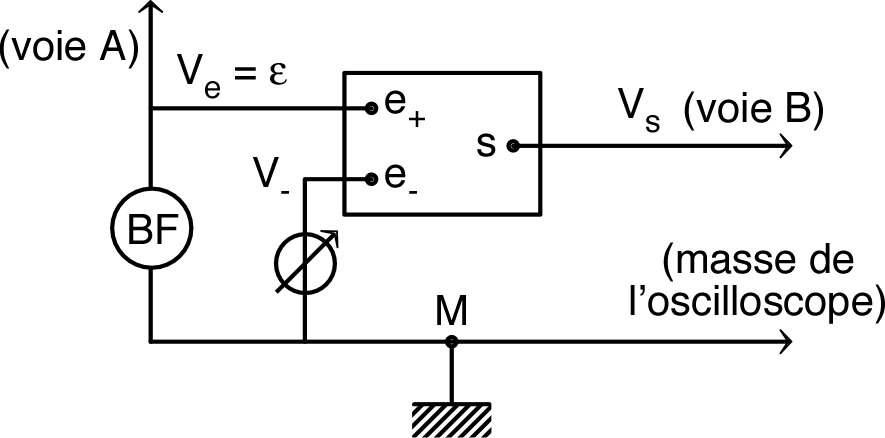
| • Réaliser le montage ci-contre, branché
en entrée sur un générateur “basse fréquence” (BF) en mode
sinusoïdal. ◊ remarque : pour visualiser correctement les variations brutales de , il faut utiliser un signal de fréquence assez faible. |
 |
|
en mode linéaire (
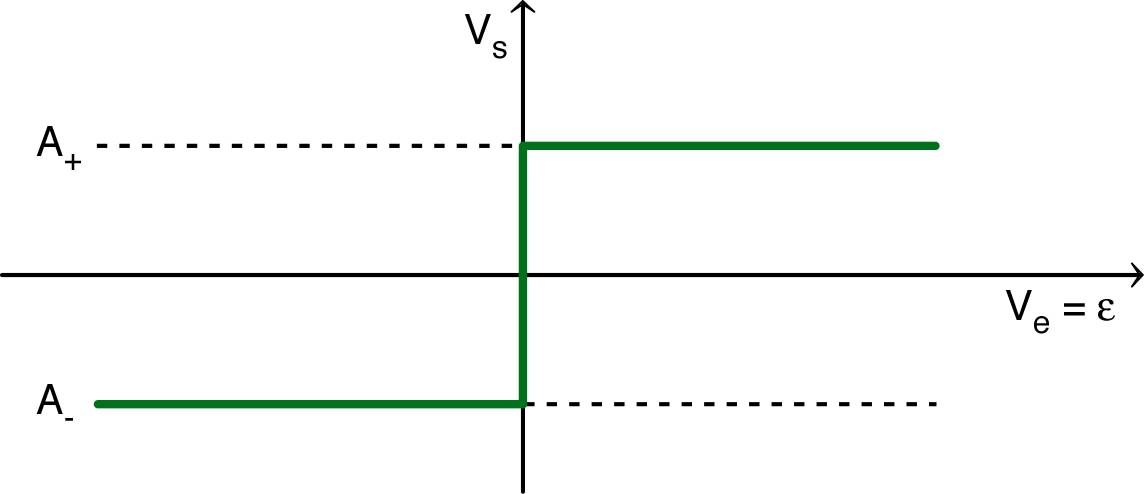
) ; et du signe de en mode “saturé positif” ( ) ; et du signe de en mode “saturé négatif” ( ). |
| ◊ rappel : si on ne dispose que d’une alimentation continue non réglable, on peut utiliser un rhéostat pour la transformer en alimentation continue réglable à l’aide d’un montage “diviseur de tension”. | 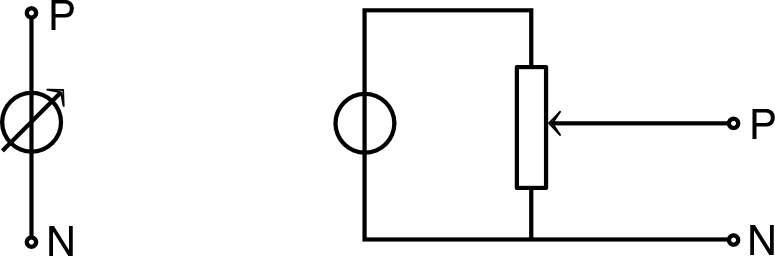 |
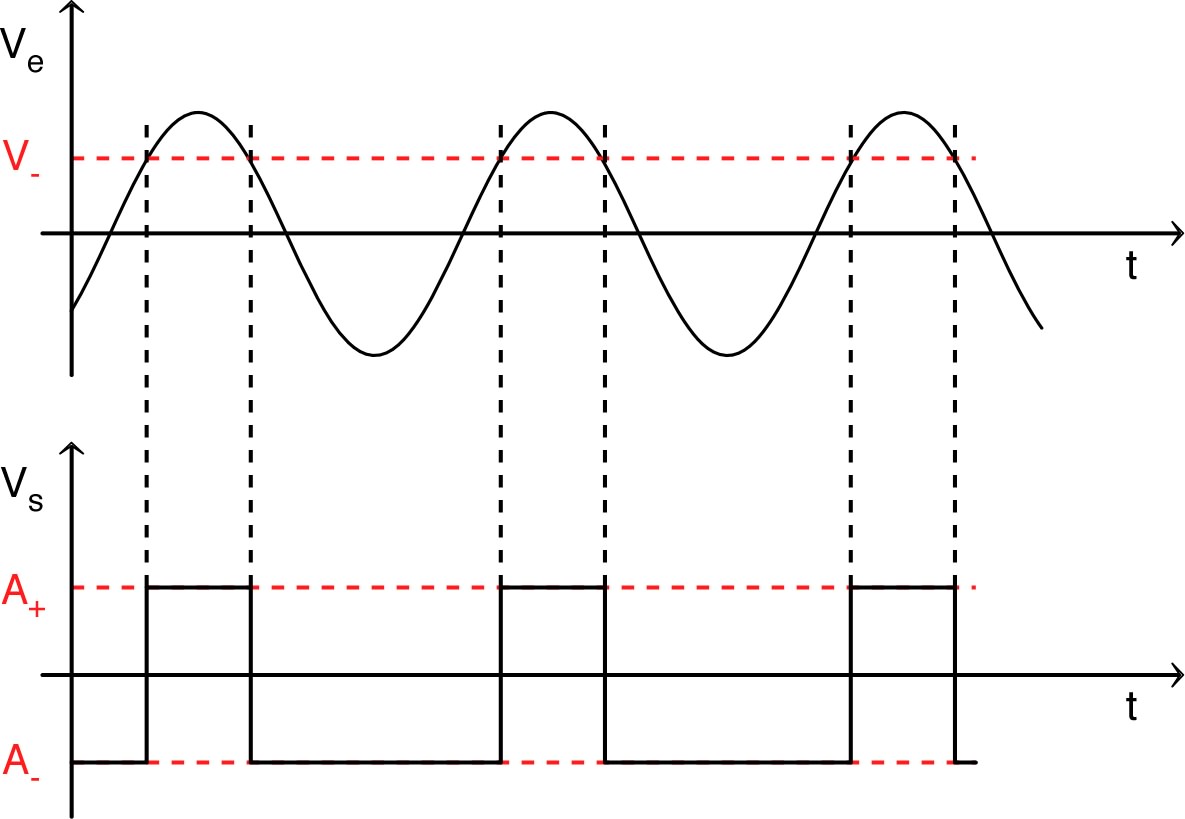
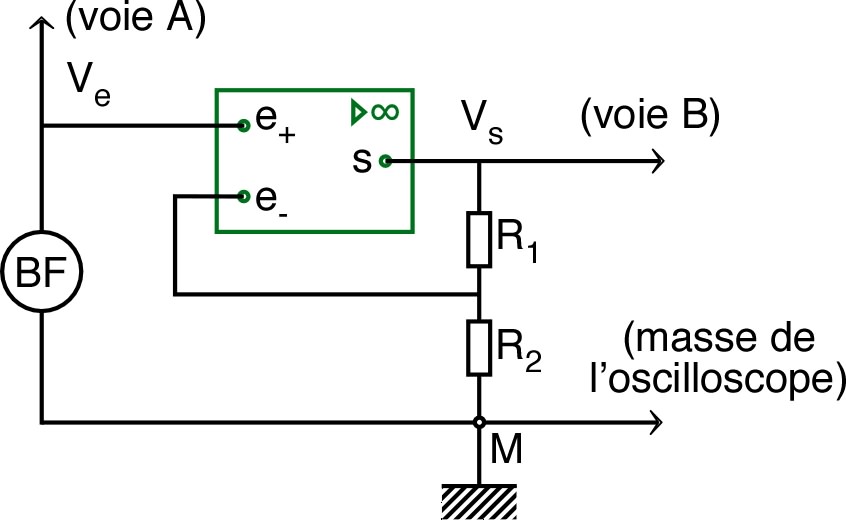
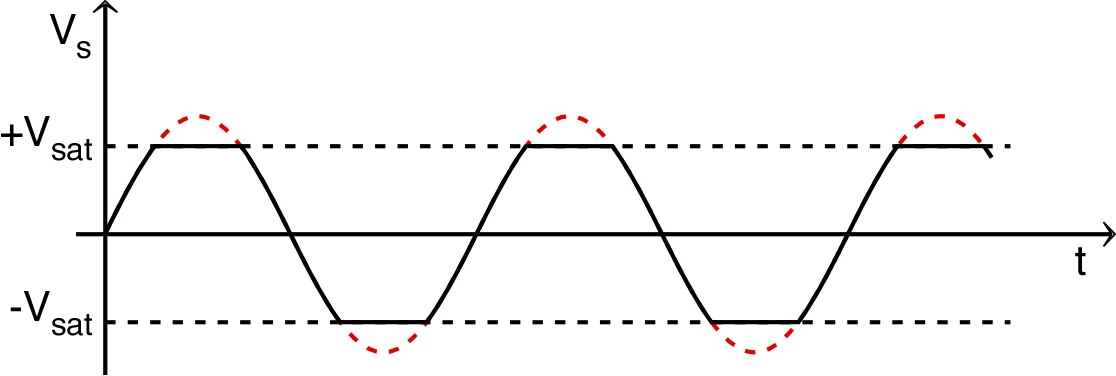
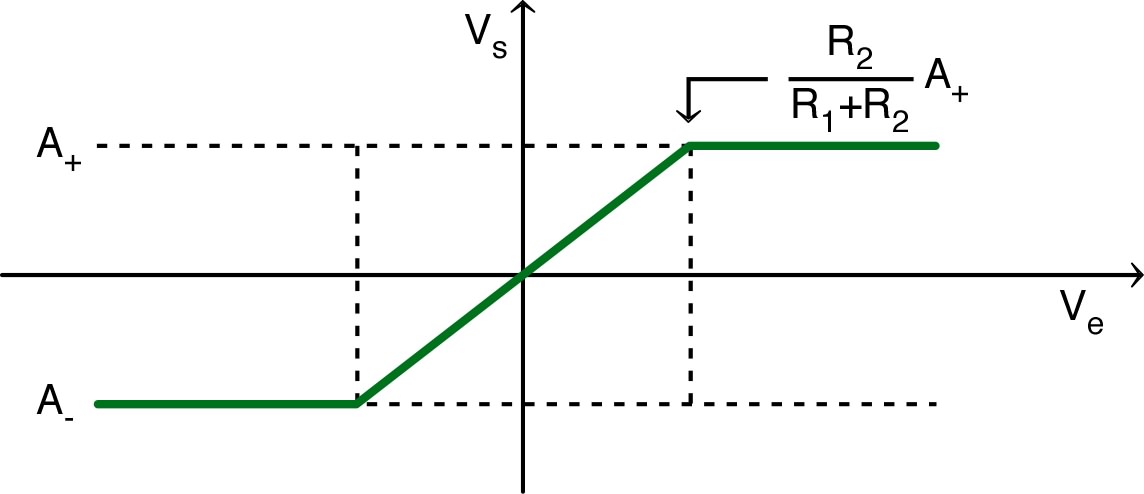
| pour ; pour . |
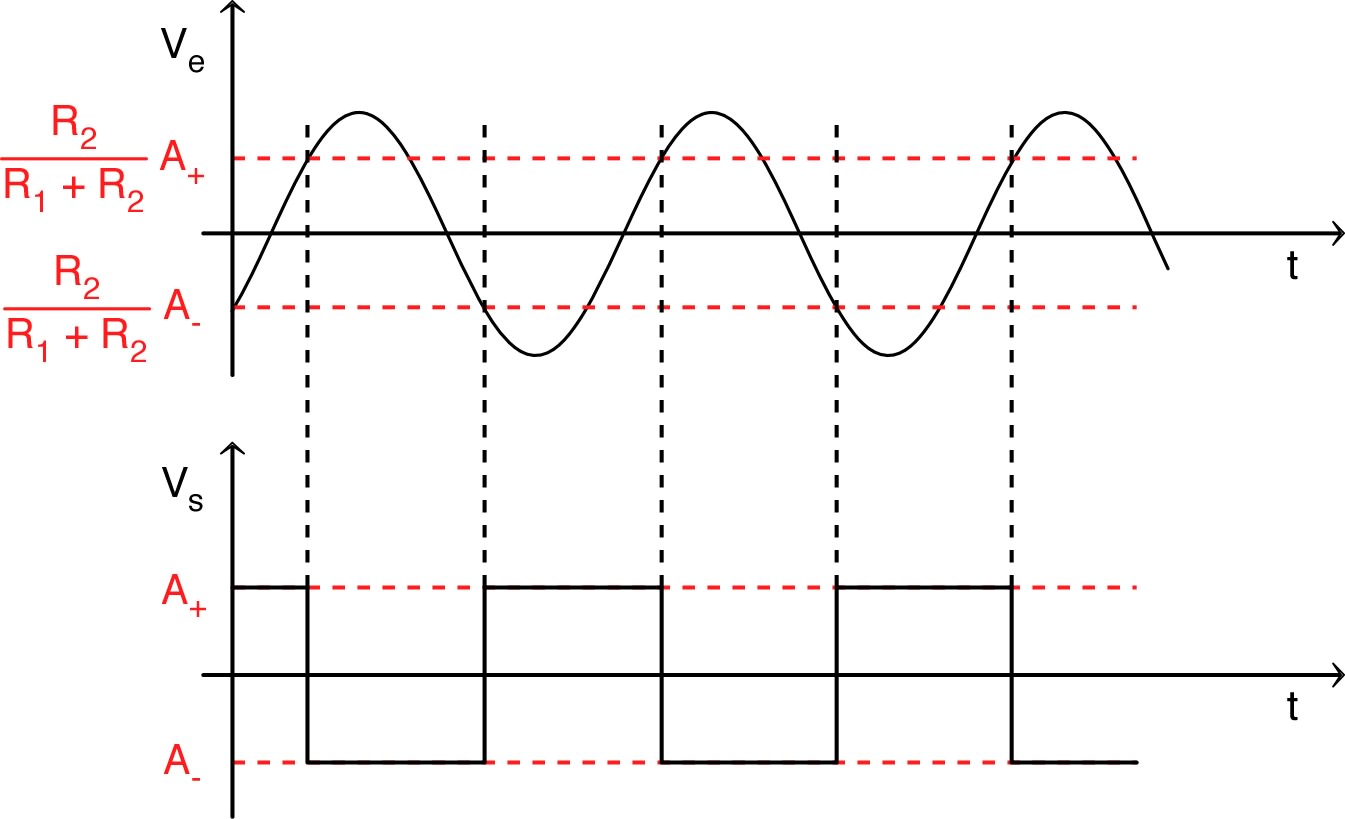
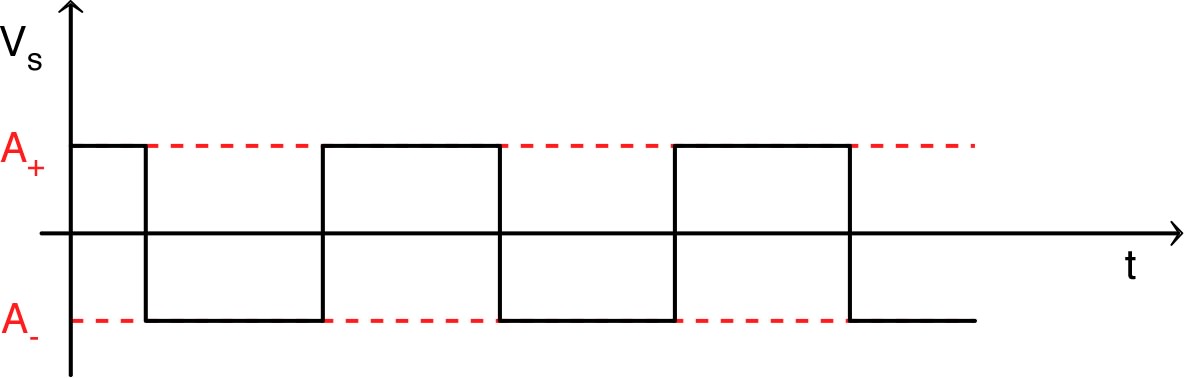
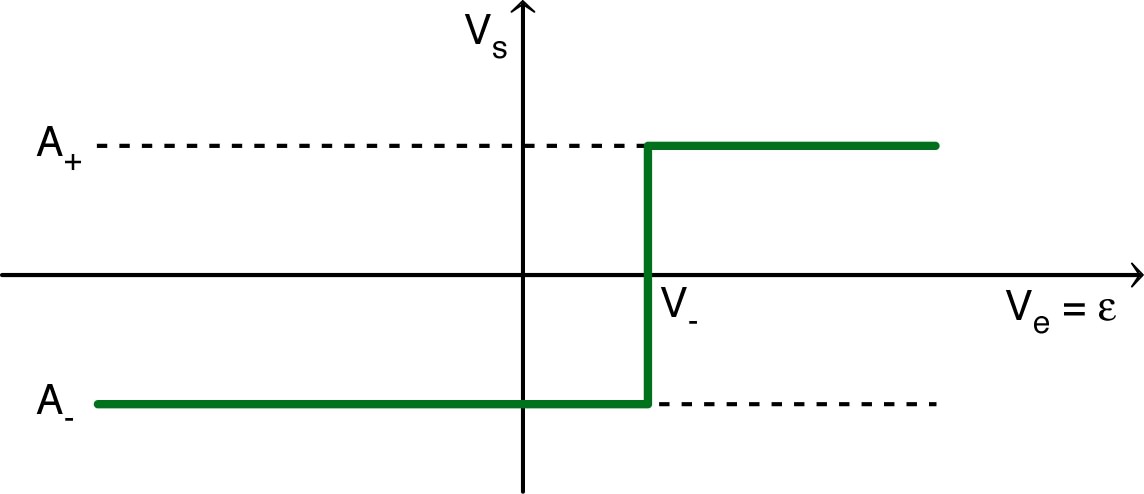
5.1. Caractéristique “statique”• En intervertissant simplement les entrées et , réaliser le montage “comparateur à hystérésis” (inverseur), branché en entrée sur un générateur sinusoïdal (avec, de même que précédemment, une amplitude suffisante du signal d’entrée). |
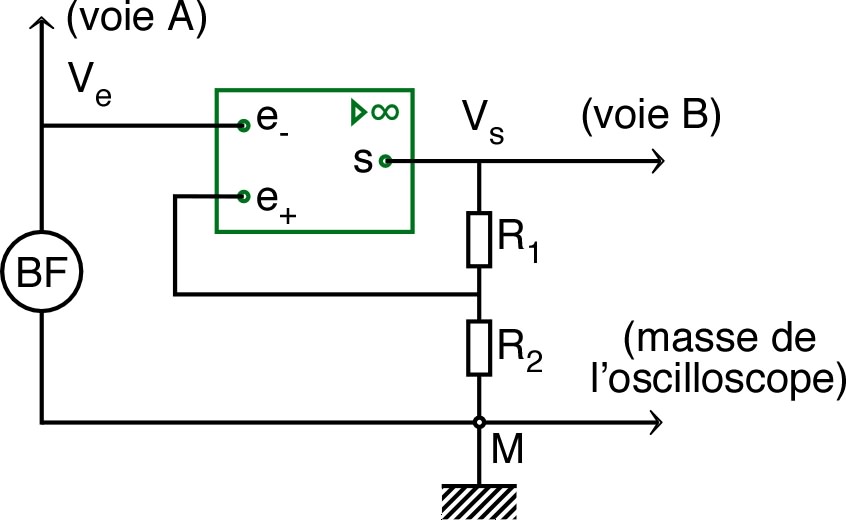 |
|
pour
(mode linéaire) ; pour ; pour ; |
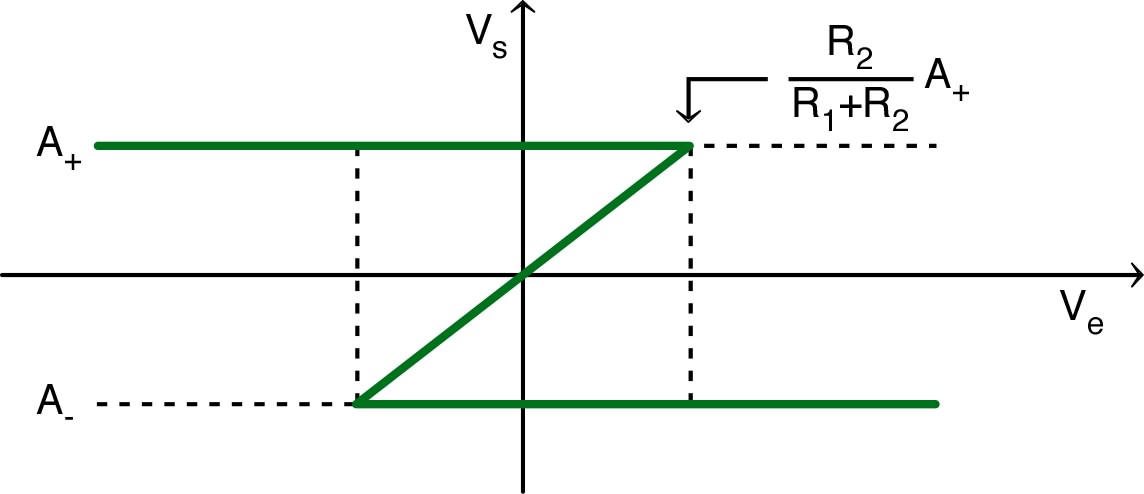
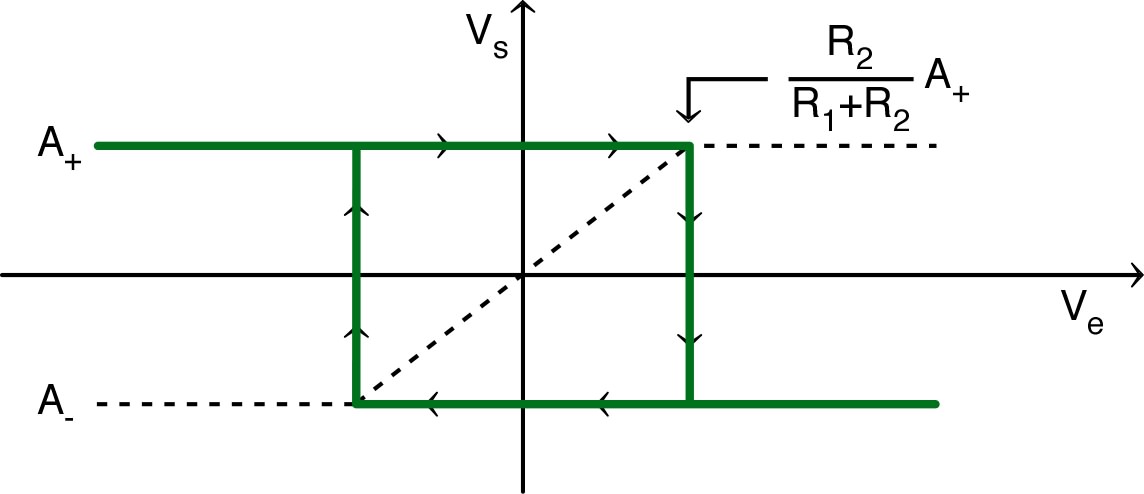
| ◊ |
le segment central n’est jamais parcouru : il correspond à un “équilibre” instable du montage ; |
| ◊ | les segments qui décrivent les solutions avec saturation pour ne sont parcourus chacun que pour l’un des sens de variation de ; |
| ◊ | il apparaît une “bascule” rapide de pour passer d’une saturation à l’autre. |
| ◊ |
en mode linéaire : généralement négligeable ( ) ; |
| ◊ | en mode saturé : sature avec le signe de puisque . |
| ◊ |
à un équilibre stable pour l’amplificateur non-inverseur : un signal parasite qui augmente , donc aussi , provoque ainsi une augmentation de , qui provoque une augmentation de ( fois plus grande), qui provoque une augmentation de , donc une diminution de , ce qui compense le parasite ; |
| ◊ | à un équilibre instable pour le comparateur à hystérésis : un signal parasite qui augmente , donc aussi , provoque ainsi une diminution de , qui provoque une diminution de ( fois plus grande), qui provoque une diminution de , donc une diminution de , ce qui accentue le parasite d’un facteur et provoque la saturation (le fonctionnement “linéaire” est alors inobservable...). |