AMPLIFICATEUR OPÉRATIONNEL “IDÉAL” EN MODE “SATURÉ” - corrigé du TP


2. Caractéristique des modes linéaire et “saturé”

• En attente de données fournies par les étudiants...

3. Montage “comparateur”

• En attende de données fournies par les étudiants...

4. Montage amplificateur non-inverseur en mode “saturé”

• Le montage est réalisé avec un générateur B.F. réglé sur la fréquence  N=995,3±5,2HzN=\text{995,3}±\text{5,2} \:\mathrm{Hz}  (mesurée avec le fréquencemètre incorporé). Les signaux enregistrés sur l'ordinateur donnent alors  N=1017,6±5,1HzN=\text{1017,6}±\text{5,1} \:\mathrm{Hz} .  L'étude des fichiers informatiques laisse par contre soupçonner que les données ont été mal traduites de kibi\mathrm{kibi} (1024) en kilo\mathrm{kilo} (1000) ; la fréquence serait ainsi  N=993,8±5,0HzN=\text{993,8}±\text{5,0} \:\mathrm{Hz}  tout à fait compatible.

• Les résistances utilisées sont  R1=81,58±0,43kΩR_1=\text{81,58}±\text{0,43} \:\mathrm{kΩ}  et  R2=32,33±0,18kΩR_2=\text{32,33}±\text{0,18} \:\mathrm{kΩ} .

• On peut considérer en mode linéaire :  Ve=Ve+=Ve−V_e=V_{e_{+}}=V_{e_{-}}  ;  or, puisque  I−=0I_{-}=0 ,  le branchement en sortie est un pont diviseur de tension :  Ve−=R2R1+R2Vs\displaystyle V_{e_{-}}=\frac{R_2}{R_1+R_2} \: V_s  ;  inversement :  Vs=R1+R2R2Ve\displaystyle V_s=\frac{R_1+R_2}{R_2} \: V_e .

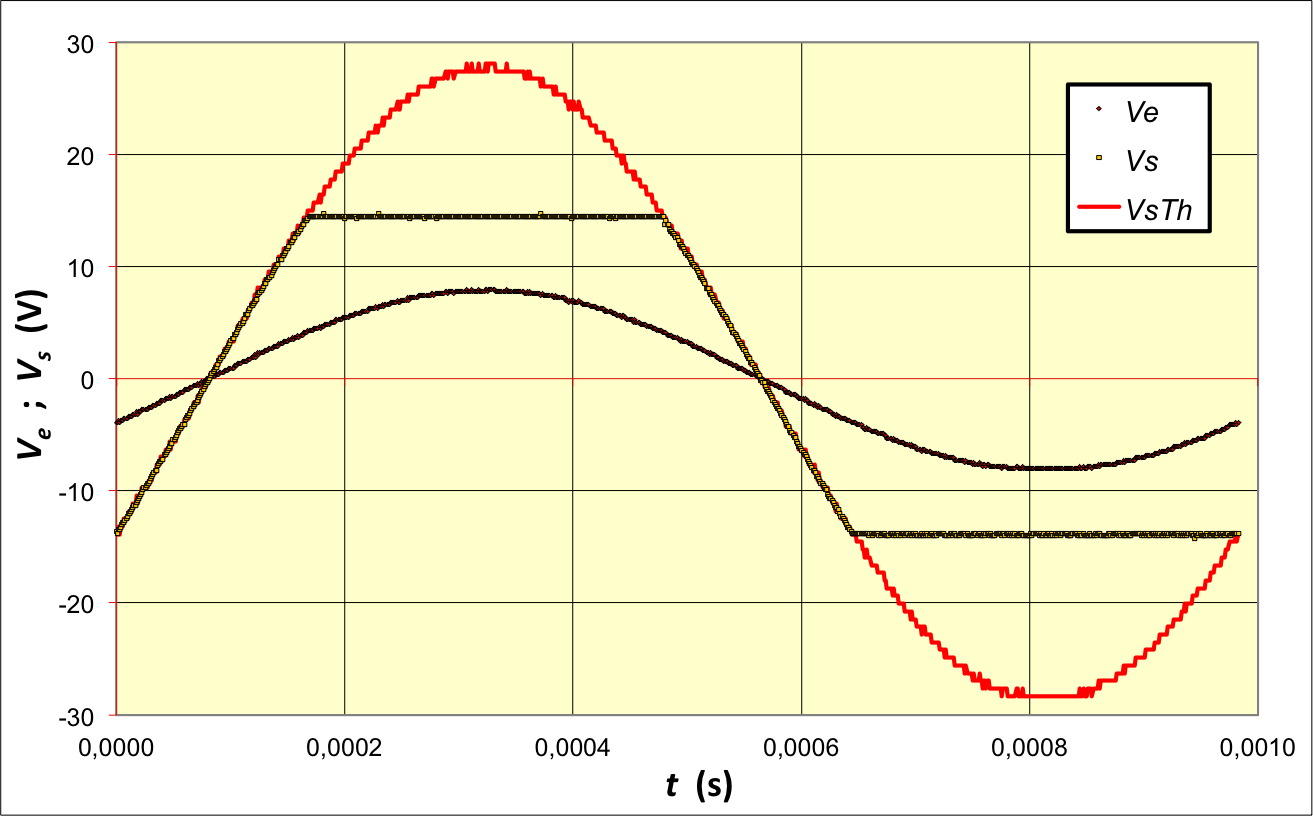
Les mesures montrent un signal  VsV_s  correctement décrit par ce modèle, mais seulement dans les limites d'un effet de saturation.

AOidsat_corTP_Im/ampliNI1.png

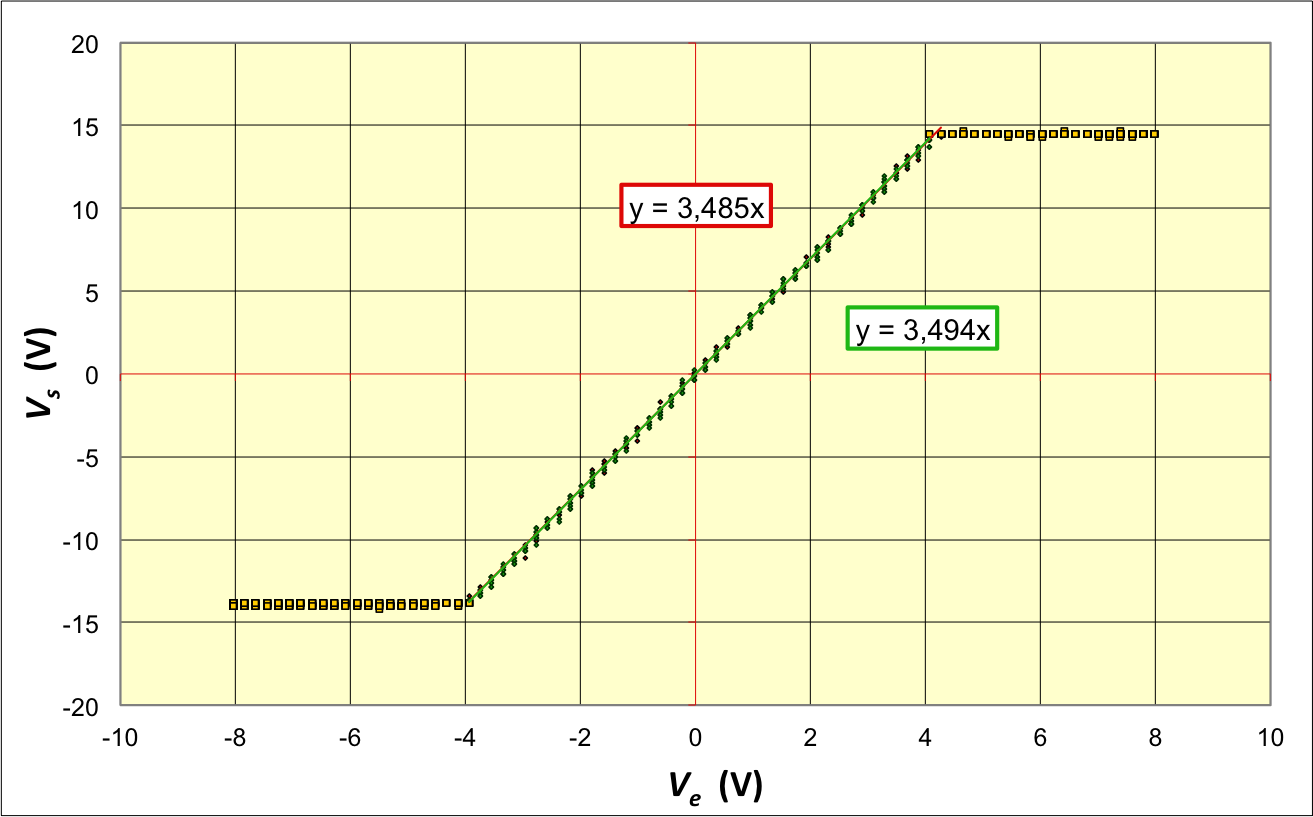
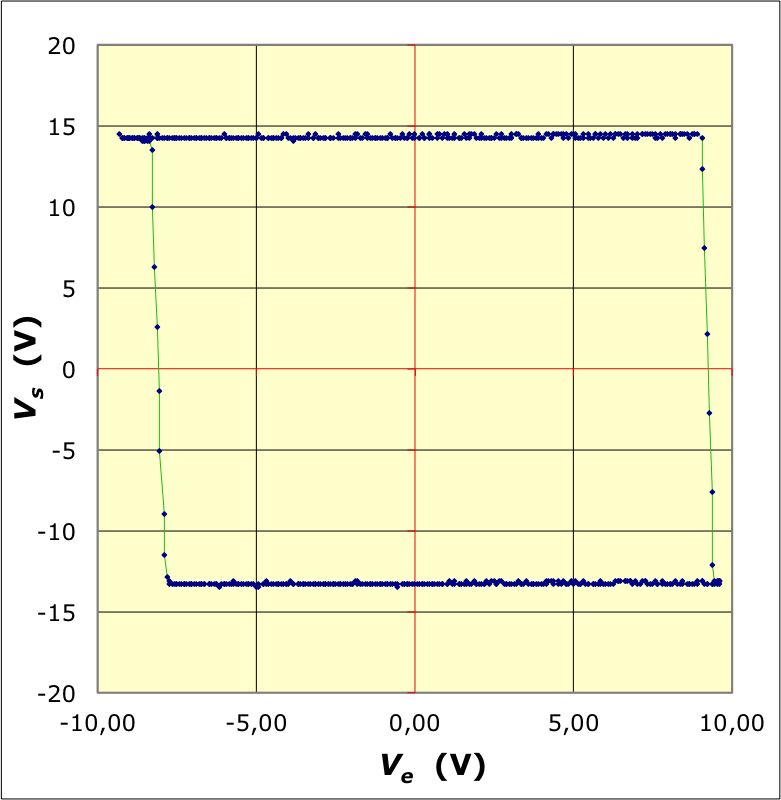
• La représentation en mode “XY” donne la caractéristique complète (incluant la saturation).

La pente de la partie linéaire correspond à un gain  G=3,49±0,01G=\text{3,49}±\text{0,01}  ;  le modèle proposé est tout à fait compatible :  R1+R2R2=3,523±0,027\displaystyle \frac{R_1+R_2}{R_2} =\text{3,523}±\text{0,027} .

AOidsat_corTP_Im/ampliNI2.png

La saturation est observée pour :  vs=Vsat+=14,50±0,27Vv_s=V_{{sat}_{+}}=\text{14,50}±\text{0,27} \:\mathrm{V}  ;  vs=Vsat−=−13,91±0,27Vv_s=V_{{sat}_{-}}=-\text{13,91}±\text{0,27} \:\mathrm{V} .  Ceci est à comparer aux tensions d'alimentation :  A+=15,08±0,08VA_{+}=\text{15,08}±\text{0,08} \:\mathrm{V}  ;  A−=−15,23±0,08VA_{-}=-\text{15,23}±\text{0,08} \:\mathrm{V} .  On observe une très légère dissymétrie, mais raisonnablement compatible avec les incertitudes de mesure.

◊ remarque : on constate que la saturation intervient (en valeur absolue) environ  1V1 \:\mathrm{V}  au dessous de la tension d'alimentation ; ceci donne bien l'ordre de grandeur, mais montre une dépendance par rapport aux détails des circuits intégrés des A.O..

5. Montage “comparateur à hystérésis”

5.1. Caractéristique “statique”

• Le montage est réalisé avec un générateur B.F. réglé sur une fréquence plus faible (pour observer les bascules de la saturation)  N=44,34±0,25HzN=\text{44,34}±\text{0,25} \:\mathrm{Hz}  (mesurée avec le fréquencemètre incorporé). Les signaux enregistrés sur l'ordinateur donnent  N=44,13±0,25HzN=\text{44,13}±\text{0,25} \:\mathrm{Hz}  (après correction de l'échelle de temps).

• Les résistances utilisées sont  R1=33,64±0,19kΩR_1=\text{33,64}±\text{0,19} \:\mathrm{kΩ}  et  R2=47,93±0,26kΩR_2=\text{47,93}±\text{0,26} \:\mathrm{kΩ} .

• La démonstration théorique précédente pour le mode linéaire est toujours valable puisqu'elle utilise  ε=0ε=0  qui n'est pas modifié par la permutation des deux bornes :  Vs=R1+R2R2Ve\displaystyle V_s=\frac{R_1+R_2}{R_2} \: V_e   pour   R2R1+R2A−≤Ve≤R2R1+R2A+\displaystyle \frac{R_2}{R_1+R_2} \: A_{-}≤V_e≤\frac{R_2}{R_1+R_2} \: A_{+} .

Pour le mode saturé  Vs=A+V_s=A_{+} ,  on doit considérer  ε≥0ε≥0  car de même signe (μ>0μ>0 ). Ceci correspond à :  Ve≤V+=R2R1+R2Vs\displaystyle V_e≤V_{+}=\frac{R_2}{R_1+R_2} \: V_s  donc  Ve≤R2R1+R2A+\displaystyle V_e≤\frac{R_2}{R_1+R_2} \: A_{+} .

De même pour  Vs=A−V_s=A_{-} ,  on doit considérer  ε≤0ε≤0  car de même signe (μ>0μ>0 ). Ceci correspond à :  Ve≥V+=R2R1+R2Vs\displaystyle V_e≥V_{+}=\frac{R_2}{R_1+R_2} \: V_s  donc  Ve≥R2R1+R2A−\displaystyle V_e≥\frac{R_2}{R_1+R_2} \: A_{-} .

5.2. Caractéristique “dynamique”

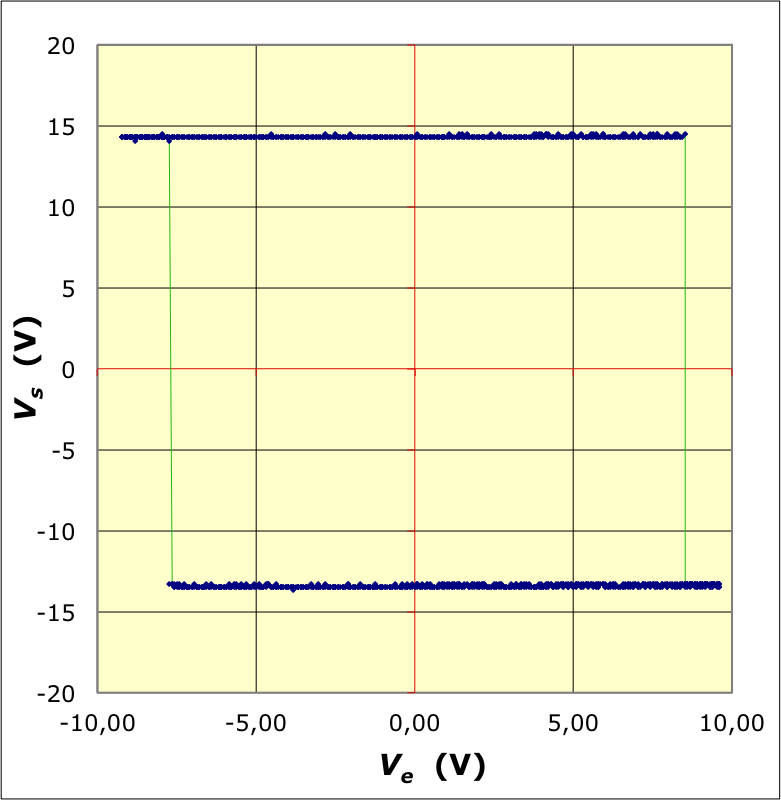
• On vérifie expérimentalement, en mode “XY”, que la caractéristique observée est du type indiqué (l'énoncé indique le raisonnement justificatif).

◊ remarque : on choisit ici un signal triangulaire pour répartir plus régulièrement les points mesurés.

AOidsat_corTP_Im/compar1.png

• Les tensions d'alimentation sont  A+=14,82±0,08VA_{+}=\text{14,82}±\text{0,08} \:\mathrm{V}   et   A−=−14,47±0,08VA_{-}=-\text{14,47}±\text{0,08} \:\mathrm{V} .  La sortie débite un courant  Is=VsR1+R2≈±180μA\displaystyle I_s=\frac{V_s}{R_1+R_2}≈±180 \:\mathrm{μA}  et la chute de tension dans la résistance de sortie est  ρIs≈±60mVρ \:I_s≈±60 \:\mathrm{mV}  avec  ρ≈350Ωρ≈350 \:\mathrm{Ω}  (pour de nombreux A.O.).

On constate les saturations pour  Vsat+=14,3±0,5VV_{sat+}=\text{14,3}±\text{0,5} \:\mathrm{V}   et   Vsat−=−13,4±0,5VV_{sat-}=-\text{13,4}±\text{0,5} \:\mathrm{V} .  Le décalage par rapport aux tensions d'alimentation est de l'ordre de grandeur de 1V1 \:\mathrm{V}  ;  sa cause, non expliquée par la résistance de sortie, est liée de façon non évidente à la structure interne de l'A.O. réel (non idéal).

• Les vérifications de l'influence de R1R_1 et R2R_2 sur les tensions de “bascule” ont été faites visuellement par les étudiants : ils n'ont pas donné plusieurs séries de mesures correspondantes.

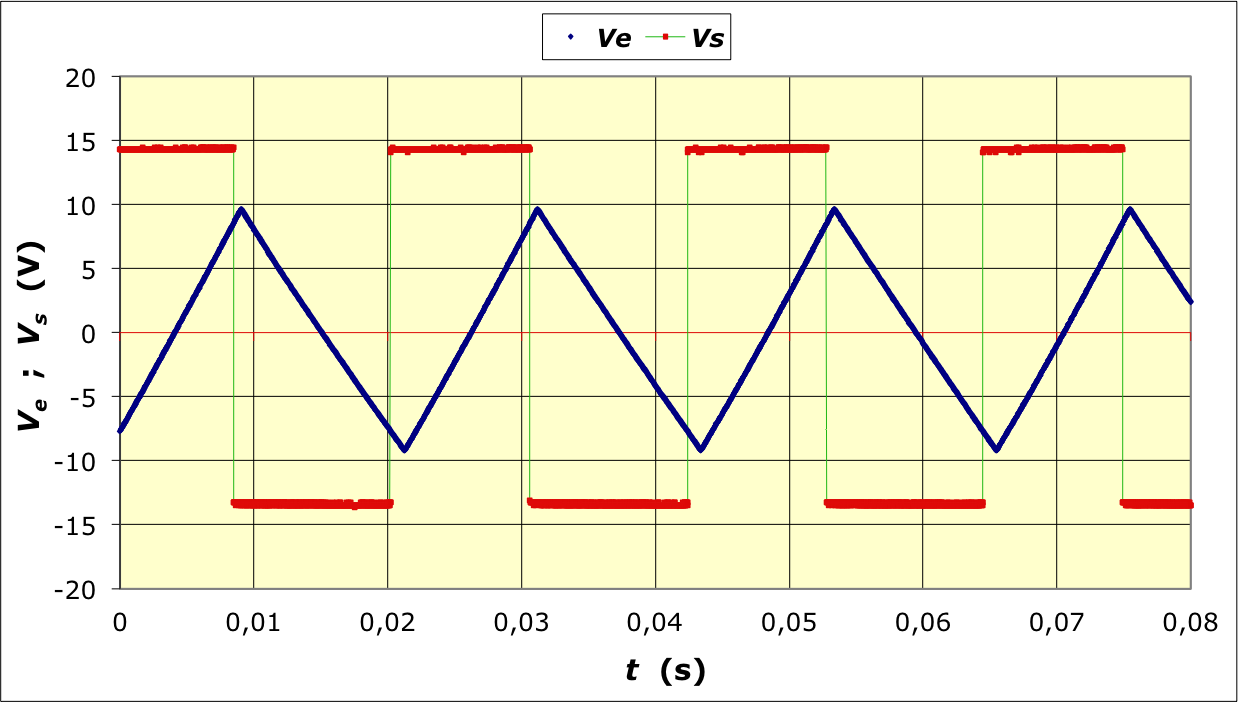
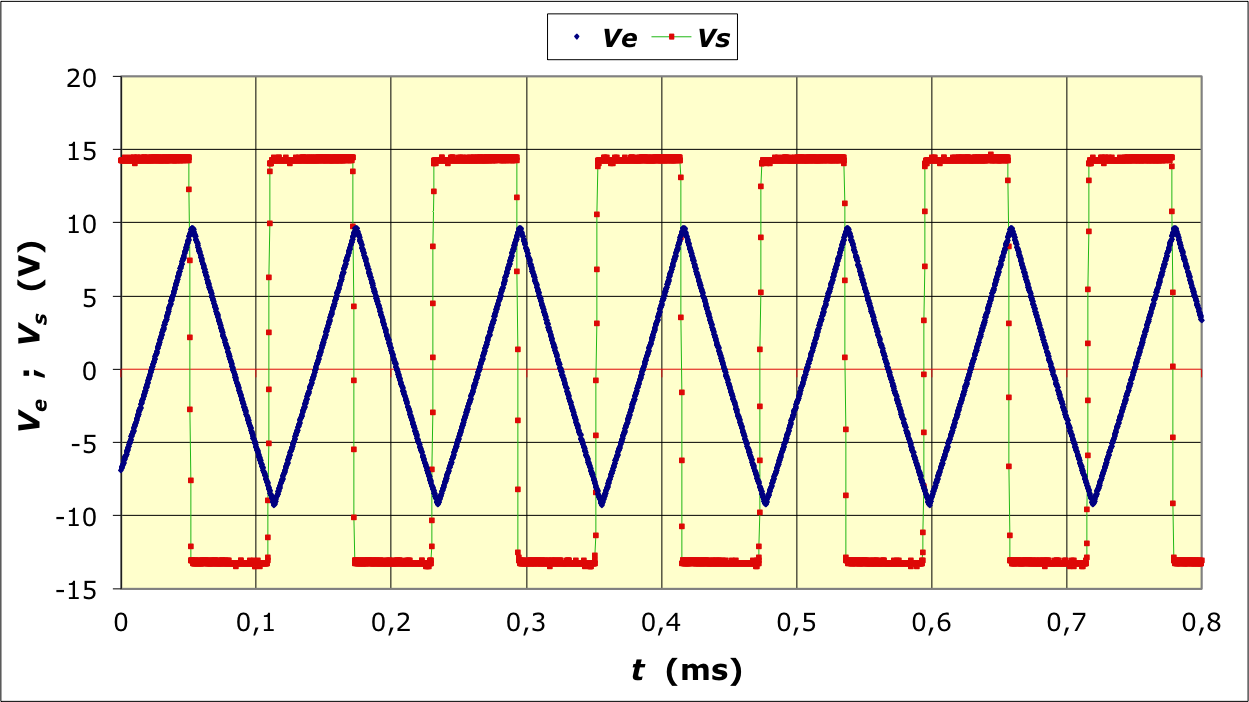
• L’allure des signaux obtenus en mode “A et B” permet aussi d'observer les tensions de “bascule”.

AOidsat_corTP_Im/compar2.png

• Les tensions de “bascule” sont  Vbas+=8,52±0,20VV_{bas+}=\text{8,52}±\text{0,20} \:\mathrm{V}   et   Vbas−=−7,69±0,19VV_{bas-}=-\text{7,69}±\text{0,19} \:\mathrm{V} .  En considérant le gain  G=R1+R2R2=1,70±0,01\displaystyle G=\frac{R_1+R_2}{R_2} =\text{1,70}±{0,01}  ces valeurs sont compatibles avec  Vsat+G=8,4±0,3V\displaystyle \frac{V_{sat+}}{G}=\text{8,4}±\text{0,3} \:\mathrm{V}   et   Vsat−G=−7,9±0,3V\displaystyle \frac{V_{sat-}}{G}=-\text{7,9}±\text{0,3} \:\mathrm{V} .

• Les étudiants de ce groupe de TP se sont alors intéressés à tester l'influence de la vitesse de bascule en effectuant des mesures à une fréquence volontairement exagérée  N=8,24±0,05kHzN=\text{8,24}±\text{0,05} \:\mathrm{kHz}  (mesurée avec le fréquencemètre incorporé). Les signaux enregistrés sur l'ordinateur donnent  N=8,23±0,05HzN=\text{8,23}±\text{0,05} \:\mathrm{Hz}  (après correction de l'échelle de temps).

On réussit alors à obtenir quelques points de mesure sur la durée (en proportion plus longue) de la bascule.

AOidsat_corTP_Im/compar3.png

On constate les saturations pour  Vsat+=14,3±0,5VV_{sat+}=\text{14,3}±\text{0,5} \:\mathrm{V}   et   Vsat−=−13,2±0,5VV_{sat-}=-\text{13,2}±\text{0,5} \:\mathrm{V}  (comparables aux mesures précédentes).

• L’allure des signaux obtenus en mode “A et B” permet aussi d'observer les tensions de “bascule”.

AOidsat_corTP_Im/compar4.png

• Les tensions de “bascule” sont  Vbas+=8,92±0,20VV_{bas+}=\text{8,92}±\text{0,20} \:\mathrm{V}   et   Vbas−=−7,72±0,19VV_{bas-}=-\text{7,72}±\text{0,19} \:\mathrm{V} .  Pour  G=1,70±0,01G=\text{1,70}±\text{0,01}  ces valeurs ne sont pas incompatibles avec  Vsat+G=8,4±0,3V\displaystyle \frac{V_{sat+}}{G}=\text{8,4}±\text{0,3} \:\mathrm{V}   et   Vsat−G=−7,8±0,3V\displaystyle \frac{V_{sat-}}{G}=-\text{7,8}±\text{0,3} \:\mathrm{V} .

• Dans ce cas on peut en outre étudier l'évolution lors de la bascule. Pour décrire la transition entre les deux saturations, on peut considérer l’équation qui décrit l’A.O. réel :  τdVsdt+Vs=με\displaystyle τ \: \frac{dV_s}{dt}+V_s=μ \:ε  en mode linéaire puisqu'alors la sortie n'est pas saturée. On suppose ici une bascule de +A+A à −A-A .

Pour un signal triangulaire, on peut considérer :  Ve=AG+αt\displaystyle V_e=\frac{A}{G}+α \:t  avec  α=4NVemaxα=4 \,N \:V_{emax}  car VeV_e continue à varier pendant la bascule. Avec  ε=VsG−Ve\displaystyle ε=\frac{V_s}{G}- V_e  on obtient :  τdVsdt+Vs.(1−μG)=−μ.(AG+αt)\displaystyle τ \: \frac{dV_s}{dt}+V_s .\left(1-\frac{μ}{G}\right)=-μ .\left(\frac{A}{G}+α \:t\right) .

Mais  μ≫Gμ≫G  donc :  τdVsdt−μGVs≈−μ.(AG+αt)\displaystyle τ \: \frac{dV_s}{dt}-\frac{μ}{G} \:V_s ≈-μ .\left(\frac{A}{G}+α \:t\right) .  Avec  𝒯=Gμτ𝒯=\frac{G}{μ} \: τ  on peut écrire :  𝒯dVsdt−Vs≈−(A+Gαt)\displaystyle 𝒯 \: \frac{dV_s}{dt}-V_s≈-(A+G \:α \:t) .

Les solutions de l'équation “homogène” sont de la forme :  Vs=λet/𝒯V_s=λ \:\mathrm{e}^{t/𝒯}  ;  pour l'équation complète on peut utiliser la méthode de variation de la constante en cherchant :  Vs=λ(t)et/𝒯V_s=λ(t) \:\mathrm{e}^{t/𝒯} .  En reportant dans l'équation, puis en imposant la condition initiale  Vs(0)=AV_s (0)=A  on obtient :  Vs≈A+Gα.(t+𝒯.(1−et/𝒯))V_s≈A+G \:α .\left(t+𝒯.\left(1-\mathrm{e}^{t/𝒯} \right)\right) .

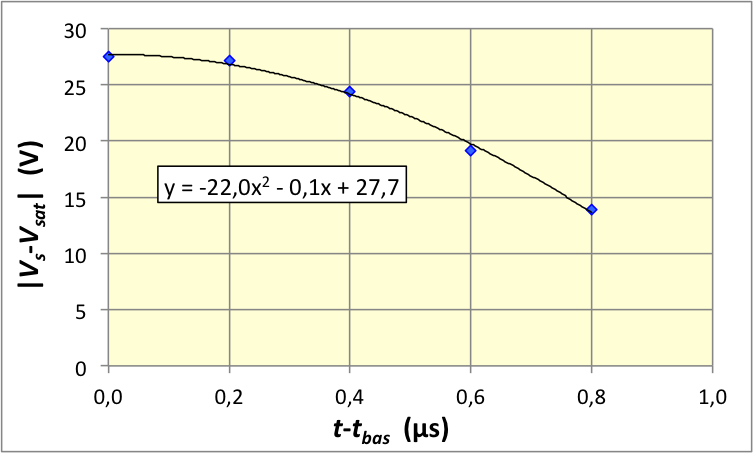
• Pour le début de la bascule, on peut considérer :  et/𝒯≈1+t𝒯+t22𝒯2\mathrm{e}^{t/𝒯}≈1+\frac{t}{𝒯}+\frac{t^2}{2 \,𝒯^2}  ;  Vs≈A−Gαt22𝒯=A−μαt22τ\displaystyle V_s≈A-G \:α \: \frac{t^2}{2 \,𝒯}=A-μ \:α \: \frac{t^2}{2 \,τ} .

En pratique les courbes ajustées sur les données ont un (petit) terme d'ordre 1 car les bascules ne correspondent jamais exactement aux instants de mesure.

AOidsat_corTP_Im/bascule1.png

AOidsat_corTP_Im/bascule2.png

On obtient  μα2τ≈22,8±3,0V.μs−2\displaystyle \frac{μ \:α}{2 \,τ}≈\text{22,8}±\text{3,0} \;\mathrm{V.{μs}^{-2}}  pour les bascules décroissantes et  μα2τ≈10,6±1,5V.μs−2\displaystyle \frac{μ \:α}{2 \,τ}≈\text{10,6}±\text{1,5} \;\mathrm{V.{μs}^{-2}}  pour les bascules croissantes ; cela confirme que la structure interne de l'A.O. n'est pas tout à fait symétrique.

Ceci peut être comparé aux valeurs usuelles  μ≈106μ≈{10}^6  et  τ≈0,1sτ≈\text{0,1} \:\mathrm{s}  avec  α=4NVemax≈0,35V.μs−1α=4 \,N \:V_{emax}≈\text{0,35} \;\mathrm{V.{μs}^{-1}}  ;  on obtient ainsi :  μα2τ≈2V.μs−2\displaystyle \frac{μ \:α}{2 \,τ}≈2 \;\mathrm{V.{μs}^{-2}}  ;  l'A.O. étudié peut être plus rapide  (τ≈0,01sτ≈\text{0,01} \:\mathrm{s}  ;  peu d'exemples de valeurs sont cités) mais on ne dispose pas d'informations suffisantes pour conclure précisément.

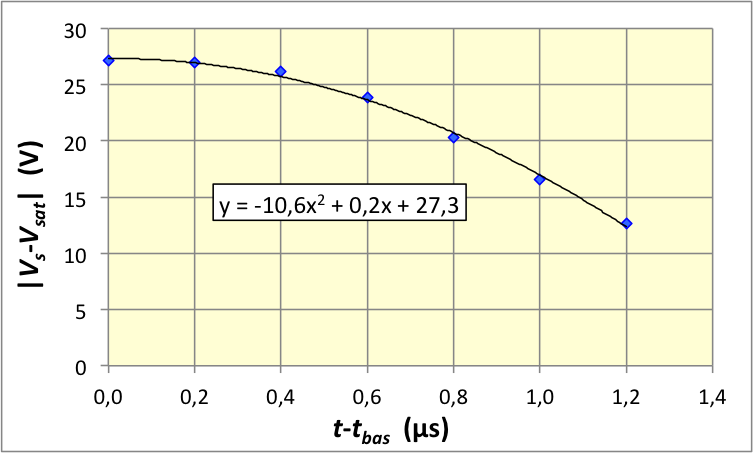
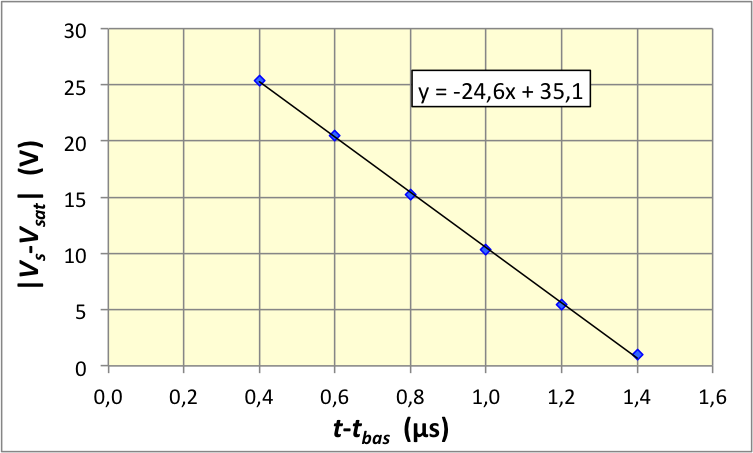
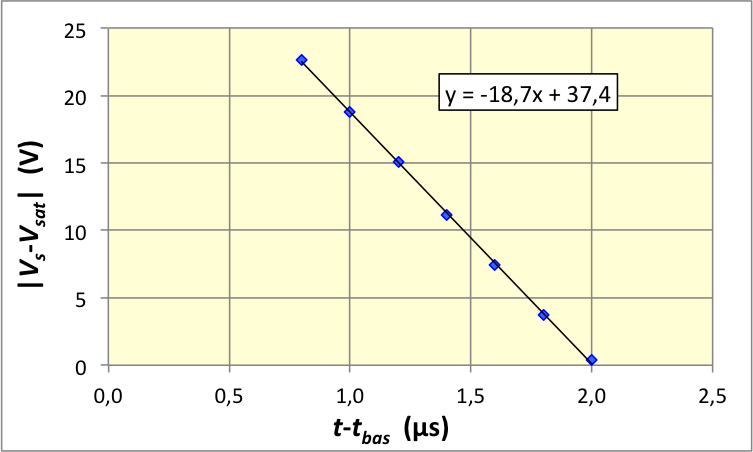
• Pour la suite de la bascule, la “vitesse de balayage”  |dVsdt|\displaystyle \left|\frac{dV_s}{dt}\right|  augmente et arrive à une valeur de saturation ββ .  Tant que la saturation opposée n'est pas atteinte  (Vs≥−VsatV_s≥-V_{sat} ) ceci donne :  Vs≈Cste−β.(t−tbas)V_s≈Cste-β .(t-t_{bas} ) .

AOidsat_corTP_Im/bascule3.png

AOidsat_corTP_Im/bascule4.png

On obtient  β≈24,5±0,3V.μs−1β≈\text{24,5}±\text{0,3} \;\mathrm{V.{μs}^{-1}}  pour les bascules décroissantes et  β≈18,7±0,2V.μs−1β≈\text{18,7}±\text{0,2} \;\mathrm{V.{μs}^{-1}}  pour les bascules croissantes (ici encore dissymétrique). Il existe des A.O. plus rapides, mais aussi des plus lents.

◊ remarque : pour observer plus précisément le balayage non saturé il faudrait αα plus faible, donc un gain GG d'autant plus grand (pour atteindre la limite de bascule), mais il est intéressant d'observer cette saturation.

6. Multivibrateur astable

• En attende de données fournies par les étudiants.

• Pour étudier le modèle théorique, on peut partir du fait qu'on observe expérimentalement une succession de paliers à saturation.

Supposons initialement  Vs=AV_s=A  ;  alors  ε>0ε>0 .  Or  V−<V+=R2R1+R2A\displaystyle V_{-}<V_{+}=\frac{R_2}{R_1+R_2} \: A  impose que le condensateur soit peu chargé ; notons V0V_0 sa tension initiale (on raccordera ensuite quand on repassera par le même état). Ainsi :  V−=V0+∫A−V−RCdt\displaystyle V_{-}=V_0+∫ \frac{A-V_{-}}{R \:C} \: dt ,  ou encore :  RCdV−dt+V−=A\displaystyle R \:C \:\frac{dV_{-}}{dt}+V_{-}=A ,  ce qui donne :  V−=A+(V0−A)e−t/RCV_{-}=A+(V_0-A) \: \mathrm{e}^{-t/RC} .

Ceci aboutit à une bascule pour  A+(V0−A)e−tb/RC=R2R1+R2A\displaystyle A+(V_0-A) \: \mathrm{e}^{-t_b/RC}=\frac{R_2}{R_1+R_2} \: A ,  c'est-à-dire :  (V0−A)e−tb/RC=−R1R1+R2A\displaystyle (V_0-A) \: \mathrm{e}^{-t_b/RC}=-\frac{R_1}{R_1+R_2} \: A .

Le raisonnement est ensuite analogue en partant de  V0′=R2R1+R2A\displaystyle V'_0=\frac{R_2}{R_1+R_2} \: A  ;  le condensateur se décharge puis se recharge en sens inverse jusqu'à une autre bascule et ainsi de suite. Ceci nous conduit à considérer qu'en régime permanent on peut partir de  V0=−R2R1+R2A\displaystyle V_0=-\frac{R_2}{R_1+R_2} \: A ,  donc en reportant :  e−tb/RC=1+2R2R1\displaystyle \mathrm{e}^{-t_b/RC}=1+2 \, \frac{R_2}{R_1}  .

La période correspond à la durée de deux bascules, donc :  T=2RCln(1+2R2R1)T=2 \,RC \: \ln\left(1+2 \,\frac{R_2}{R_1} \right) .

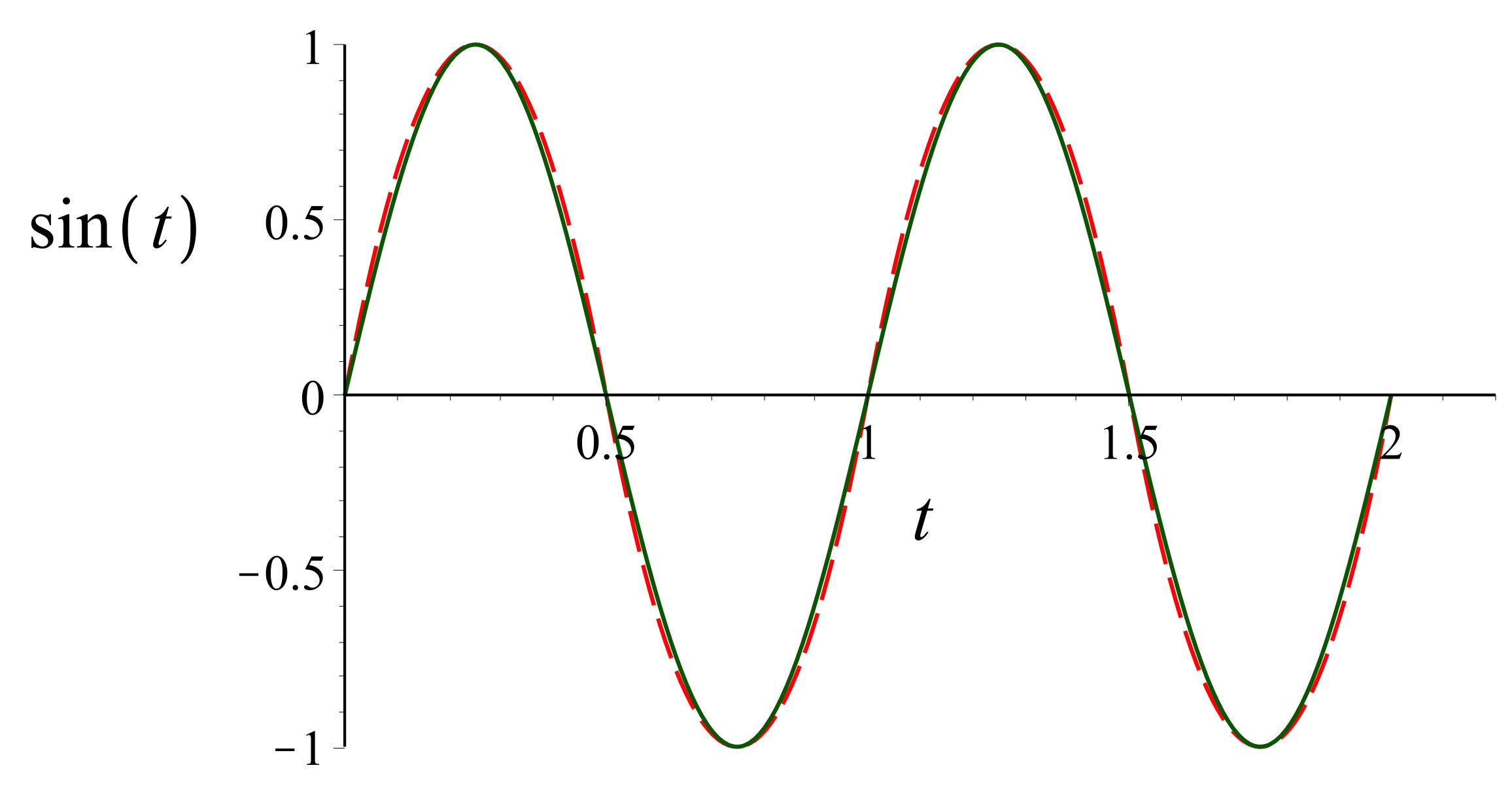
◊ remarque : à partir de cet oscillateur en “créneaux”, il suffit d’ajouter un intégrateur pour obtenir un oscillateur en “dents de scie”, puis d’ajouter un second intégrateur pour obtenir un oscillateur en “arcs de paraboles”... qui ressemble à s’y méprendre à un oscillateur sinusoïdal (approximation suffisante pour de nombreux dispositifs).

AOidsat_corTP_Im/sinus.jpg