AMPLIFICATEUR OPÉRATIONNEL “RÉEL”

AMPLIFICATEUR OPÉRATIONNEL “RÉEL” - TP2

1. Principe

• L'amplificateur opérationnel (A.O.) “idéal” est caractérisé par :

◊	des courants d'entrée, ou “courants de polarisation”, $i_{+}$ et $i_{-}$ nuls (résistances d'entrée infinies) ;
◊	une différence de potentiel entre les deux entrées $ε=v_{+}-v_{-}$ nulle en mode linéaire ;
◊	une tension de sortie $v_s=±A$ (≈ tension d'alimentation) en mode “saturé” ;
◊	une résistance de sortie nulle (générateur de tension parfait).

• L’A.O. “réel” correspond à une description plus complète, qui peut être caractérisée par :

◊

des courants de polarisation très faibles mais non nuls (de l'ordre du nanoampère) ;

◊

une différence de potentiel

ε

telle que, en mode linéaire :

\displaystyle τ \:\frac{dv_s}{dt}+v_s=μ \:ε

avec

μ≈{10}^5

{10}^6

τ≈\text{0,1} \:\mathrm{s}

;

◊

une “vitesse de balayage” en sortie

\displaystyle \frac{dv_s}{dt}=±β

(avec

β≈{10}^6

{10}^7 \: \mathrm{V.s^{-1}}

) en mode “saturé en balayage” ;

◊

une caractéristique de sortie de la forme :

v_s=±(A - ρ \:i_s)

(avec

ρ≈300 \:\mathrm{Ω}

) en mode “saturé” ;

◊

une tension résiduelle de décalage des entrées, non systématiquement compensable, si les gains des deux entrées ne sont pas identiques :

μ_±=μ±δμ

;

\displaystyle τ \: \frac{dv_s}{dt}+v_s=μ_{+} \: v_{+}-μ_{-} \: v_{-}=μ \:ε+v_{ds}

avec

v_{ds}=δμ .(v_{+}+v_{-} )

2. Manipulations

2.1. Tension de décalage des entrées

• En utilisant des signaux oscillant autour d'une moyenne non nulle (sinusoïdal plus décalage continu), tester si la tension de décalage en sortie dépend de la valeur moyenne des signaux en entrée. En déduire éventuellement

δμ

2.2. Gain fini et limitation en fréquence

• Réaliser un montage “amplificateur non inverseur” branché en entrée sur un générateur B.F., avec

R_1≈45 \:\mathrm{kΩ}

R_2≈5 \:\mathrm{kΩ}

(gain

G≈10

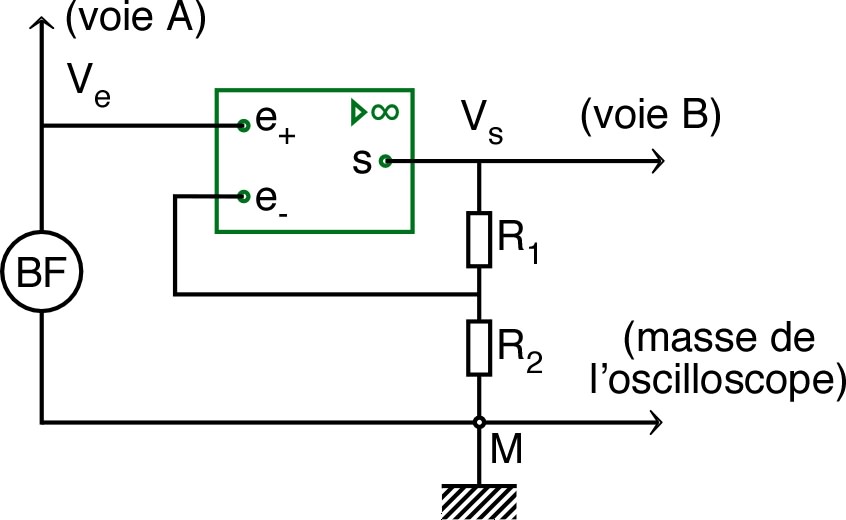
• Relier l'entrée et la sortie du montage aux deux voies d'un oscilloscope, puis, pour une amplitude donnée du générateur (par exemple telle qu’on obtienne

10 \:\mathrm{V}

en sortie), augmenter progressivement la fréquence jusqu'à observer :

\displaystyle H=\frac{V_s}{V_e} ≠\frac{R_1+R_2}{R_1} =G

La manipulation est analogue à celle permettant d'observer la saturation en vitesse de balayage, mais la modification est d'un autre type : avant d'atteindre la saturation en vitesse de balayage, on constate que le gain réel diminue et que

v_s

est déphasée par rapport à

v_e

(en retard), mais non déformée (sinusoïdale, tant qu’on n’atteint pas la limite de balayage en tension

±β

).

• Pour comprendre cet effet, il faut tenir compte du gain

μ

fini de l'A.O. réel : la décroissance du gain correspond à l'effet du terme

\displaystyle \frac{dv_s}{dt}

dans l'équation du régime “linéaire” :

\displaystyle τ \: \frac{dv_s}{dt}+v_s=μ \:ε

. Pour

\underline{ε}=E_m \: \mathrm{e}^{\mathrm{j}ωt}

(petit mais non nul) et

\underline{v}_s=V_{sm} \: \mathrm{e}^{\mathrm{j}(ωt+ϕ)}

(avec des notations complexes), on obtient :

\displaystyle V_{sm} \: \mathrm{e}^{\mathrm{j}ϕ}=\frac{μ}{1+\mathrm{j}ωτ} \: E_m=\underline{μ}' \: E_m

.

Par conséquent, pour

N≈0

on retrouve :

V_{sm}≈μ \:E_m

ϕ≈0

; mais pour

\displaystyle N≫\frac{1}{τ}

on obtient un gain effectif :

\displaystyle μ'=\left|\underline{μ}'\right|=\frac{μ}{\sqrt{1+ω^2 τ^2}} ≈\frac{μ}{ω \:τ}<μ

et un déphasage

ϕ=-\arctan(ω \:τ)≈-\frac{π}{2}

(s'il n'y a pas de saturation en balayage).

• En posant

\displaystyle G=\frac{R_1+R_2}{R_2}

(gain “idéal”), la “fonction de transfert” du montage :

\displaystyle \underline{H}=\frac{\underline{v}_s}{\underline{v}_e}

(avec

\underline{v}_s=V_{sm} \; \mathrm{e}^{\mathrm{j}(ωt+ϕ)}

\underline{v}_e=V_{em} \; \mathrm{e}^{\mathrm{j}ωt}

) donne un gain réel :

\displaystyle H=\left|\underline{H}\right|=\left|\frac{\underline{μ}' \: G}{\underline{μ}'+G}\right|<\min⁡(μ',G)

\displaystyle ϕ=\arg(\underline{H})=-\arctan\left(\frac{G \:ω \:τ}{μ+G}\right)

.

• Cet effet n'apparaît pas pour un montage suiveur de tension, car

G=1≪μ

et les variations de

μ'

sont sans effet sur

\underline{H}

. Par contre pour les montages avec

G

assez grand, ce dernier est limité par le gain

μ

de l'A.O. et les variations de

μ'

imposent des variations analogues pour

\underline{H}

.

• Mesurer alors le gain réel

H

et le déphasage

ϕ

en fonction de la fréquence

N

, puis tracer les courbes représentatives de

\log⁡(H)

ϕ

en fonction de

\log⁡(N)

(“diagrammes de Bode”). Procéder de même pour plusieurs valeurs de

R_1

R_2

correspondant à des gains

G

de l'ordre de

30

100

300

.

• On obtient les représentations logarithmiques suivantes.

• On appelle “fréquence de coupure” la fréquence pour laquelle le gain diminue, par rapport au maximum, d'un facteur

2

en puissance (

\sqrt{2}

en tension, donc aussi en courant dans une résistance de charge). Cela correspond à une coupure à

3 \:\mathrm{dB}

.

• Pour chaque valeur de

G

étudiée, déterminer la fréquence de coupure pour le montage étudié ; en déduire le rapport

\displaystyle \frac{μ}{τ}

AMPLIFICATEUR OPÉRATIONNEL “RÉEL” - TP2

Matériel

Pour chaque groupe (8 groupes)

1 oscilloscope
1 A.O. (à décalage réglable) avec alimentation
1 petit tournevis (si besoin pour décalage)
3 adaptateurs BNC
1 raccord “en T” BNC
1 générateur BF
1 fréquencemètre (sauf si le BF en a un)
1 phasemètre
12 fils (des longs et des courts)
2 câbles coaxiaux (BNC d’un seul côté)
2 câbles coaxiaux (BNC des deux côtés)
2 contrôleurs électroniques
condensateurs divers de

10

100 \:\mathrm{nF}

1 boite de condensateurs

\text{0,1}

1 \:\mathrm{μF}

1 boite de condensateurs

1

10 \:\mathrm{μF}

résistors divers de

100 \:\mathrm{Ω}

1 \:\mathrm{MΩ}

1 boite de résistors

×1

×1000 \:\mathrm{Ω}

1 boite de résistors

×100 \:\mathrm{kΩ}

Au bureau

1 capacimètre
1 A.O. (à décalage réglable) avec alimentation