AMPLIFICATEUR OPÉRATIONNEL “RÉEL”

AMPLIFICATEUR OPÉRATIONNEL “RÉEL” - corrigé des exercices

I. Compensation de l'effet des courants de polarisation

• On peut considérer :

v_{+}=v_e-R_3 \: i_{+}

.
• En notant

\displaystyle i_1=\frac{v_s-v_{-}}{R_1}

\displaystyle i_2=\frac{v_{-}}{R_2} =i_1-i_{-}

(dans les résistances correspondantes) et

\displaystyle H=\frac{R_1+R_2}{R_2}

(gain pour l'A.O. idéal), on obtient :

\displaystyle v_{-}=\frac{1}{H} \: (v_s-R_1 \: i_{-})

.
• En considérant :

v_{+}≈v_{-}

on obtient :

\displaystyle v_e-R_3 \: i_{+}=\frac{1}{H} \: (v_s-R_1 \: i_{-})

puis :

v_s=H \:v_e+R_1 \: i_{-}-H \:R_3 \: i_{+}

2.	• La simplification donne : $\displaystyle v_s=H \:v_e+\left(\frac{R_1 \: R_2}{R_1+R_2}-R_3\right)\:H \:i_{±}$ . • Il est possible de compenser en utilisant $\displaystyle R_3=\frac{R_1 \: R_2}{R_1+R_2}$ ; ceci redonne : $v_s=H \:v_e$ .

• Pour un montage amplificateur inverseur, on peut proposer le schéma analogue ci-contre.
• Avec

\displaystyle i_1=\frac{v_e-v_{-}}{R_1}

\displaystyle i_2=\frac{v_{-}-v_s}{R_2} =i_1-i_{-}

on obtient :

\displaystyle v_{-}=\frac{R_1 \: R_2}{R_1+R_2} \, \left(\frac{v_e}{R_1} +\frac{v_s}{R_2} -i_{-}\right)

• En considérant :

v_{+}=-R_3 \: i_{+}≈v_{-}

on obtient :

\displaystyle -R_3 \: i_{+}=\frac{R_1 \: R_2}{R_1+R_2} \, \left(\frac{v_e}{R_1} +\frac{v_s}{R_2} -i_{-}\right)

• Avec

\displaystyle H=-\frac{R_2}{R_1}

(gain pour l'A.O. idéal), la simplification donne :

\displaystyle v_s=H \:v_e+\left(\frac{R_1 \: R_2}{R_1+R_2}-R_3 \right)\:(1-H) \: i_{±}

.
• Il est possible de compenser en utilisant

\displaystyle R_3=\frac{R_1 \: R_2}{R_1+R_2}

; ceci redonne :

v_s=H \:v_e

II. Mesure du gain différentiel de l'A.O.

1.a.	• On peut écrire : $\displaystyle \frac{v_e-v_s}{r+R}=\frac{ε}{r}=\frac{v_s}{μ \:r}$ .

1.b.	• On peut en déduire : $\displaystyle μ=\frac{v_s}{v_e-v_s} \, \frac{r+R}{r}≈\frac{v_s}{v_e-v_s} \,\frac{R}{r}$ .

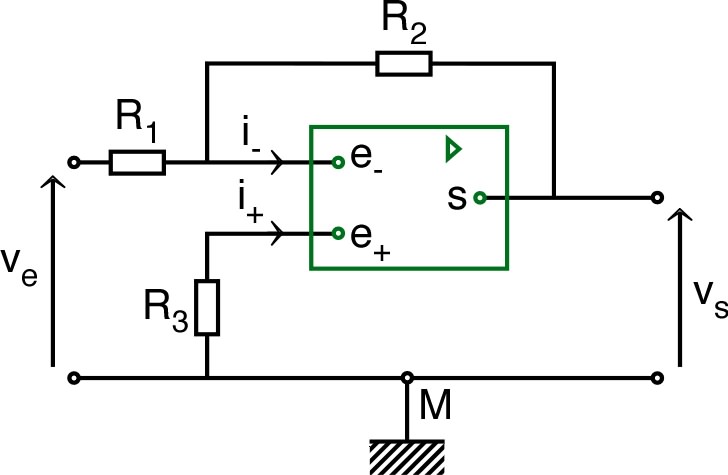
• Le montage amplificateur inverseur de gain

-1

(réalisé avec deux résistances

R'=1 \:\mathrm{kΩ}

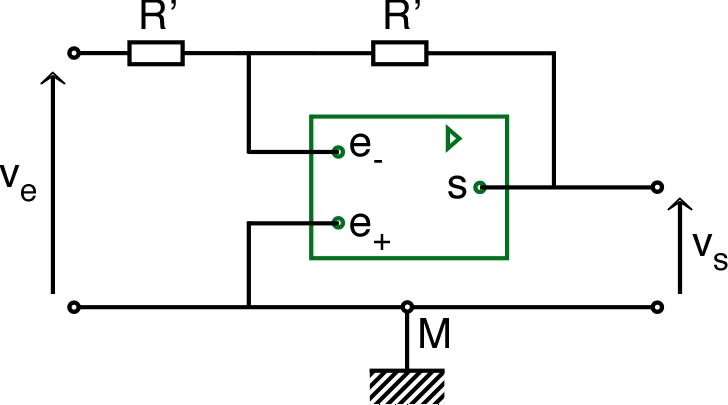
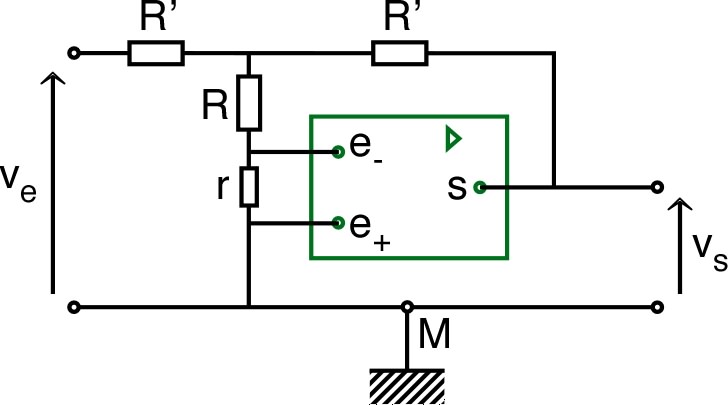
) correspond au premier des schémas suivants ; le montage modifié correspond au second (par analogie, on insère

R

sur la branche de rétroaction et

r

entre les deux entrées).

◊ remarque : en notant

A

le point entre les deux résistances

R'

;

(2 \,G'+G) \:v_A=G' \:v_e+G' \:v_s+G \:v_{-}

(avec les conductances) ;

(g+G) \:v_{-}=G \:v_A

;

v_{+}=0

;

v_s=μ \:ε=-μ \:v_{-}

; la mesure de

v_e

v_s

donne :

\displaystyle μ=-\frac{v_s}{v_e+v_s} \, \frac{(2\, R+R')(R+r)+r \:R'}{r \:R}≈-\frac{v_s}{v_e+v_s} \, \frac{2 \,R+R'}{r}

III. Rôle stabilisateur de la rétroaction

1.a.

• Avec un A.O. idéal, le principe du pont diviseur de tension donne :

\displaystyle v_e=v_{+}=v_{-}=v_s \: \frac{R_2}{R_1+R_2}

.

• Le gain est donc :

\displaystyle H=\frac{v_s}{v_e} =\frac{R_1+R_2}{R_2}

1.b.

• Expérimentalement, si on intervertit les deux entrées

e_{+}

e_{-}

(rétroaction sur

e_{+}

) on constate le montage devient inopérant en tant qu'amplificateur non inverseur car il se comporte en comparateur inverseur (régime saturé).
• Cela se déduit pas des équations précédentes car le changement de signe de

ε≈0

y est sans effet. Intuitivement, on peut deviner que le régime devient instable : la moindre perturbation est amplifiée puis réinjectée en entrée avec le même signe... et ainsi de suite, d'où une inévitable divergence.

2.a.	• Le montage correspond à : $\displaystyle ε=v_e-\frac{R_2}{R_1+R_2} \: v_s$ d'où on déduit : $\displaystyle τ \: \frac{dv_s}{dt}+\left(1+\frac{μ}{H}\right) \: v_s=μ \:v_e$ . • Pour $v_e (t)$ constant par morceaux, les solutions sont de la forme : $\displaystyle v_s=\frac{H \:μ}{H+μ} \: v_e+U\;\mathrm{e}^{-t/T}$ avec $\displaystyle T=\frac{H}{H+μ} \: τ$ et où $U$ est une constante d'intégration à déterminer. • Pour $t<0$ la seule solution raisonnable est $v_s (t)=0$ . • Pour $t>0$ la continuité du signal de sortie (dans l'équation, la dérivée $\displaystyle \frac{dv_s}{dt}$ ne peut pas être infinie) impose : $\displaystyle 0=\frac{H \:μ}{H+μ} \: E+U$ d'où $\displaystyle v_s=\frac{H \:μ}{H+μ} \: E .\left(1-\mathrm{e}^{-t/T} \right)$ . • La tension $v_s (t)$ tend donc exponentiellement vers $\displaystyle \frac{H \:μ}{H+μ} \: E≈H \:E$ , valeur proche de celle correspondant à l'A.O. idéal mais tenant compte du gain fini ( $μ≫H$ ).

2.b.	• L'interversion des deux entrées $e_{+}$ et $e_{-}$ (rétroaction sur $e_{+}$ ) correspond à : $\displaystyle ε=\frac{R_2}{R_1+R_2} \: v_s-v_e$ d'où on déduit : $\displaystyle τ \: \frac{dv_s}{dt}+\left(1-\frac{μ}{H}\right) \: v_s=-μ \:v_e$ . • Pour $v_e (t)$ constant par morceaux, les solutions sont de la forme : $\displaystyle v_s=\frac{μ \:H}{μ-H} \: v_e+U \;\mathrm{e}^{t/T}$ avec $\displaystyle T=\frac{H}{μ-H} \: τ$ et où $U$ est une constante d'intégration à déterminer. • Pour $t<0$ la seule solution raisonnable est $v_s (t)=0$ . • Pour $t>0$ la continuité du signal de sortie impose : $\displaystyle 0=\frac{μ \:H}{μ-H} \: E+U$ d'où $\displaystyle v_s=\frac{μ \:H}{μ-H} \: E .\left(1-\mathrm{e}^{t/T} \right)$ . • La tension $v_s (t)$ diverge donc exponentiellement en s'éloignant de $\displaystyle \frac{μ \:H}{μ-H} \: E≈H \:E$ , valeur proche de celle correspondant à l'A.O. idéal mais tenant compte du gain fini ( $μ≫H$ ). • Cette divergence aboutit à la saturation, avec un signe contraire à $E$ (celui du terme exponentiel), d'où un comportement de comparateur inverseur.

IV. Gain en mode commun

• La relation

v_s=μ_{+} \: v_{+}-μ_{-} \: v_{-}

peut s'écrire avec

\displaystyle μ=\frac{μ_{+}+μ_{-}}{2}

(gain moyen) et

μ_{mc}=μ_{+}-μ_{-}

; ainsi :

\displaystyle v_s=μ .(v_{+}-v_{-} )+μ_{mc} \: \frac{v_{+}+v_{-}}{2}

où le second terme décrit l'effet du potentiel moyen. On souhaite que l'A.O. soit un “amplificateur différentiel”, seulement sensible à

v_{+}-v_{-}

et sans le second terme.