AMPLIFICATEUR OPÉRATIONNEL “RÉEL” - exercices


I. Compensation de l'effet des courants de polarisation

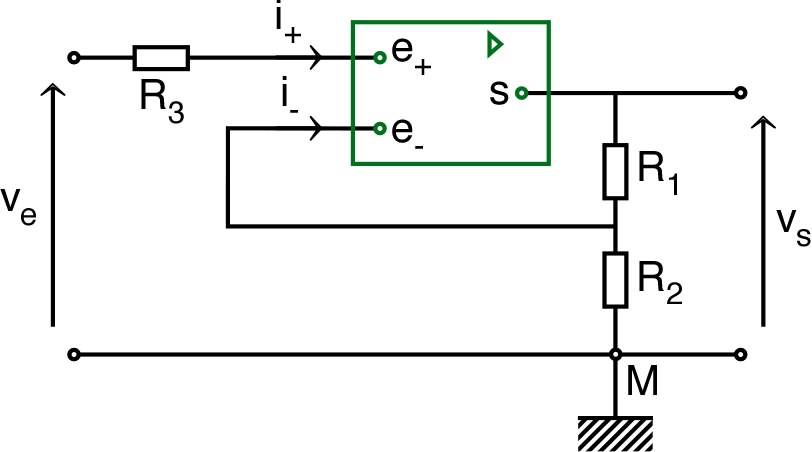
        • On considère un montage amplificateur non inverseur réalisé à l'aide d'un A.O. réel. Les courants de polarisation sont le seul défaut pris en compte ici. Une résistance R3R_3 a été ajoutée pour compenser leur effet.

1.     • Exprimer vsv_s en fonction de vev_e , R1R_1 , R2R_2 , R3R_3 , i+i_{+} et i−i_{-} .

2.     • On suppose  i+≈i−i_{+}≈i_{-}  ;  montrer qu'on peut compenser l'effet des courants de polarisation en choisissant une valeur appropriée de R3R_3 .
AOreel_ex_Im/AOreel_ex_Im1.jpg

3.     • Montrer qu'il est possible de procéder de façon analogue pour un montage amplificateur inverseur.


II. Mesure du gain différentiel de l'A.O.

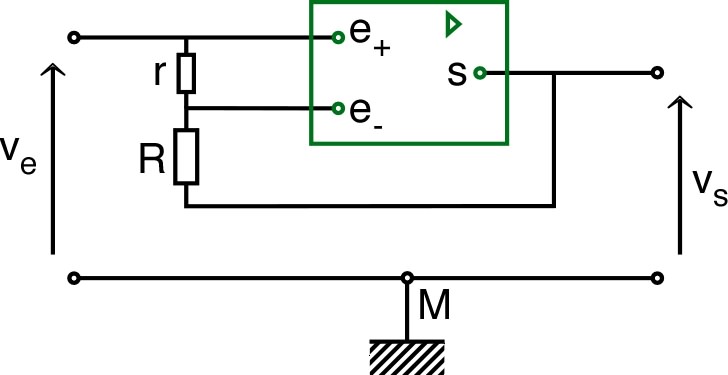
        • On considère un montage suiveur réalisé à l'aide d'un A.O. réel. Le gain différentiel fini μμ est le seul défaut pris en compte ici. Deux résistances  r=100Ωr=100 \:\mathrm{Ω}  et  R=100kΩR=100 \:\mathrm{kΩ}  ont été ajoutées pour mesurer μμ .

1.     a) Exprimer la relation entre le gain μμ de l'A.O., les potentiels vev_e et vsv_s et les résistances rr et RR .
        b) Montrer qu'on peut calculer μμ d'après les mesures de vev_e et vsv_s .
AOreel_ex_Im/AOreel_ex_Im2.jpg

2.     • Sans effectuer les calculs, indiquer le schéma analogue, basé sur un montage amplificateur inverseur de gain −1-1 (réalisé avec deux résistances  R′=1kΩR'=1 \:\mathrm{kΩ} )  auquel on ajoute les deux résistances rr et RR .


III. Rôle stabilisateur de la rétroaction

1.     a) Rappeler le calcul du gain d'un montage amplificateur non inverseur construit avec un A.O. idéal.
        b) Comment se comporte le montage si on intervertit les deux entrées e+e_{+} et e−e_{-} (rétroaction sur e+e_{+}) ?

2.     • On tient compte maintenant du fonctionnement d'un A.O. réel :  τdvsdt+vs=με\displaystyle τ \: \frac{dv_s}{dt}+v_s=μ \:ε  (mais on ne tient pas compte des autres défauts). On impose alors au montage amplificateur non inverseur une tension en échelon :  ve(t)=0v_e (t)=0  pour  t<0t<0  ;  ve(t)=Ev_e (t)=E  pour  t>0t>0 .
        a) Montrer que la tension vs(t)v_s (t) tend exponentiellement vers une valeur proche de celle correspondant à l'A.O. idéal (mais tenant compte du gain fini μμ).
        b) Montrer que l'interversion des deux entrées e+e_{+} et e−e_{-} (rétroaction sur e+e_{+}) conduit au contraire à une divergence exponentielle : la tension de sortie s'éloigne de la limite obtenue à la question précédente et tend vers la saturation, d'où un comportement de comparateur inverseur.


IV. Gain en mode commun

        • Les deux entrées d'un A.O. réel ne sont pas rigoureusement symétriques :  vs=μ+v+−μ−v−v_s=μ_{+} \: v_{+}-μ_{-} \: v_{-}  (mais c'est le seul défaut pris en compte ici).
        • Montrer qu'on peut exprimer cet effet en ajoutant à l'équation classique (avec un gain μμ) un terme avec un “gain en mode commun” μmcμ_{mc} (généralement imposé très faible par construction :  μmc≈10−5μμ_{mc}≈{10}^{-5} \: μ).