AMPLIFICATEUR OPÉRATIONNEL IDÉAL ; RÉGIME LINÉAIRE - exercices


A. EXERCICES DE BASE

I. Capacité réglable

        • On considère le montage suivant réalisé à l'aide de deux A.O. parfaits fonctionnant en régime linéaire.

AOidlin_ex_Im/AOidlin_ex_Im1.jpg

        • L'ensemble, inséré dans un circuit par l'intermédiaire des deux bornes AA et BB ,  se comporte comme un dipôle soumis à une tension vev_e et parcouru par un courant ii .

1.     a) Exprimer la relation entre le courant ii et la charge qq de la plaque de gauche du condensateur.
        b) Exprimer vs1v_{s1} en fonction de vev_e ; préciser à quoi sert le premier A.O..

2.     a) Quel est le potentiel du point EE ?
        b) En déduire le courant i1i_1 (fourni par la sortie du premier A.O.) traversant la résistance R1R_1 .

3.     a) En déduire vs2v_{s2} en fonction de vev_e et des résistances.
        b) En déduire la relation entre la charge qq accumulée et la tension vev_e imposée au montage.
        c) Justifier que le montage se comporte comme un condensateur de capacité  C=C0R1+R2R1\displaystyle C=C_0 \:\frac{R_1+R_2}{R_1} .


II. Filtre actif “passe-bande”

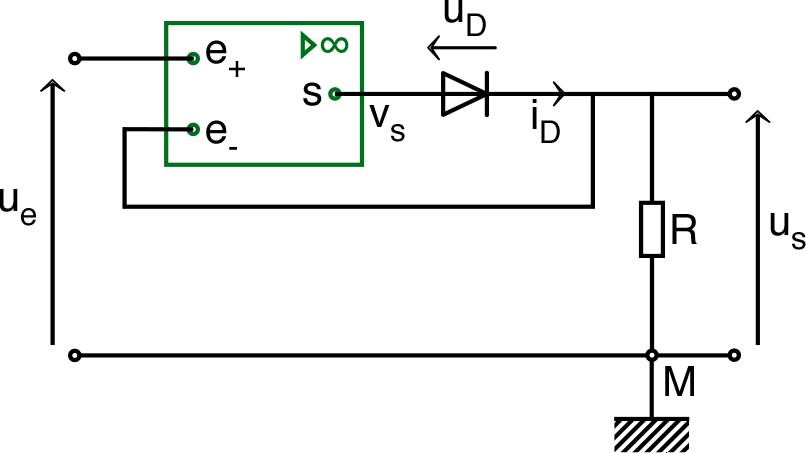
        • On considère le montage ci-contre (de type “filtre de Rauch”), réalisé à l'aide d'un A.O. parfait fonctionnant en régime linéaire. La tension vev_e imposée en entrée est sinusoïdale de pulsation ωω .

1.     a) En utilisant les notations complexes, exprimer v_A\underline{v}_A en fonction de v_e\underline{v}_e ,  v_e−\underline{v}_{e_{-}} ,  v_s\underline{v}_s ,  RR  et  CC .
        b) En déduire v_s\underline{v}_s en fonction de v_e\underline{v}_e ,  RR , CC  et  C0C_0 .		 AOidlin_ex_Im/AOidlin_ex_Im2.jpg

2.     a) Déterminer la pulsation ω0ω_0 telle que le gain  H=|v_sv_e|\displaystyle H=\left|\frac{\underline{v}_s}{\underline{v}_e} \right|  soit maximal.
        b) Calculer le gain maximum  H0=H(ω0)H_0=H(ω_0) .

3.     • On définit la bande passante par ses limites ω1ω_1 et ω2ω_2 telles que  H(ω1)=H(ω2)=H02\displaystyle H(ω_1)=H(ω_2)=\frac{H_0}{\sqrt{2}} .
        a) Déterminer la largeur de bande passante  ∆ω=ω2−ω1∆ω=ω_2-ω_1 .
        b) En déduire la largeur relative de bande passante  ∆ωω0\displaystyle \frac{∆ω}{ω_0} .


B. EXERCICE D'APPROFONDISSEMENT

III. Redresseur “idéal”

        • On considère le montage suivant réalisé à l'aide d'un A.O. parfait, d'une résistance  R=10kΩR=10 \:\mathrm{kΩ}  et d'une diode dont la caractéristique peut s'écrire :  iD=I0.(eλuD−1)i_D = I_0 .\left(\mathrm{e}^{λ \,u_D}-1\right)  avec  I0=5nAI_0=5 \:\mathrm{nA}  et  λ=20V−1λ=20 \:\mathrm{V^{-1}} .

AOidlin_ex_Im/AOidlin_ex_Im3.jpg

1.     • On suppose que l'A.O. fonctionne en régime linéaire (non saturé en tension).
        a) Exprimer usu_s en fonction de ueu_e .
        b) En supposant que la sortie du montage ne débite pas de courant, en déduire le courant iDi_D débité à travers la diode par la sortie de l'A.O..
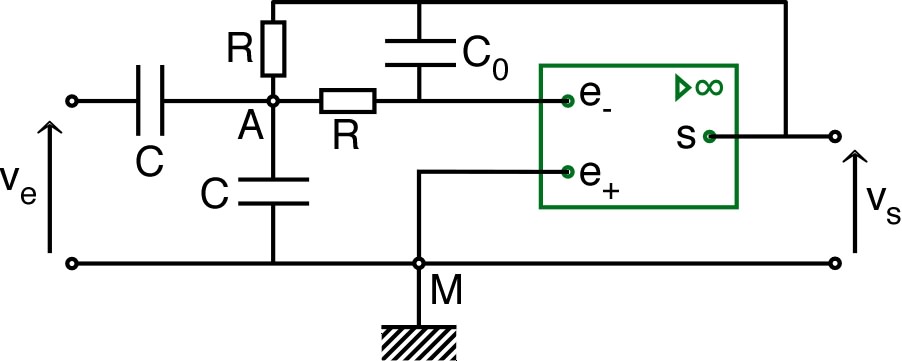        c) En déduire la tension uDu_D aux bornes de la diode, en fonction de  λλ ,  ueu_e ,  RR  et  I0I_0 .
        d) Exprimer le potentiel vsv_s de sortie de l'A.O. en fonction de ueu_e et uDu_D ,  puis en fonction de  λλ ,  ueu_e ,  RR  et  I0I_0 .


2.     a) Quelle est la tension ueu_e maximum au delà de laquelle la sortie de l'A.O. est saturée ?
        b) Quelle est la tension ueu_e minimum en deçà de laquelle la sortie de l'A.O. est saturée ?

3.     • Lorsque la tension de sortie est saturée, la propriété  ε=v+−v−≈0ε=v_{+}-v_{-}≈0  n'est plus vérifiée et cette quantité prend une valeur imposée par le reste du montage. On considère ici la saturation pour  vs<0v_s<0 .
        a) Quel est dans ce cas l'ordre de grandeur du courant iDi_D dans la diode ?
        b) Quelle est alors la tension usu_s ? Justifier que le montage soit nommé “redresseur”.
        c) Que vaut la tension uDu_D dans ces conditions ?
        d) Que vaut alors  ε=v+−v−ε=v_{+}-v_{-} ?
        e) Le rôle de la saturation est il nuisible ou utile dans ce montage ?