TRACÉ ET MODÉLISATION DE CARACTÉRISTIQUES

TRACÉ ET MODÉLISATION DE CARACTÉRISTIQUES - TP4

1. Résistance d’un générateur

• Les sciences expérimentales (entre autres) nécessitent souvent de l’imagination ; toutes les procédures expérimentales imaginables sont bonnes pourvu qu’elles aboutissent à mesurer correctement ce qu’on recherche, avec une précision satisfaisante.

• Dans ce montage, on utilise comme générateur réglable la sortie “continu” du générateur B.F. : on connaît sa résistance interne

R_0=50,0±0,5 \:\mathrm{Ω}

.

• On se propose de vérifier à l’ohmmètre la valeur de cette résistance en “arrêtant” le générateur (c’est-à-dire qu’on le laisse en marche mais qu’on règle une force électromotrice nulle en sortie).

La difficulté est qu’il est pratiquement impossible d’annuler rigoureusement la force électromotrice (f.e.m.), et que l’ohmmètre y est très sensible (il doit faire circuler du courant pour effectuer la mesure, or le courant est perturbé par la moindre f.e.m. du générateur).

• Pour différentes valeurs faibles de la f.e.m.

E≈0

(mesurée avec un voltmètre), mesurer la résistance apparente

r_{app}

indiquée par l’ohmmètre. Tracer la courbe représentant

r_{app}

en fonction de

E

; la résistance

r

du générateur correspond à l’intersection avec l’axe des ordonnées (pour

E=0

) :

r=r_{app} (0)

.

◊ remarque : pour cette manipulation, il est important de bien choisir le calibre le mieux adapté de l’ohmmètre puis de ne plus en changer pour l’ensemble des mesures correspondantes (sinon, cela change la résistance en série avec celle du générateur, donc on ne peut plus séparer l’effet de

r

et l’effet de la f.e.m. parasite).

2. Représentations de Thévenin et de Norton

• Régler une valeur de

1

5 \:\mathrm{V}

pour la f.e.m.

E_0

du générateur (égale à la tension “à vide” mesurée avec un voltmètre de grande résistance) ; ce réglage doit ensuite rester inchangé pendant toute l’expérience.

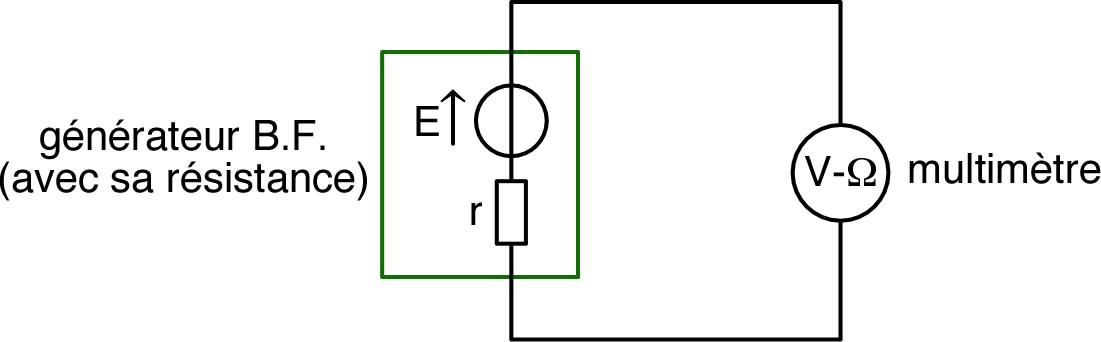
• Après avoir mesuré, à l'aide d'un ohm-mètre électronique, la résistance de chacun des résistors utilisés, réaliser le circuit ci-contre.

◊ remarque : utiliser des résistances différentes, mais du même ordre de grandeur (entre

50

1000 \:\mathrm{Ω}

).

• Mesurer quelques points de fonctionnement du générateur équivalent entre

A

B

, c’est-à-dire mesurer

U_{AB}

I

en sortie pour différentes valeurs de

R'

. Vérifier que la caractéristique est affine :

U_{AB}=E-R \:I

, puis en déduire les valeurs expérimentales de

E

R

I_c

équivalents.

• Comparer les valeurs

E

R

I_c

équivalentes aux résultats des calculs “théoriques” :

E=E_0 \:\frac{R_2 \:R_3-R_1 \:R_4}{(R_1+R_3 )(R_2+R_4 )+R_0 .(R_1+R_2+R_3+R_4 )}

;

I_c=E_0 \frac{R_2 \:R_3-R_1 \:R_4}{R_0 .(R_1+R_3 )(R_2+R_4 )+R_1 \:R_2 .(R_3+R_4 )+R_3 \:R_4 .(R_1+R_2 )}

;

R=\frac{E}{I_c}

◊ remarque : cette propriété se généralise : toute association en réseau de dipôles linéaires donne pour l'ensemble un comportement linéaire (ceci constitue le(s) théorème(s) de Thévenin/Norton).

3. Pont de Wheatstone et mesure d’une résistance

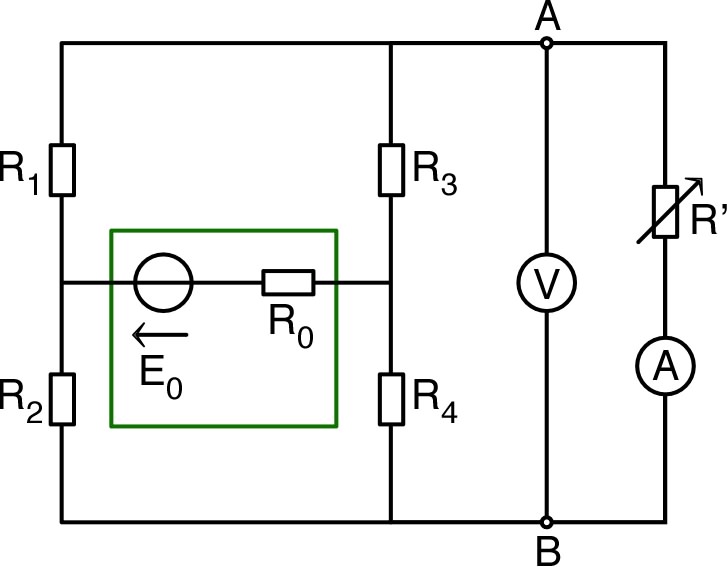
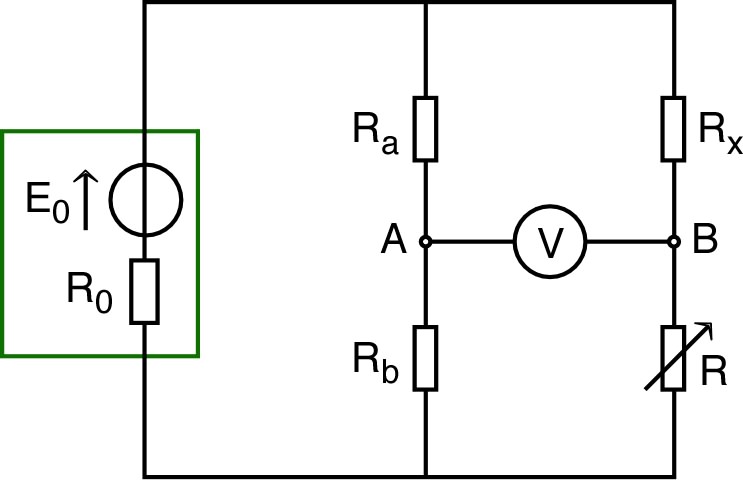
• Réaliser le circuit ci-contre (pont de Wheatstone), avec deux résistances

R_a

R_b

(connues précisément), une boite de résistance étalonnée réglable

R

et une résistance inconnue

R_x

.

◊ remarque : il existe des ponts de Wheatstone “préfabriqués”.

• Pour

E_0

fixé (générateur annexe), ajuster les ordres de grandeur de

R_a

R_b

de telle façon à annuler approximativement la tension

U_{AB}

(ne pas oublier de remesurer précisément

R_a

R_b

après le choix final). Ajuster plus précisément

R

pour annuler

U_{AB}

le mieux possible.

D'après le principe du pont diviseur de tension, ceci correspond à la condition :

\frac{R_x}{R}=\frac{R_a}{R_b}

d’où on déduit la résistance à mesurer :

R_x=R \:\frac{R_a}{R_b}

.

◊ remarque : en pratique, l'ajustement de

R

peut manquer de précision (si le réglage optimal est intermédiaire entre deux graduations) ; dans ce cas, mesurer

U_{AB} (R)

pour les valeurs de

R

telles que

U_{AB}≈0

, tracer la courbe correspondante, puis déterminer graphiquement la condition d’équilibre correspondant à la valeur particulière

R=R_e

telle que

U_{AB} (R_e )=0

.

◊ remarque : en pratique, puisque

U_{AB}=0

à l'équilibre, il ne circule aucun courant si on remplace le voltmètre par un ampèremètre ; le voltmètre est nécessaire au début (avant “d’équilibrer” le pont, le courant peut être grand et risque de dépasser la limite supportée par l’ampèremètre), mais l’ampèremètre (microampèremètre) peut être plus précis à la fin (au voisinage de l’équilibre).

◊ remarque : on peut vérifier que ce montage est analogue au montage précédent (seule la disposition des fils est représentée différemment) ; les relations précédentes correspondent à

E=0

I_c=0

(avec les notations correspondantes), c'est-à-dire :

R \:R_a=R_x\: R_b

TRACÉ ET MODÉLISATION DE CARACTÉRISTIQUES - TP4

Matériel (10 groupes)

Pour chaque groupe

3 adaptateurs BNC
1 générateur BF
1 générateur

6 \:\mathrm{V}

2 \:\mathrm{A}

(continu et alternatif)
12 fils (des longs et des courts)
2 câbles coaxiaux (BNC d’un seul côté)
2 câbles coaxiaux (BNC des deux côtés)
2 contrôleurs électroniques
1 boite de résistors

×1

×1000 \:\mathrm{Ω}

1 rhéostat

≈1000 \:\mathrm{Ω}

Au bureau

divers résistors

≈100 \:\mathrm{Ω}

100 \:\mathrm{kΩ}