TRACÉ ET MODÉLISATION DE CARACTÉRISTIQUES

TRACÉ ET MODÉLISATION DE CARACTÉRISTIQUES - corrigé du TP4

1. Résistance d’un générateur

• Pour mesurer une résistance, l'ohm-mètre utilise son alimentation pour imposer un courant dans le dipôle étudié et compare (puisque c'est un voltmètre) la tension correspondante à celle aux bornes d'une résistance étalon parcourue par le même courant :

Thevenin_corTP4_im/Thevenin_corTP4-im1.jpg

• L'ensemble étant parcouru par un même courant, le principe du pont diviseur de tension permet d'en déduire la résistance :

r=r' \frac{U}{U'}

.

• Si au contraire on branche un générateur dont la force électromotrice n'est pas nulle, les tensions mesurées ne correspondent pas à ce qui est supposé par le procédé de mesure :

Thevenin_corTP4_im/Thevenin_corTP4-im2.jpg

Le courant est dans ce cas :

I=\frac{E'-E}{r'+r}

donc les tensions mesurées sont (avec le générateur considéré comme récepteur) :

U= E+r \:I=\frac{r \:E'+r' \:E}{r'+r}

U'=r' \:I=r' \,\frac{E'-E}{r'+r}

.

L'ohm-mètre affiche alors la grandeur :

r_{app}=r' \frac{U}{U'}=\frac{r \:E'+r \:E}{E'-E}

qui n'est pas une expression affine de

E

. Toutefois, pour

E≪E'

, on peut considérer :

r_{app}=r \frac{1+\frac{r'}{r} \frac{E}{E'}}{1-\frac{E}{E'}}≈r .\left(1+\frac{r'+r}{r \:E'} E\right)=r+\frac{r'+r}{E'} E

.

◊ remarque : ce raisonnement n'est pas indispensable, puisqu'au voisinage de

E=0

toute courbe relativement régulière peut être approchée par sa tangente à l'origine : il suffit de considérer la limite correspondant à l'intersection de la courbe avec l'axe ; néanmoins, il est toujours nécessaire de comprendre les méthodes de mesure afin d'en connaitre les limites.

• Un premier groupe obtient des résultats plutôt satisfaisants, correspondant à

r=51,6±0,2 \:\mathrm{Ω}

; bien que l'écart soit le triple de l'incertitude (malgré une approche de

E=0

à l'échelle du

\mathrm{µV}

) cela n'est pas incompatible avec l'indication du fabriquant

50,0±0,5 \:\mathrm{Ω}

Un autre groupe obient des résultats analogues, mais montrant clairement que les étudiants ont changé de calibre pour les mesures extrêmes (qui doivent donc être mises à part). Ils en déduisent

r=53,7±0,4 \:\mathrm{Ω}

; bien que du bon ordre de grandeur, cela ne semble pas compatible avec l'indication du fabriquant (certaines causes d'incertitudes expérimentales ont probablement été sous-estimées). Il est vrai en fait que l'approche de

E=0

n'a été réalisée qu'à l'ordre du

\mathrm{mV}

, avec peu de mesures au voisinage immédiat de

E=0

, ce qui n'est probablement pas assez précis (pente

4,6 \:\mathrm{Ω.mV^{-1}}

). Cela est probablement dû à un mauvais choix du calibre utilisé sur le générateur : calibre

10 \:\mathrm{V}

au lieu du petit calibre

1 \:\mathrm{V}

(et de ce fait aussi sur l'ohm-mètre).

2. Représentations de Thévenin et de Norton

• La f.e.m.

E

correspond à la tension

U_{AB}

dans le cas particulier où le courant en sortie

I

est nul.

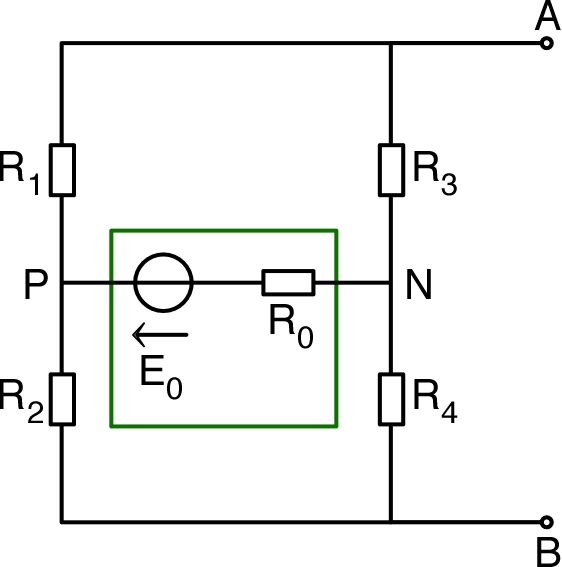
Dans ces conditions, le courant est le même dans

R_1

R_3

(ainsi en série) donc le principe du pont diviseur de tension permet de calculer :

U_{AN}=\frac{R_3}{R_1+R_3} U_{PN}

et de même

U_{BN}=\frac{R_4}{R_2+R_4} U_{PN}

.

Ainsi :

E=U_{AB}=U_{AN}-U_{BN}=\frac{R_2 \,R_3-R_1 \,R_4}{(R_1+R_3)(R_2+R_4)} \:U_{PN}

.

• Or, le générateur est alors branché sur une résistance équivalente à

R_1+R_3

en parallèle avec

R_2+R_4

R'=\frac{(R_1+R_3 )(R_2+R_4 )}{R_1+R_2+R_3+R_4}

.

Le principe du pont diviseur de tension indique donc :

U_{PN}=\frac{R'}{R_0+R'} \:E_0

Thevenin_corTP4_im/Thevenin_corTP4-im3.jpg

• La combinaison de ces relations donne finalement :

E=E_0 \frac{R_2 \:R_3-R_1 \:R_4}{(R_1+R_3 )(R_2+R_4 )+R_0.(R_1+R_2+R_3+R_4 )}

.

• Inversement, le courant de court-circuit

I_c

correspond au courant de sortie

I

dans le cas particulier où la tension

U_{AB}

est nulle (court-circuit).

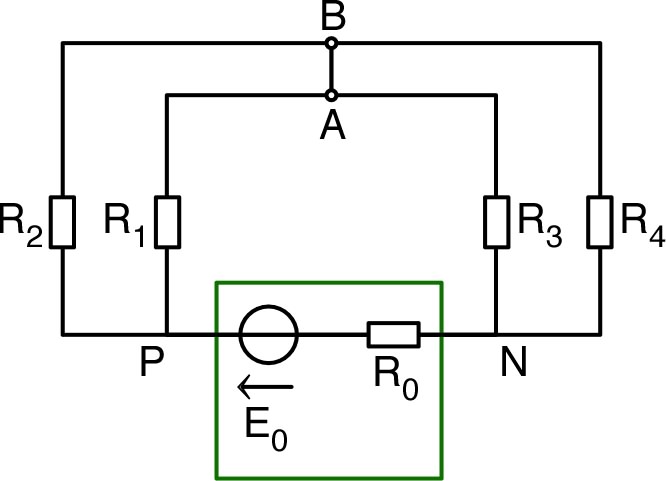
Dans ces conditions, la tension est la même pour

R_1

R_2

(ainsi en parallèle) donc le principe du pont diviseur de courant donne :

I_1=\frac{G_1}{G_1+G_2} \:I_0=\frac{R_2}{R_1+R_2} \:I_0

et de même

I_3=\frac{R_4}{R_3+R_4} \:I_0

.

Ainsi :

I_c=I_{AB}=I_1-I_3=\frac{R_2 \,R_3-R_1 \,R_4}{(R_1+R_2 )(R_3+R_4 )} \:I_0

.

• Par ailleurs, le générateur est alors branché sur une résistance équivalente à l'assemblage en série de

\frac{R_1 \:R_2}{R_1+R_2}

(

R_1

R_2

en parallèle) et de

\frac{R_3 \:R_4}{R_3+R_4}

; ainsi :

R''=\frac{R_1 \:R_2}{R_1+R_2}+\frac{R_3 \:R_4}{R_3+R_4}

.

La loi de Pouillet indique alors :

I_0=\frac{E_0}{R_0+R''}

Thevenin_corTP4_im/Thevenin_corTP4-im4.jpg

• La combinaison de ces relations donne finalement :

I_c=E_0 \frac{R_2 \:R_3-R_1 \:R_4}{R_0.(R_1+R_2 )(R_3+R_4 )+R_1 \,R_2.(R_3+R_4 )+R_3 \,R_4.(R_1+R_2 )}

.

• Pour la confrontation à l'expérience : en attente de données fournies par les étudiants...

3. Pont de Wheatstone et mesure d’une résistance

• La condition

R_x=R \:\frac{R_a}{R_b}

permet de calculer la résistance étudiée ; toutefois, cela cumule les incertitudes sur les résistances, de l'ordre de

0,5 \:%

en valeur relative.

Pour les produits et les quotients de trois mesures indépendantes (

R_a

;

R_b

;

R

), on ajoute quadratiquement les incertitudes relatives : précision relative

\sqrt{3} × 0,5 \:%≈0,9 \:%

. Il faut de plus tenir compte des incertitudes sur l'ajustement de la condition d'équilibre du pont, mais avec une boite à quatre décades, l'effet est très faible : on peut considérer au total une incertitude relative

≈1 \:%

.

• On considère ainsi une résistance “inconnue” pour laquelle un ohm-mètre “basique” indique un ordre de grandeur :

R_x=480±50 \:\mathrm{Ω}

.

Par curiosité, on mesure à l'aide de deux ohm-mètres électroniques de précision (

0,2 \:%+1\: \mathrm{digit}

) et on obtient respectivement :

R_x=468±1 \:\mathrm{Ω}

;

R_x=469±1 \:\mathrm{Ω}

.

La connaissance au moins de l'ordre de grandeur sert au choix des résistances du pont (boites étalonnées) :

R_a=R_b=500±1 \:\mathrm{Ω}

.

• L'équilibre du pont (détecté, pour finir, avec un micro-ampèremètre) est obtenu pour

R=471±1 \:\mathrm{Ω}

(boites étalonnées). Ceci donne :

R_x=471±2 \:\mathrm{Ω}

, tout à fait compatible avec les mesures préalables.

• La méthode est ainsi généralement moins précise que l'utilisation directe d'un ohm-mètre électronique de précision (généralement mieux que

≈0,5 \:%

). Mais son but n'est pas là ; l'intérêt est d'être capable de comparer “directement” des résistances, sans avoir besoin pour cela d'un multimètre de précision : cette méthode est capable de mesurer juste même avec un voltmètre (ou ampèremètre) faux... pourvu que son zéro soit correct !

En particulier certains ohm-mètres électroniques de qualité “ordinaire” peuvent donner une indication de résistance approximative quand leur pile est un peu usée : leur conception est basée sur des mesures de tension et leur fonctionnement est parfois perturbé par une tension un peu faible délivrée par leur pile (ceux de bonne qualité le détectent et l'affichent).