EC.II - ÉLECTROCINÉTIQUE - ASSOCIATIONS DE DIPÔLES

1. Association en série

• Les circuits électriques complexes sont constitués de combinaisons de composants simples ; une bonne connaissance de ces dernières facilite l'étude plus générale. Un exemple basique est l'association en série.

• Dans la mesure où le courant est le même dans tout l'assemblage, l'addition des tensions ne dépend pas de l'ordre des composants du modèle.

◊ remarque : les notations de Thévenin sont plus pratiques dans ce cas.

• Quel que soit le courant

I

, les f.e.m. s'ajoutent (par définition).

Par ailleurs, les résistances en série s'ajoutent :

R=R_1+R_2+R_3

U_{AD}=U_{AB}+U_{BC}+U_{CD}=R_1 \:I+R_2 \:I+R_3 \:I=\left(R_1+R_2+R_3 \right) \:I

2. Principe du pont diviseur de tension

• Dans une association de résistances en série (donc parcourues par un même courant), la tension est proportionnelle à la résistance.

I=\frac{U_{AB}}{R_1} =\frac{U_{BC}}{R_2} =\frac{U_{CD}}{R_3} =\frac{U_{AD}}{R_1+R_2+R_3}

Ceci permet de calculer simplement l'une quelconque des tensions à partir de la tension appliquée à l'ensemble ; par exemple :

U_{AB}=\frac{R_1}{R_1+R_2+R_3} \:U_{AD}

3. Loi de Pouillet

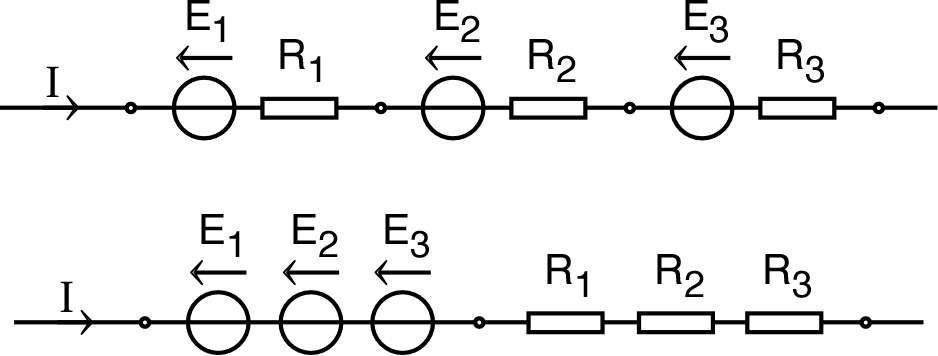
• Pour un circuit simple en série :

∑ \left(±E_i-R_i \:I\right) =0

(d'après la loi des mailles), d'où la loi de Pouillet :

I=\frac{∑ \left(±E_i \right) }{∑ R_i}

◊ remarque : la somme algébrique des

E_i

doit tenir compte de leur convention d'orientation par rapport au sens choisi comme positif ; par exemple, dans le cas ci-contre :

I=\frac{E_1+E_2-E_3}{R_1+R_2+R_3}

4. Association en parallèle

• Dans la mesure où la tension est la même aux bornes de toutes les branches de l'assemblage, l'addition des courants ne dépend pas de l'ordre des composants du modèle.

◊ remarque : les notations de Norton sont plus pratiques dans ce cas.

• Quelle que soit la tension

U_{AB}

, les courants de court-circuit s'ajoutent.

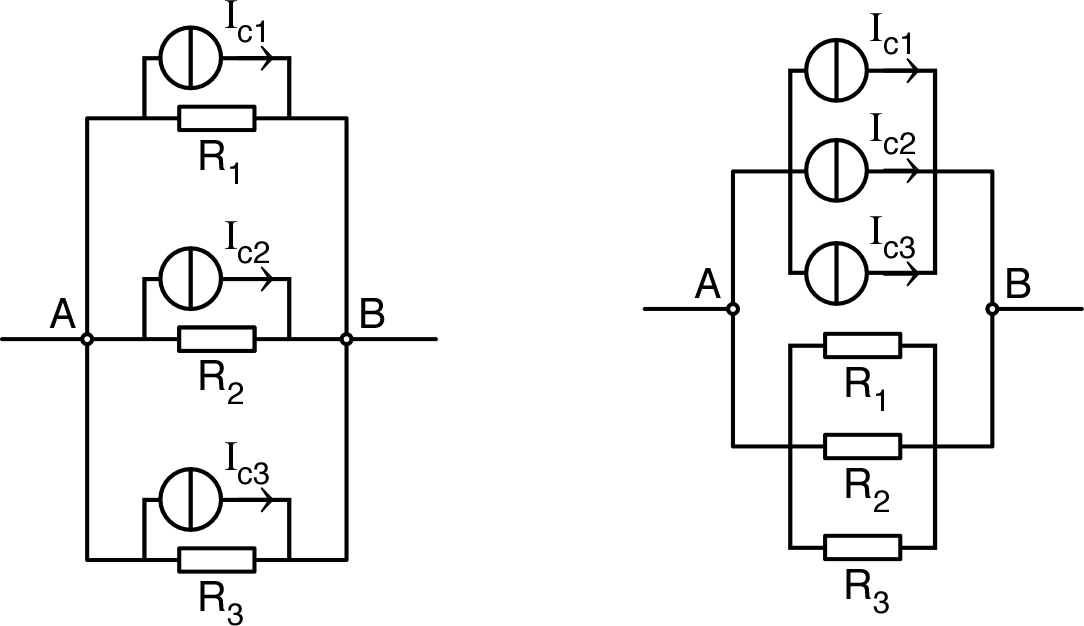
Par ailleurs, les conductances en parallèle s'ajoutent :

G=G_1+G_2+G_3

I=I_1+I_2+I_3

;

I=G_1 \:U_{AB}+G_2 \:U_{AB}+G_3 \:U_{AB}

;

I=\left(G_1+G_2+G_3 \right) \:U_{AB}

5. Principe du pont diviseur de courant

• Dans une association de résistances en parallèle (donc soumises à une même tension), le courant est proportionnel à la conductance.

U_{AB}=\frac{I_1}{G_1} =\frac{I_2}{G_2} =\frac{I_3}{G_3} =\frac{I}{G_1+G_2+G_3}

Ceci permet de calculer l'un quelconque des courants à partir du courant circulant dans l'ensemble ; ainsi :

I_1=\frac{G_1}{G_1+G_2+G_3} \:I=\frac{R_2 R_3}{R_1 R_2+R_2 R_3+R_3 R_1} \:I

6. Loi de Millman

6.1. formulation “basique”

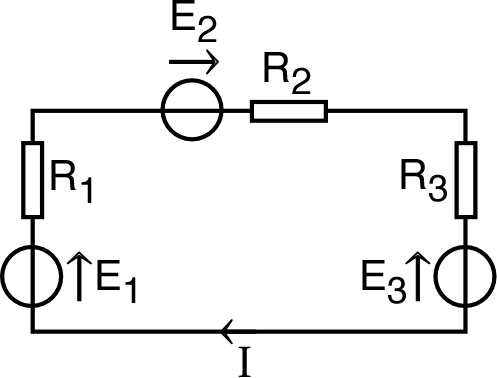
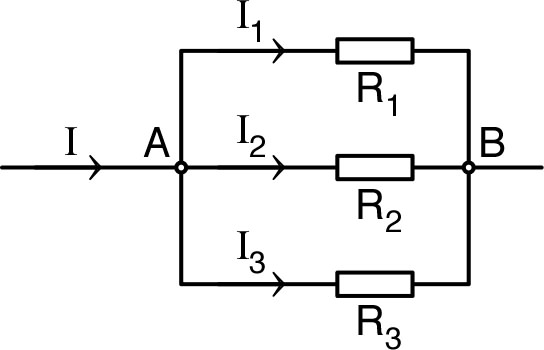
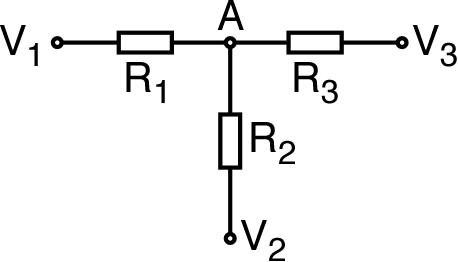
• Pour un circuit simple en parallèle :

∑ \left(±I_{ci}-G_i \:U_{AB} \right) =0

(d'après la loi des nœuds), avec :

±I_{ci}=±\frac{E_i}{R_i}

; d'où la loi de Millman :

U_{AB}=\frac{∑ \left(±I_{ci} \right)}{∑ G_i}=\frac{∑ \left(±\frac{E_i}{R_i} \right) }{∑ \left(\frac{1}{R_i} \right)}

◊ remarque : la somme algébrique des $E_i$ (ou $I_{ci}$ ) doit tenir compte de leur orientation ; par exemple, dans le cas ci-contre : 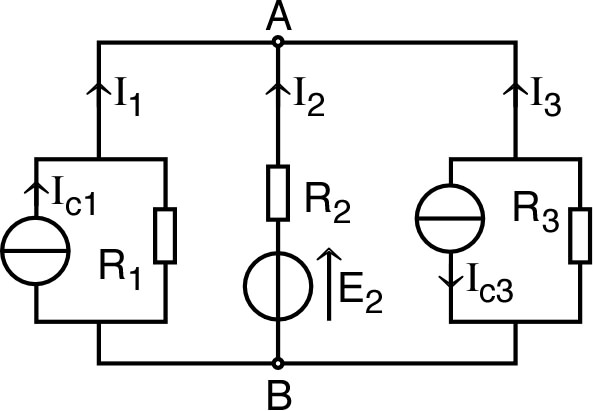$U_{AB}=\frac{I_{c1}+G_2\: E_2-I_{c3}}{G_1+G_2+G_3}$ .

◊ remarque : si l'une des branches correspond à courant fixé (par exemple : générateur de Norton idéal $I_{c1}$ non associé à une résistance $R_1$ ), la relation s'applique en simplifiant simplement ( 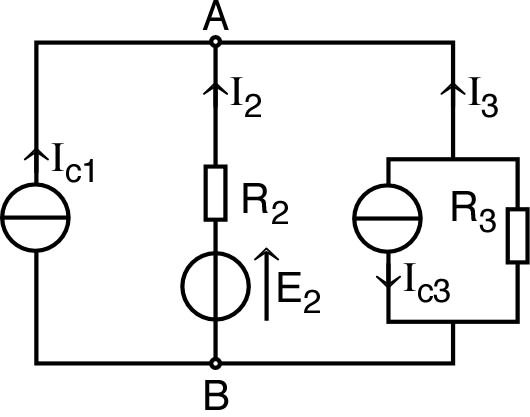$G_1=0$ ) : $U_{AB}=\frac{I_{c1}+G_2 \:E_2-I_{c3}}{G_2+G_3}$ .

6.2. Généralisation de la loi de Millman

• Dans certains circuits, pour lesquels les branches en parallèle n'apparaissent pas de façon évidente, l'utilisation de la loi de Millman peut être facilitée en utilisant comme variables les potentiels.

• On peut ainsi étudier le circuit suivant, en utilisant comme variables les potentiels de nœuds (avec

V_M=0

pour la masse du circuit) :

On suppose que deux générateurs (non représentés) imposent les tensions

U_1=V_{e1}-V_M

U_2=V_{e2}-V_M

; on cherche alors quelle est la tension

U_s=V_s-V_M

en sortie du montage.

☞ indication : le circuit intégré “amplificateur opérationnel” (AO) en fonctionnement linéaire est caractérisé par :

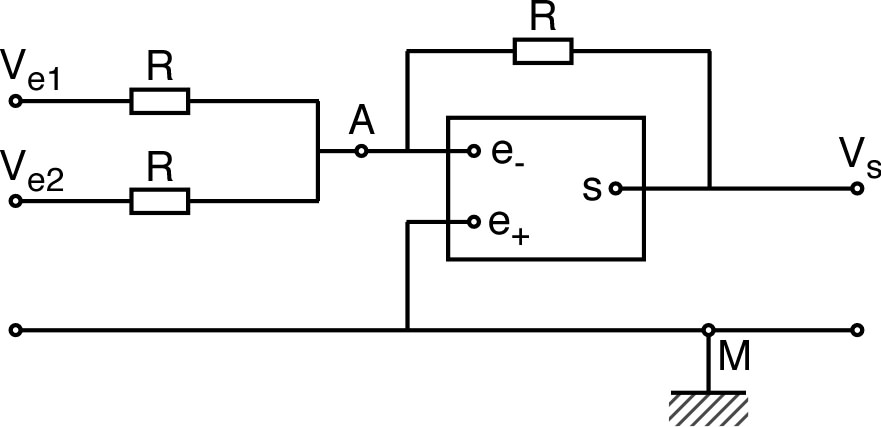
◊	des courants nuls dans les entrées $e_+$ et $e_-$ ;
◊	une tension nulle entre ces entrées ( $V_{e_+}=V_{e_-}$ ).

• La loi de Millman découle de la loi des nœuds, or il ne circule aucun courant dans les entrées de l'AO, donc on peut raisonner (du point de vue des courants) sur le circuit équivalent ci-après qui omet cette connexion.

La loi de Millman donne ainsi :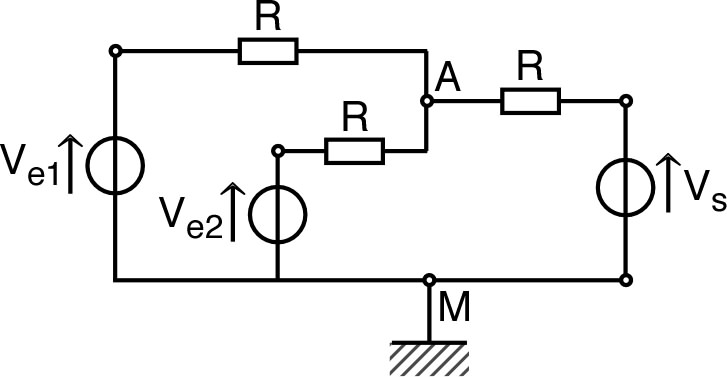

V_A=\frac{\frac{V_{e1}}{R}+\frac{V_{e2}}{R}+\frac{V_s}{R}}{\frac{1}{R}+\frac{1}{R}+\frac{1}{R}}

• Mais par ailleurs, on sait que pour les tensions :

V_A=V_{e_+}=V_{e_-}=V_M=0

; ainsi :

V_s=-\left(V_{e1}+V_{e2} \right)

(le montage est dit “sommateur inverseur”).

• Afin de tirer profit plus facilement de la loi de Millman dans les cas où les schémas équivalents sont moins évidents, on peut alors remarquer que la relation précédente peut s'écrire sous la forme :

V_A=\frac{∑ \left(\frac{V_i}{R_i} \right)}{∑ \left(\frac{1}{R_i} \right)}

📖 exercices n° I, II et III.