• Le second montage est donc équivalent au suivant, dont la branche de droite a pour résistance .
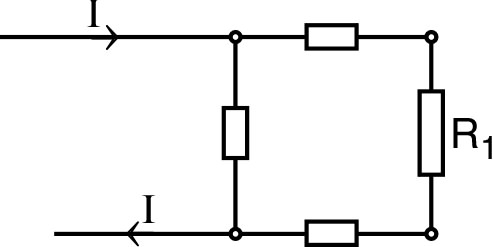
• L'ensemble a donc une résistance telle que : c’est-à-dire : .
| 1.a. | • La résistance de la branche de droite est , donc l’assemblage des deux branches en parallèle a une résistance telle que : c’est-à-dire : . |
| 1.b. | • La maille de droite du second montage est
identique au premier montage, sa résistance est donc
. • Le second montage est donc équivalent au suivant, dont la branche de droite a pour résistance .  • L'ensemble a donc une résistance telle que : c’est-à-dire : . |
| 2.a. | • Pour
branches en parallèle, la résistance de l’ensemble des
branches à droite est
donc l’assemblage des
branches a une résistance
telle que :
c’est-à-dire :
. • Si la limite pour existe, elle est telle que : c’est-à-dire : d’où on déduit : . |
| 2.b. | • On constate que ; ; ; ce qui montre que la suite est très rapidement convergente. |
| 1. | • L'énoncé indique
donc le schéma du générateur correspond à la convention de
signe “usuelle”. Puisque l'électrolyseur est un dipôle
passif, le générateur impose dans les branches de droite un
courant du haut vers le bas, ce qui correspond à
. ◊ remarque : le courant peut être nul si la tension imposée entre ses bornes est insuffisante pour provoquer l'électrolyse. |
| 2. | • Avec les notations de Thévenin, on peut
utiliser le schéma équivalent suivant (où on a aussi
schématisé le montage du rhéostat) :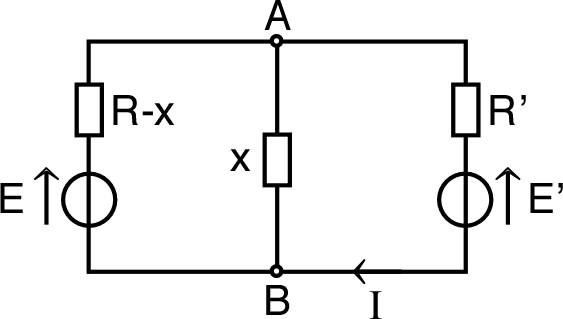 |
| 3. | • La loi de Millmann donne ainsi (s'il y a
électrolyse) :
. • Mais par ailleurs : , donc (tant que cette relation correspond à une valeur positive) : . • La relation précédente est valable pour ; pour on obtient . • On obtient finalement le graphique suivant : 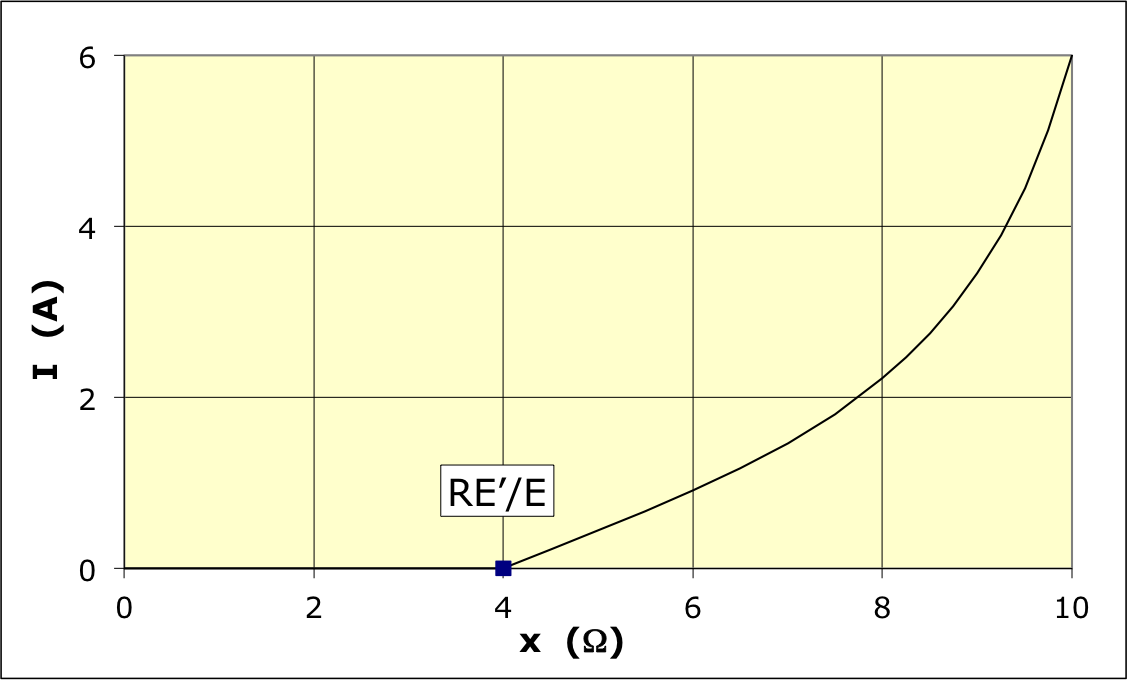 |
| 1. | • Puisque l’interrupteur est ouvert
:
(loi de Pouillet). ◊ remarque : on a alors et la tension aux bornes de l’interrupteur prend automatiquement la valeur : (selon ). |
| 2. | • Quand l’interrupteur est fermé, on peut par
exemple utiliser la loi de Millmann pour calculer la tension
aux bornes de
:
et donc
. On obtient ainsi :
et
(compte tenu de la précision des données). • On peut ensuite calculer par la loi des mailles : . On obtient ainsi : et . • On constate donc que :
|
| |
• La symétrie par rapport au plan passant par , et montre que les courants dans les deux arêtes issues de , autres que , sont égaux ; or leur somme est (loi des nœuds en ), donc ces courants sont égaux à . La symétrie par rotation utilisée précédemment montre alors que les courants dans les six arêtes “intermédiaires” correspondantes sont de même égaux à . • La loi d'Ohm et la loi des tensions donnent alors : . La résistance équivalente de l'ensemble est telle que : c'est-à-dire : . |
| 1. | • Les couples de points symétriques , et sont reliés de façon symétrique, donc le réseau est globalement symétrique par rapport au plan considéré. |
| 2. | • Les points symétriques considérés sont aux mêmes potentiels ; on peut les court-circuiter sans modifier la répartition des courants. |
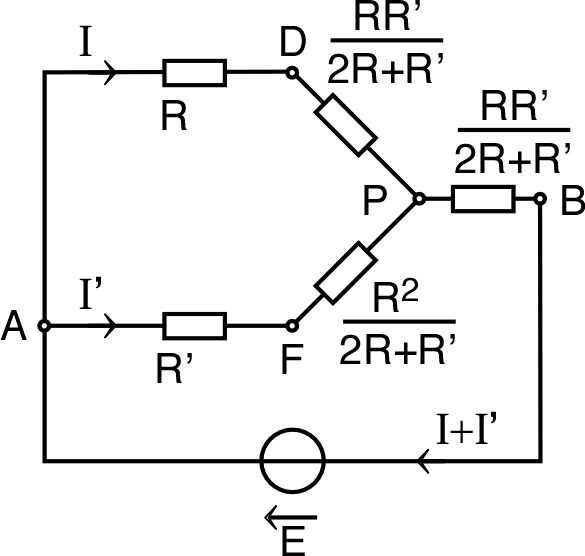
| 3. | • En “aplatissant” le réseau “diagonalement”
(,
et
sont respectivement confondus avec
, et
)
et, en remplaçant chaque paire de résistances en
parallèle par une résistance
, on obtient le réseau équivalent suivant, qui peut
encore se simplifier par des associations en série :
|
| 4. | • Dans un tel réseau, on peut continuer à
simplifier par des équivalences triangle-étoile
(triangles
et
)
; mais, compte tenu de la symétrie centrale et en utilisant
la loi des nœuds, on peut limiter le nombre de courants
inconnus à deux (nombre de mailles indépendantes). • En écrivant la loi des mailles, par exemple pour les deux mailles de gauche, on obtient :
• Ainsi : , d'où la résistance équivalente : . |
| 1. | • L’assemblage de et en parallèle équivaut à : . L’ensemble a donc une résistance de valeur si et seulement si : c’est-à-dire : d’où on déduit : . |
| 2. | • Dans les conditions précédentes
:
et
. • D’après la loi des mailles : donc (en divisant par ) : et par conséquent : . • Compte tenu de la relation initiale : . |
| 3. | • D’après ce qui précède, avec cellules on obtient : et par suite : . |
| 4. | • Par comparaison avec ce qui précède, en remplaçant et (d’où puisque est infinitésimal), la condition est : et donc . |
| 5. | • En posant :
, on obtient :
. • En inversant l’expression de , on obtient par ailleurs : ; en remplaçant on obtient donc : (en limitant au premier ordre puisque est infinitésimal). • Ceci donne : et donc : . Finalement, on aboutit donc à : . |
| 1.a. | • Compte tenu de la loi des nœuds, il suffit
de deux des courant pour décrire le système, par
exemple
et ;
on en déduit alors :
.
|
||
| 1.b. | • D’après la loi des mailles, il suffit de deux des tensions pour décrire le système, par exemple et ; on en déduit alors : . | ||
| 1.c. | • Pour caractériser le tripôle, il est nécessaire et suffisant de savoir calculer les courants qui circulent quand on impose des tensions données, c'est à dire de connaître deux relations donnant deux courants en fonction de deux tensions (ou réciproquement). |
| 2.a. | • Le montage en triangle peut être décrit par
les relations :
|
||||
| 2.b. | • L'inversion donne :
|
||||
| 2.c. | • Le montage en étoile peut être décrit par
les relations :
|
||||
| 2.d. | • Par comparaison : et de même pour et par permutation des indices. |
| 1. | • Le pont de Wheatstone considéré est
électriquement symétrique par rapport au milieu de la
branche car
il comporte la même résistance dans
les branches et
,
ainsi que la même résistance dans
les branches et
. • On en déduit que le même courant (noté ) circule dans les branches et , puis que le même courant (noté ) circule dans les branches et . La loi des nœuds donne les autres courants. ◊ remarque : la symétrie retourne les courants, mais retourne aussi le générateur puisqu'elle intervertit et , donc elle redonne bien le même sens du courant quand on remet le générateur dans le sens initial. |
|
 |