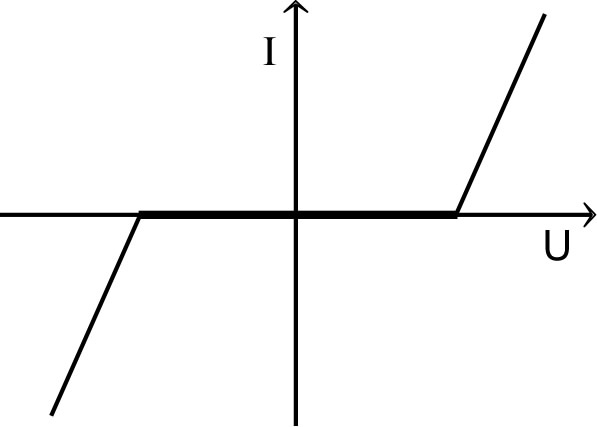ÉLECTROCINÉTIQUE - ASSOCIATIONS DE DIPÔLES

ÉLECTROCINÉTIQUE - ASSOCIATIONS DE DIPÔLES - exercices

A. EXERCICES DE BASE

I. Association de résistances

1. • On considère les circuits suivants, dans lesquels tous les résistors ont la même résistance

r

a) Calculer la résistance équivalente

R_1

du premier circuit.
b) Comparer à

R_1

la résistance de la maille de droite du second circuit. En déduire la résistance équivalente

R_2

de ce dernier.

2. • On considère le circuit suivant (dans lesquels tous les résistors ont la même résistance

r

) comportant un nombre très grand de mailles, symbolisé mathématiquement par (

∞

) :

a) Déterminer la relation “récurrente” entre

R_{n+1}

R_n

; en déduire la résistance équivalente

R

de l'ensemble “infini”.
b) Comparer

R

R_2

II. Électrolyseur

• On considère un électrolyseur (dont la caractéristique est rappelée ci-dessous) branché en sortie d'un montage “diviseur de tension”, avec un générateur de f.e.m.

E=10,0 \:\mathrm{V}

et de résistance interne négligeable, ainsi qu'un rhéostat de résistance

R=10,0 \:\mathrm{Ω}

(au total). On note

x

la résistance de la partie “inférieure” du rhéostat (et donc

R-x

la résistance de la partie “supérieure”).

1. • Quel est le signe du courant (algébrique)

I

dans l'électrolyseur ?

2. • En cours d'électrolyse, l'électrolyseur a une f.c.e.m.

E'=4,0 \:\mathrm{V}

et une résistance

R'=2,0 \:\mathrm{Ω}

. Dessiner un schéma équivalent avec les notations de Thévenin.

3. • Exprimer, en fonction de

x∈[0 \,; R]

, le courant

I

dans l'électrolyseur, puis tracer la courbe représentative de

I(x)

III. Générateurs en opposition

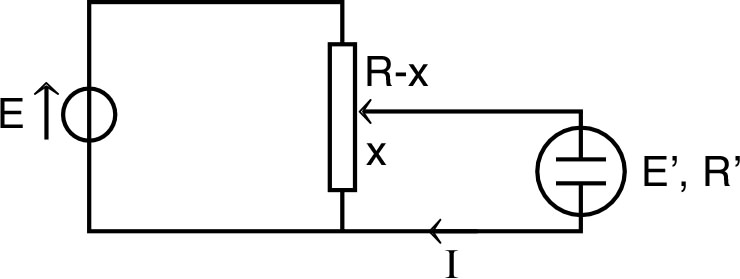
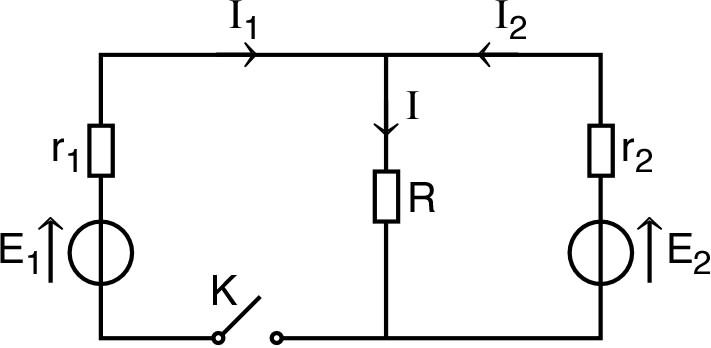
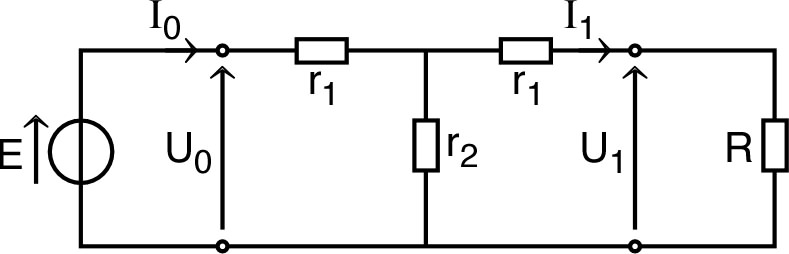
• On considère le montage ci-contre, avec

E_2=12,0 \:\mathrm{V}

E_1=α \:E_2

;

r_1=5,0 \:\mathrm{Ω}

r_2=0,050 \:\mathrm{Ω}

;

R=20 \:\mathrm{Ω}

.

1. • L'interrupteur

K

étant ouvert, calculer le courant

I

dans la résistance

R

2. • On ferme l'interrupteur ; calculer les valeurs

I'

I''

du courant dans

R

pour les deux cas

α'=0,50

α''=1,50

. Calculer les valeurs correspondantes

I_2'

I_2''

; conclure.

B. EXERCICES D’APPROFONDISSEMENT

IV. Association de résistances

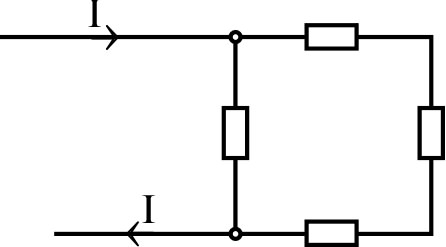
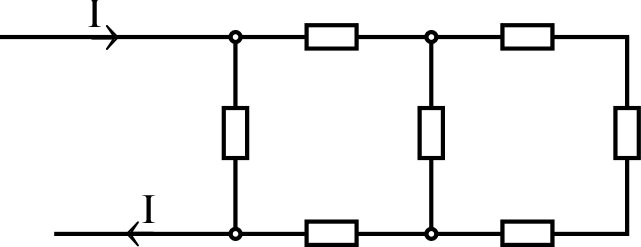
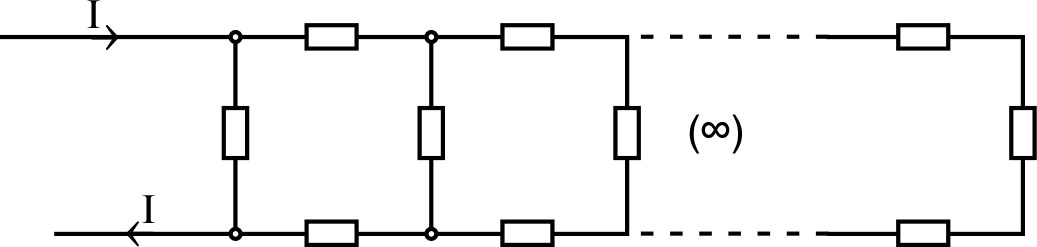
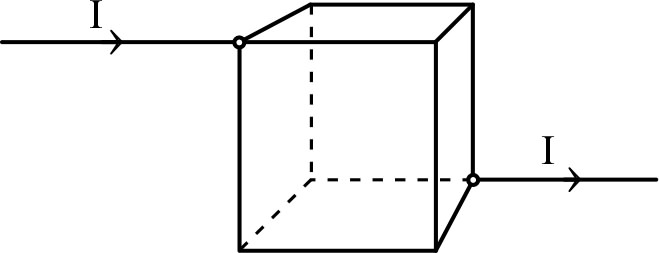
• Les douze arêtes d'un cube sont constituées de fils identiques de résistance

r

.
• Ce cube est relié à un circuit extérieur par deux sommets opposés. Calculer la résistance équivalente de l'ensemble.
☞ indication : en utilisant les symétries, on peut connaître la répartition du courant entre les différentes arêtes.

V. Association de résistances

• On considère le double-cube suivant, dont les vingt arêtes sont constituées de fils identiques de résistance

r

1. • Ce double-cube est relié à un circuit extérieur par deux sommets opposés

A

C''

. Montrer que ce réseau est symétrique par rapport au plan

AA''C''C

.

2. • Justifier qu'on obtient un réseau équivalent en court-circuitant respectivement :

B

D

;

B'

D'

;

B''

D''

.

3. • Simplifier le réseau ainsi obtenu à l'aide des quelques équivalences “série” et “parallèle” mises alors en évidence (il est plus simple de raisonner sur un dessin en projection “à plat” sur le plan

AA''C''C

).

4. • Établir la relation entre la tension

U_{AC''}

et le courant

I

, puis en déduire la résistance équivalente de l'ensemble (on peut encore utiliser les symétries pour préciser la répartition des courants).

VI. Ligne souterraine et résistance itérative

1. • Dans le montage ci-dessous, calculer

R

en fonction de

r_1

r_2

pour que le courant débité par le générateur soit le même que s'il était branché uniquement sur la résistance

R

2. • La résistance

R

étant supposée choisie comme indiqué dans la question précédente, quelles sont les relations entre

U_0

I_0

d'une part, entre

U_1

I_1

d'autre part ? En déduire des expressions de

r_1

r_2

en fonction de

R

α=\frac{U_1}{U_0}

.
Données :

R=1000 \:\mathrm{Ω}

;

α=0,10

.

3. • Calculer

\frac{U_n}{U_0}

si on interpose

n

cellules “en T” identiques à la précédente.

4. • Une ligne souterraine de longueur

L=10 \:\mathrm{km}

, utilisant la terre comme “ligne de retour”, peut être assimilée à une suite en série de cellules “en T” du type précédent.
• Un élément

dx

de ligne peut être représenté par une cellule “en T” avec une résistance

\frac{ρ}{2} dx

à la place de

r_1

(

ρ=0,50 \:\mathrm{Ω.km^{-1}}

est la résistance linéique de la ligne).
• Il y a par ailleurs, entre l'élément de ligne et la terre, un “courant de fuite”

I_f=k \:U \:dx

correspondant à une résistance

\frac{1}{k \:dx}

à la place de

r_2

(

k=3,0.{10}^{-6} \:\mathrm{S.km^{-1}}

est la conductance linéique de fuite de la ligne).
• Quelle résistance de charge

R

faut-il brancher à l'extrémité de la ligne (entre la ligne et la terre) pour que la résistance d'entrée soit indépendante de la longueur de la ligne ?

5. • Pour une longueur de ligne

L=10 \:\mathrm{km}

, calculer le rapport

β=\frac{U(L)}{U(0)}

VII. Équivalence triangle-étoile

1. • Dans la description d'un dipôle électrocinétique intervient un courant et un seul (c'est le même courant qui traverse d'une borne à l'autre) et une tension et une seule (la tension entre les deux bornes). Tout dipôle électrocinétique est caractérisé par une équation reliant le courant qui le traverse et la tension entre ses bornes.

        a) Dans la description d'un tripôle électrocinétique (comme par exemple les tripôles en “triangle” et en “étoile” ci-dessus) peuvent intervenir les trois courants qui passent par les trois bornes. Justifier que deux courants seulement sont indépendants en indiquant la relation qui permet d'en déduire le troisième.
        b) De même peuvent intervenir les trois tensions entre les trois bornes (trois façons d'en choisir deux parmi trois). Justifier que deux tensions seulement sont indépendantes en indiquant la relation qui permet d'en déduire la troisième.
        c) En déduire que tout tripôle électrocinétique est caractérisé par deux équations reliant deux courants qui le traversent et deux tensions entre ses bornes.

2.   a) Dans le montage en triangle, exprimer les courants

I_1

I_2

en fonction des tensions

U_{AB}

U_{AC}

(avec les notations de Norton).
b) Inverser ces relations pour exprimer les tensions

U_{AB}

U_{AC}

en fonction des courants

I_1

I_2

(avec les notations de Norton, puis celles de Thévenin).
c) Dans le montage en étoile, exprimer les tensions

U_{AB}

U_{AC}

en fonction des courants

I_1

I_2

(avec les notations de Thévenin).
d) Par comparaison, en déduire les conditions nécessaires et suffisantes que doivent vérifier les résistances

R_i

R'_i

pour que les deux montages “triangle” et “étoile” soient équivalents.

VIII. Équivalence triangle-étoile

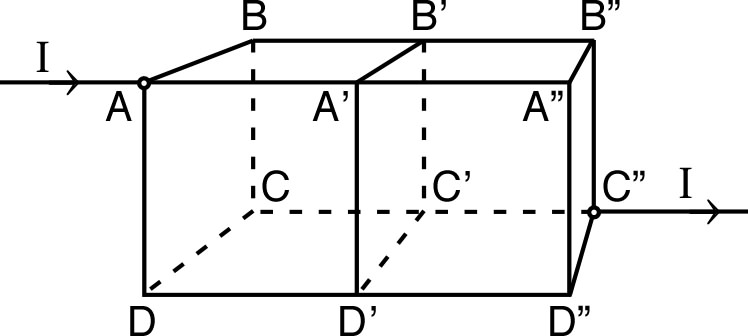
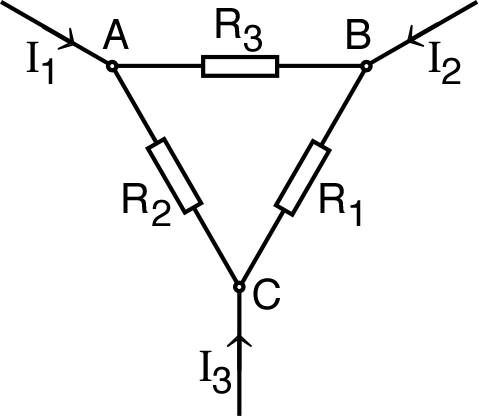
1. • Dans le pont de Wheatstone ci-contre, on désire calculer tous les courants en fonction de la f.e.m.

E

du générateur (et en déduire toutes les tension). Justifier qu'on peut simplifier au préalable les notations en tenant compte des symétries, puis ainsi tout déduire à partir du calcul des deux courants

I

I'

.

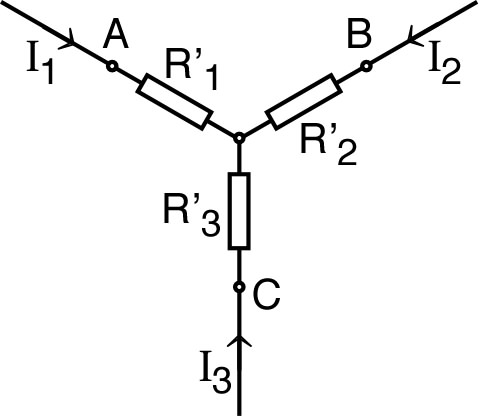
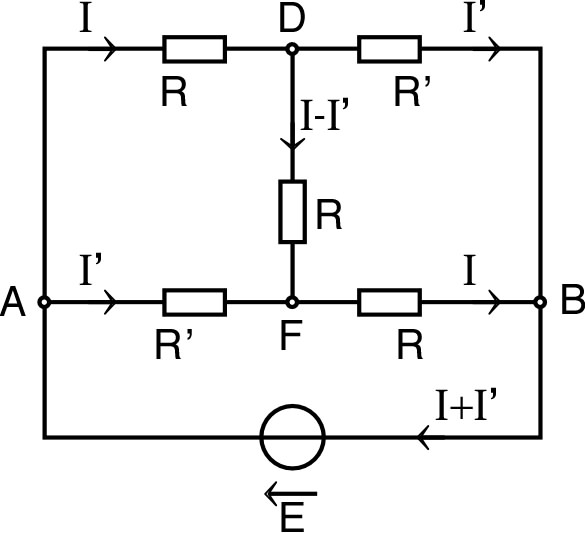
2. • À l'aide d'une équivalence triangle-étoile dans le “triangle”

DFB

(voir l'exercice précédent), trouver un schéma équivalent comportant seulement deux mailles.

3. a) En notant

P

le point central de l'étoile (équivalente)

DFB

, calculer la tension

U_{AP}

.
b) En déduire les courants

I

I'