EC.I - ÉLECTROCINÉTIQUE - LOIS GÉNÉRALES

1. Description d’un réseau électrocinétique

• La représentation d’un réseau physique par des équations mathématiques nécessite de décrire :

◊	comment le réseau est raccordé (à l’aide des lois de Kirchhoff) ;
◊	quels sont les appareils raccordés (on se limite ici à des dipôles).

• On raisonne ici en régime “continu” (tensions et courants constants), mais les principes sont encore valables en régime “lentement” variable.

2. Lois de Kirchhoff

2.1. Loi des nœuds

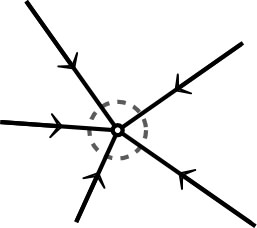
• L'intensité du courant électrique (en ampères) en un point d'un circuit est le débit des charges électriques à travers la “section” du fil en ce point.

◊ remarque : les charges électriques portées par les constituants de la matière sont quantifiées, mais cela n'est pas détectable dans les conditions usuelles car la charge élémentaire est très petite.

◊ remarque : le sens conventionnel algébrique pour chaque courant n'est pas forcément le “sens réel” (qui n'est pas toujours connu) ; un courant  $I$  mesuré dans un sens équivaut à un courant  $-I$  dans l'autre sens.

• En régime (quasi) stationnaire, la conservation de la charge électrique dans un volume délimitant un nœud d'un réseau électrique, conduit à la “loi des nœuds”  (algébrique) :  $\frac{dQ}{dt}=I_{entrant}=∑ \:I=0$ .

2.2. Loi des mailles

• Le potentiel électrique (en volts) en un point d'un circuit est une grandeur qui dépend de l'énergie des charges électriques en ce point.

• En l’absence d’effets magnétiques variables, la tension électrique entre deux points (grandeur mesurée par le voltmètre) est la différence de potentiel entre ces points.

• Cette propriété, appliquée autour d'une maille d'un réseau électrique, a pour conséquence la “loi des mailles”  (algébrique) :  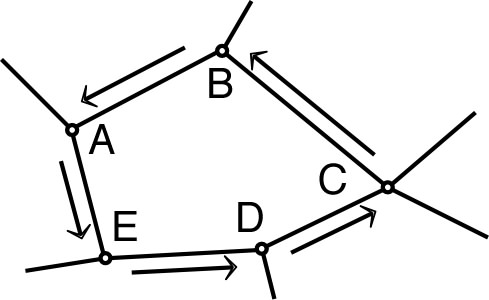$∑\:U=V_A-V_A=0$ .

2.3. Propriétés du système d'équations • Ces équations ne sont pas toutes indépendantes : ◊ la loi des nœuds en D découle de celles en A, B et C ; ◊ la loi des mailles pour ABDCA découle de celles pour ABCA et BDCB.

2.4. Approximation des régimes quasi-stationnaires

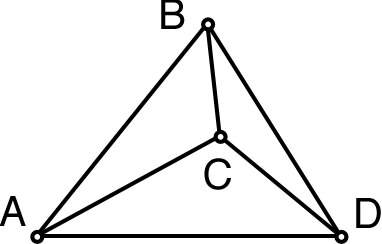• Les lois de Kirchhoff sont applicables en régime continu ou “lentement” variable (ARQS), c'est-à-dire dont les variations sont lentes en comparaison :

◊	des durées microscopiques caractéristiques du milieu (surtout pour les ions, peu mobiles) ;
◊	des durées de propagation électromagnétiques.

Le second effet est prépondérant pour les métaux : sur une distance $≈30 \:\mathrm{cm}$, le délai de propagation (à la vitesse de la lumière) est :  $τ≈{10}^{-9} \:\mathrm{s}$  ;  ceci limite l'étude des régimes périodiques à environ $1 \:\mathrm{GHz}$.

3. Dipôles électrocinétiques en régime continu

3.1. Conventions de notation pour les générateurs

• Pour décrire le fonctionnement caractéristique d'un dipôle, il faut écrire une relation entre le courant qui le traverse et la tension entre ses bornes.

Il faut préciser clairement les sens de mesure algébriques ; par exemple par des indices pour les tensions  ($U_{AB}=V_A-V_B$)  et par des flèches d'orientation des courants sur les branches du réseau.

• Un générateur de tension parfait est tel que :  $U_{AB}=E$  (f.e.m.) quel que soit le courant $I$.

Un générateur de courant parfait est tel que :  $I=I_c$  (courant de court-circuit) quelle que soit la tension $U_AB$.

• À l'arrêt, un générateur de tension parfait est tel que :  $U_{AB}=0$  quel que soit le courant $I$ (court-circuit).

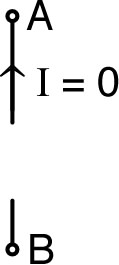À l'arrêt, un générateur de courant parfait est tel que :  $I=0$  quelle que soit la tension $U_{AB}$ (circuit ouvert).

• Pour un générateur quelconque, on peut toujours “linéariser” la caractéristique au voisinage d'un point de fonctionnement $\left(I_0, \,U_0 \right)$ :

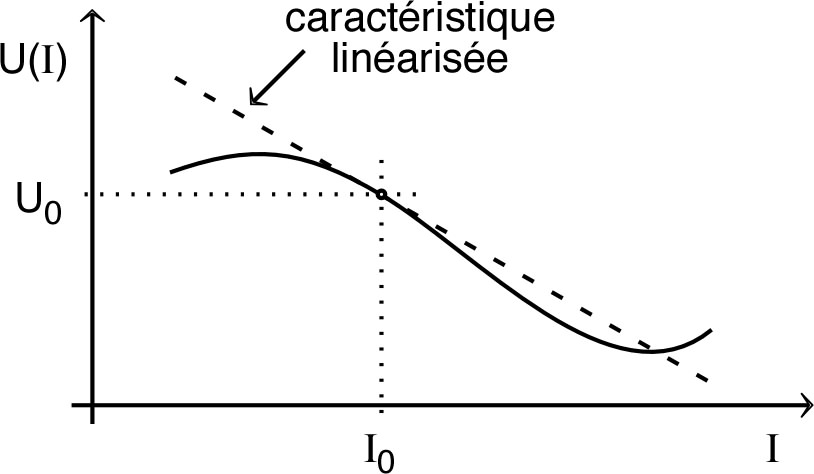
• Avec les notations de Thévenin :  $U\left(I\right)≈U_0 \:\frac{dU}{dI}.\left(I-I_0 \right)$  ;  la caractéristique d'un générateur peut se mettre sous la forme :  $U_{AB}=E-R I$  (convention générateur), en notant :  $R=-\frac{dU}{dI}$    et   $E=U_0+R \:I_0$ .
Avec les notations de Norton :  $I\left(U\right)≈I_0+\frac{dI}{dU}.\left(U-U_0 \right)$  ;  la caractéristique d'un générateur peut se mettre sous la forme :  $I=I_c-G \:U_{AB}$  (convention générateur), en notant 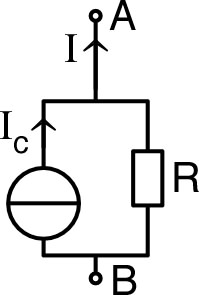:  $G=\frac{1}{R}=-\frac{dI}{dU}$   et   $I_c=G \:E=I_0+G \:U_0$ .

3.2. Conventions de notation pour les récepteurs

• Puisque ces notations sont algébriques, elles s'appliquent aussi aux récepteurs (recevoir de l'énergie consiste à en “fournir” une quantité négative).

On peut au besoin utiliser la notion de force contre électromotrice (f.c.e.m.), qui correspond à une f.e.m. en opposition par rapport au courant.

On obtient ainsi, par exemple, pour une cuve à électrolyse :

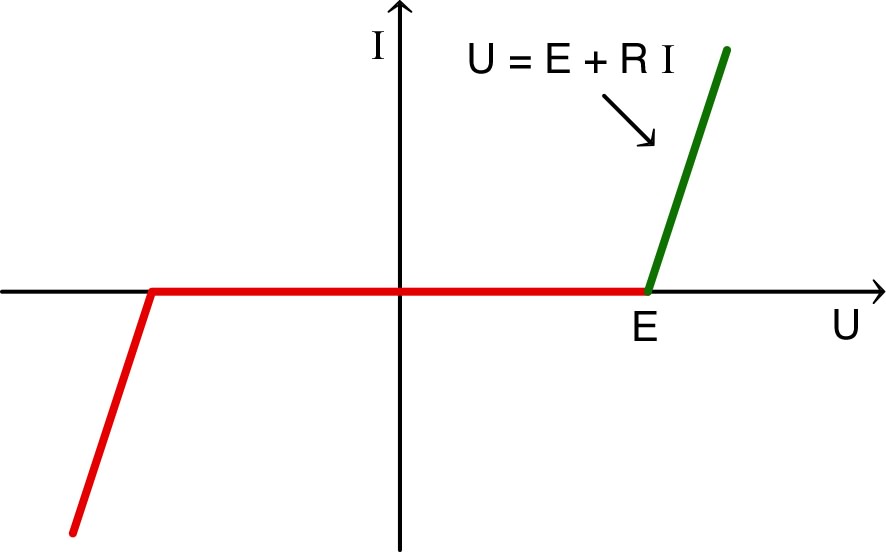• Les lois de la forme :  $U=± E±R \:I$  (où les signes dépendent des conventions arbitraires d'orientation de $U$ et $I$) constituent donc une “loi d'Ohm généralisée” pour tous les dipôles électrocinétiques en régime continu.

4. Point de fonctionnement

• L'association d'un générateur $\{E \,;R\}$ et d'un récepteur $\{E' ;R'\}$ donne un courant  $I=\frac{E-E'}{R+R'}$  mais une méthode graphique permet de trouver le point de fonctionnement même si les caractéristiques ne sont pas linéarisées.

5. Aspects énergétiques ; loi de Joule

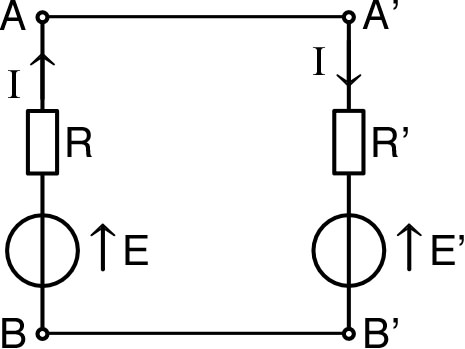• Le travail électrique fourni à une charge  $q>0$  qui traverse une tension $U_{AB}$ est :  $w=-∆E_p=-q \,∆V=q \:U_{AB}$ .

Les charges négatives circulent dans l'autre sens et contribuent au travail avec le même signe :  $w=q\:U_{BA}=\left|q\right| \:U_{AB}$ .

Cette énergie est au fur et à mesure dépensée dans le circuit (pour franchir une f.c.e.m., ou par pertes lors des chocs dus à l'agitation thermique).

Pour l'ensemble des porteurs de charge, cela correspond pendant une durée $δt$ au travail :  $δW = I \:δt \:U_{AB}$  ;  la puissance reçue (algébriquement) par le dipôle est donc :  $𝒫=\frac{δW}{δt}=U_{AB} \:I$  (avec  $I=I_{AB}$).

• Pour un résistor (conducteur ohmique), on retrouve donc ainsi l'effet Joule :  $𝒫=U_{AB} \:I=G \:U_{AB}^{\:\:2}=R \:I^2$,  mais on peut généraliser aux autres dipôles.

Pour un générateur :  $𝒫=U_{BA} \:I=-E \:I+R \:I^2$  (en faisant attention au sens du courant : ici de $B$ vers $A$). Cette puissance reçue est usuellement négative (le générateur fournit une puissance positive) ; mais elle peut être positive si un autre générateur en série impose : ◊ soit  $I<0$  (électrolyse dans un générateur chimique par passage d'un courant “inverse”) ; ◊ soit  $I>I_c$  (plus d’effet Joule que d’énergie générée).
Pour un récepteur :  $𝒫=U_{AB} \:I=E \:I+R \:I^2$  (en faisant attention au sens du courant : de $A$ vers $B$). La partie électrique “utile”  $E \:I$  est alors transformée en autres formes d'énergie (mécanique, chimique...), alors que la partie  $R \:I^2$  est “perdue” par effet Joule.

◊ remarque : pour un dipôle passif, la puissance reçue ne peut pas être négative (bien que la formule semble le permettre dans certains cas) car la modélisation cesse alors d’être valable ; ainsi la relation  $U=E+R \:I$  pour un électrolyseur n’est plus valable pour  $I<0$.

📖 exercices n° I, II, III et IV