ÉLECTROCINÉTIQUE - LOIS GÉNÉRALES - corrigé des exercices


A. EXERCICES DE BASE

I. Caractéristique courant-tension

1. • La puissance dissipée dans le RDT est :  P=UI=CIβ+1P=U \:I=C \:I^{β+1}  et la limite en courant est par conséquent :  IM=(𝒫MC)1β+1=59mAI_M=\left(\frac{𝒫_M}{C}\right)^{\frac{1}{β+1}}=59 \:\mathrm{mA} .
• Le graphique est le suivant :

elCinGen_cor_Im/elCinGen_cor_Im1.jpg


2. • Avec :  U0=CI0βU_0=C \:I_0^{\:β} ,  la caractéristique linéarisée peut s’écrire :  U=U0+(I−I0)∂U∂IU=U_0+\left(I - I_0 \right) \frac{∂U}{∂I} .
• Ceci correspond à :  ∂U∂I=βCIβ−1\frac{∂U}{∂I}=β \:C \:I^{β-1}  ;  E=U0−I0∂U∂I=U0.(1−β)=52,7VE=U_0-I_0 \frac{∂U}{∂I}=U_0 .\left(1-β\right)=52,7 \:\mathrm{V}  (pour  I≈I0I ≈ I_0)  ;  R=βCI0β−1=264ΩR=β \:C \:I_0^{\:β-1}=264 \:\mathrm{Ω}  (pour  I≈I0I ≈ I_0).
◊ remarque : vu la forme de la courbe, on peut considérer que cette approximation affine est assez précise dans tout l’intervalle de 4040 à 60mA60 \:\mathrm{mA} .


3.a. • Le courant de fonctionnement est solution de l'équation :  E′−R′I=CIβE'-R'\:I=C \:I^β.  Cette équation peut être résolue numériquement ; on obtient :  I=49,1mAI=49,1 \:\mathrm{mA}  d'où on déduit :  U=65,7VU=65,7 \:\mathrm{V}.
◊ remarque : on peut vérifier que dans ce cas :  𝒫=UI=3,22W<𝒫M𝒫=U \:I=3,22 \:\mathrm{W}<𝒫_M .


3.b. • En utilisant la caractéristique linéarisée, le courant de fonctionnement vérifie :  E′−RI=E+RIE'-R\:I=E+R \:I  d’où on déduit de même :  I=E′−ER′+R=49,1mAI=\frac{E'-E}{R'+R}=49,1 \:\mathrm{mA}    (l’approximation est donc excellente).


II. Résistance interne et f.e.m. d'un générateur


 • La tension aux bornes du générateur est :  U=E−rIU=E-r \:I.  Si on suppose que la résistance du voltmètre est très grande, le courant II lors de la mesure est négligeable, donc :  E≈U1=240VE≈U_1=240 \:\mathrm{V}.
• Lors de la deuxième mesure :  U2=E−rI=RIU_2=E-r \:I=R \:I   donc :  I=U2R=ER+rI=\frac{U_2}{R}=\frac{E}{R+r}   et   r=RE−U2U2=6Ωr=R \;\frac{E-U_2}{U_2} =6 \:\mathrm{Ω} .


III. Force électromotrice d'un générateur

1. • Pour les générateurs en série dans le même sens, la loi des mailles s’écrit :  E1+E2−RI=0E_1+E_2-R \:I=0  ;  pour les générateurs en série en opposition, la loi des mailles s’écrit :  E1−E2−RI′=0E_1-E_2-R \:I'=0  (en prenant comme sens positif celui correspondant à E1E_1).
• On peut en déduire :  E1+E2E1−E2=II′ \frac{E_1+E_2}{E_1-E_2}=\frac{I}{I'}  ;  puis :  E2E1=I−I′I+I′\frac{E_2}{E_1} =\frac{I-I'}{I+I'} .  On obtient ainsi :  E2=E1I−I′I+I′=1,068VE_2=E_1 \frac{I-I'}{I+I'}=1,068 \:\mathrm{V}  si on suppose que le courant I′I' est dans le sens positif (l’énoncé ne précise pas le sens de mesure) ; on obtient dans le cas contraire  (I′=−0,975mAI'=-0,975 \:\mathrm{mA}) :  E2=E1I−I′I+I′=3,745VE_2=E_1 \frac{I-I'}{I+I'}=3,745 \:\mathrm{V} .


2. • Faute de connaitre les éventuelles corrélations entre II et I′I', l’incertitude sur  α=E2E1α=\frac{E_2}{E_1}   peut s’écrire :  ∆α≈|∂α∂I|∆I+|∂α∂I′|∆I′=2|I|+|I′|(I−I′)2∆I∆α≈\left|\frac{∂α}{∂I}\right|\,∆I+\left|\frac{∂α}{∂I'}\right|\,∆I'=2 \frac{\left|I\right|+\left|I'\right|}{{\left(I-I'\right)}^2} ∆I  (approximation pessimiste). Ceci correspond à une incertitude relative :  ∆αα≈2|I|+|I′|I2−I′2∆I\frac{∆α}{α}≈2 \frac{\left|I\right|+\left|I'\right|}{I^2-{I'}^2} ∆I .
• L’incertitude relative sur  E2=αE1E_2=α \:E_1  peut s’écrire :  ∆E2E2≈∆αα+∆E1E1\frac{∆E_2}{E_2} ≈\frac{∆α}{α}+\frac{∆E_1}{E_1}  (approximation pessimiste) ;  mais aucune incertitude n’est indiquée pour E1E_1 .  D'après la valeur numérique indiquée (nombre de décimales) pour E1E_1, on peut supposer  ΔE1≈0,005VΔE_1 ≈0,01 \:\mathrm{V}  (il semble douteux de la négliger)  ;  ainsi :  ∆E1E1≈2,5.10−3\frac{∆E_1}{E_1} ≈2,5.{10}^{-3}  ;  ∆αα≈4,5.10−3\frac{∆α}{α}≈4,5.{10}^{-3}  ;  ∆E2E2≈7.10−3\frac{∆E_2}{E_2} ≈7.{10}^{-3} .
• On obtient donc :

 ◊ dans le premier cas  (I′=0,975mAI'=0,975 \:\mathrm{mA}) :  E2=1,068±0,007VE_2=1,068±0,007 \:\mathrm{V}  ;

◊ dans le second cas  (I′=−0,975mAI'=-0,975 \:\mathrm{mA}) :  E2=3,745±0,026VE_2=3,745±0,026 V .


IV. Puissance d'un moteur

1. • Le circuit peut être représenté par le schéma suivant, où E′E' est la f.c.e.m. du moteur et où la résistance totale du circuit est  R=r+r′R=r+r' :

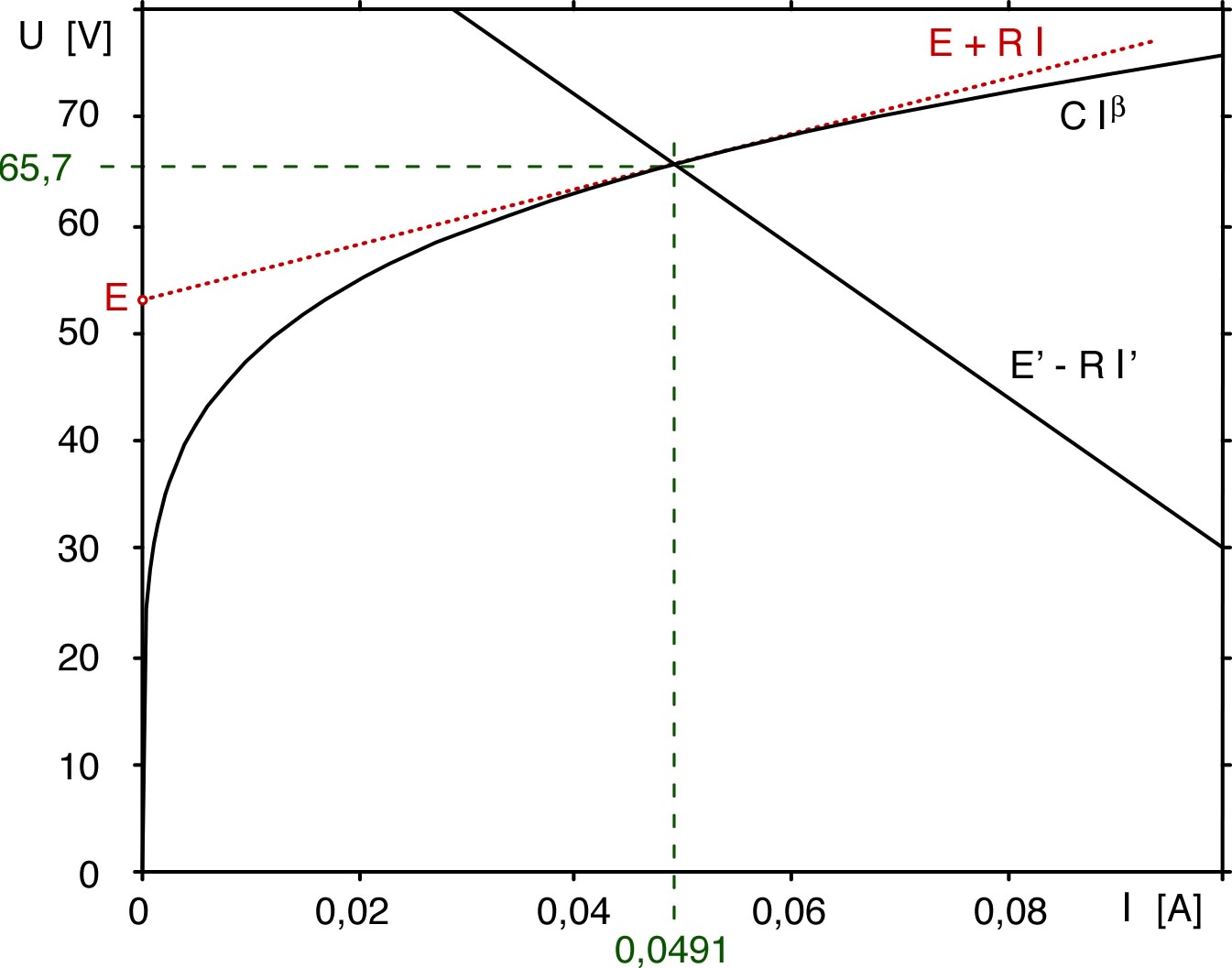
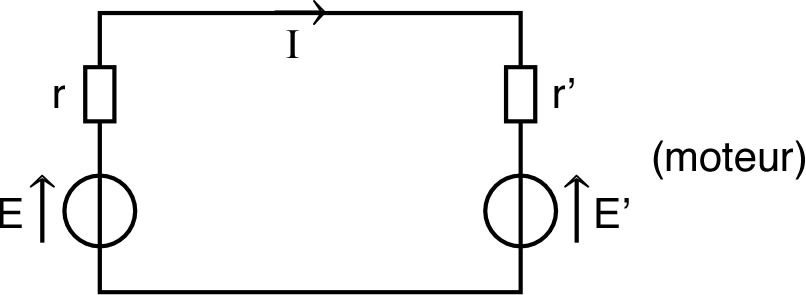elCinGen_cor_Im/elCinGen_cor_Im2.jpg

• La puissance mécanique que peut fournir le moteur est celle (électrique) que reçoit E′E' :  𝒫(I)=E′I𝒫\left(I\right)=E' \:I,  mais E′E' dépend de la vitesse de rotation ωω qui dépend de II de façon non évidente :  E′=E′(ω(I))E'=E'\left(ω\left(I\right)\right).  Par contre, on peut écrire :  𝒫(I)=EI−RI2𝒫\left(I\right)=E \:I-R \:I^2,  expression entièrement définie à partir des données.
• La puissance maximale correspond au maximum de 𝒫(I)𝒫\left(I\right) en fonction de II. La dérivée  d𝒫dI=E−2RI \frac{d𝒫}{dI}=E-2R \:I  s'annule pour  I1=E2R=5AI_1=\frac{E}{2R}=5 \:\mathrm{A} ,  donc la puissance maximum est   𝒫M=𝒫(I1)=E24R=250W𝒫_M=𝒫(I_1 )=\frac{E^2}{4R}=250 \:\mathrm{W} .
◊ remarque : on peut vérifier que  d2𝒫dI2=−2R<0\frac{d^2 𝒫}{dI^2}=-2R<0  ;  il s'agit donc bien d'un maximum.


2. • Le courant II correspondant à :  𝒫(I)=𝒫M2𝒫\left(I\right)=\frac{𝒫_M}{2}  est solution de l'équation :  I2−ERI+E28R2=0I^2-\frac{E}{R \:I}+\frac{E^2}{8\,R^2}=0 ,  ce qui donne :  I=E2R(1±12)I=\frac{E}{2R} \left(1±\frac{1}{\sqrt{2}}\right) .  La valeur inférieure correspond à une puissance mécanique inférieure à 𝒫M𝒫_M pour cause d'insuffisance d'énergie fournie au moteur ; la valeur supérieure correspond à une puissance mécanique inférieure à 𝒫M𝒫_M pour cause de pertes par effet Joule (si, à partir d'un régime donné, on freine mécaniquement le moteur, alors sa f.c.e.m. diminue et II augmente... si cela ne fait pas augmenter la puissance mécanique, c'est que ça fait augmenter l'effet Joule...). La condition "normale" d'utilisation correspond donc à :  I=E2R(1−12)=1,46A<I1I=\frac{E}{2R} \left(1-\frac{1}{\sqrt{2}}\right)=1,46 \:\mathrm{A}<I_1 .
◊ remarque : le courant est :  I=E−E′RI=\frac{E-E'}{R}  (d'après la loi des mailles) ; or, d'après l'indication de l'énoncé, l'utilisation d'une puissance mécanique inférieure à 𝒫M𝒫_M impose "normalement" E′E' supérieure à la valeur correspondant à 𝒫M𝒫_M, donc impose  I<I1I<I_1 .



B. EXERCICES D’APPROFONDISSEMENT

V. Résistance de fuite d'un câble coaxial


 • Si les cylindres ont une résistance non négligeable, correspondant à  adxa \:dx  pour une tranche de longueur dxdx, on peut modéliser une tranche de câble par une résistance  adxa \:dx  “en série” (répartie en deux pour “l’aller” et le “retour”), associée à une résistance  bdx\frac{b}{dx}  “en parallèle”.
• D’après le schéma,  bdx\frac{b}{dx}  représente la “résistance radiale” d’une tranche de câble de longueur  dxdx,  c’est-à-dire que  b=17,5109Ω.mb=17,5{10}^9 \:\mathrm{Ω.m}  représente la “résistance radiale” d’une “unité de longueur” de câble.
◊ remarque : du point de vue du courant radial, les tranches d’épaisseur dxdx s’ajoutent en parallèle ; par suite la “résistance radiale” est proportionnelle à l’inverse de la longueur.
• On peut écrire :  I1=I(x)−I(x+dx)=−dII_1=I\left(x\right)-I\left(x+dx\right)=-dI  ;  ceci implique   U(x+dx)=I1bdx=−bdIdxU\left(x+dx\right)=I_1 \frac{b}{dx}=-b \,\frac{dI}{dx}   mais aussi :  −dU=U(x)–U(x+dx)=aI(x)dx-dU=U\left(x\right)–U\left(x+dx\right)=a \:I\left(x\right) \:dx  et par conséquent   aI(x)=−dUdxa I\left(x\right)=-\frac{dU}{dx} .  Par élimination de II, on obtient :  U(x+dx)=bad2Udx2U\left(x+dx\right)=\frac{b}{a} \,\frac{d^2 U}{{dx}^2}  ,  ce qui correspond à :  d2Udx2−abU=0\frac{d^2 U}{{dx}^2} -\frac{a}{b} \:U=0  (à la fin du calcul, on peut négliger la différence entre  xx  et  x+dxx+dx  en comparaison de la longueur du câble).
• L’intégration de cette équation correspond à :  U(x)=Aeαx+Be−αxU\left(x\right)=A \:e^{αx}+B \:e^{-αx}   avec   α=abα=\sqrt{\frac{a}{b}}  ;  par suite :  I(x)=−1adUdx=−Aαaeαx+Bαae−αxI\left(x\right)=-\frac{1}{a} \frac{dU}{dx}=-\frac{Aα}{a} \:e^{αx}+\frac{Bα}{a} \:e^{-αx}.  Or le courant doit être nul à l’extrémité libre du câble :  I(L)=0I\left(L\right)=0  ;  par suite :  Ae2αL=BA \:e^{2αL}=B  ;  U(x)=A[eαx+eα.(2L−x)]U\left(x\right)=A \:[e^{αx}+e^{α.(2L-x)} ]  ;  I(x)=−Aαa[eαx+eα.(2L−x)]I\left(x\right)=-\frac{Aα}{a} \:[e^{αx}+e^{α.(2L-x)} ] .
• La résistance de fuite est donc :  R0=U(0)I(0)=aα1+e2αLe2αL−1=aαcotanh⁡(αL)=19,1kΩR_0=\frac{U\left(0\right)}{I\left(0\right)} =\frac{a}{α}\, \frac{1+e^{2αL}}{e^{2αL}-1}=\frac{a}{α} \,\mathrm{cotanh⁡}\left(αL\right)=19,1 \:\mathrm{kΩ}.
◊ remarque : dans la limite des petites valeurs de aa, on obtient :  R0=aαcotanh⁡(αL)≈aα2L=bLR_0=\frac{a}{α} \:\mathrm{cotanh⁡}\left(αL\right)≈\frac{a}{α^2 L}=\frac{b}{L} .


VI. Étude d'un électrolyseur

1. • Quand on ferme le circuit, un courant circule qui provoque la polarisation progressive de l’électrolyseur ; ceci correspond à l’apparition d’une f.c.e.m. EE qui tend à s’opposer à E′E' et à diminuer le courant.
• Si  k>1k>1,  la polarisation fait tendre EE vers E0E_0 ; le courant tend alors vers  E′−E0R=(k−1)E0R>0\frac{E'-E_0}{R}=\left(k-1\right) \frac{E_0}{R}>0 .
• Si  k<1k<1,  la polarisation fait tendre EE vers  E′<E0E'<E_0  (E′E' ne peut pas être dépassée car cela nécessiterait un courant en sens inverse, qui ne peut pas être provoqué par le générateur) ; le courant tend alors vers 00.


2. • La loi des mailles donne :  E′−E−RI=0E'-E-R \:I=0 ,  donc pour en déduire une équation sur EE il faut exprimer II en fonction de EE.  L’énoncé indique :  E=E0(1−e−q⁄Q0)E=E_0 \:\left(1-e^{-q⁄Q_0} \right) ,  d’où on déduit :  q=Q0ln⁡(E0E0−E)q=Q_0 \:\ln⁡\left(\frac{E_0}{E_0-E}\right)  et   I=dqdt=Q0E0−EdEdtI=\frac{dq}{dt}=\frac{Q_0}{E_0-E} \,\frac{dE}{dt} .  On obtient donc :  kE0−E=RQ0E0−EdEdtk E_0-E=\frac{R\:Q_0}{E_0-E} \,\frac{dE}{dt}  c’est-à-dire :  dE(E0−E)(kE0−E)=dtRQ0\frac{dE}{(E_0-E)(k \,E_0-E)} =\frac{dt}{R\,Q_0} .
• En décomposant en fonction de EE :  1(E0−E)(kE0−E)=AE0−E+BkE0−E\frac{1}{(E_0-E)(k \,E_0-E) }=\frac{A}{E_0-E}+\frac{B}{k \,E_0-E}  on obtient alors :  A=−B=1(k−1)E0A=-B=\frac{1}{\left(k-1\right) \,E_0 }  et donc :  dEE0−E−dEkE0−E=dt(k−1)E0RQ0\frac{dE}{E_0-E}-\frac{dE}{k \,E_0-E}=dt \:\frac{\left(k-1\right)\,E_0}{R\,Q_0} .
• Ceci s’intègre sous la forme :  ln⁡(|E−E0E−kE0|)=C−αt \ln⁡\left(\left|\frac{E-E_0}{E-k E_0}\right|\right)=C-α \:t  avec  α=(k−1)E0RQ0α=\frac{\left(k-1\right) \,E_0}{R\,Q_0}  et où CC est une constante d'intégration.  D'après les conditions initiales :  C=−ln⁡(k)C=-\ln⁡\left(k\right)  et on obtient :  k|E−E0E−kE0|=e−αtk \:\left|\frac{E-E_0}{E-k \,E_0}\right|=e^{-αt} .
• Il apparaît alors que  ∀t∈ℝ∀\, t∈ℝ :  E≠E0E≠E_0  et  E≠kE0E≠k \,E_0  (en supposant  k≠1k≠1,  il faudrait  |αt|=∞\left|α \:t\right|=∞).  Par suite la quantité  E−E0E−kE0\frac{E-E_0}{E-k\, E_0}  ne change pas de signe ; puisqu’elle vaut initialement  1k>0\frac{1}{k}>0  elle reste toujours positive.  On obtient donc :  kE−E0E−kE0=e−αtk \,\frac{E-E_0}{E-k \,E_0}=e^{-αt}  et finalement :  E=kE01−e−αtk−e−αtE=k \:E_0 \:\frac{1-e^{-αt}}{k-e^{-αt}} .
• Si  k>1k>1,  alors   α>0α>0  et EE tend vers E0E_0 avec un courant limite :  I=E′−E0R=(k−1)E0R>0I=\frac{E'-E_0}{R}=\frac{\left(k-1\right) \,E_0}{R}>0 .
• Si  k<1k<1,  alors  α<0α<0  et EE tend vers  E′=kE0E'=k \,E_0  avec un courant limite :  I=E′−kE0R=0I=\frac{E'-k \,E_0}{R}=0 .
◊ remarque : on retrouve bien ainsi la caractéristique usuelle (affine par morceaux) de l’électrolyseur.