CARACTÉRISTIQUE D’UNE LAMPE À INCANDESCENCE

CARACTÉRISTIQUE D’UNE LAMPE À INCANDESCENCE - corrigé du TP

1. Tracé de la caractéristique

1.1. Tracé point par point

• On effectue les mesures à l’aide d’un ampèremètre et d’un voltmètre ; on les entre dans l’ordinateur pour effectuer les calculs et les graphiques (voir tableau et graphique en annexe).

◊ remarque : on se limite aux valeurs positives car la lampe est symétrique et fonctionne de même dans les deux sens.

elCinGen_corTP1_Im/elCinGen_corTP1_Im2.png

• On constate au premier abord que la tension aux bornes de la lampe, étudiée en fonction de l’intensité du courant, augmente de façon approximativement parabolique.

◊ remarque : la lampe étudiée ici est un modèle

12 \:\mathrm{V}

(plus puissante que pour une “lampe de poche”).

1.2. Tracé “automatique” à l’ordinateur

• Le générateur B.F. utilisé pour faire varier la tension (sinusoïdalement) doit être réglé sur une fréquence :

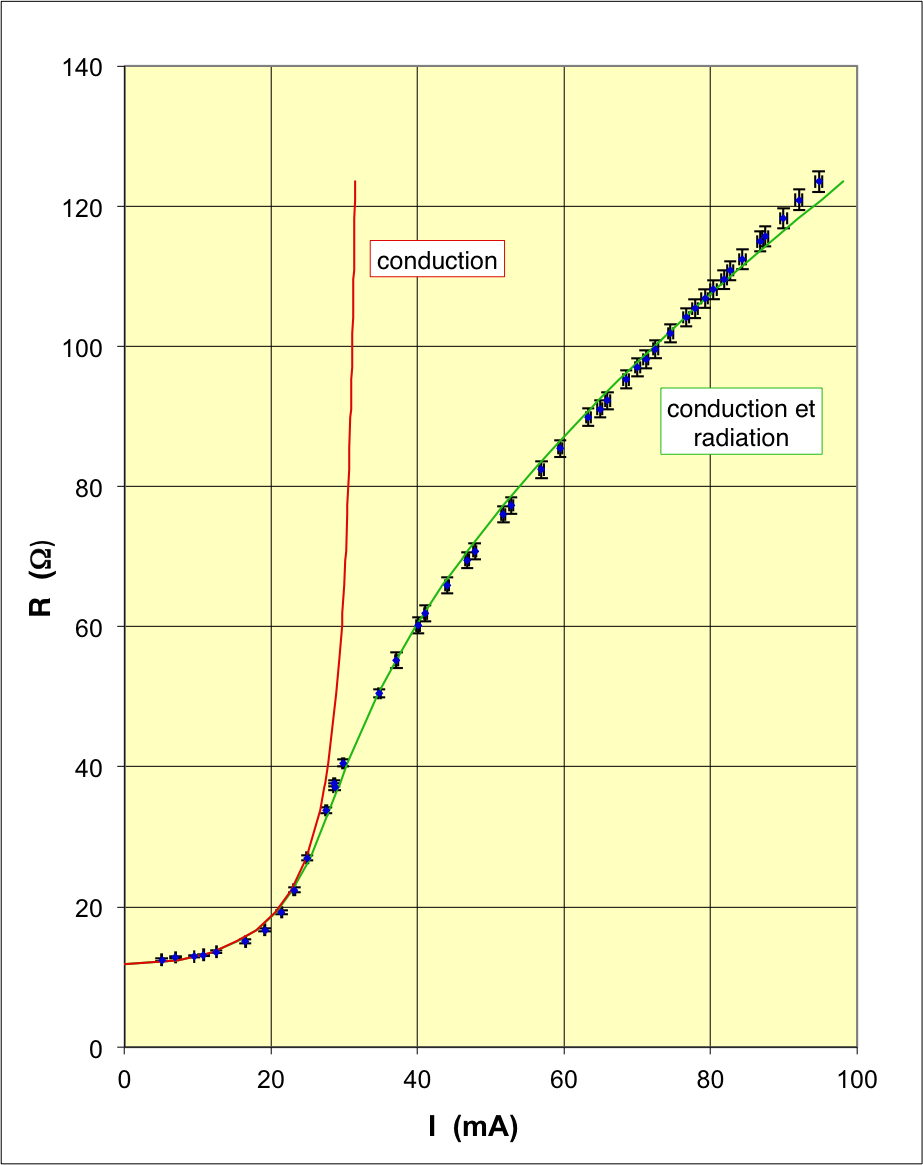
◊	assez grande pour éviter les variations de température dans la durée d’une période ( $N≥10 \:\mathrm{Hz}$ ) ;
◊	assez grande pour éviter le “clignotement” de l’image sur l’oscilloscope ( $N≥50 \:\mathrm{Hz}$ ) ;
◊	assez petite pour éviter que le filament de la lampe (en forme de mini-bobine) ne soit affecté par une auto-inductance parasite ( $N≤80 \:\mathrm{Hz}$ ) ;
◊	telle qu’on évite au mieux les parasites induits par l’effet “d’antenne” (le filament en mini-bobine capte des parasites radio, en particulier les parasites du réseau EDF à $50 \:\mathrm{Hz}$ ) ; le mieux est pour cela de choisir une fréquence de $50 \:\mathrm{Hz}$ pour que les parasites induits se comportent comme l’auto-induction.

On utilise ici une fréquence

N=50,06±0,27 \:\mathrm{Hz}

.

La résistance annexe servant “d’ampèremètre” est par ailleurs

R'=46,35±0,27 \:\mathrm{Ω}

.

• Dans ces conditions, l’observation à l’oscilloscope (en mode XY) de

u\left(t\right)

en fonction de

u'\left(t\right)=R' \:i\left(t\right)

montre une courbe compatible avec une droite passant par l’origine.

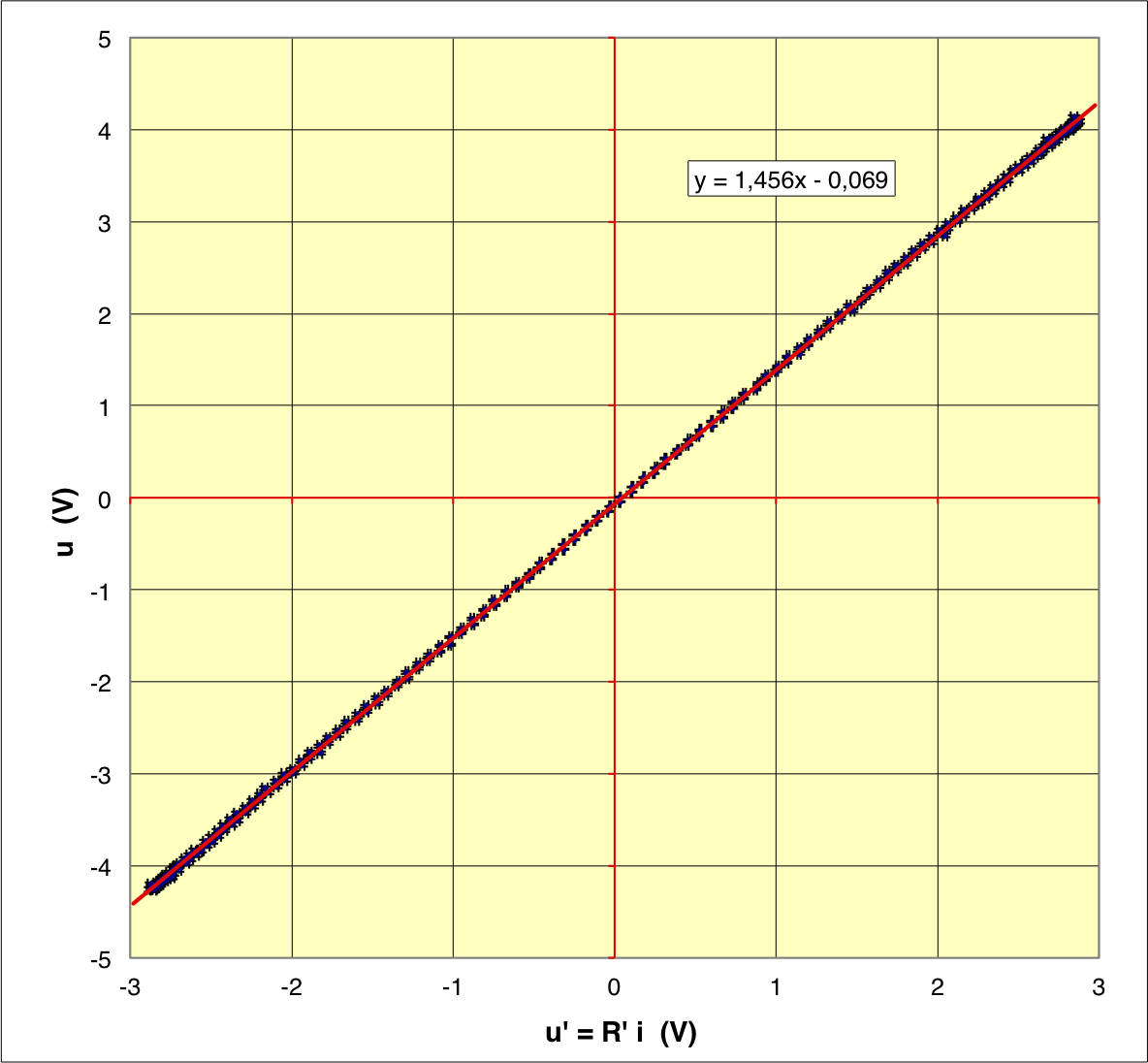
elCinGen_corTP1_Im/elCinGen_corTP1_Im1.png

◊ remarque : pour tracer les graphiques, on enregistre les mesures avec le mode à mémoire de l'oscilloscope puis on les transmet à l’ordinateur (logiciel Synchronie et module Synchroscope), sans oublier de transmettre aussi le zéro des calibres utilisés (les mesures montrées ici, plus anciennes, avaient été obtenues avec une table de mesure connectée à l'ordinateur, mais cela avait l'inconvénient de nécessiter un retraitement des données avant de pouvoir les exploiter).

◊ remarque : l’absence de variation de température et d’effet d’induction est vérifiée s'il y a bien superposition de “l’aller” et du “retour” lors du tracer sur une période (ceci ne peut être observé avec certitude que sur l'écran d'un oscilloscope).

• Puisque la représentation de

u

fonction de

u'

est compatible avec une droite passant par l’origine (caractéristique de la proportionnalité), cela signifie qu’en régime sinusoïdal la lampe se comporte comme un résistor (le filament).

L’ajustement de la pente donne :

\frac{u}{R' \:i}=\frac{R}{R'}=1,456±0,001

c’est-à-dire :

R=67,5±0,5 \:\mathrm{Ω}

(pour une tension maximum

U_m=4,164±0,002 \:\mathrm{V}

soit une tension efficace

U_e=2,944±0,002 \:\mathrm{V}

).

Les incertitudes statistiques calculées ci-dessus sont toutefois optimistes, car un examen attentif montre que l’ordonnée à l’origine n’est pas tout à fait nulle (

-0,069±0,001 \:\mathrm{V}

) ; ceci découle probablement d'une sous-estimation des incertitudes systématiques associées à la transmission des données à l’ordinateur.

• On peut procéder de même pour différentes valeurs de

U_m

et vérifier que les caractéristiques “dynamiques” (mesurées en régime variable) sont dans chaque cas des droites passant par l’origine.

Pour chacune des séries de mesures (les autres séries sont en annexe), la résistance

R

peut alors être déduite simplement du rapport des extremums ou des valeurs efficaces (qu'on peut aussi mesurer directement en ajoutant des voltmètres en parallèle) :

\frac{R}{R'}=\frac{U_m}{U_m'}=\frac{U_e}{U_e'}

.

La comparaison des pentes ainsi obtenues montre que la résistance augmente en fonction de l’intensité efficace du courant (qui provoque une augmentation de la température d’équilibre de la lampe).

2. Modélisations

2.1. Comparaison des caractéristiques “statique” et “dynamiques”

• Chaque caractéristique dynamique étant tracée très rapidement, la température du filament reste constante pendant le tracé, ainsi on observe une caractéristique linéaire :

u=R \:i

où le coefficient de proportionnalité (résistance

R

) dépend de la température

T

à laquelle correspond le tracé :

R=R\left(T\right)

.

Lorsqu’on augmente l’amplitude du signal sinusoïdal, cela augmente la puissance électrique moyenne fournie au filament, ce qui augmente sa température. À cause de l’agitation thermique, la circulation des électrons est alors perturbée et la résistance augmente (la pente des caractéristiques linéaires est d’autant plus grande que l’amplitude et la valeur efficace du signal sont grandes).

• Pour la caractéristique statique, au contraire, chaque point mesuré en régime continu correspond à une température différente. Contrairement aux apparences, l’écriture

U=R \:I

ne correspond alors pas à une proportionnalité car

R

dépend de

T

, qui dépend de

I

, or la fonction :

U\left(I\right)=R\left(T\left(I\right)\right) \:\:I

n’est pas linéaire.

• Sachant que, par définition, les valeurs efficaces d’un régime variable sont les valeurs qu’il faudrait utiliser en régime continu pour obtenir les mêmes effets moyens que le régime sinusoïdal étudié, on peut contrôler les hypothèses précédentes en comparant les deux régimes.

Sur le graphique de

U

fonction de

I

obtenu en régime continu, on reporte ainsi (pour chacune des caractéristiques dynamiques) le point correspondant à

U_e

en fonction de

I_e

. On constate une compatibilité raisonnable, compte tenu des incertitudes plus grandes en régime variable.

◊ remarque : le tracé en régime sinusoïdal ne dépasse pas

U_m≈5 \:\mathrm{V}

à cause de la résistance interne du générateur qui fait “chuter” sa tension dès qu’il débite du courant ; le générateur utilisé (G.B.F.) n'est pas le mieux choisi pour étudier une lampe

12 \:\mathrm{V}

(elle consomme “beaucoup” de courant en comparaison des montages électroniques pour lequel ce générateur est prévu).

◊ remarque : pour comparer les caractéristiques statique et dynamiques, il faut utiliser la même lampe (les caractéristiques varient suffisamment, d’un exemplaire à l’autre du même modèle, pour que la différence soit gênante si on travaille avec des mesures précises).

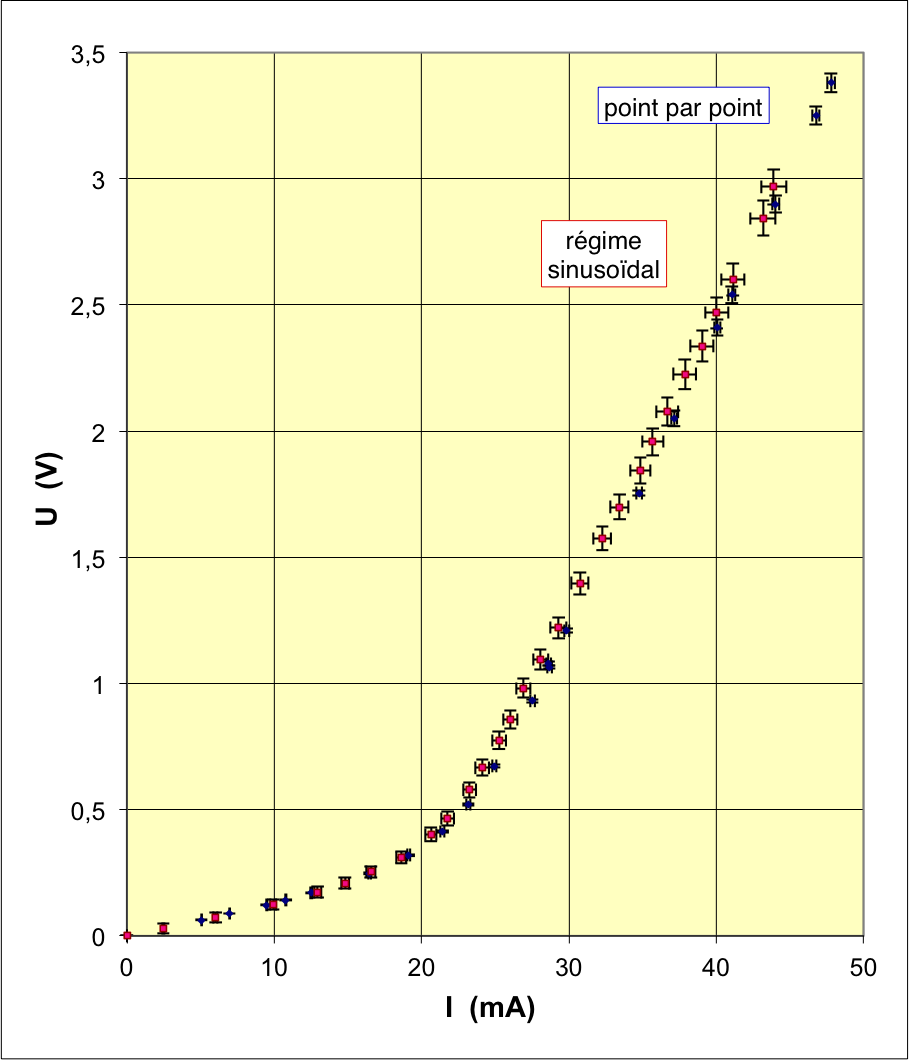
elCinGen_corTP1_Im/elCinGen_corTP1_Im3.png

2.2. Paramétrisation par l’intensité du courant

◊ remarque : dans tout ce qui suit, les données utilisées sont celles mesurées en régime continu car, tout en étant compatibles avec celles déduites du régime variable, elles sont dans l’ensemble d’une précision nettement meilleure.

• Les courbes représentant

U=U\left(I\right)

paraissent approximativement paraboliques ; une interprétation simple consiste à envisager que la résistance augmente de façon affine avec le courant (si

R\left(I\right)

est affine, alors

U=R\left(I\right)\:\,I

est parabolique).

• Le modèle le plus simple (développement limité au premier ordre) consiste à supposer que la résistance varie de façon affine avec la température :

R\left(T\right)≈R_0 .\left[1+α .\left(T-T_0\right)\right]

et que la température varie de façon affine avec le courant

I

T≈T_0 .\left(1+β \:I\right)

; on obtient ainsi :

R\left(I\right)≈R_0 .\left[1+αβT_0 \:I\right]

.

Ce modèle n’est toutefois qu’une très grossière première approximation (voir

R=R\left(I\right)

ci-après) : les points ne sont pas vraiment alignés sur une droite.

Plus précisément on remarque un point d’inflexion caractéristique d’une transition entre deux “régimes” de fonctionnement (incompatibles entre eux) :

	◊ à faible puissance : $R_0=11,75 ±0,15 \:\mathrm{Ω}$ et $αβT_0≈12 \:\mathrm{A^{-1}}$ ;
	◊ à forte puissance : $R_0≈20 \:\mathrm{Ω}$ et $αβT_0≈55 \:\mathrm{A^{-1}}$ .

On pourrait améliorer empiriquement en ajoutant un terme du second ordre dans les développements limités précédents, mais même si l’ensemble des points est un peu moins mal représenté, ceci est assez “artificiel” sans justification physique.

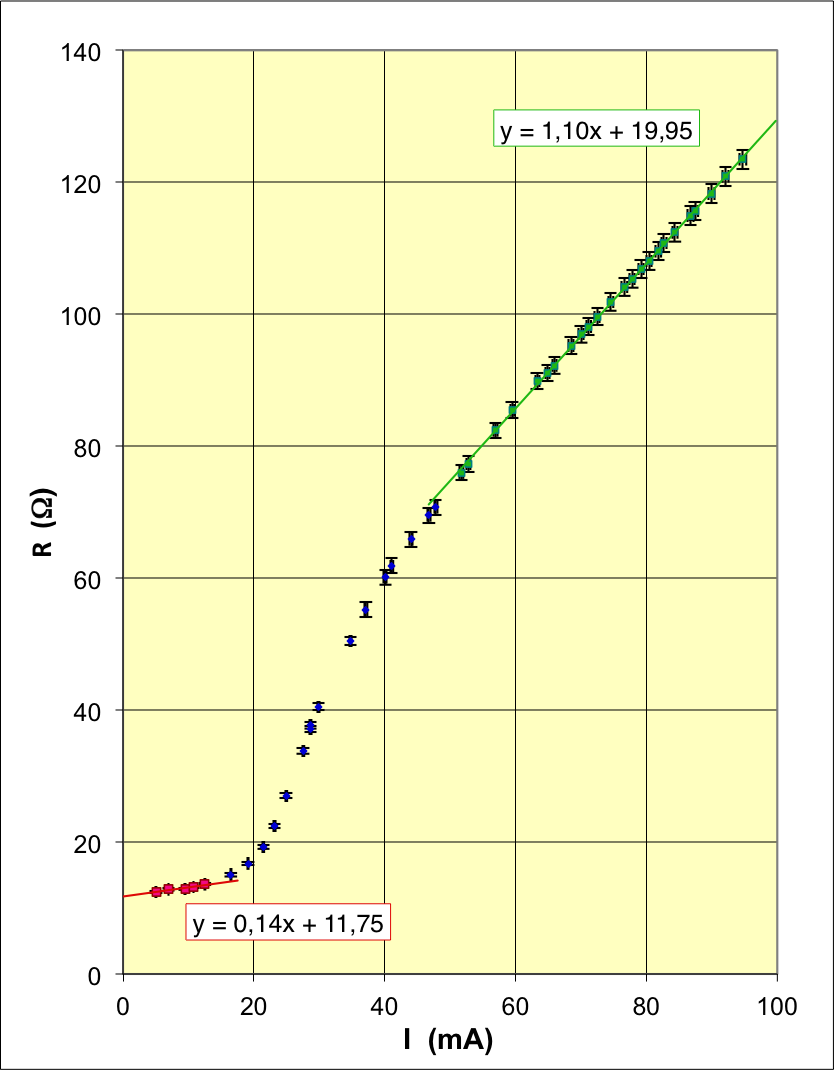
elCinGen_corTP1_Im/elCinGen_corTP1_Im4.png

3. Approfondissement : paramétrisation par la puissance

• L’hypothèse d’une variation affine de

R\left(T\right)

est une bonne première approximation ; par contre, l’hypothèse d’une variation affine de

T\left(I\right)

est trop grossière : la transition précédente entre deux régimes de fonctionnement peut être justifiée par rapport à la puissance électrique.

La loi de Fourier indique qu’en bonne approximation, la puissance thermique transférée par conduction est proportionnelle à la différence de température :

P≈C .\left(T-T_0 \right)

; or, à l’équilibre thermique, cette puissance doit être égale au dégagement par effet Joule :

P=R\left(T\right) \:I^2≈C .\left(T-T_0 \right)

.

On obtient ainsi :

R\left(T\right)≈R_0 .\left[1+α .\left(T-T_0\right)\right]≈R_0 .\left[1+\frac{α}{C} \:R\left(T\right) \:I^2 \right]

d’où on déduit :

R\left(T\right)≈\frac{R_0}{1-\frac{α}{C} \,R_0 \:I^2 }

.

Ce modèle peut sembler problématique dans la mesure où il implique qu’il existe un courant limite pour lequel la résistance devient infinie (et donc de même la puissance thermique). Certes, il est vrai qu’il existe une limite où le fil fond... mais aucune loi physique n’a été prise en compte pour décrire cet effet, donc le modèle ne doit pas y conduire. En réalité, cela provient du fait que la conduction thermique modélisée ici n’est qu’une approximation au premier ordre, limitée aux échauffements modérés.

• Dans la mesure où on connaît expérimentalement la puissance électrique

P=U \:I

de façon assez directe, le mieux est donc plutôt d’essayer d’améliorer le modèle en précisant le lien entre puissance électrique et puissance thermique.

Si on considère comme précédemment

R\left(T\right)≈R_0 .\left[1+α .\left(T-T_0\right)\right]

avec

P≈C .\left(T-T_0 \right)

, on en déduit une variation affine :

R\left(P\right)=R_0 .\left[1+\frac{α}{C} \:P\right]

qui n’est clairement vérifiée que si on se limite aux faibles puissances.

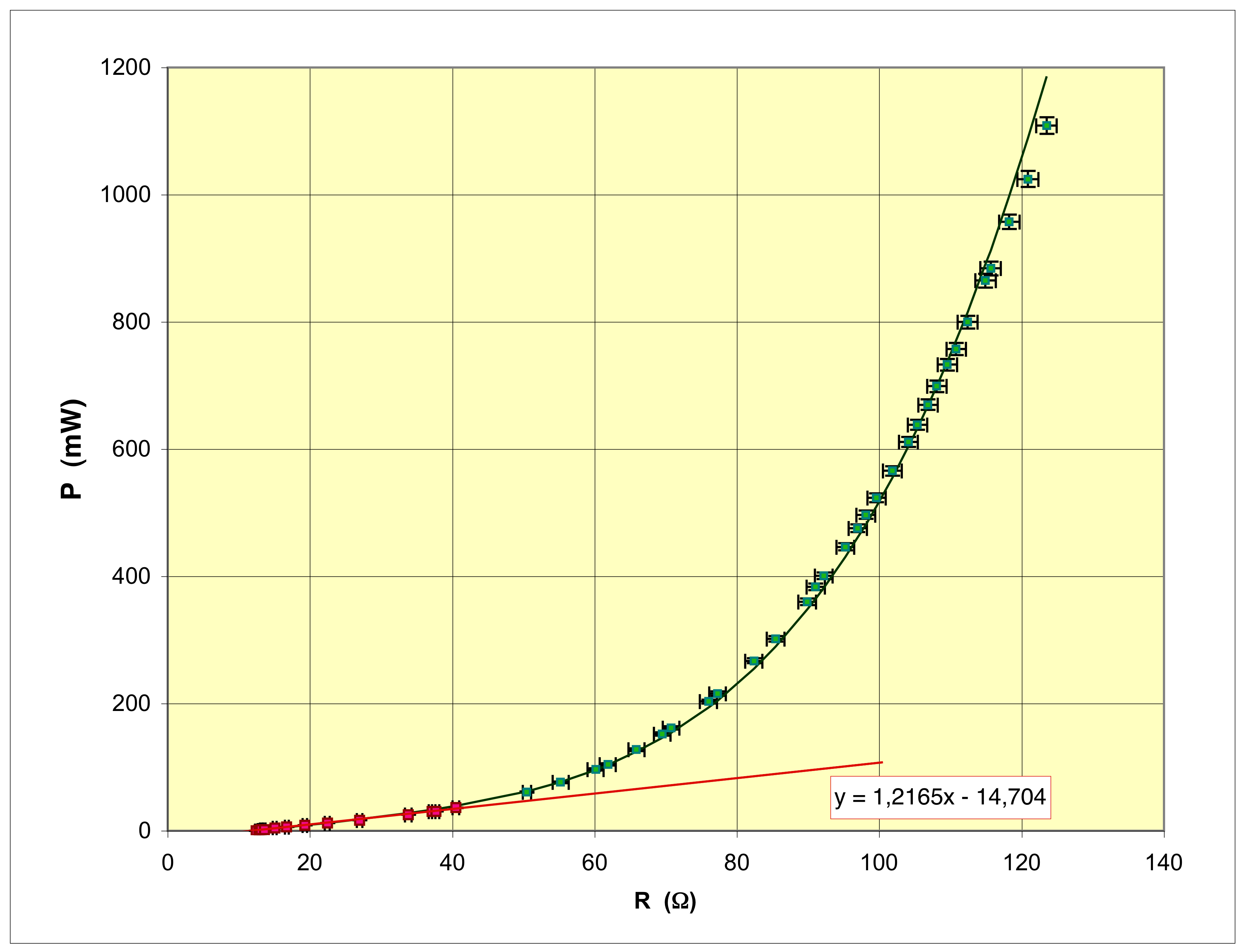
elCinGen_corTP1_Im/elCinGen_corTP1_Im5.png

On peut par contre remarquer qu’il n’y a pas dans ce cas de “brusque” transition entre deux régimes : le prolongement affine du régime des faibles puissances est tangent à la courbe et proche de celle-ci sur toute la partie des puissances “moyennes”. Ceci indique que le choix de la variable

P

est bien adapté à la description des phénomènes physiques qui interviennent ici.

• En fait, la courbe peut être interprétée en tenant compte de la puissance thermique dissipée par rayonnement (dont l’infrarouge, non visible). En effet, s’il est certain que l’énergie rayonnée est négligeable à la température ambiante, elle devient non négligeable quand la température augmente (les chocs dus à l’agitation thermique provoquent des transitions de niveaux électroniques, donc l’émission de photons).

La loi de Stéphan (hors programme) indique que la puissance rayonnée varie selon :

P=D\:T^4

. Puisque la lampe reçoit en contrepartie le rayonnement venant de l’extérieur à la température

T_0

, on peut supposer que la puissance thermique échangée (conduction plus rayonnement) est au total (cette puissance doit s’annuler pour

T=T_0

) :

P≈C .\left(T-T_0 \right)+D .\left(T^4-T_0^{\:4} \right)

.

Ne connaissant pas la température, le mieux est d’utiliser l’hypothèse affine :

R\left(T\right)≈R_0 .\left[1+α .\left(T-T_0\right)\right]

d’où inversement :

θ=T-T_0=\frac{1}{α}∙\left(\frac{R}{R_0} -1\right)

. On en déduit alors en reportant dans l’expression de la puissance :

P\left(θ\left(R\right)\right)=C \:θ+D \:θ∙\left[θ^3+4T_0 \:θ^2+6T_0^{\:2} \:θ+4T_0^{\:3} \right]

.

L’ajustement d’une telle expression est excellent, avec :

R_0=11,84±0,12 \:\mathrm{Ω}

;

αT_0=0,25±0,05

;

\frac{C}{α}=12,9±0,4 \:\mathrm{mW}

;

\frac{D}{α^4} =0,122±0,015 \:\mathrm{mW}

On y remarque que le terme de conduction thermique est effectivement prépondérant tant que la température reste modérée, mais que le terme de radiation devient de plus en plus prépondérant au fur et à mesure que la lampe se met à briller.

◊ remarque : ceci ne signifie pas que la puissance émise sous forme de radiations lumineuses visible est importante (elle est généralement de l’ordre de

10 \,%

seulement), car la majeure partie de l’énergie rayonnée est émise sous forme d’infrarouge (qui est absorbé dans le milieu extérieur).

• Pour vérifier la bonne interprétation de la “transition” entre deux régimes d’équilibre thermique, il est intéressant de reporter ces résultats sur la courbe représentant les variations de

R\left(I\right)

en recalculant (d’après l’effet Joule) :

I\left(P\right)=\sqrt{\frac{P}{R}}

elCinGen_corTP1_Im/elCinGen_corTP1_Im6.png

On constate effectivement qu’en tenant compte de la radiation on retrouve la forme infléchie de la courbe de variation de

R\left(I\right)

, caractéristique de la transition entre deux régimes.

On vérifie en outre qu’avec uniquement la conduction thermique (

D=0

) la résistance tendrait vers l’infini (fusion du filament) pour

I≈\sqrt{\frac{C}{α \,R_0}}≈33 \:\mathrm{mA}

; il en serait de même pour

U\left(I\right)