TRACÉ ET MODÉLISATION DE CARACTÉRISTIQUES

TRACÉ ET MODÉLISATION DE CARACTÉRISTIQUES - corrigé du TP2

1. Caractéristique d’une pile Daniell

• Tout dipôle électrocinétique est caractérisé par une relation entre le courant

I

qui le traverse et la tension

U

entre ses bornes ; cette relation peut être exprimée sous forme d'équation ou sous forme graphique.

• Les dipôles “linéaires” sont ceux dont la relation caractéristique possède des propriétés de linéarité :

U\left(α \:I_1+β \:I_2 \right)=α \:U\left(I_1 \right)+β \:U\left(I_2 \right)

et/ou

I\left(α \:U_1+β \:U_2 \right)=α \:I\left(U_1 \right)+β \:I\left(U_2 \right)

.

Ceci comprend essentiellement les dipôles solutions d'équations différentielles de la forme générale :

∑\left(λ_k \:\frac{d^k U}{{dt}^k}\right) +∑\left(μ_n \:\frac{d^n I}{{dt}^n}\right) =Cste

.

En régime continu, cela se limite à la forme “affine” :

λ \:U+μ \:I=Cste

, généralement notée avec les notations de Thévenin (

U=E-R \:I

) ou de Norton (

I=I_c-G \:U

) .

◊ remarque : en régime variable, la forme plus générale peut se ramener à cette notation plus simple si on utilise des représentants complexes.

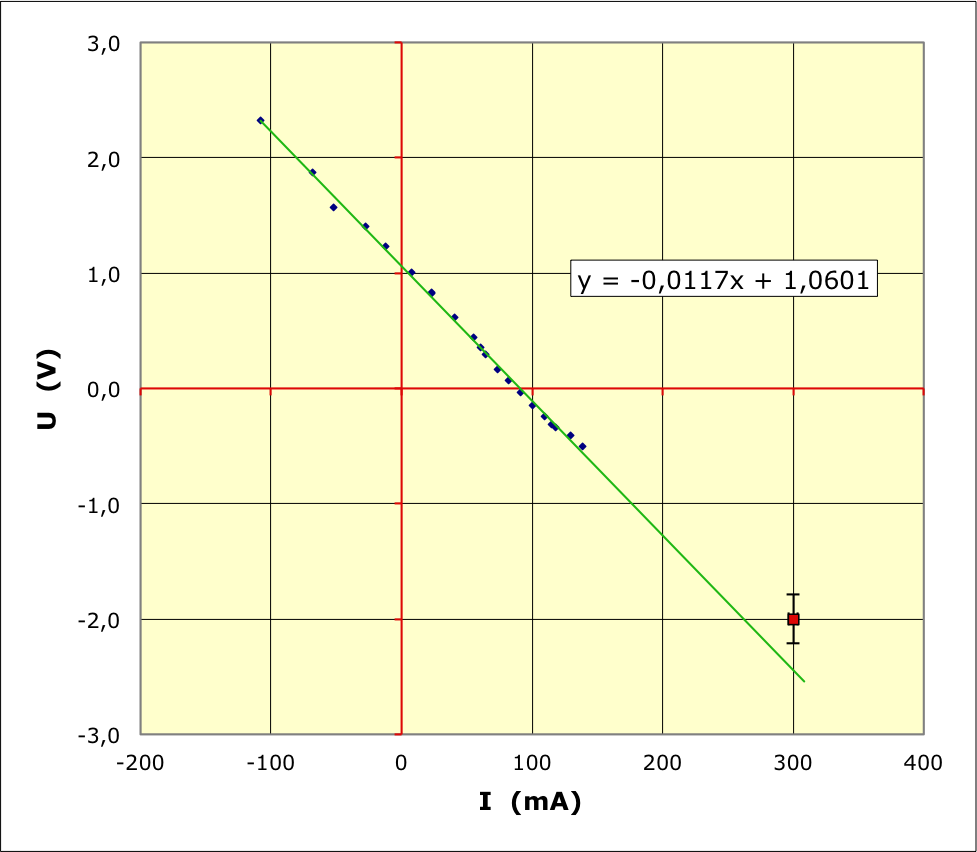
2. Tracé de la courbe “caractéristique” point par point

• Le tracé de la caractéristique montre qu'on obtient en assez bonne approximation une droite ne passant pas par l'origine (forme affine). Le fonctionnement correspondant peut être interprété en trois parties.

elCinGen_corTP2_Im/elCinGen_corTP2_Im1.png

• Pour

U>E

les électrodes sont à des potentiels

V\left(\mathrm{Cu}\right)>E^0 \left(\mathrm{Cu}^{2+}/ \mathrm{Cu}\right)

V\left(\mathrm{Zn}\right)<E^0 \left(\mathrm{Zn}^{2+}/ \mathrm{Zn}\right)

; ceci provoque l'oxydation des atomes de cuivre de l'électrode (qui passent en solution sous forme d'ions

\mathrm{Cu}^{2+}

) et la réduction des ions zinc de la solution (qui se déposent sur l'électrode de zinc sous forme d'atomes

\mathrm{Zn}

). Ceci correspond à une recharge de la pile.

L'électrode

\mathrm{Cu}

est donc l'anode (par définition : borne par laquelle entre le courant, ce qui est associé à une oxydation) et l'électrode

\mathrm{Zn}

est la cathode (par définition : borne par laquelle sort le courant, ce qui est associé à une réduction). Le courant

I

est ainsi négatif (en convention générateur).

L'électrode de cuivre peut être qualifiée de “borne (+)” et l'électrode de zinc de “borne (-)” puisque cela correspond à l'ordre de leurs potentiels :

V\left(\mathrm{Cu}\right)>V\left(\mathrm{Zn}\right)

pour

U>0

.

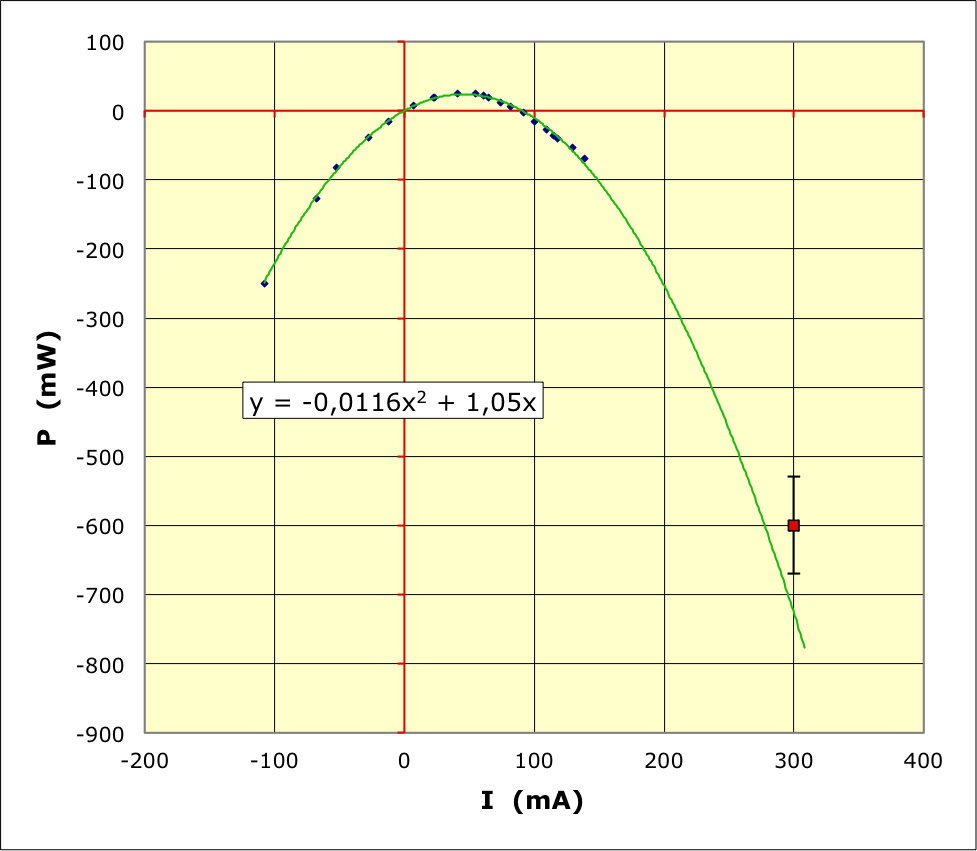
En convention générateur, la puissance électrique fournie par la pile au circuit est :

P=U \:I=E \:I-R \:I^2<0

(

-P>0

est reçue par la pile). La puissance “générée” est

E \:I<0

(dans ce cas

-E \: I

correspond à de l'énergie électrique transformée en énergie chimique : recharge de la pile) ; la puissance consommée par effet Joule correspond à

-R \:I^2<0

(énergie “perdue” dans la pile, non disponible pour la recharge).

elCinGen_corTP2_Im/elCinGen_corTP2_Im2.png

• Pour

0<U<E

les électrodes sont à des potentiels

V\left(\mathrm{Cu}\right)<E^0 \left(\mathrm{Cu}^{2+}/ \mathrm{Cu}\right)

V\left(\mathrm{Zn}\right)>E^0 \left(\mathrm{Zn}^{2+}/ \mathrm{Zn}\right)

; ceci provoque l'oxydation des atomes de zinc de l'électrode (qui passent en solution sous forme d'ions

\mathrm{Zn}^{2+}

) et la réduction des ions cuivre de la solution (qui se déposent sur l'électrode de cuivre sous forme d'atomes

\mathrm{Cu}

). Ceci correspond à une décharge de la pile.

L'électrode

\mathrm{Zn}

est donc l'anode (par définition : borne par laquelle entre le courant, ce qui est associé à une oxydation) et l'électrode

\mathrm{Cu}

est la cathode (par définition : borne par laquelle sort le courant, ce qui est associé à une réduction). Le courant

I

est ainsi positif (en convention générateur).

L'électrode de cuivre peut être qualifiée de “borne (+)” et l'électrode de zinc de “borne (-)” puisque cela correspond à l'ordre de leurs potentiels :

V\left(\mathrm{Cu}\right)>V\left(\mathrm{Zn}\right)

pour

U>0

.

En convention générateur, la puissance électrique fournie par la pile au circuit est :

P=U \:I=E \:I-R \:I^2>0

. La puissance “générée” est

E \:I>0

(dans ce cas

E \: I

correspond à de l'énergie chimique transformée en énergie électrique : décharge de la pile) ; la puissance consommée par effet Joule correspond à

-R \:I^2<0

(une partie de l'énergie générée est “perdue” et non transmise au circuit).

• Pour

U<0

les électrodes sont à des potentiels

V\left(\mathrm{Cu}\right)<E^0 \left(\mathrm{Cu}^{2+}/ \mathrm{Cu}\right)

V\left(\mathrm{Zn}\right)>E^0 \left(\mathrm{Zn}^{2+}/ \mathrm{Zn}\right)

; ceci correspond encore à une décharge de la pile, mais dans des conditions “anormales” : sur-décharge forcée par le générateur annexe (très forcée pour

U=-2 \:\mathrm{V}

).

L'électrode

\mathrm{Zn}

est donc l'anode (par définition : borne par laquelle entre le courant, ce qui est associé à une oxydation) et l'électrode

\mathrm{Cu}

est la cathode (par définition : borne par laquelle sort le courant, ce qui est associé à une réduction). Le courant

I>I_c

est ainsi positif (en convention générateur).

L'électrode de cuivre peut être qualifiée de “borne (-)” et l'électrode de zinc de “borne (+)” puisque cela correspond à l'ordre de leurs potentiels :

V\left(\mathrm{Cu}\right)<V\left(\mathrm{Zn}\right)

pour

U<0

.

En convention générateur, la puissance électrique fournie par la pile au circuit est :

P=U \:I=E \:I-R \:I^2<0

(

-P>0

est reçue par la pile et gaspillée en effet Joule). La puissance “générée” est

E \:I>0

(dans ce cas

E \:I

correspond à de l'énergie chimique transformée en énergie électrique : décharge de la pile gaspillée en effet Joule) ; la puissance consommée par effet Joule correspond à

-R \:I^2<-E \:I<0

(plus d'énergie “perdue” que d'énergie générée).

3. Mesure d’une f.e.m. par la méthode d’opposition

• La caractéristique obtenue précédemment correspond à :

E=1,060±0,015 \:\mathrm{V}

;

R=11,7±0,1 \:\mathrm{Ω}

;

I_c=90,6±0,2 \:\mathrm{mA}

;

G=85,5±0,2 \:\mathrm{S}

.

La mesure de la f.e.m. par méthode d'opposition est en attente de données fournies par les étudiants...