EC.I.a - ÉLECTROCINÉTIQUE - LOIS LOCALES



1. Charges et courants

1.1. Densité de courant

• Dans les conditions statiques, les particules (quasi-ponctuelles) portant des charges électriques ne sont par immobiles, mais animées de mouvements d'agitation thermique ; toutefois leur vitesse moyenne est nulle :  ⟨v→⟩=0→\left⟨\overset{→}{v} \right⟩=\overset{→}{0} .

Le courant électrique correspond à un léger mouvement d'ensemble : avec  ‖⟨v→⟩‖≈10−5m.s−1\left‖\left⟨\overset{→}{v}\right⟩\right‖≈{10}^{-5} \:\mathrm{m.s^{-1}} ,  alors que  ⟨‖v→‖⟩≈500m.s−1\left⟨\left‖\overset{→}{v} \right‖\right⟩≈500 \:\mathrm{m.s^{-1}} .

Dans de très nombreux raisonnements, on peut toutefois négliger l'agitation thermique et considérer uniquement les vitesses moyennes “locales”, avec la même précision qu'on représente un ensemble de charges ponctuelles par une charge volumique (ou densité volumique de charge) :  ρ=δqδ𝒱ρ=\frac{δq}{δ𝒱} .

◊ remarque : les moyennes doivent être calculées sur des volumes δ𝒱δ𝒱 qui sont à la fois assez grands au niveau microscopique, pour supprimer les fluctuations liées à l'agitation thermique, mais petits au niveau macroscopique, pour permettre la description de phénomènes non uniformes à notre échelle (pour décrire des phénomènes variables dans le temps, il faut de même raisonner sur des intervalles de temps appropriés).

• Pour décrire en détail le courant électrique, le nombre des charges mobiles et leur vitesse moyenne “locale” peuvent dépendre de la portion de conducteur considérée.

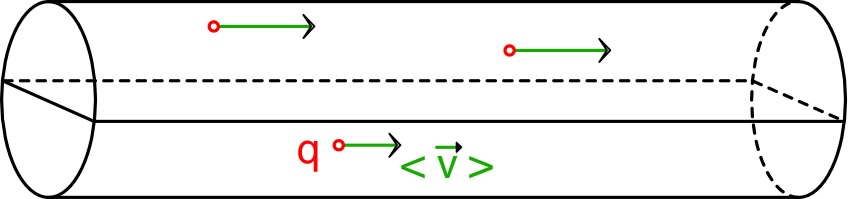
elCinLoc_Im/elCinLoc_Im1.jpg

Ainsi, pour un conducteur cylindrique formé de deux matériaux différents, si les charges se “déplacent plus” dans la partie supérieure (plus nombreuses et/ou plus rapides), la contribution au courant total y est plus grande.

On peut alors définir (dans ce cas particulier simple) la “densité” de courant comme le “courant par unité de surface” à travers chaque partie de la section du conducteur :  j=δIδSj=\frac{δI}{δS}  (unité de base : A.m−2\mathrm{A.m^{-2}}).

• Il est également utile de décrire l'orientation “locale” du mouvement moyen des charges (vecteur ⟨v→⟩\left⟨\overset{→}{v} \right⟩). Mais plus précisément, il faut exprimer l'orientation “locale” de l'effet de ce mouvement sur le courant : direction et sens de  q⟨v→⟩q \:\left⟨\overset{→}{v} \right⟩  (s'il n'y a qu'une sorte de porteurs de charge).

Selon cette orientation, une charge  dQdQ  qui traverse une surface infinitésimale dS→d\overset{→}{S} pendant un intervalle de temps  δtδt  est :  dQ=j→∙dS→δtdQ=\overset{→}{j}∙d\overset{→}{S} \:δt  avec  j→=ρ⟨v→⟩\overset{→}{j}=ρ \:\left⟨\overset{→}{v}\right⟩ .  En effet, la contribution des charges qq ayant une vitesse moyenne ⟨v→⟩\left⟨\overset{→}{v}\right⟩ peut s'écrire :  dQ=ρdτdQ=ρ \:dτ  avec un volume infinitésimal  dτ=d𝓁→∙dS→=⟨v→⟩∙dS→δtdτ=d\overset{→}{𝓁}∙d\overset{→}{S}=\left⟨\overset{→}{v}\right⟩∙d\overset{→}{S} \:δt .

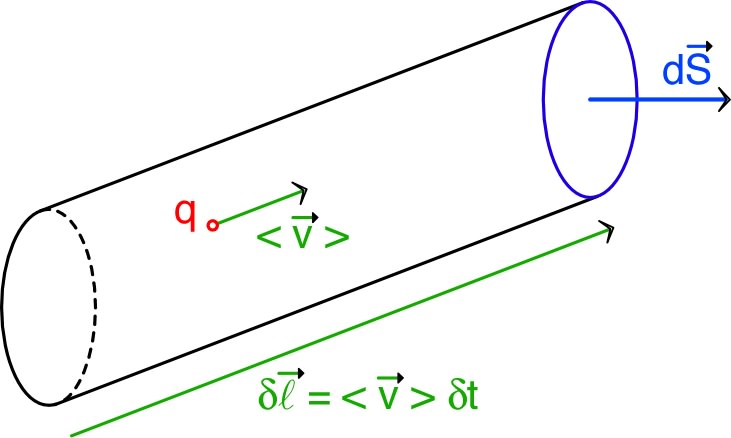
elCinLoc_Im/elCinLoc_Im2.jpg

En intégrant sur une surface SS, la charge δQδQ qui traverse pendant un intervalle δtδt est donc :  δQ=∬SdQ=∬j→∙dS→δtδQ=∬_S \:dQ=∬ \:\overset{→}{j}∙d\overset{→}{S} \: δt .

Le courant est alors :  I=δQδt=∬j→∙dS→I=\frac{δQ}{δt}=∬ \:\overset{→}{j}∙d\overset{→}{S}  (flux de la densité de courant).

• Dans le cas plus général où il y a plusieurs sortes de porteurs de charge (solution ionique par exemple), en notant  qiq_i  la charge des porteurs de type  ii  et  ρiρ_i  leur charge volumique, alors on peut exprimer le vecteur densité de courant par la relation :  j→=∑i(ρi⟨vi→⟩)\overset{→}{j}=∑_i \left(ρ_i \:\left⟨\overset{→}{v_i} \right⟩\right) .

Cette définition ne peut se faire autrement qu'en distinguant les contributions des différentes charges, car (entre autres) les charges + et -, qui ont des densités volumiques ρiρ_i de signes contraires, ont aussi des vitesses moyennes ⟨vi→⟩\left⟨\overset{→}{v_i} \right⟩ de sens contraires, donc des contributions de même sens à la densité de courant.

En outre, s'il y a plusieurs sortes de porteurs de charge de masses différentes, leurs vitesses moyennes sont différentes et contribuent différemment à la densité de courant, même si leurs charges sont égales.

◊ remarque : on peut visualiser l'écoulement local du courant à l'aide de “lignes de courant” (ligne en tout point tangente au vecteur j→\overset{→}{j} ) ; on peut également considérer des “tubes de courant” (tube délimité par l'ensemble des lignes de courant passant par le contour d'une surface SS donnée) :

elCinLoc_Im/elCinLoc_Im3.jpg

◊ remarque : les équations cartésiennes des lignes de courant peuvent être obtenues en intégrant les équations différentielles :  dxjx=dyjy=dzjz\frac{dx}{j_x} =\frac{dy}{j_y} =\frac{dz}{j_z}   (d'après le parallélisme entre j→\overset{→}{j} et un déplacement dOM⟶d\overset{⟶}{OM} le long d'une telle ligne).

◊ remarque : pour des charges électriques réparties en surface, on peut aussi définir une densité surfacique de courant à partir des charges surfaciques σiσ_i ; on pose alors :  js→=∑i(σi⟨vi→⟩)\overset{→}{j_s}=∑_i \left(σ_i \:\left⟨\overset{→}{v_i}\right⟩\right) .

1.2. Conservation de la charge électrique

• La charge électrique totale est une quantité exactement conservée (contrairement à la masse, qui n'est conservée que dans l'approximation non relativiste). Par suite, la charge QQ contenue dans un volume VV, délimité par une surface fermée SS, vérifie la relation :  −dQdt=Isortant=∬Sj→∙dS→-\frac{dQ}{dt}=I_{sortant}=∬_S \:\overset{→}{j}∙d\overset{→}{S} .

• Pour la surface fermée entourant le volume entre deux sections S1S_1 et S2S_2 d'un conducteur en régime permanent : dQdt=0\frac{dQ}{dt}=0 .  Ainsi le courant doit être le même au travers des deux sections :  Isortant=I2−I1=0I_{sortant}=I_2-I_1=0 .

elCinLoc_Im/elCinLoc_Im4.jpg

En particulier, pour un fil conducteur de diamètre variable, la densité de courant en régime permanent doit donc être plus grande dans les zones où le diamètre est plus petit. Ainsi, dans la mesure où la densité volumique des porteurs de charge est uniforme, il y en a plus dans la section plus grande donc ils se déplacent en moyenne moins vite.

• En pratique, toute accumulation de charges crée un champ électrique qui provoque l'évacuation du surplus de charges. Dans les conditions usuelles, “l'équilibre dynamique“ correspondant au régime permanent est atteint très rapidement (≈10−9s≈{10}^{-9} \:\mathrm{s}  dans un conducteur métallique ; ≈10−3s≈{10}^{-3} \:\mathrm{s}  dans une solution ionique).

Dans les conditions quasi-stationnaires, il ne peut s'accumuler des charges qu'en surface ou dans les zones où la conductivité varie (milieu inhomogène).


2. Conduction du courant

2.1. Conductivité et résistivité : loi d'Ohm locale

◊ remarque : pour simplifier, on considère dans ce qui suit des conducteurs métalliques où les seuls porteurs de charge sont des électrons ; les raisonnements sont aisément généralisables aux ions dans les électrolytes.

• Dans un milieu conducteur, les porteurs de charge sont soumis à un champ électrique “local”, somme du champ électrique imposé par l'extérieur et des champs exercés par les autres particules présentes dans le milieu.

On considère ici le champ électrique total moyen : on “élimine” les fluctuations microscopiques des effets “internes” par moyenne “locale” (dans chaque volume infinitésimal), sans se préoccuper de la façon dont ce champ s'établit sous l'effet des actions extérieures.

• Sous l'effet d'un champ électrique E→\overset{→}{E}, les porteurs de charge sont accélérés, mais ils subissent des chocs aléatoires qui tendent à leur redonner “périodiquement” une vitesse aléatoire, ce qui “annule” en moyenne la vitesse qui leur avait été donnée par l'accélération.

L'effet global est analogue à l'effet d'un frottement : il s'établit (très rapidement) une vitesse moyenne limite ⟨v→⟩\left⟨\overset{→}{v}\right⟩ proportionnelle à E→\overset{→}{E}, donc une densité de courant proportionnelle au champ :  j→=γE→\overset{→}{j}=γ \:\overset{→}{E}.  Cette proportionnalité constitue la loi d'Ohm locale ; le coefficient γγ est appelé “conductivité” (électrique).

• En considérant un porteur de charge de vitesse v0→\overset{→}{v_0} juste après un choc, alors sous l'effet de l'accélération :  v→≈v0→+qmE→t\overset{→}{v}≈\overset{→}{v_0}+\frac{q}{m} \overset{→}{E} \:t .  Donc, en moyenne sur l'intervalle entre deux chocs et sur l'ensemble des porteurs :  ⟨v→⟩≈⟨v0→⟩+qmE→⟨t⟩\left⟨\overset{→}{v}\right⟩≈\left⟨\overset{→}{v_0}\right⟩+\frac{q}{m} \overset{→}{E} \:\left⟨t\right⟩ .

Mais  ⟨v0→⟩=0→\left⟨\overset{→}{v_0}\right⟩=\overset{→}{0}  puisque les vitesses juste après un choc sont aléatoires, donc :  ⟨v→⟩≈qmE→⟨t⟩\left⟨\overset{→}{v}\right⟩≈\frac{q}{m} \overset{→}{E} \:\left⟨t\right⟩  avec  τ=⟨t⟩τ=\left⟨t\right⟩  (durée moyenne “entre deux chocs”, ≈10−14s≈{10}^{-14} \:\mathrm{s}  pour les électrons dans un métal dans les conditions usuelles).

La densité de courant peut alors s'écrire :  j→=∑i(ρi⟨vi→⟩)=γE→\overset{→}{j}=∑_i \left(ρ_i \:\left⟨\overset{→}{v_i} \right⟩\right) =γ\:\overset{→}{E}  avec la conductivité :  γ≈∑iρiqiτimiγ≈∑_i \frac{ρ_i \:q_i \:τ_i}{m_i} .

◊ remarque : puisque la vitesse croît progressivement pendant la durée entre deux chocs, la moyenne τ est un peu plus petite que le “temps moyen de collision”, mais il ne s'agit ici que d'une modélisation en première approximation.

◊ remarque : on raisonne avec un champ quasi uniforme et constant car les durées et distances entre deux chocs sont très petites ; on améliore ensuite éventuellement cette approximation en remplaçant la masse mim_i par une “masse effective”  mi*m_i^*  prenant en compte les effets moyens du milieu.

◊ remarque : on peut aussi écrire  ρi=niqiρ_i=n_i \:q_i  où nin_i est la concentration volumique de porteurs (nombre de particules par unité de volume) ; ceci correspond à :  γ≈∑iniqi2τimiγ≈∑_i \frac{n_i \:q_i^{\:2} \:τ_i}{m_i}  qui montre bien que les charges des deux signes contribuent constructivement au courant.

• Ces propriétés peuvent aussi s'écrire à l'aide de la “mobilité” μiμ_i des porteurs de charge, définie par :  ⟨vi→⟩=±μiE→\left⟨\overset{→}{v_i}\right⟩=± μ_i \:\overset{→}{E}  avec  μi=|qiτimi|μ_i=\left|\frac{q_i \:τ_i}{m_i} \right|  et  “±”=sgn(qi)\text{“±”}=\mathrm{sgn}\left(q_i \right)  pour décrire le sens.

La conductivité peut alors s'écrire :  γ≈∑i(|ρi|μi)γ≈∑_i \left(\left|ρ_i \right| \:μ_i \right)  (ceci est surtout utilisé en chimie pour la conductivité des électrolytes).

◊ remarque : on peut définir un coefficient de “résistivité”  ρ=1γρ=\frac{1}{γ}  mais il faut faire attention aux notations pour ne pas confondre avec la charge volumique.

2.2. Propriétés générales de la conductivité

• D'une façon générale, quand on élève la température d'un métal, la durée moyenne de collision ττ diminue d'autant que l'agitation thermique augmente ; par suite la conductivité diminue et la résistivité augmente.

Au contraire, quand on échauffe un “semi-conducteur”, les chocs de l'agitation thermique ralentissent les porteurs de charge mais ils en augmentent le nombre (des porteurs supplémentaires sont “libérés” sous l'effet des chocs) ; l'effet global est une augmentation de la conductivité et une diminution de la résistivité.

• À très basse température (≈5≈5  à  30K30 \:\mathrm{K}), la résistivité des métaux et de quelques autres composés devient nulle (conductivité infinie) ; c'est un effet quantique, appelé “supraconductivité”. Quand  T→0T→0 ,  le comportement des porteurs devient dans ce cas “collectif” et fait en moyenne “disparaître” l'effet des chocs thermiques.

• Les milieux ioniques (cristallisés, ou vitreux comme le silicate de sodium) sont isolants à basse température tant que les ions sont “figés” sous forme solide ; ils deviennent conducteurs quand la température devient suffisante pour que le milieu soit fluide.

2.3. Conductance et résistance; loi d'Ohm globale

• Un résistor (ou “conducteur ohmique”) est un dipôle électrocinétique (c'est-à-dire avec deux bornes de branchement) vérifiant la loi d'Ohm.

• Dans un tel dipôle, le courant est proportionnel à la tension UABU_{AB} appliquée entre les deux bornes du dipôle :  I=GUABI=G \:U_{AB}  où le coefficient de proportionnalité GG est appelé “conductance” du dipôle.

En effet, soient AA et BB les deux bornes de branchement, la tension appliquée au dipôle correspond à la “circulation” du champ électrique entre AA et BB :  UAB=VA−VB=−∫ABdV=−∫AB∇→V∙d𝓁→=∫ABE→∙d𝓁→U_{AB}=V_A-V_B=-∫_A^B \:dV=-∫_A^B \:\overset{→}{∇}V∙d\overset{→}{𝓁}=∫_A^B \:\overset{→}{E}∙d\overset{→}{𝓁} .

D'après la loi d'Ohm locale :  UAB=∫ABj→γ∙d𝓁→U_{AB}=∫_A^B \:\frac{\overset{→}{j}}{γ}∙d\overset{→}{𝓁} ,  donc si on intègre le long d'une ligne (ou d'un tube) de courant :  UAB=∫ABjγd𝓁U_{AB}=∫_A^B \:\frac{j}{γ} \:d𝓁 .

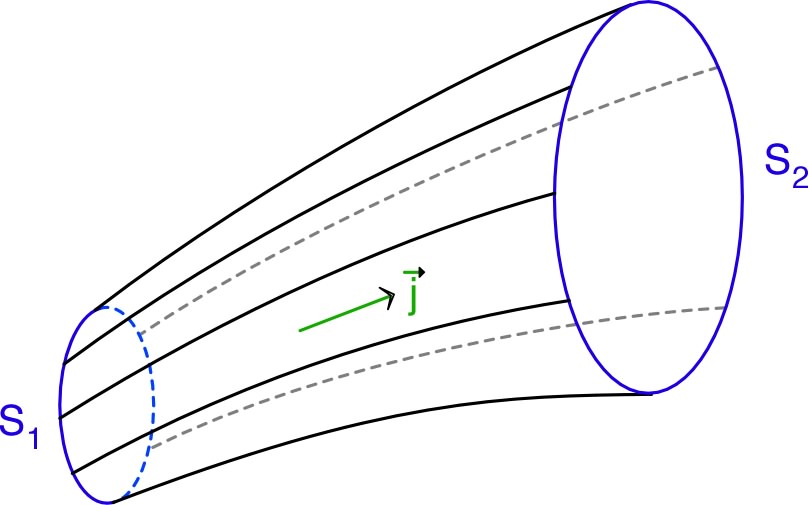
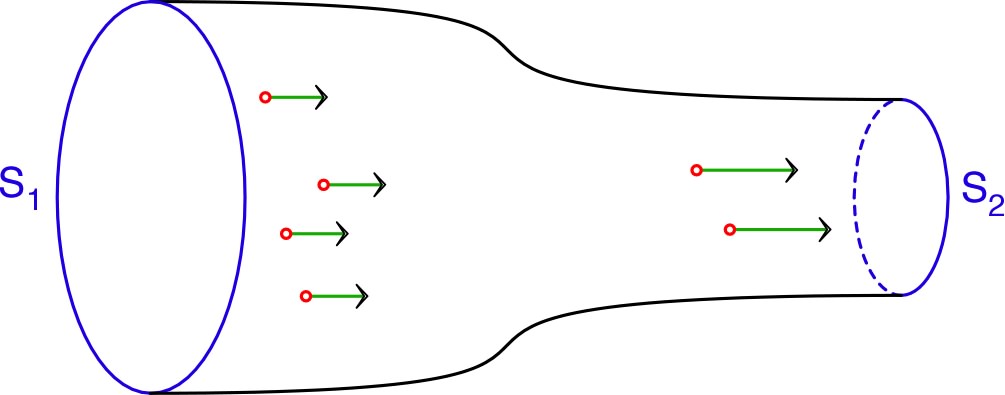
On peut alors considérer un tube de courant infinitésimal, de section δSδS dépendant de 𝓁𝓁 (le long du tube de courant infinitésimal), perpendiculaire au courant, donc sur une surface équipotentielle (car 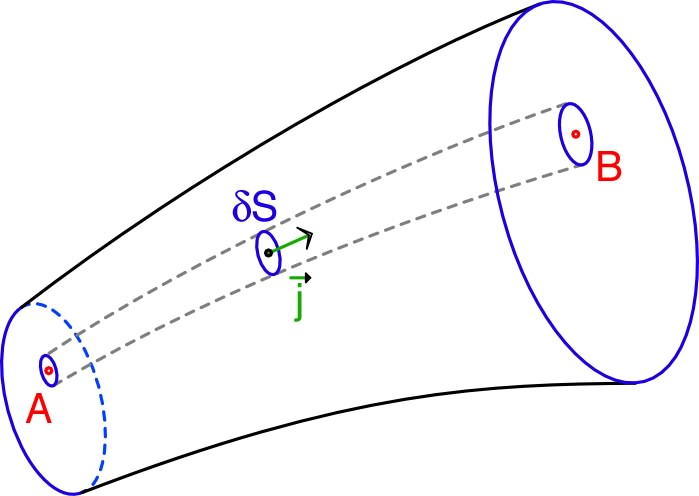j→∥E→\overset{→}{j} ∥ \overset{→}{E}) ; ainsi :  j=δIδSj=\frac{δI}{δS} . elCinLoc_Im/elCinLoc_Im5.jpg

Par suite :  UAB=δI∫ABd𝓁γδSU_{AB}=δI \;∫_A^B \,\frac{d𝓁}{γ \:δS} ,  c'est-à-dire que le courant dans le “tube” est proportionnel à la tension UABU_{AB} :  δI=δGUABδI=δG \;U_{AB}  avec un coefficient de proportionnalité :  δG=1∫ABd𝓁γδSδG=\frac{1}{∫_A^B \,\frac{d𝓁}{γ \:δS}} .

Mais puisque ceci est vrai pour tout tube de courant, c'est aussi vrai pour l'ensemble :  I=∫δI=GUABI=∫ δI=G \;U_{AB}  avec une conductance  G=∫δGG=∫ δG .

◊ remarque : ceci peut s'écrire  UAB=RIU_{AB}=R \:I  avec une résistance  R=1GR=\frac{1}{G} .

2.4. Exemple de calcul de conductance et de résistance

• Les expressions précédentes de GG et RR ne sont pas évidentes dans le cas général, mais elles sont simples dans les cas particuliers où les symétries simplifient les calculs.

• Par exemple, pour une portion de conducteur cylindrique homogène, assez long pour qu'on puisse supposer l'invariance par translation le long de l'axe, on peut supposer que la densité de courant est uniformément répartie sur la section (ce qui est plausible pour un conducteur homogène). Ceci correspond, compte tenu de la loi d'Ohm locale, à un champ E→\overset{→}{E} uniforme.

elCinLoc_Im/elCinLoc_Im6.jpg

Il est alors possible de faire un raisonnement simplifié adapté aux symétries du problème :  UAB=∫ABE→∙d𝓁→=ElU_{AB}=∫_A^B \;\overset{→}{E}∙d\overset{→}{𝓁} =E \:l  et  I=∫j→∙dS→=jSI=∫ \;\overset{→}{j}∙d\overset{→}{S} =j \:S  ;  mais  j=γEj=γ \:E  donc :  I=γES=γS𝓁UABI=γ \:E \:S=\frac{γ \:S}{𝓁} \:U_{AB}  c'est-à-dire  G=γS𝓁G=\frac{γ \:S}{𝓁}  et  R=𝓁γSR=\frac{𝓁}{γ \:S} .

◊ remarque : l'hypothèse d'une répartition uniforme de la densité de courant sur la section, dans le cas d'un conducteur homogène, n'est pas si évidente qu'on pourrait le croire; elle est correcte en courant continu, mais elle devient fausse en courant alternatif de haute fréquence : le courant circule alors préférentiellement à proximité de la surface (“effet de peau”).

• Pour un conducteur en forme de cylindre creux, auquel on applique une tension UABU_{AB} entre ses surfaces latérales interne et externe, le calcul est analogue (bien que moins simple). 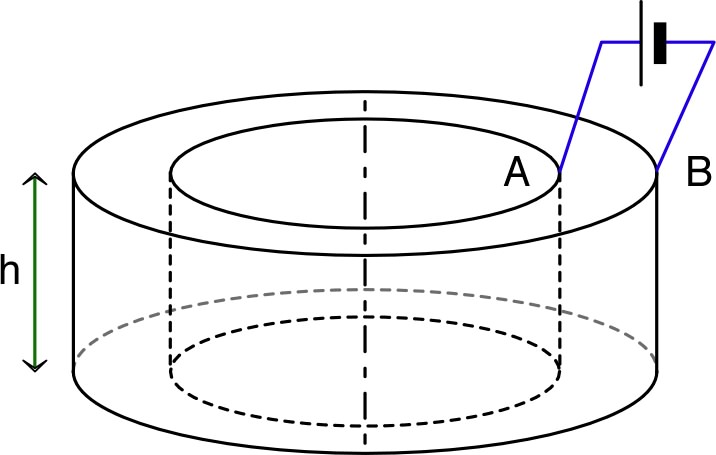elCinLoc_Im/elCinLoc_Im7.jpg

D'après les symétries, on peut raisonnablement supposer que la densité de courant est radiale et ne dépend que de rr : uniformément répartie par rapport à l'angle θθ et l'altitude zz (ce qui est plausible pour un conducteur homogène). Ceci correspond, compte tenu de la loi d'Ohm locale, à un champ E→\overset{→}{E} radial dont la coordonnée radiale ErE_r ne dépend que de rr.

Le raisonnement simplifié adapté aux symétries du problème donne alors :  UAB=∫rArBEr(r)drU_{AB}=∫_{r_A}^{r_B} \;E_r \left(r\right) \:dr  et  I=∫j→∙dS→=2πrhj(r)I=∫ \:\overset{→}{j}∙d\overset{→}{S} =2π \:r \:h \:j\left(r\right)  quel que soit rr (d'après la conservation de la charge). Finalement :  Er(r)=j(r)γ=Iγ2πrhE_r \left(r\right)=\frac{j\left(r\right)}{γ}=\frac{I}{γ \:2π \:r \:h}  et  UAB=RIU_{AB}=R \:I  avec  R=1γ2πhln(rBrA)R=\frac{1}{γ \:2π\: h} \:\ln\left({\frac{r_B}{r_A}}\right) .

◊ remarque : l'argument d'invariance de II en fonction de rr donne un champ en 1r\frac{1}{r} comme ce qui serait déduit du théorème de Gauss en supposant une charge surfacique uniforme sur les faces AA et BB, mais ce n'en est pas une conséquence (le régime permanent en milieu homogène indique que la charge volumique est nulle, mais la répartition des charges en surface des conducteurs découle des symétries).

📖 exercices n° I et II.


3. Aspects énergétiques; loi de Ioule

• Lorsque les actions extérieures causent dans le conducteur un champ électrique E→\overset{→}{E}, celui-ci fournit du travail aux porteurs de charge pendant la durée de l'accélération (entre deux chocs) :  dwi=Fi→∙dOMi⟶=qiE→∙vi→dtdw_i=\overset{→}{F_i}∙d\overset{⟶}{OM_i}=q_i \overset{→}{E}∙\overset{→}{v_i} \:dt  ;  mais après chaque choc les vitesses sont à nouveau aléatoires, donc ce travail provenant des actions extérieures est transmis au conducteur.

En moyenne sur l'ensemble des porteurs de charge dans un volume δ𝒱δ𝒱 :  dW=∑(ρiE→∙⟨vi→⟩)dtδ𝒱=j→∙E→dtδ𝒱dW=∑ \left(ρ_i \:\overset{→}{E}∙\left⟨\overset{→}{v_i} \right⟩\right) \:dt \:δ𝒱=\overset{→}{j}∙\overset{→}{E} \:dt \:δ𝒱 .  La puissance reçue par δ𝒱δ𝒱 est donc :  δ𝒫=dWdt=j→∙E→δ𝒱δ𝒫=\frac{dW}{dt}=\overset{→}{j}∙\overset{→}{E} \;δ𝒱 .

Ceci correspond à une densité volumique de puissance :  p=δ𝒫δ𝒱=j→∙E→=γE2=j2γp=\frac{δ𝒫}{δ𝒱}=\overset{→}{j}∙\overset{→}{E}=γ \:E^2=\frac{j^2}{γ}  (effet Joule).

• Intégrée sur l'ensemble du volume d'un conducteur ohmique, cette densité de puissance donne la puissance Joule :  𝒫=∫j→∙E→d𝒱=∫j→∙dS→∫E→∙d𝓁→𝒫=∫ \:\overset{→}{j}∙\overset{→}{E} \:d𝒱=∫ \:\overset{→}{j}∙d\overset{→}{S} \;\;∫ \:\overset{→}{E}∙d\overset{→}{𝓁}  avec d𝓁→d\overset{→}{𝓁} le long d'une ligne de courant et dS→d\overset{→}{S} sur une section équipotentielle du conducteur ; par suite :  𝒫=UABI=GUAB2=RI2𝒫=U_{AB} \:I=G \:\:U_{AB}^{\:2}=R \:I^2 .

◊ remarque : pour un dipôle quelconque (en régime permanent), il faut tenir compte des f.e.m. et f.c.e.m. et le calcul “local” est en général compliqué.

📖 exercice n° III.