ÉLECTROCINÉTIQUE - LOIS LOCALES

ÉLECTROCINÉTIQUE - LOIS LOCALES - exercices

I. Résistance d'une prise de terre

1. • Deux sphères métalliques concentriques, de rayons

R_1

R_2>R_1

, supposées parfaitement conductrices (on néglige leur résistance en comparaison des autres résistances qui interviennent dans le problème), sont séparées par un milieu peu conducteur de résistivité

ρ=\frac{1}{γ}

. Calculer la résistance entre les deux sphères.

2. • Que devient l'expression précédente quand

R_2→∞

(

R_2≫R_1

) ?

Données :

R_1=10 \:\mathrm{cm}

;

ρ=103 \:\mathrm{Ω.m}

(sol argileux).

II. Conduction non ohmique ; diode en charge d'espace

• Une cathode plane

C

émet (par effet thermoélectronique) des électrons qui sont attirés par une anode plane

A

, parallèle à la cathode. L'ensemble est placé dans une ampoule à vide.
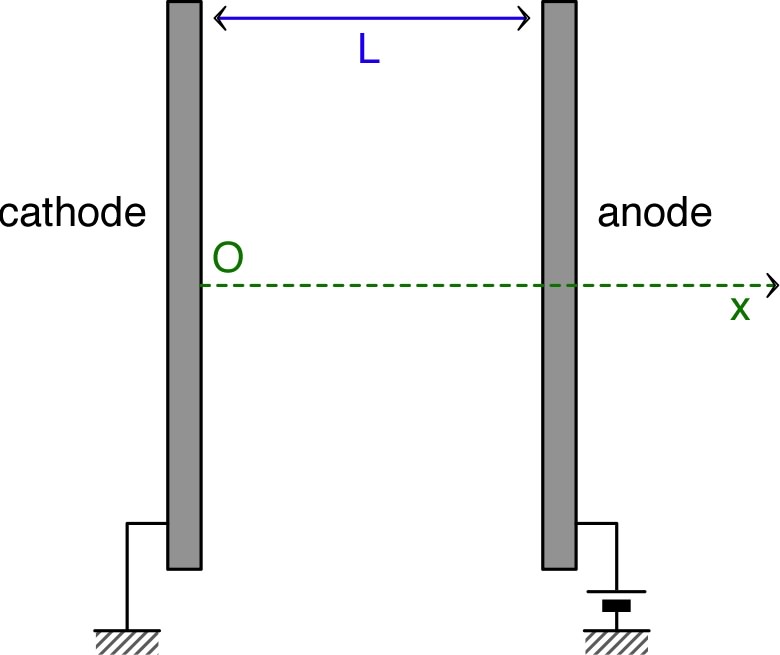
• Le plan de la cathode est choisi comme origine des abscisses (

x=0

) et son potentiel est choisi comme référence (

V=0

). Le plan de l'anode est à l'abscisse

x=L

et son potentiel est maintenu à la valeur positive

V=V_a

.
• Le système est considéré comme pratiquement infini dans les directions perpendiculaires à l'axe

Ox

(les différentes grandeurs qui interviennent dans le problème ne peuvent donc dépendre que de

x

).
• Un régime permanent s'établit pour le mouvement des électrons et un courant constant circule entre les électrodes. On admet que les électrons sont émis par la cathode avec une vitesse négligeable et que le champ électrique est nul sur la cathode.

1. a) Écrire la relation que fournit la mécanique newtonienne entre la vitesse

u\left(x\right)

des électrons et le potentiel

V\left(x\right)

.
b) Écrire la relation de définition de la densité de courant

j

(algébrique) en fonction de la vitesse

u\left(x\right)

des électrons et de leur “concentration”, ou densité volumique,

n\left(x\right)

.
c) Écrire l'équation différentielle qui relie

V\left(x\right)

n\left(x\right)

.

2. • Déduire de ces résultats l'équation différentielle qui détermine

V\left(x\right)

.

3. • Intégrer cette équation et donner l'expression du courant

I

relatif à une portion de surface

S

de la cathode.
◊ indication : l'expression est de la forme :

I=K \:V_a^{\;α}

(valable bien sûr uniquement si le courant de saturation n'est pas atteint).

4. • Quelle serait la résistivité d'un corps de section

S

et de longueur

L

parcouru par le même courant, pour

V_a

fixé ? Que peut-on en conclure ?

Données :	$L=8 \:\mathrm{cm}$ ; $S=1 \:\mathrm{cm^2}$ ; $\frac{1}{4π \:ε_0}=9.10^9 \:\mathrm{m.F^{-1}}$ ; $V_a=100 \:\mathrm{V}$ ;
	$q_e=-1,6.{10}^{-19} \:\mathrm{C}$ ; $m_e=0,91.{10}^{-30} \:\mathrm{kg}$ .

III. Interprétation de l'effet Joule

• On considère le modèle de conduction électrique métallique défini par les hypothèses suivantes :

◊	la conduction est assurée par des électrons mobiles, de masse $m$ , de charge $-e$ , dont le nombre par unité de volume (densité volumique) est $n$ ;
◊	ces électrons subissent des chocs aléatoires dans le réseau cristallin, chaque électron ayant une probabilité différentielle : $dP=\frac{dt}{τ}$ (où $τ$ est une constante) de subir un choc pendant l'intervalle de temps $dt$ , indépendamment des chocs antérieurs ;
◊	les chocs “désorientent” complètement les vitesses des électrons : la distribution statistique de la vitesse $\overset{→}{v_0}$ juste après un choc est totalement aléatoire (c'est-à-dire exactement la même distribution, liée à l'agitation thermique, que s'il n'y avait aucun effet de courant électrique) ;
◊	entre deux chocs, le mouvement d'un électron est celui d'une particule “libre” (soumise uniquement à l'effet du champ électrique imposé dans le conducteur).

1. a) Quelle est la probabilité pour qu'un électron ne subisse pas de choc entre

t

t+dt

?
b) Soit

π\left(t\right)

la probabilité pour qu'un électron ne subisse pas de choc entre l'instant initial (

t=0

) et un instant

t

ultérieur, relier simplement

π\left(t+dt\right)

π\left(t\right)

.
c) En intégrant l'équation différentielle ainsi obtenue, en déduire que :

π\left(t\right)=\mathrm{e}^{-t/τ}

.

2. • En déduire l'expression de la durée moyenne de l'intervalle de temps

t_1

séparant deux chocs, en prenant comme origine du temps pour

π\left(t\right)

l'instant d'un choc.

3. • On considère que les électrons “libres” du métal sont soumis à un champ électrique moyen

\overset{→}{E}

uniforme et constant.
a) Exprimer la valeur moyenne de leur vitesse à un instant quelconque.
☞ indication : on peut remarquer qu'à chaque instant la vitesse d'un électron est la somme de la vitesse initiale aléatoire

\overset{→}{v_0}

et de la “vitesse acquise” sous l'effet du champ électrique.
b) En déduire la densité de courant

\overset{→}{j}

qui apparaît, en régime permanent, au sein du métal.
c) En déduire l'expression de la conductivité

γ

de ce métal.

4. • L'accroissement d'énergie cinétique

∆ℰ_c

dû au champ

\overset{→}{E}

entre deux chocs successifs est dissipé sous forme d'agitation thermique (vibrations du réseau cristallin) lors des chocs ultérieurs.
a) Exprimer la valeur moyenne

\left⟨∆ℰ_c \right⟩

en fonction de

e

m

τ

E

.
b) En déduire l'expression de la densité volumique de puissance dissipée, notée

p

, en fonction de

γ

E

.

5. • Exprimer puis calculer

\left‖\left⟨ \overset{→}{v} \right⟩\right‖

\left⟨ \overset{→}{v_0} \right⟩

.
• Pour l'application numérique : on considère un fil de cuivre, de section

s={10}^{-6} \:\mathrm{m^2}

, parcouru par un courant

I=2 \:\mathrm{A}

Données :

e = \left|q_e\right| = 1,6.{10}^{-19} \:\mathrm{C}

;

m_e = 9,1.{10}^{-31} \:\mathrm{kg}

;

𝒩_A = 6,02.{10}^{23}

;

constantes physiques du cuivre :

	conductivité : $γ=6.{10}^7 \:\mathrm{Ω^{-1}.m^{-1}}$ ; masse volumique : $μ=8900 \:\mathrm{kg.m^{-3}}$ ;
	masse molaire : $M=63,6 \:\mathrm{g.mol^{-1}}$ ;
	nombre d'électrons mobiles par atome de cuivre : $≈1$ ;
	libre parcours moyen des électrons mobiles : $\left⟨𝓁\right⟩=4,5.{10}^{-8} \:\mathrm{m}$ .