E.C.III - ÉLECTROCINÉTIQUE

E.C.III - ÉLECTROCINÉTIQUE - RÉSEAUX

1. Principe de superposition (théorème d'Helmholtz)

• Pour un réseau dont les dipôles ont des caractéristiques affines, les équations décrivant le circuit sont linéaires :

∑_j \left(R_{ij} \:I_{ij} \right)=∑_j E_{ij}

où les coefficients

R_{ij}

sont des résistances, où les

E_{ij}

sont des forces électromotrices (f.e.m.) et où on somme sur les branches

j

constituant la maille

i

Pour de tels systèmes d’équations (linéaires), les courants et tensions causés par plusieurs générateurs sont les sommes des courants et tensions causés respectivement par chacun des générateurs (vrais ou modélisés).

☞ remarque : ceci suppose toutefois que les f.e.m. ont des valeurs “fixées” ; on ne peut pas généraliser aux dipôles “commandés” (dont la caractéristique dépend des tensions et/ou courants dans le circuit).

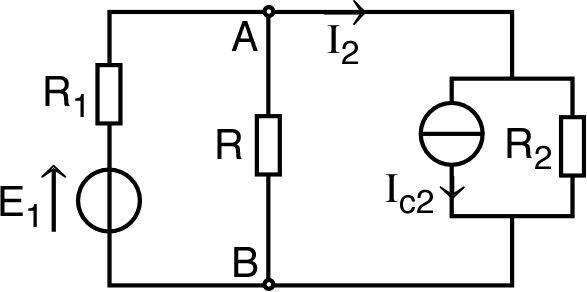
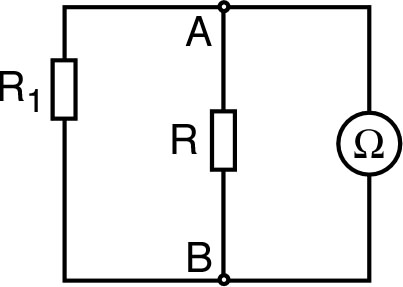
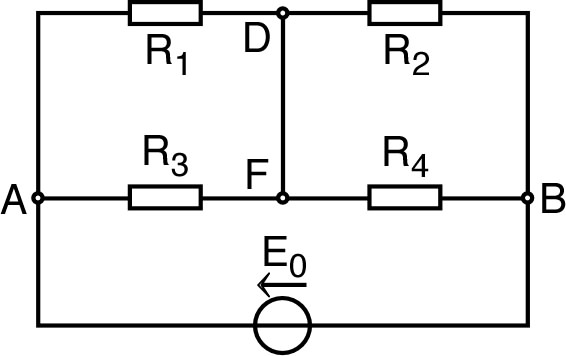
• On peut considérer par exemple le calcul du courant

I_2

, puis de la tension

U_{AB}

, dans le montage ci-contre.

• Le courant causé par le générateur

E_1

est :

I_{2_{(1)}}=\frac{R \:E_1}{R_1 \:R_2+(R_1+R_2 ) \:R}

; le courant causé par le générateur

I_{c2}

est :

I_{2_{(2)}}=\frac{(R+R_1) \:R_2 \:I_{c2}}{R_1 \,R_2+(R_1+R_2 ) \:R}

Le courant total cherché est donc :

I_2=I_{2_{(1)}}+I_{2_{(2)}}=\frac{R \:E_1+(R+R_1 ) \:R_2 \:I_{c2}}{R_1 \,R_2+(R_1+R_2 ) \:R}

.

• Le principe de superposition s’applique aussi pour les tensions :

	$U_{{AB}_{(1)}}=R_2 \:I_{2_{(1)}}=\frac{R \,R_2 \,E_1}{R_1 \,R_2+(R_1+R_2 ) \:R}$ ;
	$U_{{AB}_{(2)}}=R_2 .\left(I_{2_{(2)}}-I_{c2} \right)=-\frac{R \:R_1 \:R_2 \:I_{c2}}{R_1 \:R_2+(R_1+R_2 ) \:R}$ ;

donc au total :

U_{AB}=U_{{AB}_{(1)}}+U_{{AB}_{(2)}}=R \:R_2 \:\frac{E_1- R_1 \:I_{c2}}{R_1 \,R_2+(R_1+R_2 ) \:R}

(résultat de la loi de Millman).

📖 exercice n° I.

2. Théorème de Thévenin

• Si on ne s'intéresse qu'à l'une des branches, le calcul peut être simplifié.

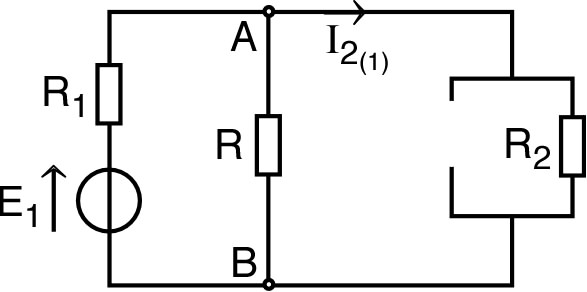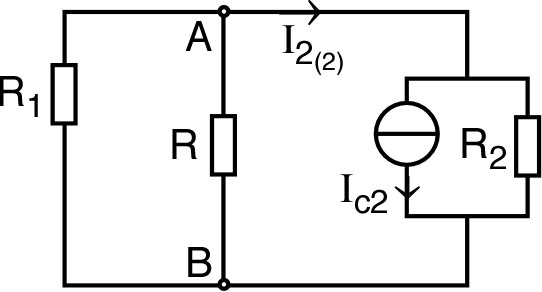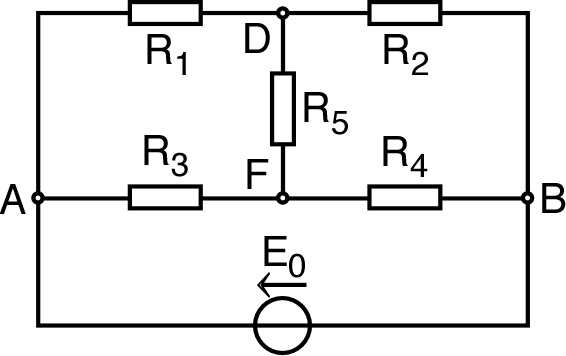
D’après la linéarité des équations (caractéristiques affines), toute partie du réseau entre deux nœuds

A

B

donnés possède une caractéristique affine ; elle peut donc être représentée symboliquement par un générateur de Thévenin équivalent (théorème de Thévenin).

• Dans l'exemple étudié précédemment, la partie gauche du montage a une f.e.m. correspondant à sa tension “à vide” :

E_{eq}=U_{{AB}_{(0)}}=E_1 \,\frac{R}{R+R_1}

et une résistance (générateur “arrêté”) :

R_{eq}=\frac{R \:R_1}{R+R_1}

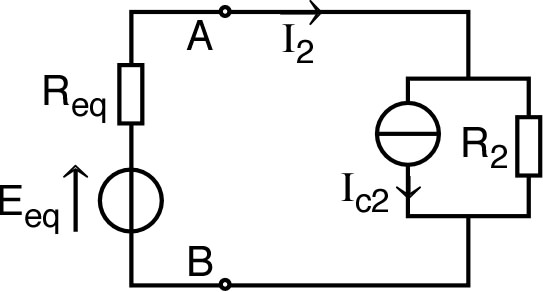
Il suffit alors d'en déduire le courant cherché par la loi de Pouillet :

I_2=\frac{E_{eq}- R_2 \:I_{c2}}{R_{eq}+R_2}=\frac{E_1 \:R- R_2 \:I_{c2}.(R+R_1 )}{R_1 \:R_2+(R_1+R_2 ) \:R}

• On peut chercher par cette méthode la condition d'équilibre d'un pont de Wheatstone, en considérant le courant dans la branche

DF

(

I_5=0

) :


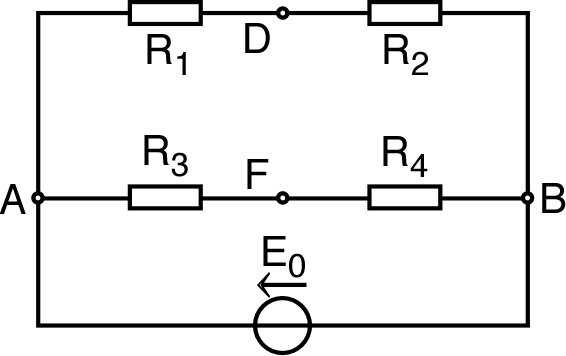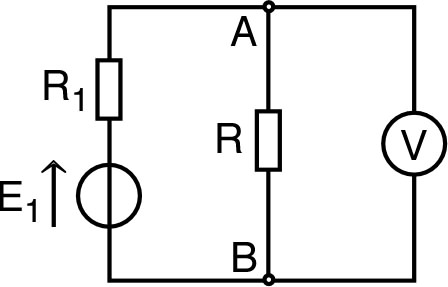
	(circuit “à vide”)

La f.e.m. (tension

U_{DF}

“à vide”, en l'absence de

R_5

) peut se calculer par la méthode du pont diviseur de tension :

	$U_{AD}=E_0 \,\frac{R_1}{R_1+R_2}$ et $U_{AF}=E_0 \,\frac{R_3}{R_3+R_4}$ ;
	$E_{eq}=U_{DF}=U_{AF}-U_{AD}=E_0 \,\frac{R_2 \,R_3-R_1 \,R_4}{(R_1+R_2 )(R_3+R_4 )}$ .

La résistance équivalente entre

D

F

(générateur à l'arrêt) est :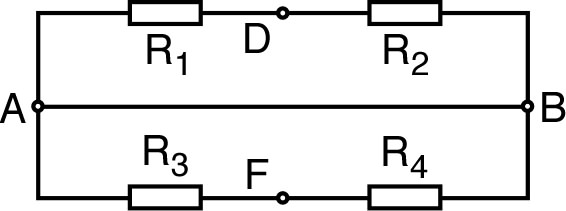

R_{eq}=\frac{R_1 \:R_2}{R_1+R_2}+\frac{R_3 \:R_4}{R_3+R_4}

• Si on cherche surtout “l’équilibre du pont”, défini par l’une ou l’autre des conditions :

I_5=\frac{E_{eq}}{R_{eq}+R_5}=0

U_{DF}=R_5 \:I_5=0

, on obtient :

E_{eq}=0

, donc :

R_1 \:R_4=R_2 \:R_3

3. Théorème de Norton

• De même, pour un montage dont tous les dipôles ont des caractéristiques affines, toute partie du réseau entre deux nœuds

A

B

donnés possède aussi une caractéristique affine ; elle peut donc aussi être représentée symboliquement par un générateur de Norton équivalent (théorème de Norton).

En particulier, pour l’assemblage de deux générateurs en parallèle : les courants de court-circuit s’ajoutent et les conductances s’ajoutent.

◊ remarque : d'après l’équivalence des représentations de Thévenin et Norton (

U=E-R \:I

équivaut à

I=I_c-G \:U

avec

I_c=\frac{E}{R}

G=\frac{1}{R}

), le théorème de Norton n’est qu’une autre façon d’exprimer le théorème de Thévenin.

• On peut chercher ainsi la condition d'équilibre du pont de Wheatstone envisagé précédemment.

Le courant de court-circuit (en court-circuitant

R_5

) peut se calculer à partir de la loi de Pouillet et de la méthode du “pont diviseur de courant” :


	(circuit “à vide”)

I_0=\frac{E_0}{R_{13}+R_{24}}

avec

R_{13}=\frac{R_1 \:R_3}{R_1+R_3}

R_{24}=\frac{R_2 \:R_4}{R_2+R_4}

;

I_1=I_0 \,\frac{R_3}{R_1+R_3}

I_2=I_0 \:\frac{R_4}{R_2+R_4}

;

I_{c_{eq}}=I_{DF}=I_1-I_2=E_0 \:\frac{R_2 \:R_3-R_1 \:R_4}{R_1 \:R_3.(R_2+R_4 )+R_2 \:R_4.(R_1+R_3 )}

Le calcul de la conductance équivalente (

G_{eq}=\frac{1}{R_{eq}}

) entre

D

F

est le même que pour la méthode de Thévenin.

• Si on cherche surtout “l’équilibre du pont”, défini par l’une ou l’autre des conditions :

U_{DF}=\frac{I_{c_{eq}}}{G_{eq}+G_5}=0

I_5=G_5 \:U_{DF}=0

, on obtient :

I_{c_{eq }}=0

, donc ici encore :

R_1 \:R_4=R_2 \:R_3

.

📖 exercices n° II et III.